The Open University Maths Dept University of Oxford

The Open University Maths Dept University of Oxford Dept of Education Learner Generated Examples in the Teaching of Mathematics John Mason Grahamstown May 2009 1

Another & Another Write down a pair of numbers whose difference is 2 / and another pair / Write down a pair which obscure the difference of 2 as much as possible 2 What did you notice?

Decimal Construction 1 Write down a decimal number between 2 and 3 but which does not use the digit 5 and which does use the digit 7 and which is as close to 5/2 as possible / 3

More Or Less Rectangles & Area Draw a rectilinear figure which requires at least 4 rectangles in any decomposition area No. of rectangles more same fewer 4 more same less more rects more area more rects same area more rects less area same rects more area same rects less area fewer rects more area fewer rects same area less area How many can have the same perimeter?

More Or Less Percent & Value 50% of something is 20 Value % of 5 more same less more 60% of 60 is 36 60% of 30 is 20 40% of 30 is 12 same 50% of 60 is 30 50% of 40 is 20 50% of 30 is 15 less 40% of 60 is 24 40% of 50 is 20 40% of 40 is 16

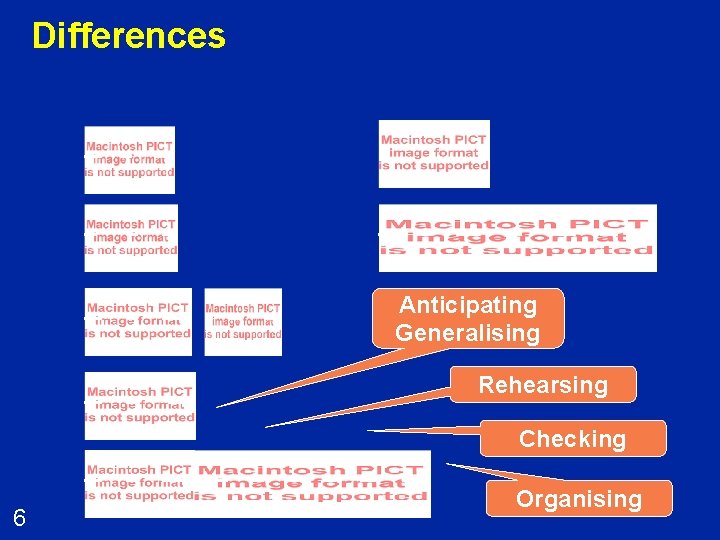
Differences Anticipating Generalising Rehearsing Checking 6 Organising

Decimal Construction 2 Write down a decimal number which has the property that every finite string of digits appears consecutively somewhere in the digits of your number / Write down a decimal number in which the string of digits for each whole number appears somewhere as a consecutive string in your number / 7

Fraction Construction Write down a fraction which uses all of the digits from 0 to 9 and which lies between 3 and 4 and which is as close to 10/3 as possible / 8

Extremes Write down a number which you think no-one else in the room is likely to write down / … which no-one is ever likely to have written down! / Write down a positive integer. The person writing down the smallest positive integer that no-one else writes down gets a prize! / 9

Interlude on Creativity often identified with person, or product / often associated with novelty / these divert attention from the essence of creativity: / a flow of a particular kind of energy / – Aha! Insight; construction; completion Issue: how to encourage its appearance , and how to exploit the energy when it arises / 10

Quadrilateral Construction 1 Draw a quadrilateral which has one pair of sides parallel, and one pair of sides equal, and one pair of angles equal How many different ones can you find? / 11

Quadrilateral Construction 2 Draw a quadrilateral which has one pair of opposite sides equal, and one pair of opposite sides perpendicular, and a second pair of sides equal / 12

Learner Choice The more choices I make, the more likely I am to be engaged / Choices of: / – special or particular cases, in order to comprehend – example (complexity, generality) – example meeting constraints – constraints to be met – distribution of activity / all contributing to – Sense of possible variation; generality; access to richer example spaces 13

Lined Up Write down the equations of two straight lines whose x-intercepts differ by 2 / and whose y-intercepts differ by 2 / and whose slopes differ by 2 / Now: find all such! / 14

Example Spaces /asking learners to construct objects – reveals something of their awareness of the scope of generality – promotes the extending and enriching of the examples available to them: their example spaces /The examples which come to mind are available in a given situation form an example space (Watson & Mason 2002) 15

Spinners /Colour the spinner so that the probability of getting a red is 1/4 and of a yellow is 3/8 /Colour the spinner so that a red is ¾ as likely as a yellow 16

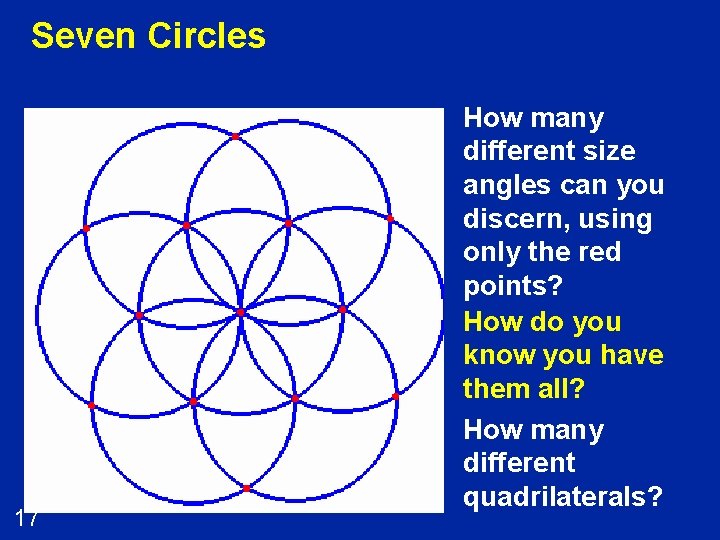
Seven Circles 17 How many different size angles can you discern, using only the red points? How do you know you have them all? How many different quadrilaterals?

Creativity as Energy Flow / moment of insight – requires preparation – entails perspiration and performance! / satisfaction of construction Feel creative when you go beyond habit/routine/expectation 18 Energy flow enables you to take initiative, to respond freshly, to feel good

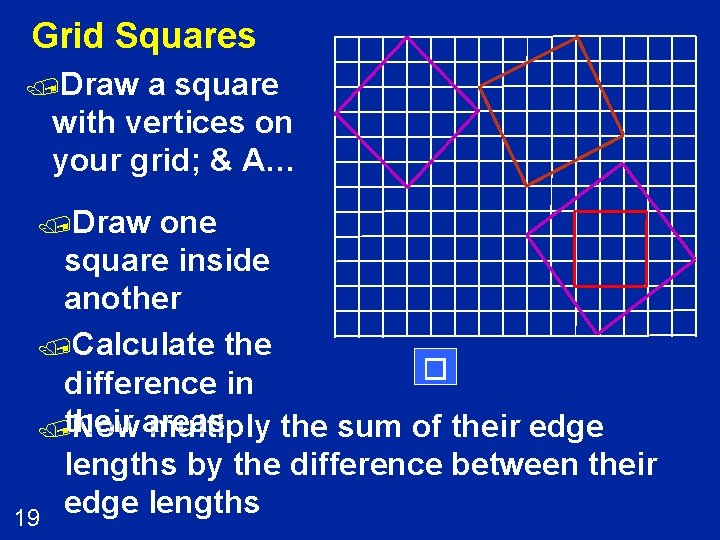
Grid Squares /Draw a square with vertices on your grid; & A… /Draw one square inside another /Calculate the � difference in /their Now areas multiply the sum of their edge lengths by the difference between their edge lengths 19

Powers /Am I getting students to make significant mathematical choices for themselves? /Am I stimulating learners to use their own powers, or am I abusing their powers by trying to do things for them? – – – 20 To imagine & to express To specialise & to generalise To conjecture & to convince To stress & to ignore To extend & to restrict

More Resources /Questions & Prompts for Mathematical Thinking (ATM Derby: primary & secondary versions) /Thinkers (ATM Derby) /Mathematics as a Constructive Activity (Erlbaum) /Designing & Using Mathematical Tasks (Tarquin) /http: //mcs. open. ac. uk/jhm 3 /j. h. mason @ open. ac. uk 21