The Ontology Spectrum Semantic Models Dr Leo Obrst

The Ontology Spectrum & Semantic Models • Dr. Leo Obrst • MITRE • Information Semantics Group • Information Discovery & Understanding • Center for Innovative Computing & Informatics • January 12 & 19, 2006 Copyright 2006, The MITRE Corporation

Abstract The Ontology Spectrum describes a range of semantic models of increasing expressiveness and complexity: taxonomy, thesaurus, conceptual model, and logical theory. This presentation initially describes the Ontology Spectrum and important distinctions related to semantic models, e. g. , the distinction among term, concept, and real world referent; the distinction among syntax, semantics, and pragmatics; the distinction between intension and extension; and de facto distinctions that the ISO 11179 standard makes (as do many others): data objects, classification objects, terminology objects, meaning objects, and the relationships among these. Then the individual semantic model types are discussed: weak and strong taxonomies, thesaurus, and weak and strong ontologies (conceptual model and logical theory, respectively). Each of these are defined, exemplified, and discussed with respect to when a more expressive model is needed. If time permits, semantic integration and interoperability are discussed with respect to the models. Finally, a pointer to an expansion of the logical theory portion of the Ontology Spectrum is given: the Logic Spectrum, which describes the range of less to more expressive logics used for ontology and knowledge representation. Copyright 2006, The MITRE Corporation 2

Agenda • Semantic Models: What & How to Decide? – Information Semantics – Tightness of Coupling & Semantic Explicitness – Ontology and Ontologies – The Ontology Spectrum – Preliminary Concepts – Taxonomies – Thesauri – Conceptual Models: Weak Ontologies – Logical Theories: Strong Ontologies – Semantic Integration, Mapping – What Do We Want the Future to Be? – More: Copyright 2006, The MITRE Corporation 3

Information Semantics • Provide semantic representation (meaning) for our systems, our data, our documents, our agents • Focus on machines more closely interacting at human conceptual level • Spans Ontologies, Knowledge Representation, Semantic Web, Semantics in NLP, Knowledge Management • Linking notion is Ontologies (rich formal models) • Content is King or should be! – And the better the content… Copyright 2006, The MITRE Corporation 4

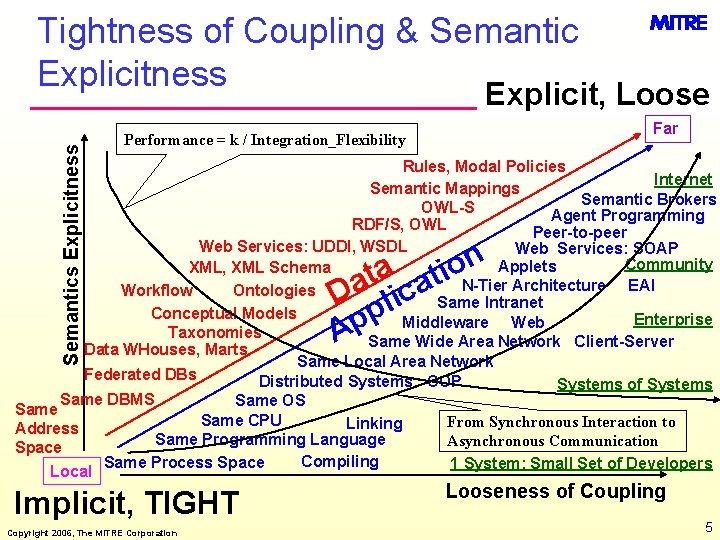
Tightness of Coupling & Semantic Explicitness Semantics Explicitness Explicit, Loose Far Performance = k / Integration_Flexibility Rules, Modal Policies Internet Semantic Mappings Semantic Brokers OWL-S Agent Programming RDF/S, OWL Peer-to-peer Web Services: UDDI, WSDL Web Services: SOAP Community Applets XML, XML Schema N-Tier Architecture EAI Workflow Ontologies Same Intranet Conceptual Models Enterprise Middleware Web Taxonomies Same Wide Area Network Client-Server Data WHouses, Marts Same Local Area Network Federated DBs Distributed Systems OOP Systems of Systems Same DBMS Same OS Same CPU From Synchronous Interaction to Linking Address Same Programming Language Asynchronous Communication Space Compiling Same Process Space 1 System: Small Set of Developers Local Implicit, TIGHT Copyright 2006, The MITRE Corporation n o ti ta a a D lic p p A Looseness of Coupling 5

Ontology & Ontologies 1 • An ontology defines the terms used to describe and represent an area of knowledge (subject matter) – An ontology also is the model (set of concepts) for the meaning of those terms – An ontology thus defines the vocabulary and the meaning of that vocabulary • Ontologies are used by people, databases, and applications that need to share domain information – Domain: a specific subject area or area of knowledge, like medicine, tool manufacturing, real estate, automobile repair, financial management, etc. • Ontologies include computer-usable definitions of basic concepts in the domain and the relationships among them – They encode domain knowledge (modular) – Knowledge that spans domains (composable) – Make knowledge available (reusable) Copyright 2006, The MITRE Corporation 6

Ontology & Ontologies 2 • The term ontology has been used to describe models with different degrees of structure (Ontology Spectrum) – Less structure: Taxonomies (Semio/Convera taxonomies, Yahoo hierarchy, biological taxonomy, UNSPSC), Database Schemas (many) and metadata schemes (ICML, eb. XML, WSDL) – More Structure: Thesauri (Word. Net, CALL, DTIC), Conceptual Models (OO models, UML) – Most Structure: Logical Theories (Ontolingua, TOVE, CYC, Semantic Web) • Ontologies are usually expressed in a logic-based language – Enabling detailed, sound, meaningful distinctions to be made among the classes, properties, & relations – More expressive meaning but maintain “computability” • Using ontologies, tomorrow's applications can be "intelligent” – Work at the human conceptual level • Ontologies are usually developed using special tools that can model rich semantics Copyright 2006, The MITRE Corporation 7

Ontology & Ontologies 3 • Ontologies are typically developed by a team with individuals of two types – Domain Experts: have the knowledge of a specfic domain – Modelers (ontologists): know how to formally model domains, spanning domains, semantic properties, relations • On-going research investigates semi-automation of ontology development – State-of-art for next 100 years will be semi-automation – Humans have rich semantic models & understanding, machines poor so far – Want our machines to interact more closely at human concept level – The more & richer the knowledge sources developed & used, the easier it gets (bootstrapping, learning) • Rigorous ontology development methodologies evolving (e. g. , Methontology), today’s practice is set of principles/processes • Tools are being developed that apply formal ontology analysis techniques to assist KR-naïve domain experts in building ontologies (Onto. Clean) Copyright 2006, The MITRE Corporation 8

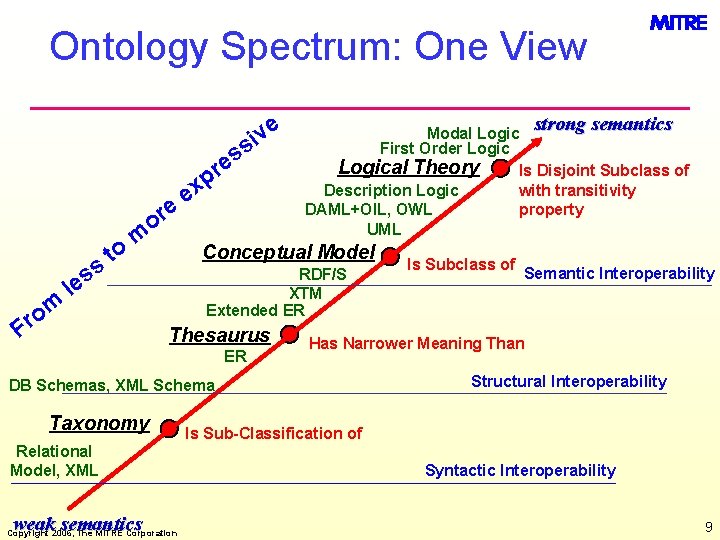
Ontology Spectrum: One View e iv s s e e or ss m o r to m e Conceptual Model RDF/S XTM Extended ER le F r p x strong semantics Modal Logic First Order Logical Theory Is Disjoint Subclass of with transitivity Description Logic DAML+OIL, OWL property UML Thesaurus ER Relational Model, XML weak semantics Copyright 2006, The MITRE Corporation Semantic Interoperability Has Narrower Meaning Than DB Schemas, XML Schema Taxonomy Is Subclass of Structural Interoperability Is Sub-Classification of Syntactic Interoperability 9

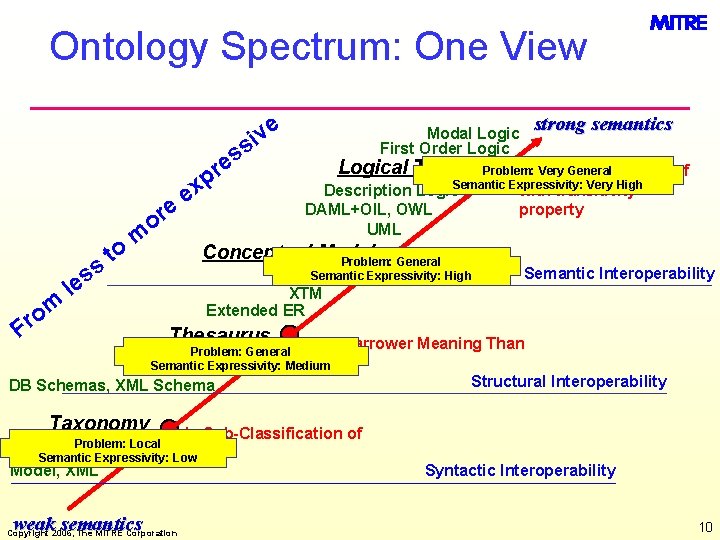
Ontology Spectrum: One View e iv s s e e or ss m o r to r p x e m Conceptual Model Problem: General Is Subclass of Semantic Interoperability Semantic Expressivity: High RDF/S XTM Extended ER le F strong semantics Modal Logic First Order Logical Theory Problem: Very General Is Disjoint Subclass of Semantic Expressivity: Very High with transitivity Description Logic DAML+OIL, OWL property UML Thesaurus Has Narrower Meaning Than Problem: General ER Semantic Expressivity: Medium DB Schemas, XML Schema Taxonomy Is Sub-Classification of Problem: Local Relational Semantic Expressivity: Low Model, XML weak semantics Copyright 2006, The MITRE Corporation Structural Interoperability Syntactic Interoperability 10

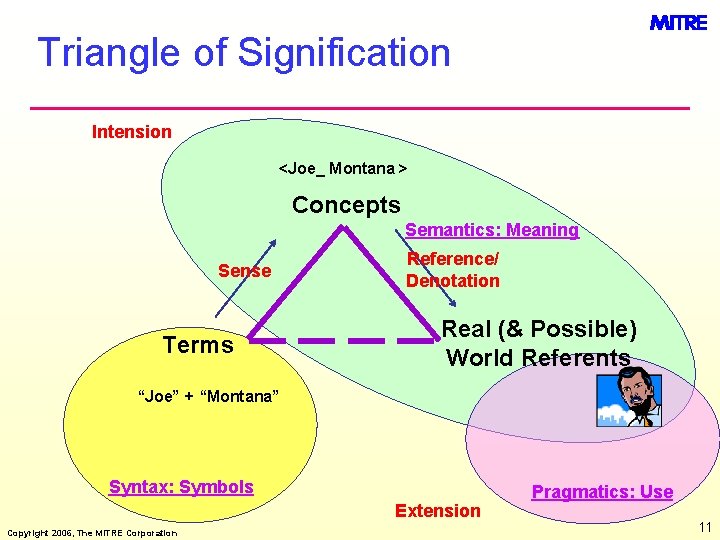
Triangle of Signification Intension <Joe_ Montana > Concepts Semantics: Meaning Sense Terms Reference/ Denotation Real (& Possible) World Referents “Joe” + “Montana” Syntax: Symbols Extension Copyright 2006, The MITRE Corporation Pragmatics: Use 11

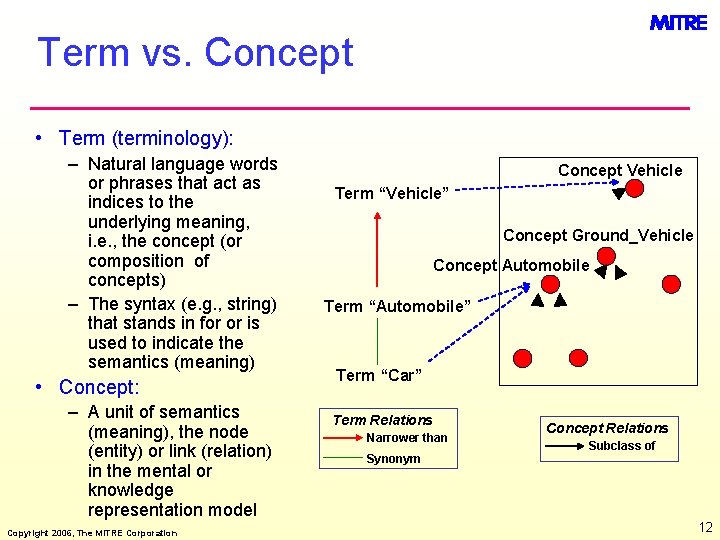
Term vs. Concept • Term (terminology): – Natural language words or phrases that act as indices to the underlying meaning, i. e. , the concept (or composition of concepts) – The syntax (e. g. , string) that stands in for or is used to indicate the semantics (meaning) • Concept: – A unit of semantics (meaning), the node (entity) or link (relation) in the mental or knowledge representation model Copyright 2006, The MITRE Corporation Concept Vehicle Term “Vehicle” Concept Ground_Vehicle Concept Automobile Term “Automobile” Term “Car” Term Relations Narrower than Synonym Concept Relations Subclass of 12

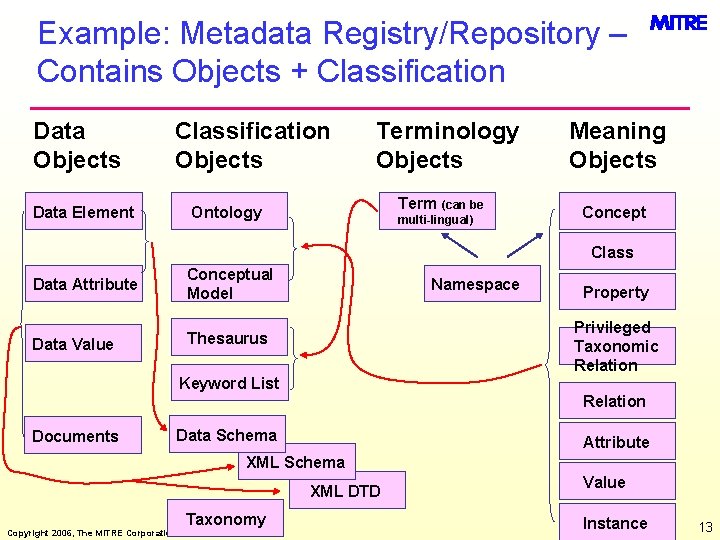
Example: Metadata Registry/Repository – Contains Objects + Classification Data Objects Classification Objects Data Element Terminology Objects Term (can be Ontology multi-lingual) Meaning Objects Concept Class Data Attribute Conceptual Model Data Value Thesaurus Namespace Property Privileged Taxonomic Relation Keyword List Relation Documents Data Schema Attribute XML Schema XML DTD Copyright 2006, The MITRE Corporation Taxonomy Value Instance 13

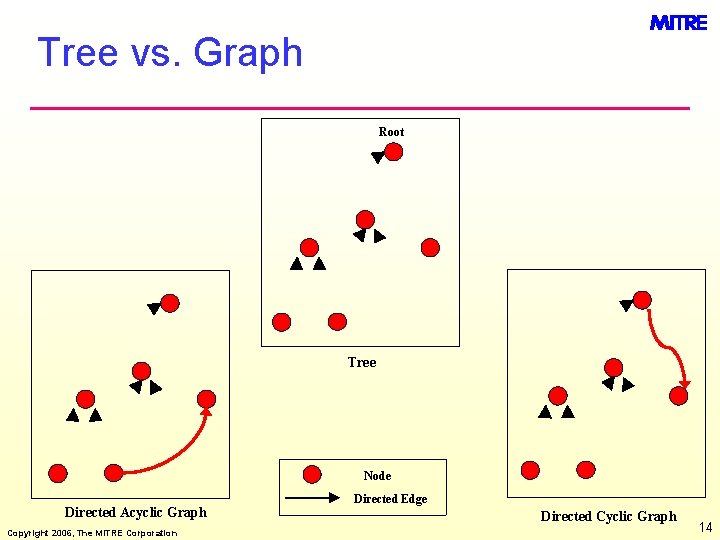
Tree vs. Graph Root Tree Node Directed Acyclic Graph Copyright 2006, The MITRE Corporation Directed Edge Directed Cyclic Graph 14

Taxonomy: Definition • Taxonomy: – A way of classifying or categorizing a set of things, i. e. , a classification in the form of a hierarchy (tree) • IT Taxonomy: – The classification of information entities in the form of a hierarchy (tree), according to the presumed relationships of the real world entities which they represent • Therefore: A taxonomy is a semantic (term or concept) hierarchy in which information entities are related by either: – The subclassification of relation (weak taxonomies) or – The subclass of relation (strong taxonomies) for concepts or the narrower than relation (thesauri) for terms – Only the subclass/narrower than relation is a subsumption (generalization/specialization) relation – Subsumption (generalization/specialization) relation: the mathematical subset relation – Mathematically, strong taxonomies, thesauri, conceptual models, and logical theories are minimally Partially Ordered Sets (posets), i. e. , they are ordered by the subset relation • They may be mathematically something stronger (conceptual models and logical theories) Copyright 2006, The MITRE Corporation 15

Taxonomies: Weak Example: Your Folder/Directory Structure • No consistent semantics for parent-child relationship: arbitrary Subclassification Relation • NOT a generalization / specialization taxonomy Copyright 2006, The MITRE Corporation Example: UNSPSC 16

Taxonomies: Strong • Consistent semantics for parentchild relationship: Narrower than (terms) or Subclass (concepts) Relation • A generalization/specialization taxonomy • For concepts: Each information entity is distinguished by a property of the entity that makes it unique as a subclass of its parent entity (a synonym for property is attribute or quality) • For terms: each child term implicitly refers to a concept which is the subset of the concept referred to by its parent term Copyright 2006, The MITRE Corporation H A M M E R Claw Ball Peen Sledge • What are the distinguishing properties between these three hammers? – Form (physical property) – Function (functional property) • “Purpose proposes property” (form follows function) – for human artifacts, at 17 least

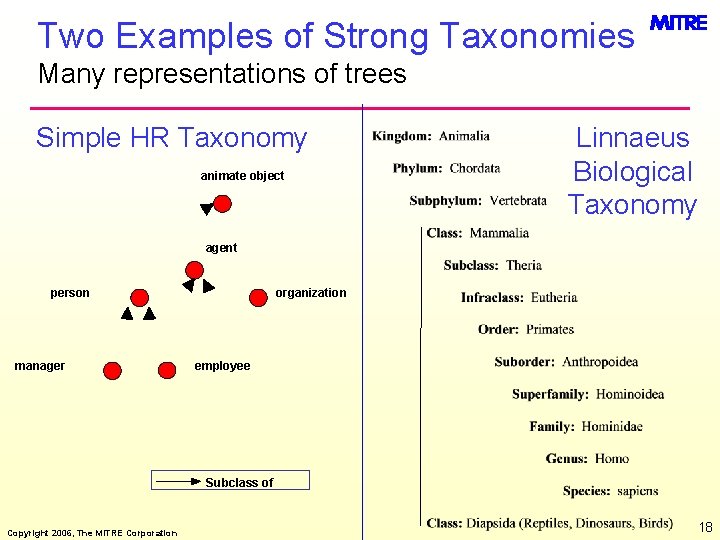
Two Examples of Strong Taxonomies Many representations of trees Simple HR Taxonomy animate object Linnaeus Biological Taxonomy agent person manager organization employee Subclass of Copyright 2006, The MITRE Corporation 18

Another, mostly strong Taxonomy: Dewey Decimal System Copyright 2006, The MITRE Corporation 19

When is a Taxonomy enough? • Weak taxonomy: – When you want semantically arbitrary parent-child term or concept relations, when the subclassification relation is enough – I. e. , sometimes you just want users to navigate down a hierarchy for your specific purposes, e. g, a quasi-menu system where you want them to see locally (low in the taxonomy) what you had already displayed high in the taxonomy – Application-oriented taxonomies are like this – Then, in general, you are using weak term relations because the nodes are not really meant to be concepts, but only words or phrases that will be significant to the user or you as a classification devise • Strong taxonomy: – When you really want to use the semantically consistent narrower-than (terms) or subclass (concepts) relation (a true subsumption or subset relation) – When you want to partition your general conceptual space – When you want individual conceptual buckets – Note: the subclass relation only applies to concepts; it is not equivalent (but is similar) to the narrower-than relation that applies to terms in thesauri • You need more than a taxonomy if you need to either: – Using narrower than relation: Define term synonyms and cross-references to other associated terms, or – Using subclass relation: Define properties, attributes and values, relations, constraints, rules, on concepts Copyright 2006, The MITRE Corporation 20

Thesaurus: Definition • From ANSI INISO 239. 19 -1993, (Revision of 239. 194980): – A thesaurus is a controlled vocabulary arranged in a known order and structured so that equivalence, homographic, hierarchical, and associative relationships among terms are displayed clearly and identified by standardized relationship indicators – The primary purposes of a thesaurus are to facilitate retrieval of documents and to achieve consistency in the indexing of written or otherwise recorded documents and other items • Four Term Semantic Relationships: – – Equivalence: synonymous terms Homographic: terms spelled the same Hierarchical: a term which is broader or narrower than another term Associative: related term • A consistent semantics for the hierarchical parent-child relationship: broader than, narrower than • This hierarchical ordering is a Subsumption (i. e. , generalization/specialization) relation • Can view just the narrower-than subsumption hierarchy as a term taxonomy • Unlike Strong subclass-based Taxonomy, Conceptual Model, & Logical Theory: the relation is between Terms, NOT Concepts Copyright 2006, The MITRE Corporation 21

Thesaural Term Relationships Copyright 2006, The MITRE Corporation 22

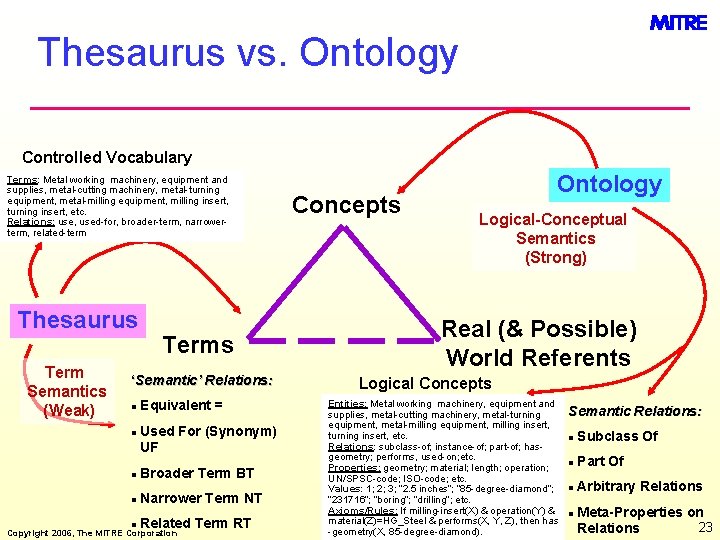
Thesaurus vs. Ontology Controlled Vocabulary Terms: Metal working machinery, equipment and supplies, metal-cutting machinery, metal-turning equipment, metal-milling equipment, milling insert, turning insert, etc. Relations: use, used-for, broader-term, narrowerterm, related-term Thesaurus Term Semantics (Weak) Terms ‘Semantic’ Relations: l l Equivalent = Used For (Synonym) UF l Broader Term BT l Narrower Term NT l Related Term RT Copyright 2006, The MITRE Corporation Concepts Ontology Logical-Conceptual Semantics (Strong) Real (& Possible) World Referents Logical Concepts Entities: Metal working machinery, equipment and supplies, metal-cutting machinery, metal-turning equipment, metal-milling equipment, milling insert, turning insert, etc. Relations: subclass-of; instance-of; part-of; hasgeometry; performs, used-on; etc. Properties: geometry; material; length; operation; UN/SPSC-code; ISO-code; etc. Values: 1; 2; 3; “ 2. 5 inches”; “ 85 -degree-diamond”; “ 231716”; “boring”; “drilling”; etc. Axioms/Rules: If milling-insert(X) & operation(Y) & material(Z)=HG_Steel & performs(X, Y, Z), then has -geometry(X, 85 -degree-diamond). Semantic Relations: l Subclass Of l Part Of l Arbitrary Relations l Meta-Properties on 23 Relations

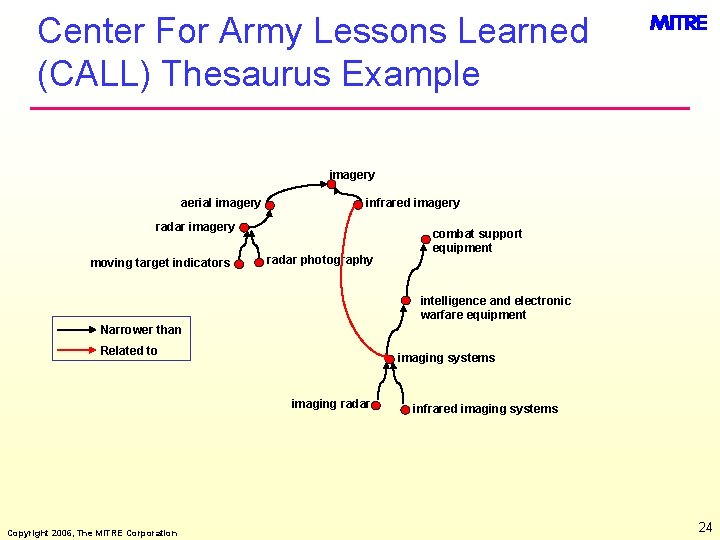
Center For Army Lessons Learned (CALL) Thesaurus Example imagery aerial imagery infrared imagery radar imagery moving target indicators radar photography combat support equipment intelligence and electronic warfare equipment Narrower than Related to imaging systems imaging radar Copyright 2006, The MITRE Corporation infrared imaging systems 24

When is a Thesaurus enough? • When you don’t need to define the concepts of your model, but only the terms that refer to those concepts, i. e. , to at least partially index those concepts • Ok, what does that mean? • If you need an ordered list of terms and their synonyms and loose connections to other terms (cross-references) • Examples: – If you need to use term buckets (sets or subsets) to use for term expansion in a keyword-based search engine – If you need a term classification index for a registry/repository, to guarantee uniqueness of terms and synonyms within a Community of Interest or namespace that might point to/index a concept node • You need more than a thesaurus if you need to define properties, attributes and values, relations, constraints, rules, on concepts – You need either a conceptual model (weak ontology) or a logical theory (strong ontology) Copyright 2006, The MITRE Corporation 25

Conceptual Models: Weak Ontologies • Many conceptual domains cannot be expressed adequately with a taxonomy (nor with a thesaurus, which models term relationships, as opposed to concept relationships) • Conceptual models seek to model a portion of a domain that a database must contain data for or a system (or, recently, enterprise) must perform work for, by providing users with the type of functionality they require in that domain • UML is paradigmatic modeling language • Drawbacks: – Models mostly used for documentation, required human semantic interpretation – Limited machine usability because cannot directly interpret semantically – Primary reason: there is no Logic that UML is based on • You need more than a Conceptual Model if you need machineinterpretability (more than machine-processing) – You need a logical theory (high-end ontology) Copyright 2006, The MITRE Corporation 26

Conceptual Model: UML Example Human Resource Conceptual Model Copyright 2006, The MITRE Corporation 27

Logical Theories: Strong Ontologies • Can be either Frame-based or Axiomatic – Frame-based: node-and-link structured in languages which hide the logical expressions, entity-centric, like object-oriented modeling, centering on the entity class, its attributes, properties, relations/associations, and constraints/rules – Axiomatic: axiom/rule-structured in languages which expose the logical expressions, non-entity-centric, so axioms that refer to entities (classes, instances, their attributes, properties, relations, constraint/rules) can be distributed Copyright 2006, The MITRE Corporation 28

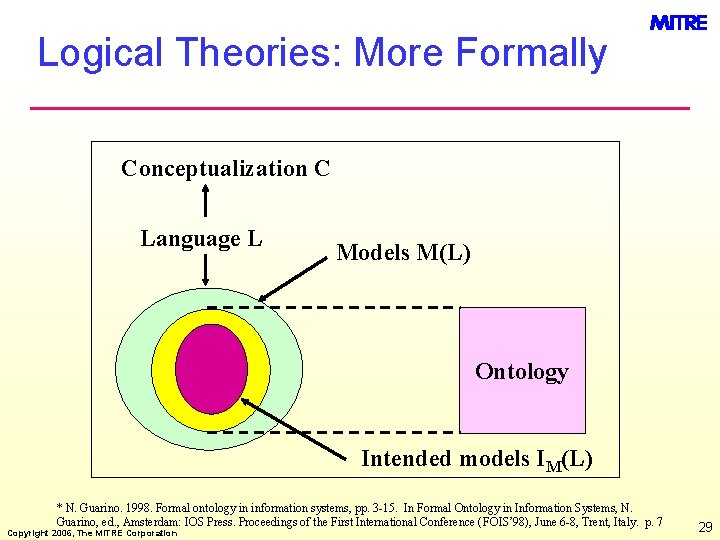
Logical Theories: More Formally Conceptualization C Language L Models M(L) Ontology Intended models IM(L) * N. Guarino. 1998. Formal ontology in information systems, pp. 3 -15. In Formal Ontology in Information Systems, N. Guarino, ed. , Amsterdam: IOS Press. Proceedings of the First International Conference (FOIS’ 98), June 6 -8, Trent, Italy. p. 7 Copyright 2006, The MITRE Corporation 29

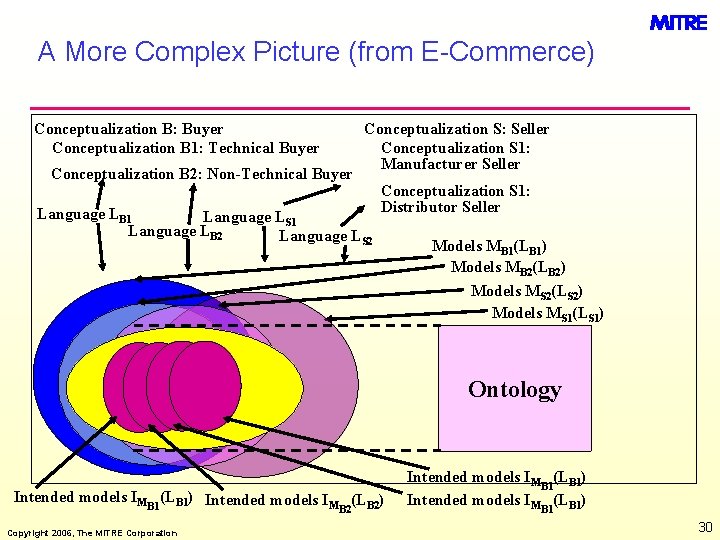
A More Complex Picture (from E-Commerce) Conceptualization B: Buyer Conceptualization B 1: Technical Buyer Conceptualization B 2: Non-Technical Buyer Language LB 1 Language LS 1 Language LB 2 Language L Conceptualization S: Seller Conceptualization S 1: Manufacturer Seller Conceptualization S 1: Distributor Seller S 2 Models MB 1(LB 1) Models MB 2(LB 2) Models MS 2(LS 2) Models MS 1(LS 1) Ontology Intended models IMB 1(LB 1) Intended models IM (LB 2) B 2 Copyright 2006, The MITRE Corporation Intended models IMB 1(LB 1) 30

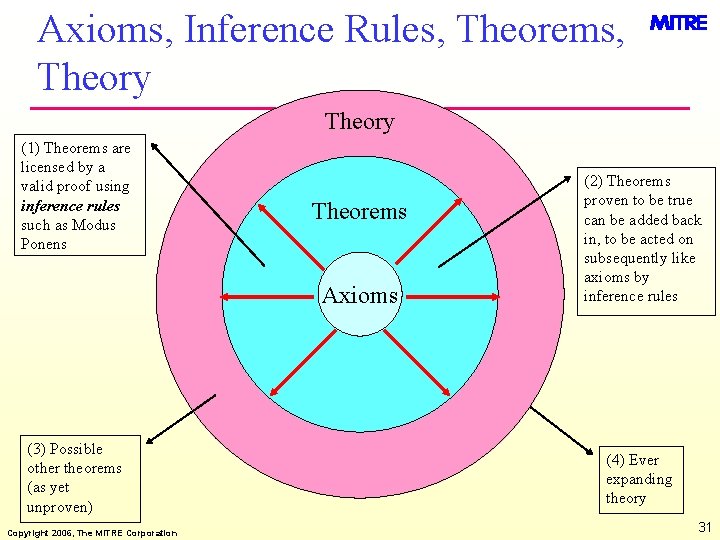
Axioms, Inference Rules, Theorems, Theory (1) Theorems are licensed by a valid proof using inference rules such as Modus Ponens Theorems Axioms (3) Possible other theorems (as yet unproven) Copyright 2006, The MITRE Corporation (2) Theorems proven to be true can be added back in, to be acted on subsequently like axioms by inference rules (4) Ever expanding theory 31

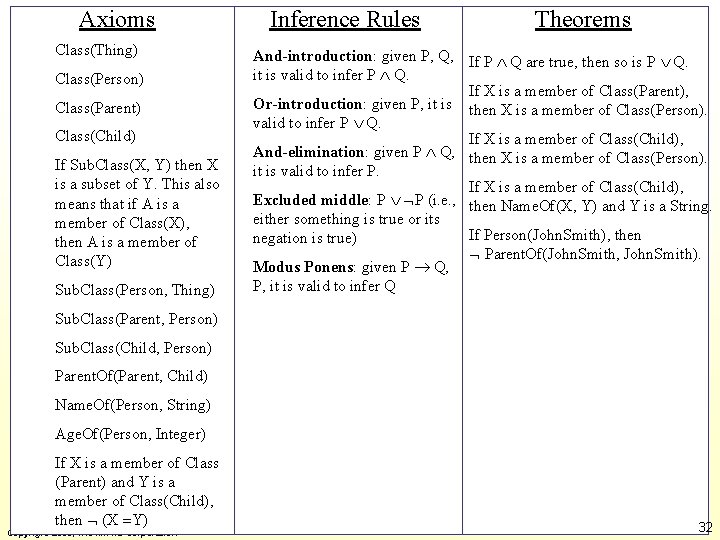
Axioms Class(Thing) Class(Person) Class(Parent) Class(Child) If Sub. Class(X, Y) then X is a subset of Y. This also means that if A is a member of Class(X), then A is a member of Class(Y) Sub. Class(Person, Thing) Inference Rules Theorems And-introduction: given P, Q, If P Q are true, then so is P Q. it is valid to infer P Q. If X is a member of Class(Parent), Or-introduction: given P, it is then X is a member of Class(Person). valid to infer P Q. If X is a member of Class(Child), And-elimination: given P Q, then X is a member of Class(Person). it is valid to infer P. If X is a member of Class(Child), Excluded middle: P P (i. e. , then Name. Of(X, Y) and Y is a String. either something is true or its If Person(John. Smith), then negation is true) Parent. Of(John. Smith, John. Smith). Modus Ponens: given P Q, P, it is valid to infer Q Sub. Class(Parent, Person) Sub. Class(Child, Person) Parent. Of(Parent, Child) Name. Of(Person, String) Age. Of(Person, Integer) If X is a member of Class (Parent) and Y is a member of Class(Child), then (X Y) Copyright 2006, The MITRE Corporation 32

Ontology Representation Levels Language Meta-Level to Object-Level Ontology (General) Meta-Level to Object-Level Copyright 2006, The MITRE Corporation Knowledge Base (Particular) 33

Copyright 2006, The MITRE Corporation 34

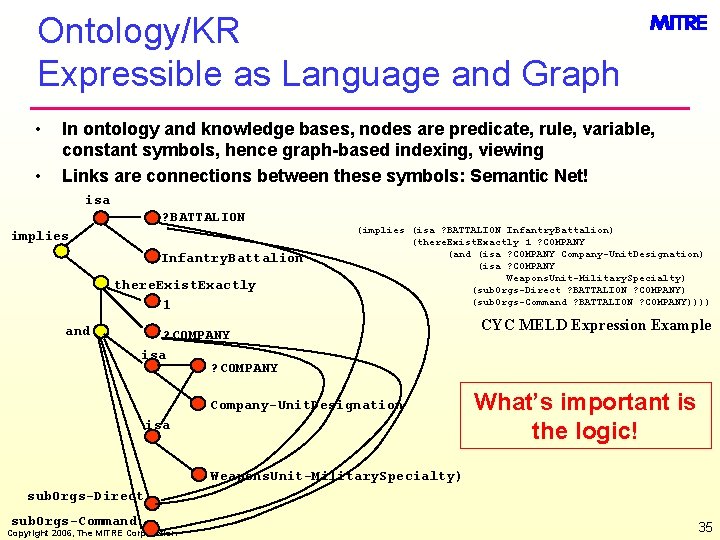
Ontology/KR Expressible as Language and Graph • • In ontology and knowledge bases, nodes are predicate, rule, variable, constant symbols, hence graph-based indexing, viewing Links are connections between these symbols: Semantic Net! isa ? BATTALION implies Infantry. Battalion there. Exist. Exactly 1 and (implies (isa ? BATTALION Infantry. Battalion) (there. Exist. Exactly 1 ? COMPANY (and (isa ? COMPANY Company-Unit. Designation) (isa ? COMPANY Weapons. Unit-Military. Specialty) (sub. Orgs-Direct ? BATTALION ? COMPANY) (sub. Orgs-Command ? BATTALION ? COMPANY)))) ? COMPANY isa ? COMPANY Company-Unit. Designation isa CYC MELD Expression Example What’s important is the logic! Weapons. Unit-Military. Specialty) sub. Orgs-Direct sub. Orgs-Command Copyright 2006, The MITRE Corporation 35

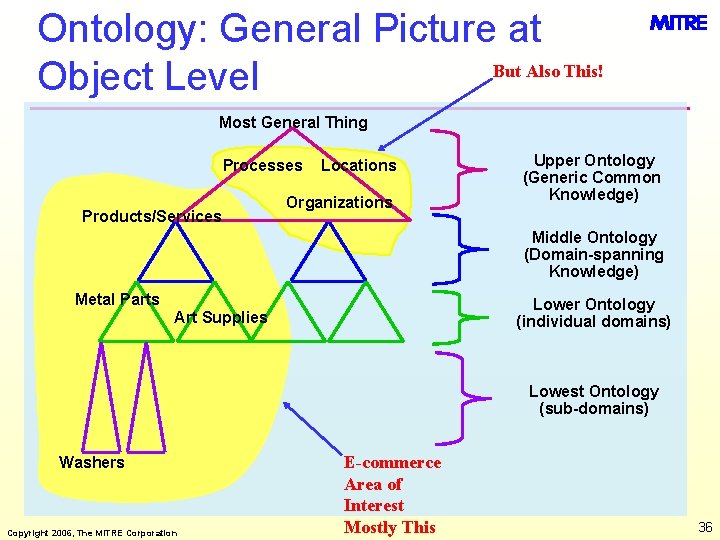
Ontology: General Picture at But Also This! Object Level Most General Thing Processes Products/Services Locations Organizations Upper Ontology (Generic Common Knowledge) Middle Ontology (Domain-spanning Knowledge) Metal Parts Lower Ontology (individual domains) Art Supplies Lowest Ontology (sub-domains) Washers Copyright 2006, The MITRE Corporation E-commerce Area of Interest Mostly This 36

Upper Ontological Distinctions 1 Focus here is on a few of the many possible upper ontological distinctions to be made • Descriptive vs. Revisionary: how one characterizes the ‘ontological stance’, i. e. , what an ontological engineering product is or should be – Revisionary: every model construct (concept) is a temporal object, i. e. , necessarily has temporal properties – Descriptive: model constructs are not necessarily temporal objects • Multiplicative vs. Reductionist: how one characterizes the kinds and number of concepts to be modeled – Multiplicative: Concepts can include anything that reality seems to require or any distinction that is useful to make – Reductionist: Concepts are reduced to the fewest primitives from which it is possible to generate complex reality Copyright 2006, The MITRE Corporation 37

Upper Ontological Distinctions 2 • Universal vs. Particular: the kinds of entities that ontologies address (the ‘universe of discourse’(s) of the ontology) – Universals: generic entities, which can have instances; classes – Particulars: specific entities, which are instances and can have no instances themselves • Continuant vs. Occurrent – Continuant: An entity whose identity continues to be recognizable over some extended interval of time (Sowa, 2000) – Occurrent: An entity that does not have a stable identity during any interval of time (Sowa, 2000) • 3 -dimensional (endurant) vs. 4 -dimensional (perdurant) – 3 D view/ Endurant: an object that goes through time (endures), with identity/essence-defining properties that perhaps depend on occurrent objects but are not essentially constituted by those occurrent objects – 4 D view/ Perdurant: an object that persists (perdures) through spacetime by way of having different temporal parts at what would be different times Copyright 2006, The MITRE Corporation 38

Upper Ontological Distinctions 3 • Part & Whole: Mereology, Topology, Mereotopology, the ‘part of’ relation – Mereology: parthood, what constitutes a ‘part’? – Topology: connectedness among objects, what constitutes ‘connected to’? – Mereotopology: the typical contemporary analysis of ‘part of’ says that the relation requires both the notion of part and the notion of connectedness; neither is sufficient alone to describe what we mean by saying that something is a part of another thing Copyright 2006, The MITRE Corporation 39

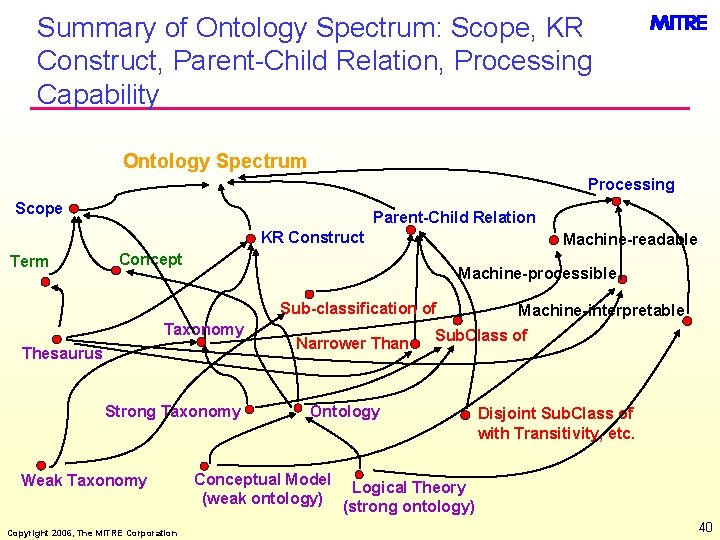
Summary of Ontology Spectrum: Scope, KR Construct, Parent-Child Relation, Processing Capability Ontology Spectrum Processing Scope Parent-Child Relation KR Construct Term Machine-readable Concept Machine-processible Sub-classification of Taxonomy Thesaurus Strong Taxonomy Weak Taxonomy Copyright 2006, The MITRE Corporation Narrower Than Machine-interpretable Sub. Class of Ontology Disjoint Sub. Class of with Transitivity, etc. Conceptual Model Logical Theory (weak ontology) (strong ontology) 40

What do we want the future to be? • 2100 A. D: models, models • There are no human-programmed programming languages • There are only Models Transformations, Compilations Ontological Models Knowledge Models Belief Models Application Models Presentation Models Target Platform Models Executable Code Copyright 2006, The MITRE Corporation I N F R A S T R U C T U R E 41

Contact Questions? lobrst@mitre. org Copyright 2006, The MITRE Corporation 42

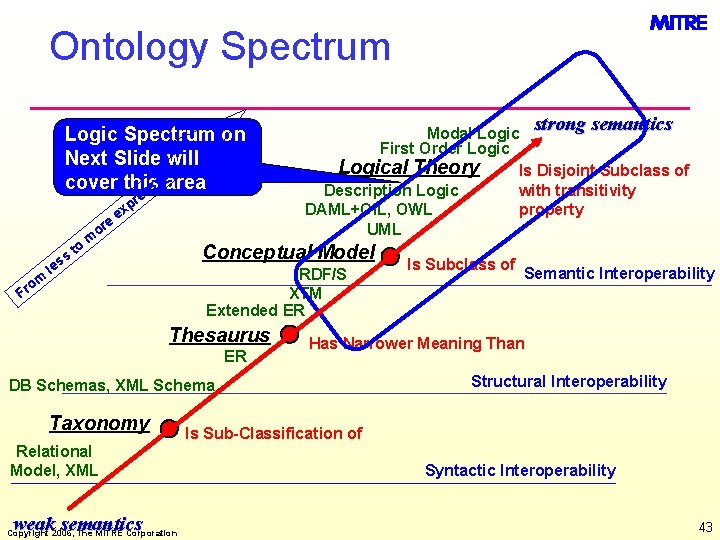
Ontology Spectrum Logic Spectrum on Next Slide will e ivarea cover this s s re e or m ro ss le to p ex m strong semantics Modal Logic First Order Logical Theory Is Disjoint Subclass of with transitivity Description Logic DAML+OIL, OWL property UML Conceptual Model RDF/S XTM Extended ER F Thesaurus ER Relational Model, XML weak semantics Copyright 2006, The MITRE Corporation Semantic Interoperability Has Narrower Meaning Than DB Schemas, XML Schema Taxonomy Is Subclass of Structural Interoperability Is Sub-Classification of Syntactic Interoperability 43

Logic Spectrum: Classical Logics: PL to HOL e or m o Fr ss le to pr x e v si e i og Higher Order Logic (HOL) cs L es m Second Order Logic (SOL) Modal Predicate Logic (Quantified Modal Logic) First-Order Logic (FOL): Predicate Logic, Predicate Calculus Logic Programming (Horn Clauses) Description Logics Modal Propositional Logic (PL) most expressive SOL + Complex Types + Higher-order Predicates (i. e. , those that take one or more other predicates as arguments) FOL + Quantifiers ( , ) over Predicates FOL + Modal operators PL + Predicates + Functions + Individuals + Quantifiers ( , ) over Individuals Syntactic Restriction of FOL Decidable fragments of FOL: unary predicates (concepts) & binary relations (roles) [max 3 vars] PL + Modal operators ( , ): necessity/possibility, obligatory/permitted, future/past, etc. Axiomatic systems: K, D, T, B, S 4, S 5 Substructural Logics: focus on structural rules Propositions (True/False) + Logical Connectives ( , , ) less expressive Copyright 2006, The MITRE Corporation 44

Logic Spectrum: Semantic Web Languages: Ontologies & Rules e or om ss le to pr x e v si e i og cs most expressive L es m Higher Order Logic (HOL) Second Order Logic (SOL) Modal Predicate Logic (Quantified Modal Logic) SOL extensions First-Order Logic (FOL): Predicate Logic, Predicate OWL-FOL Calculus SWRL OWL + Horn-like Rules Logic Programming (Horn Clauses) OWL Full Almost FOL, but Classes as Instances goes to SOL OWL DL Mostly SHOIN(D): Close to the SHIQ and SHOQ Description Logics OWL Lite Almost SHIF(D) (technically, it’s a variant of SHIN(D) Modal Propositional RDF/S Positive existential subset of FOL: no negation, universal Logic quantification Fr Propositional Logic (PL) Rule. ML less expressive Expressed Copyright 2006, The MITRE Corporation Linear Logic: consume antecedents Substructural Logics: focus on structural rules syntactically in XML, requires binding to a logic, ranges over all logics 45

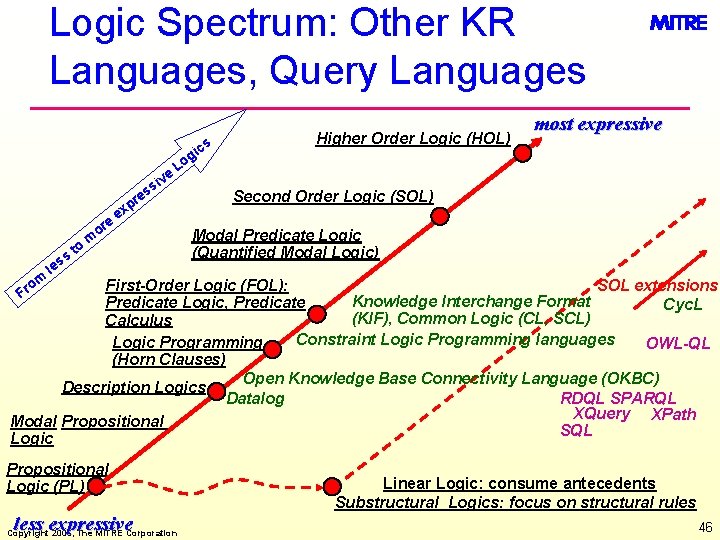
Logic Spectrum: Other KR Languages, Query Languages e or om ss le to pr x e v si e i og cs Higher Order Logic (HOL) most expressive L es m Second Order Logic (SOL) Modal Predicate Logic (Quantified Modal Logic) SOL extensions First-Order Logic (FOL): Knowledge Interchange Format Predicate Logic, Predicate Cyc. L (KIF), Common Logic (CL, SCL) Calculus Constraint Logic Programming languages Logic Programming OWL-QL (Horn Clauses) Open Knowledge Base Connectivity Language (OKBC) Description Logics Datalog RDQL SPARQL XQuery XPath Modal Propositional SQL Logic Fr Propositional Logic (PL) less expressive Copyright 2006, The MITRE Corporation Linear Logic: consume antecedents Substructural Logics: focus on structural rules 46