The Normal Distribution The Log Normal Distribution Geometric

The Normal Distribution & The Log Normal Distribution & Geometric Mean • Level: Intermediate • Version No: 1 • Version Date: June 2013 Rehena Sultana, M. Sc (Statistics) Associate Biostatistician Duke-NUS Medical School

Disclaimer/Liability • The information provided in the VAP is made available in good faith and is derived from sources believed to be reliable and accurate at the time of release. • The materials presented on the VAP may include links to external Internet sites. These external information sources are outside the control of Duke-NUS. The user of the Internet links is responsible for making his or her own decision about the accuracy, reliability and correctness of the information found. • In no event shall Duke-NUS be liable for any indirect, special, incidental, or consequential damages arising out of any use of reliance of any information contained in the VAP. Nor does Duke-NUS assume any responsibility for failure or delay in updating or removing the information contained in the VAP. • Moreover, information provided on the VAP does not constitute medical advice or treatment nor should it be considered as a replacement of the patient/physician relationship or a physician’s professional judgment. Duke. NUS expressly disclaims all liability for treatment, diagnosis, decisions and actions taken or not taken in reliance upon information contained in the VAP. This work is licensed under a Creative Commons Attribution-Non. Commercial-No. Derivs 3. 0 Unported License To view a copy of this license, visit [http: //creativecommons. org/licenses/by-nc-nd/3. 0/]

Financial Disclosures • No Disclosures

Learning Objectives • Normal Distribution – Properties – Standard Normal Distribution – The Central Limit Theorem • Log Normal distribution – Properties – Geometric mean
The Normal Distribution

Outline Normal distribution • Properties • The standard normal distribution • Application • Central Limit Theorem

Definition: Normal Distribution • Discovered by De-Moivre in 1733. • A continuous probability distribution. – Continuous variable uncountable number of values. – Probability distribution realization of data
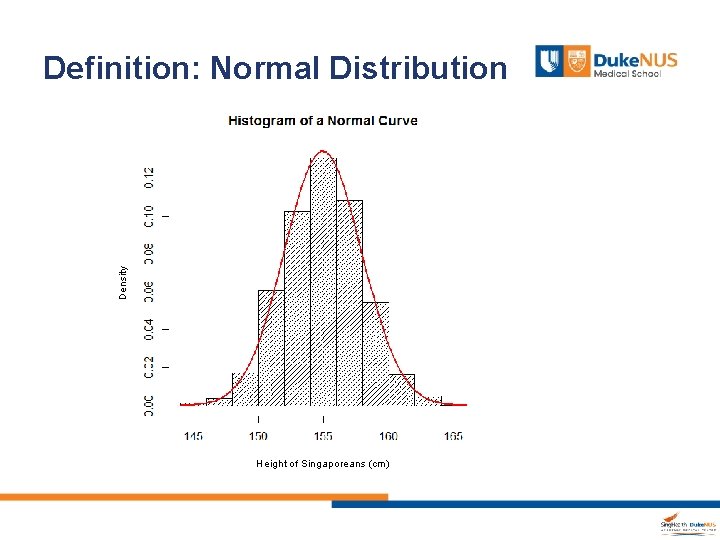
Density Definition: Normal Distribution Height of Singaporeans (cm)
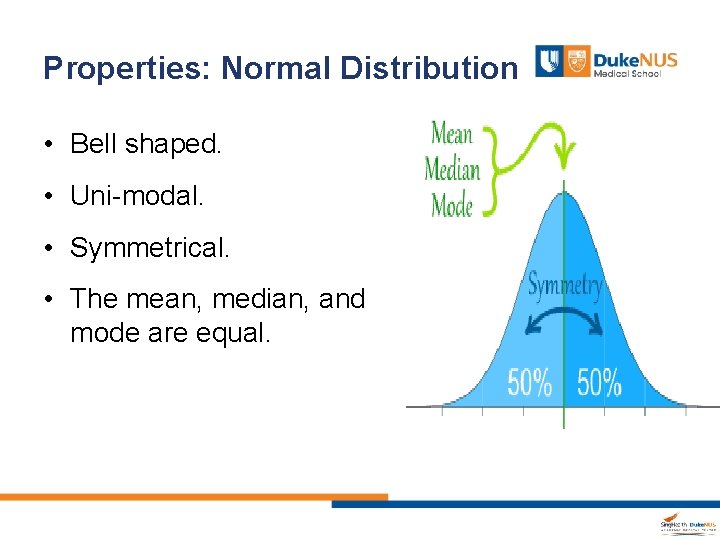
Properties: Normal Distribution • Bell shaped. • Uni-modal. • Symmetrical. • The mean, median, and mode are equal.

Properties: Normal Distribution (con’t) • Asymptotic to X – axis. • The amount of variation in the random variable determines the height and spread of the normal distribution. • If the random variable X follows normal distribution with mean and variance 2, then we write X ~ N( , 2). – and 2 are the parameters of the distribution.

Properties: Normal Distribution (con’t) • The probability density of X~N(µ, σ2) can be written as and = 3. 14 • If x ~ N(µ 1, 12) and y ~ N(µ 2, 22) and they are independent to each other, then x + y ~ N(µ 1 + µ 2, 12 + 22).
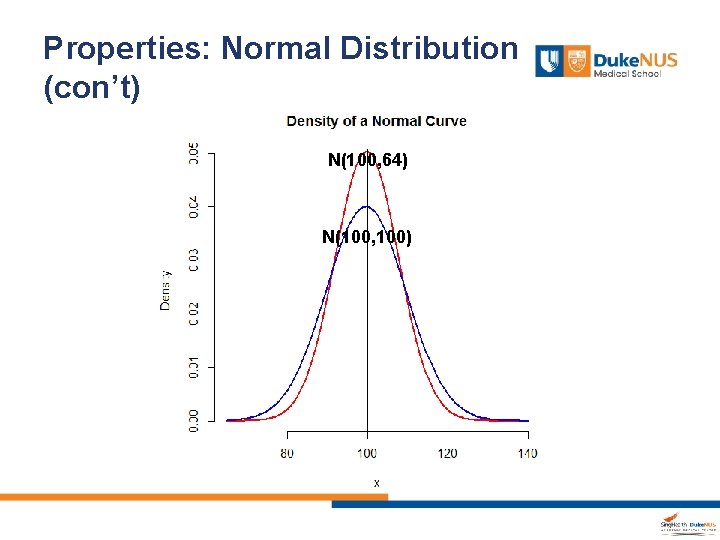
Properties: Normal Distribution (con’t) N(100, 64) N(100, 100) N(130, 100) N(100, 100)
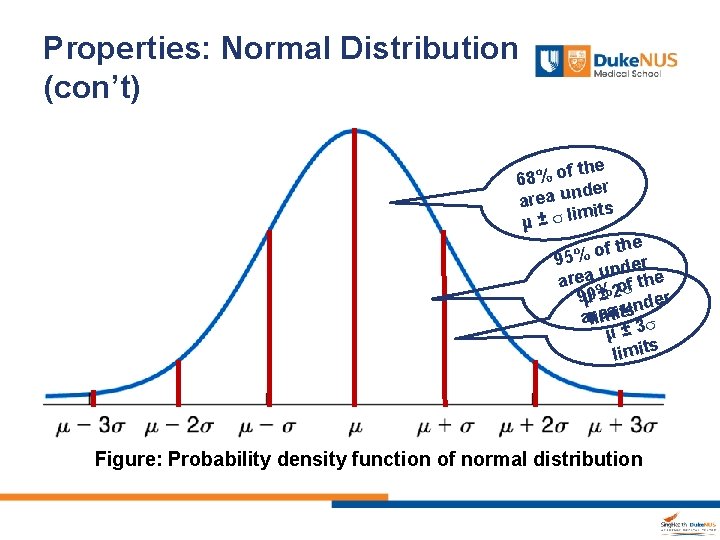
Properties: Normal Distribution (con’t) the f o % 68 er d n u a are mits i l ± µ the f o 95% er d n u area o f the ± 2 der 9µ 9 % usn a t i e r m i al 3 ± µ limits Figure: Probability density function of normal distribution

Standard Normal Distribution: Definition • If X ~ N(µ, σ2), then x any value in horizontal axis µ mean of the normal distribution σ sd of the normal distribution z scaled value. Z follows standard normal distribution. General notation for standard distribution is Z~N(0, 1).

Applications of normal distribution in Clinical Research (examples) • Height / Weight • IQ scores • Body temperature • Diastolic / systolic blood pressure • Repeated measurements of same quantity

Central Limit Theorem (CLT) If Xi (i = 1, . . , n) are independent random variables with mean µi and σi 2, then under central limit theorem, the random variable Sn= X 1+. . +Xn is asymptotically normal For the purpose of applying the central limit theorem, we will consider a sample size to be large when n > 30.

Application of CLT: Example A random sample of n = 64 observations are drawn from a population of mean µ = 15 and standard deviation = 4. As sample size is large enough we can easily apply CLT. Hence we can write
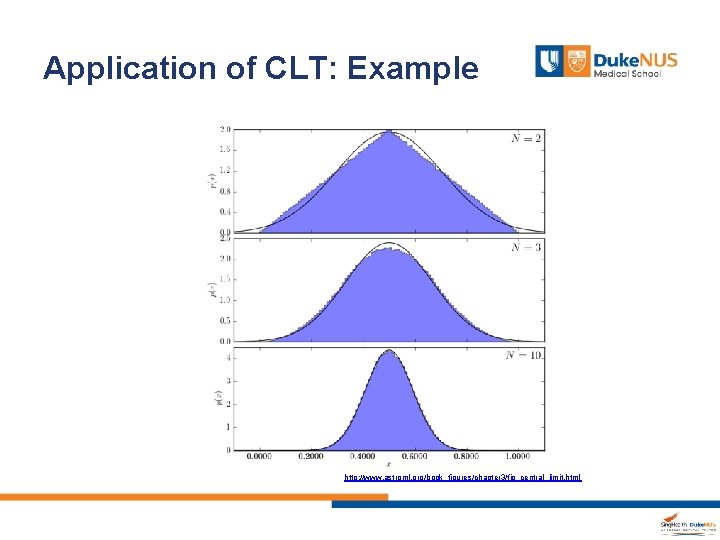
Application of CLT: Example http: //www. astroml. org/book_figures/chapter 3/fig_central_limit. html

Lognormal Distribution & Geometric Mean

Outline • Log normal distribution – Property – Application • Geometric mean

Application of Log normal distribution in Clinical Research (examples) • Latency period of diseases like chicken pox, bacterial food poisoning, amoebic dysentery • Survival times of cancer diagnosis • Age of onset of disease e. g. Alzheimer

Definition: Log Normal Distribution • A continuous probability distribution. • If X is normal distribution, then y = ex follows log normal distribution. • General Notation: X ~ LN(µ, σ2) • Density function of X when X ~ LN(µ, 2) is: , x > 0

Properties: Log Normal Distribution • Mean: • Variance: • If Y ~ N(µ, σ2), then ey ~ LN(µ, σ2). • If Y ~ LN(µ, σ2), then log(X) ~ N(µ, σ2) • The product of two log normal distribution is also lognormal.
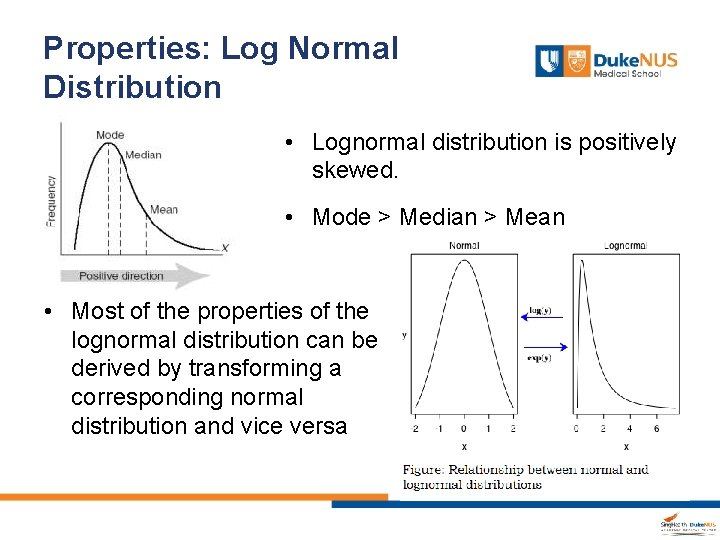
Properties: Log Normal Distribution • Lognormal distribution is positively skewed. • Mode > Median > Mean • Most of the properties of the lognormal distribution can be derived by transforming a corresponding normal distribution and vice versa

Geometric Mean • Geometric mean of data set x 1, x 2, …, xn is • Log of the geometric mean is

Properties: Geometric Mean • As the log of the geometric mean is an average, we can apply CLT (under same assumption) • Geometric mean ≤ mean (arithmetic mean). • It gives comparatively more weight to small items. • It is not affected much by fluctuations of sampling.

Application of Geometric Mean • Rate of population growth. • Growth rate of infection rate. • Interest rate in bank. • To construct index numbers.

Geometric Mean: Example Suppose that in a population of interest, the prevalence of a disease rose 2% one year, then fell 1% in next year, then rose 2%, then rose 1%; since these factors act multiplicatively it makes sense to consider the geometric mean. (1. 02 x 0. 99 x 1. 02 x 1. 01)1/4 = 1. 01 Hence overall increased disease prevalence over these 4 years was 1%.

Summary • Lognormal distribution is always a better model for original data • Normal distribution is very common because of symmetry nature. • People like to use additive property compared to multiplicative property, so it makes sense to use geometric mean. • Defining the normal limits of a clinical measurement is not straightforward and requires clinical thinking.

Key References • Harvey Motulsky. Intuitive Biostatistics: A nonmathematical guide to statistical thinking (2 nd ed. ): Oxford • Aitchison J, Brown JAC. 1957. The Log-normal Distribution. Cambridge (UK): Cambridge University Press. • Wlodzimierz Bryc. Normal Distribution characterizations with applications: Lecture Notes in Statistics 1995, Vol 100 (Revised June 7, 2005)

Acknowledgements • Special Thanks to Ms. Shruti Shah for helping to amend our slides.

Thank you
- Slides: 32