The Normal Distribution If the three histograms shown

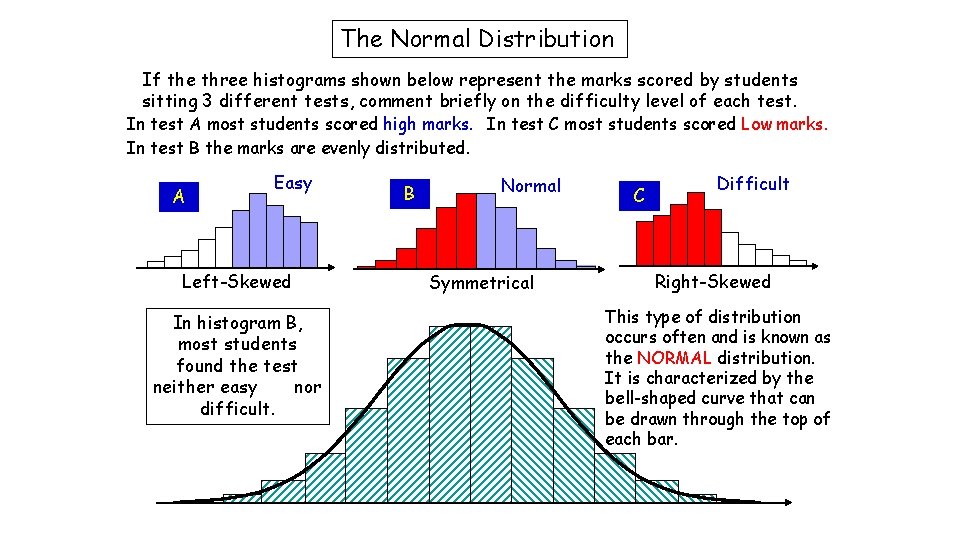
The Normal Distribution If the three histograms shown below represent the marks scored by students sitting 3 different tests, comment briefly on the difficulty level of each test. In test A most students scored high marks. In test C most students scored Low marks. In test B the marks are evenly distributed. A Easy Left-Skewed In histogram B, most students found the test neither easy nor difficult. B Normal Symmetrical C Difficult Right-Skewed This type of distribution occurs often and is known as the NORMAL distribution. It is characterized by the bell-shaped curve that can be drawn through the top of each bar.

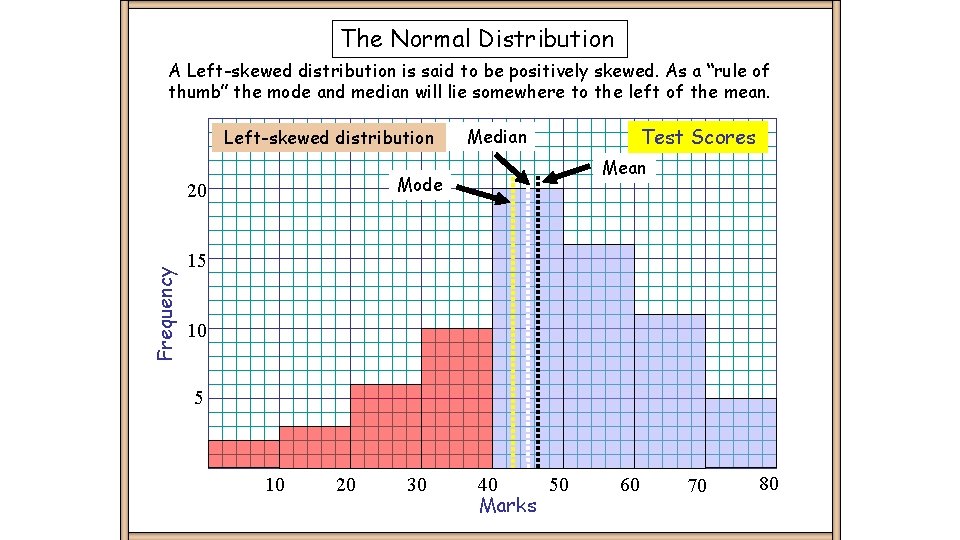
The Normal Distribution A Left-skewed distribution is said to be positively skewed. As a “rule of thumb” the mode and median will lie somewhere to the left of the mean. Left-skewed distribution Frequency Mean Mode 20 Test Scores Median 15 10 20 30 40 50 Marks 60 70 80

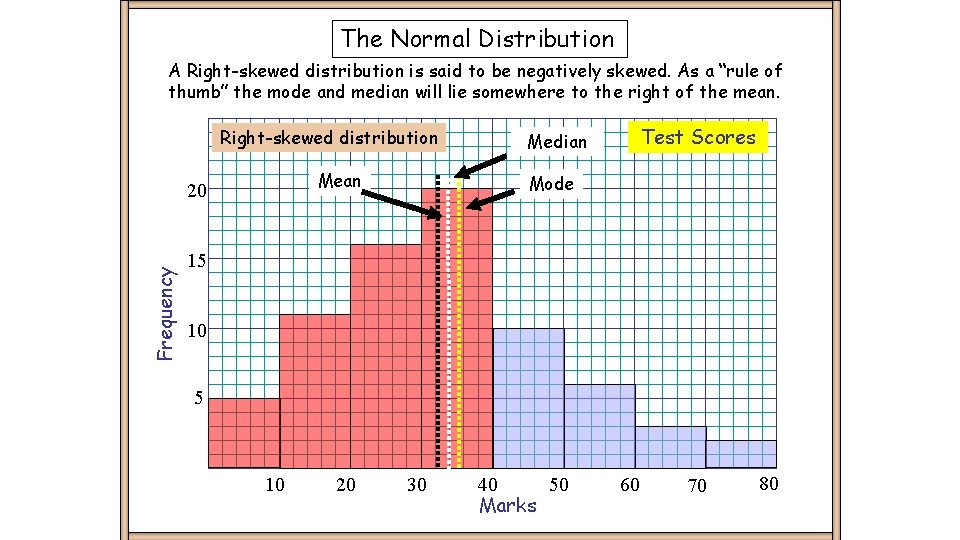
The Normal Distribution A Right-skewed distribution is said to be negatively skewed. As a “rule of thumb” the mode and median will lie somewhere to the right of the mean. Right-skewed distribution Mean Frequency 20 Test Scores Median Mode 15 10 20 30 40 50 Marks 60 70 80

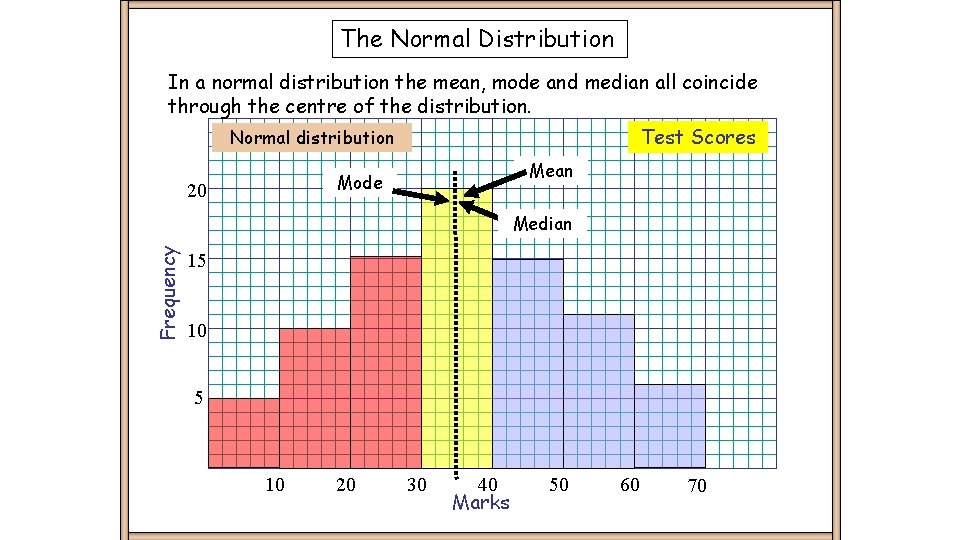
The Normal Distribution In a normal distribution the mean, mode and median all coincide through the centre of the distribution. Test Scores Normal distribution Mean Mode 20 Frequency Median 15 10 20 30 40 Marks 50 60 70

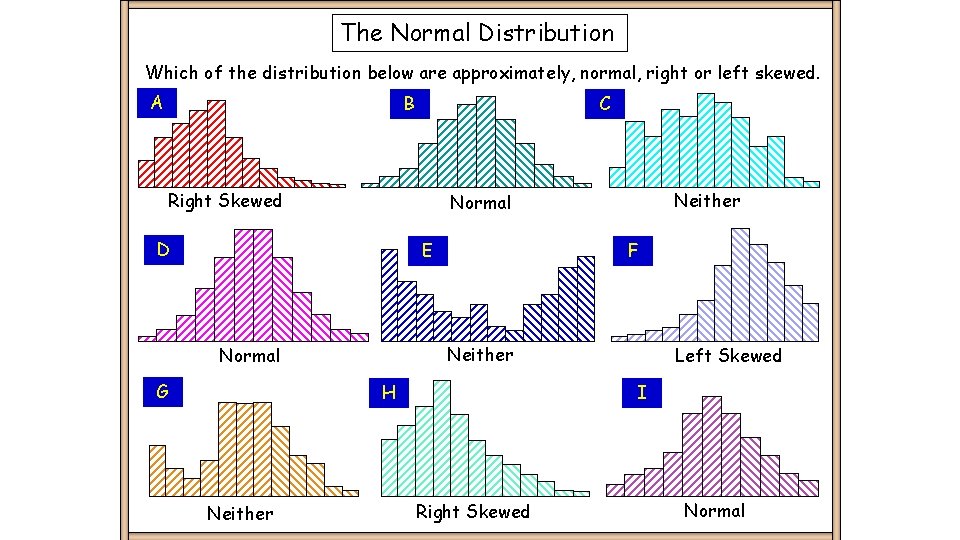
The Normal Distribution Which of the distribution below are approximately, normal, right or left skewed. A B C Right Skewed D E F Neither Normal G H Neither Normal Left Skewed I Right Skewed Normal