The Normal Distribution History Abraham de Moivre 1733

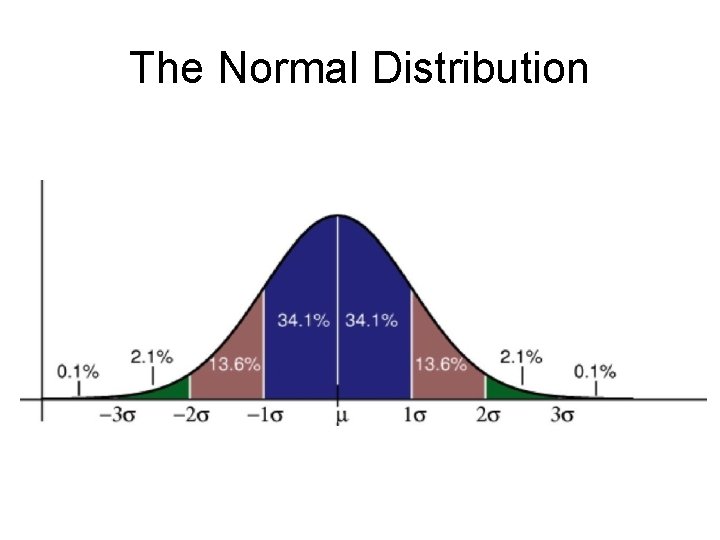
The Normal Distribution

History • Abraham de Moivre (1733) – consultant to gamblers. Pronunciation. • Pierre Simon Laplace – mathematician, astronomer, philosopher, determinist. • Carl Friedrich Gauss – mathematician and astronomer. • Adolphe Quetelet -- mathematician, astronomer, “social physics. ” Pronunciation.

Importance • Many variables are distributed approximately as the bell-shaped normal curve • The mathematics of the normal curve are well known and relatively simple. • Many statistical procedures assume that the scores came from a normally distributed population.

• Distributions of sums and means approach normality as sample size increases. • Many other probability distributions are closely related to the normal curve.

Using the Normal Curve • From its PDF (probability density function) we use integral calculus to find the probability that a randomly selected score would fall between value a and value b. • This is equivalent to finding what proportion of the total area under the curve falls between a and b.

The PDF • F(Y) is the probability density, aka the height of the curve at value Y. • There are only two parameters, the mean and the variance. • Normal distributions differ from one another only with respect to their mean and variance.

Avoiding the Calculus • Use the normal curve table in our text. • Use SPSS or another stats package. • Use an Internet resource.

IQ = 85, PR = ? • z = (85 - 100)/15 = -1. • What percentage of scores in a normal distribution are less than minus 1? • Half of the scores are less than 0, so you know right off that the answer is less than 50%. • Go to the normal curve table.
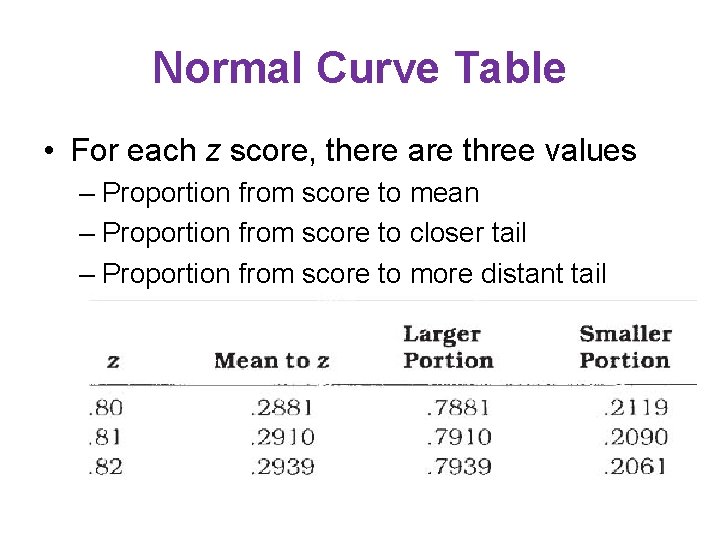
Normal Curve Table • For each z score, there are three values – Proportion from score to mean – Proportion from score to closer tail – Proportion from score to more distant tail
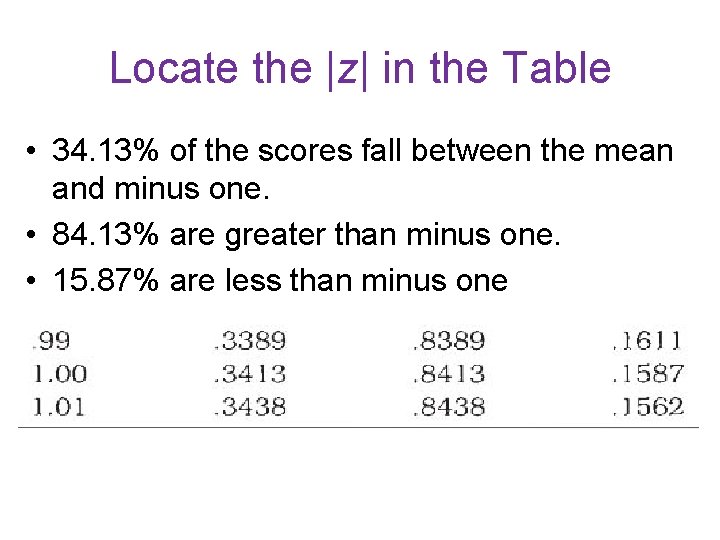
Locate the |z| in the Table • 34. 13% of the scores fall between the mean and minus one. • 84. 13% are greater than minus one. • 15. 87% are less than minus one

IQ =115, PR = ? • z = (115 – 100)/15 = 1. • We are above the mean so the answer must be greater than 50%. • The answer is 84. 13%.

85 < IQ < 115 • What percentage of IQ scores fall between 85 (z = -1) and 115 (z = 1)? • 34. 13% are between mean and -1. • 34. 13% are between mean and 1. • 68. 26% are between -1 and 1.

115 < IQ < 130 • What percentage of IQ scores fall between 115 (z = 1) and 130 (z = 2)? • 84. 13% fall below 1. • 97. 72% fall below 2. • 97. 72 – 84. 13 = 13. 59%

The Lowest 10% • What score marks off the lowest 10% of IQ scores ? • z = 1. 28 • IQ = 100 – 1. 28(15) = 80. 8

The Middle 50% • What scores mark off the middle 50% of IQ scores? • -. 67 < z <. 67; • 100 -. 67(15) = 90 • 100 +. 67(15) = 110
Online Calculator • This one is easy to use. Check it out. • http: //davidmlane. com/hyperstat/z_table. html
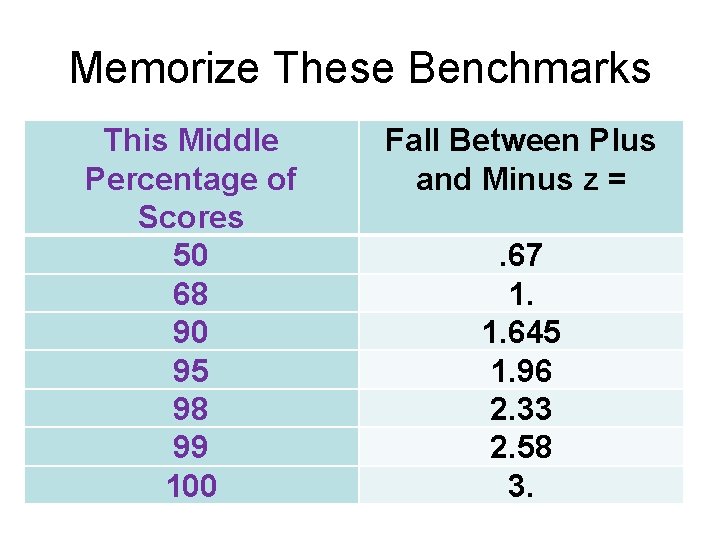
Memorize These Benchmarks This Middle Percentage of Scores 50 68 90 95 98 99 100 Fall Between Plus and Minus z =. 67 1. 1. 645 1. 96 2. 33 2. 58 3.
The Normal Distribution
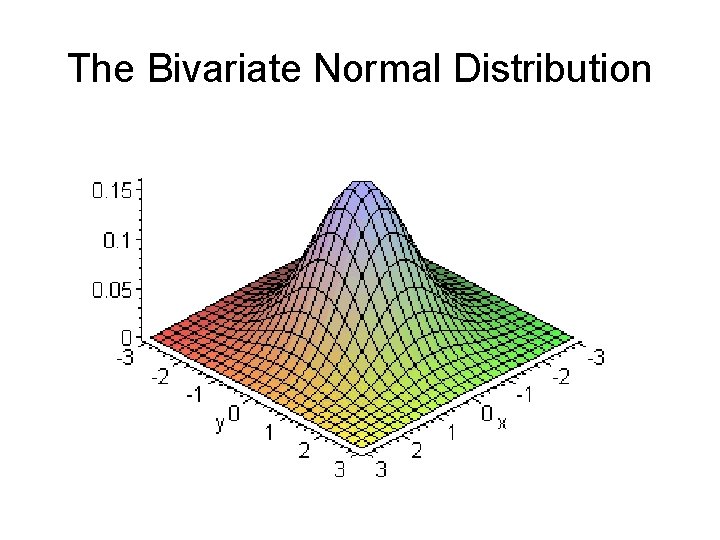
The Bivariate Normal Distribution

- Slides: 22