The NodeSearching Problem on Special Graphs chouhhmail cjcu

The Node-Searching Problem on Special Graphs 周信宏 長榮大學 資訊管理學系 chouhh@mail. cjcu. edu. tw IM. CJCU 1 Hsin-Hung Chou

Outline • • • IM. CJCU Introduction Properties of the problem Previous results Result on unicyclic graphs Conclusions 2 Hsin-Hung Chou

Outline • Introduction • graph searching problem • problem definition • • IM. CJCU Properties of the problem Previous results Result on unicyclic graphs Conclusions 3 Hsin-Hung Chou

Graph-Searching Problem l Graph-searching problem was first proposed by Parsons, 1976. l Goal: To find a search strategy using the least number of searchers to capture the fugitive. IM. CJCU 4 Hsin-Hung Chou

Problem Definition Operations: • Place a searcher • Remove a searcher • Move along an edge Clearing rules: • Move along an edge • Guard two endpoints of an edge IM. CJCU Variations: Operations Rules • Place Edge- • Remove • Move • Place Node- • Remove • Guard • Place Mixed- • Remove • Move • Guard 5 Hsin-Hung Chou

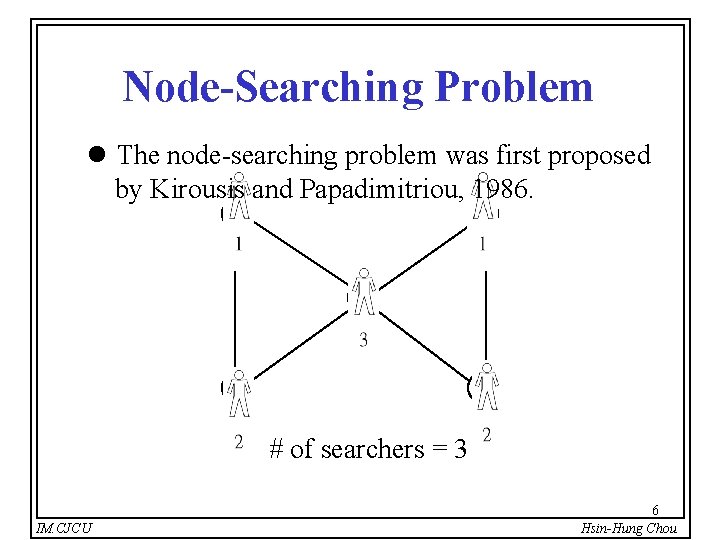
Node-Searching Problem l The node-searching problem was first proposed by Kirousis and Papadimitriou, 1986. a d c b e # of searchers = 3 IM. CJCU 6 Hsin-Hung Chou

Outline • Introduction • Properties of the problem • progressive strategy • related problems • Previous results • Result on unicyclic graphs • Conclusions IM. CJCU 7 Hsin-Hung Chou

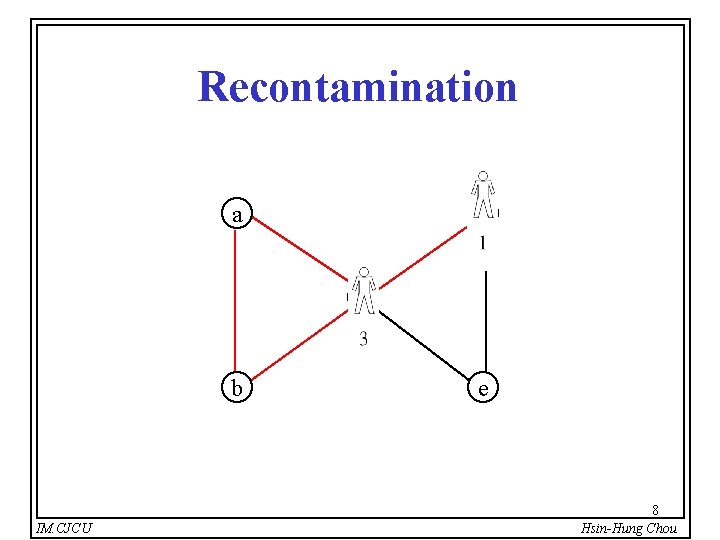
Recontamination a d c b IM. CJCU e 8 Hsin-Hung Chou

Progressive Strategy l Kirousis and Papadimitriou showed that there exists an optimal search strategy without recontamination for any graph. l There exists an optimal search strategy in which no vertex is visited twice by a searcher, and in which every searcher is deleted immediately after all the edges incident on it have been cleared. l We can only consider search strategies without recontamination. IM. CJCU 9 Hsin-Hung Chou

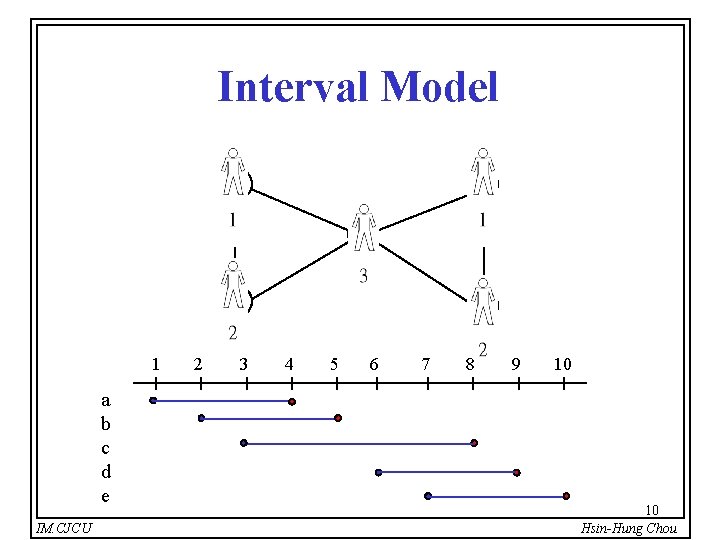
Interval Model a d c b 1 a b c d e IM. CJCU 2 3 e 4 5 6 7 8 9 10 10 Hsin-Hung Chou

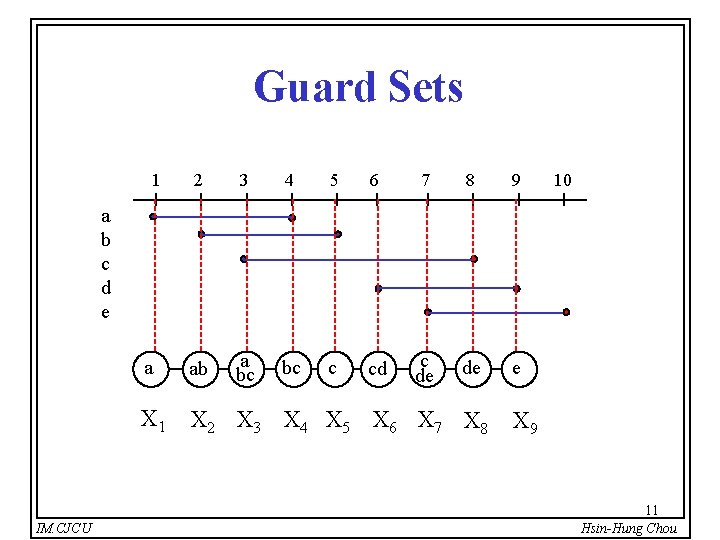
Guard Sets 1 2 3 4 5 6 7 8 9 a ab a bc bc c cd c de de e X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 10 a b c d e IM. CJCU X 9 11 Hsin-Hung Chou

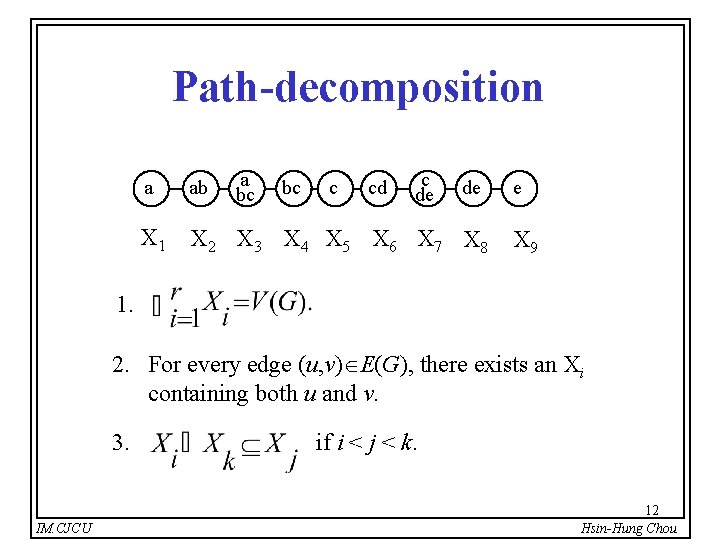
Path-decomposition a bc bc c c de a ab X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 cd de e X 9 1. 2. For every edge (u, v) E(G), there exists an Xi containing both u and v. 3. IM. CJCU if i < j < k. 12 Hsin-Hung Chou

Path-width Problem l The width of a path-decomposition is max { |Xi| | 1 i r} – 1. l The path-width of G is the minimum width over all path-decompositions of G. l The path-width of G is equal to the node-search number of G minus one. IM. CJCU 13 Hsin-Hung Chou

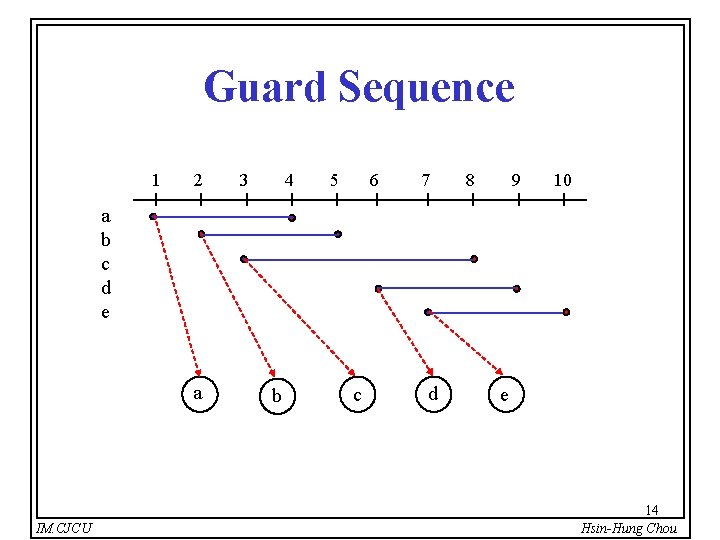
Guard Sequence 1 2 3 4 5 6 7 8 9 10 a b c d e a IM. CJCU b c d e 14 Hsin-Hung Chou

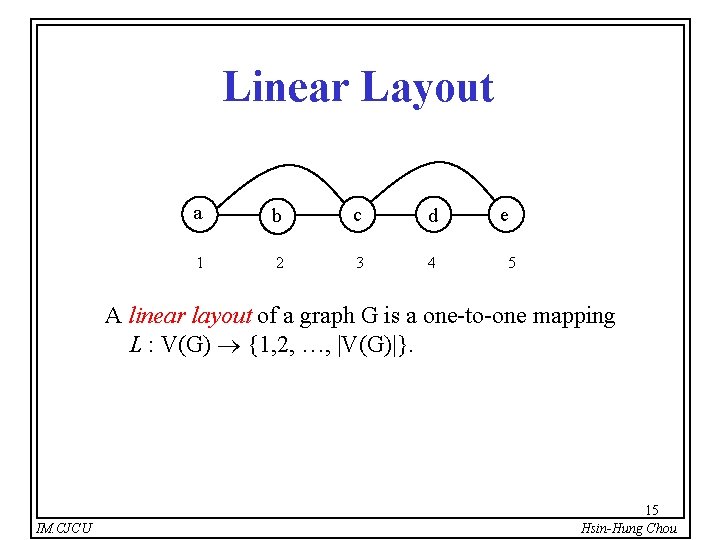
Linear Layout a b c d 1 2 3 4 e 5 A linear layout of a graph G is a one-to-one mapping L : V(G) {1, 2, …, |V(G)|}. IM. CJCU 15 Hsin-Hung Chou

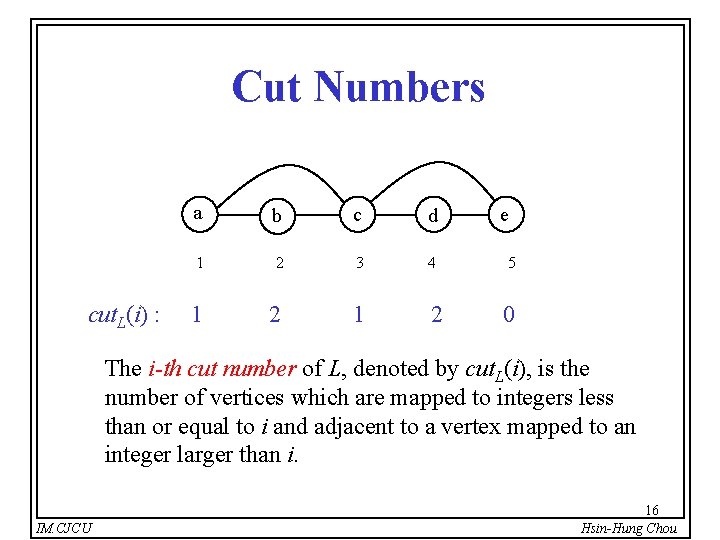
Cut Numbers cut. L(i) : a b c d 1 2 3 4 1 2 e 5 0 The i-th cut number of L, denoted by cut. L(i), is the number of vertices which are mapped to integers less than or equal to i and adjacent to a vertex mapped to an integer larger than i. IM. CJCU 16 Hsin-Hung Chou

Vertex Separation l The vertex separation with respect to G and L: vs. L(G) = max {cut. L(i) | 1 i |V(G)|}. l The vertex separation of G: vs(G) = min {vs. L(G) | L is a linear layout of G}. l The vertex separation of G is equal to the node-search number of G minus one. IM. CJCU 17 Hsin-Hung Chou

Related Problems l The node-searching problem is equivalent to • • • IM. CJCU path-width problem vertex separation problem interval thickness problem gate matrix layout problem narrowness problem 18 Hsin-Hung Chou

Outline • • • IM. CJCU Introduction Properties of the problem Previous results Result on unicyclic graphs Conclusions 19 Hsin-Hung Chou

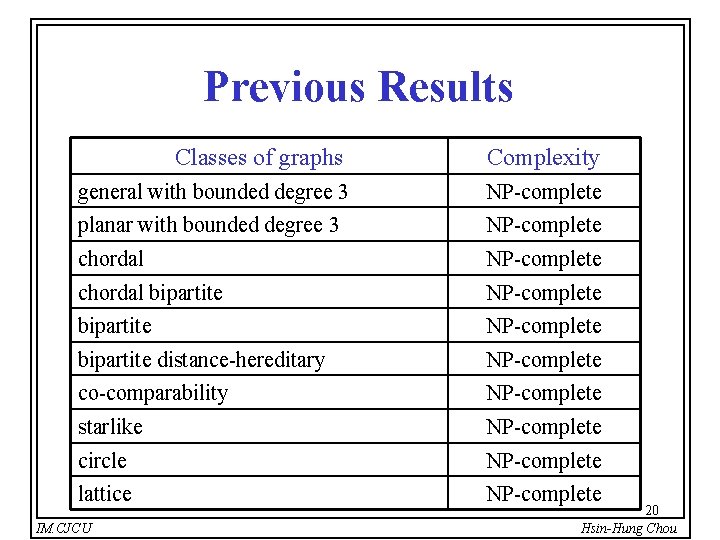
Previous Results Classes of graphs Complexity general with bounded degree 3 NP-complete planar with bounded degree 3 NP-complete chordal bipartite NP-complete bipartite distance-hereditary NP-complete co-comparability NP-complete starlike NP-complete circle NP-complete lattice NP-complete IM. CJCU 20 Hsin-Hung Chou

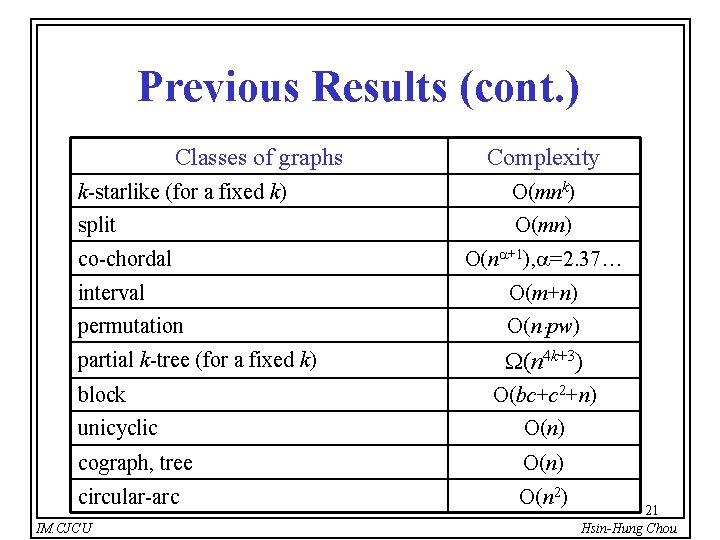
Previous Results (cont. ) Classes of graphs Complexity k-starlike (for a fixed k) O(mnk) split O(mn) co-chordal O(n +1), =2. 37… interval O(m+n) permutation O(n pw) partial k-tree (for a fixed k) (n 4 k+3) block unicyclic O(bc+c 2+n) O(n) cograph, tree O(n) circular-arc O(n 2) IM. CJCU 21 Hsin-Hung Chou

Outline • • Motivation Avenue system on trees Previous results Result on unicyclic graphs • motivation • avenue system on trees • linear-time algorithm • Conclusions IM. CJCU 22 Hsin-Hung Chou

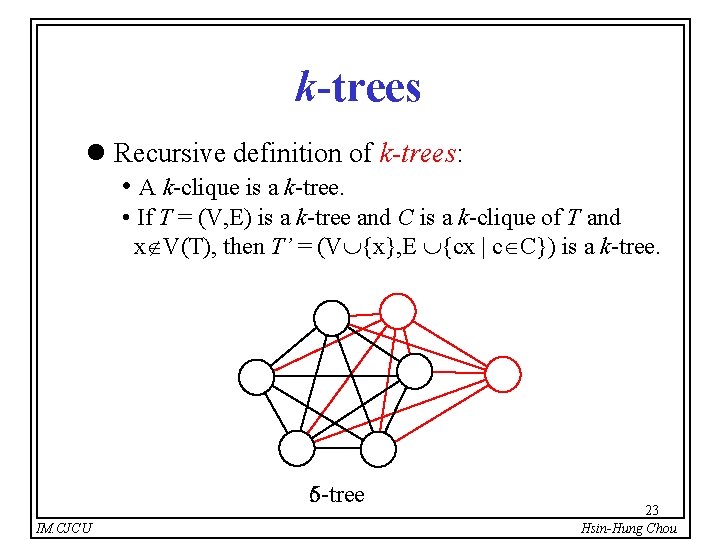
k-trees l Recursive definition of k-trees: • A k-clique is a k-tree. • If T = (V, E) is a k-tree and C is a k-clique of T and x V(T), then T’ = (V {x}, E {cx | c C}) is a k-tree. 5 -tree 6 -tree IM. CJCU 23 Hsin-Hung Chou

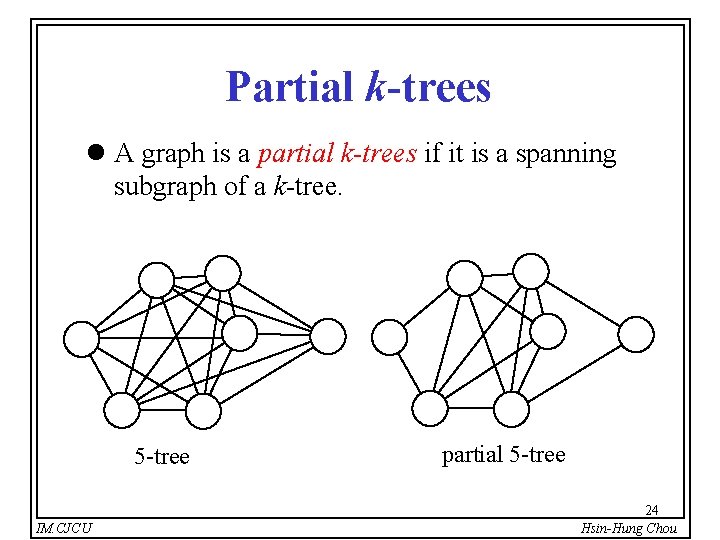
Partial k-trees l A graph is a partial k-trees if it is a spanning subgraph of a k-tree. 5 -tree IM. CJCU partial 5 -tree 24 Hsin-Hung Chou

Unicyclic Graphs l A unicyclic graph is a graph composed of a l A unicyclic graph is a partial 2 -tree with one extra edge. IM. CJCU 25 Hsin-Hung Chou

Results on Unicyclic Graphs • Hans L. Bodlaender and Ton Kloks, “Efficient and constructive algorithms for the pathwidth and treewidth of graphs”, Journal of Algorithms, 21(no. 2): pp. 358– 402, 1996. Time complexity: (n 4 k+3) for a partial k-tree with fixed k. • J. A. Ellis and M. Markov, “Computing the vertex separation of unicyclic graphs”, Information and Computation, 192: pp. 123– 161, 2004. Time complexity: O(n log n). • Our result: O(n). IM. CJCU 26 Hsin-Hung Chou

Outline • • Motivation Avenue system on trees Previous results Result on unicyclic graphs • motivation • avenue system on trees • linear-time algorithm • Conclusions IM. CJCU 27 Hsin-Hung Chou

Results on Trees • J. A. Ellis, I. H. Sudborough, and J. S. Turner, “The vertex separation and search number of a graph”, Information and Computation, 113(no. 1): pp. 50– 79, 1994. Search number: O(n); Optimal search strategy: O(n log n). • S. L. Peng, C. W. Ho, T. S. Hsu, M. T. Ko, and C. Y. Tang, “A linear-time algorithm for constructing an optimal node-search strategy of a tree”, LNCS 1449: pp. 279– 288, 1998. • K. Skodinis, “Construction of linear tree-layouts which are optimal with respect to vertex separation in linear time”, Journal of Algorithms, 47: pp. 40– 59, 2003. Optimal search strategy: O(n). IM. CJCU 28 Hsin-Hung Chou

Parsons’ Lemma l [PAR 76] For any tree T and an integer k 2, ns(T) k+1 if and only if there exists a vertex v with at least three branches having search numbers at least k. k+1 k IM. CJCU k k branch 29 Hsin-Hung Chou

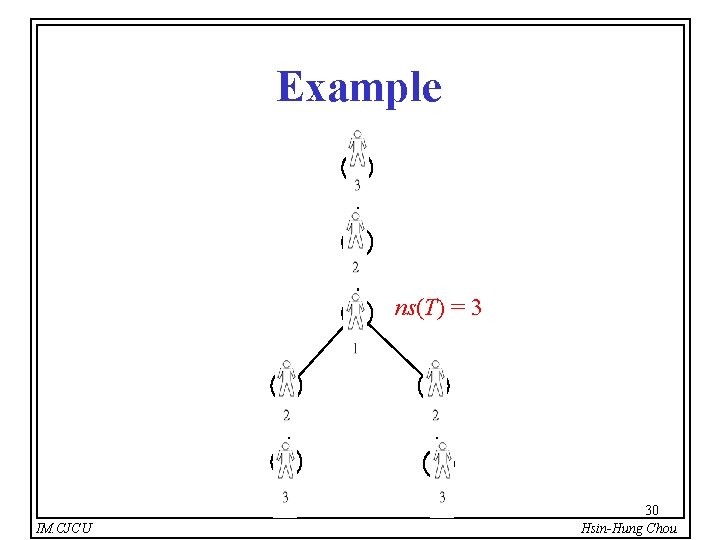
Example ns(T) = 3 IM. CJCU 30 Hsin-Hung Chou

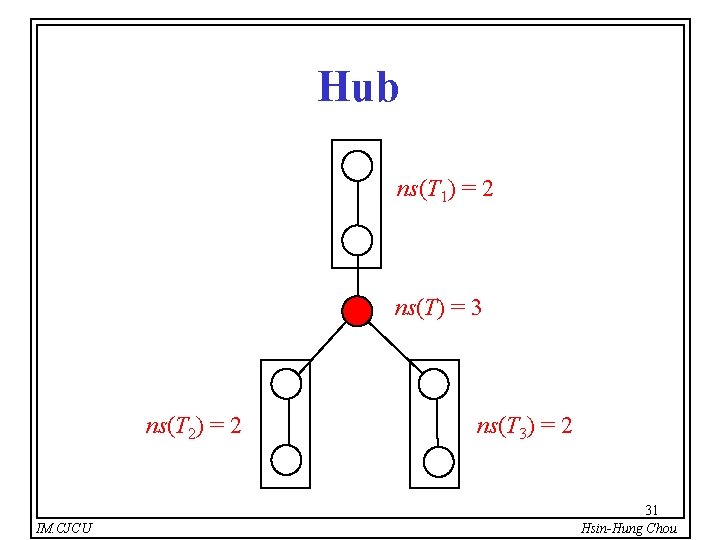
Hub ns(T 1) = 2 ns(T) = 3 ns(T 2) = 2 IM. CJCU ns(T 3) = 2 31 Hsin-Hung Chou

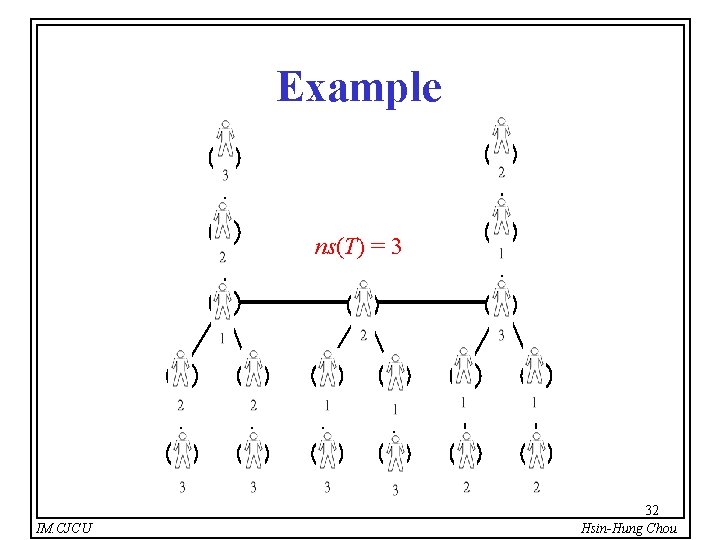
Example ns(T) = 3 IM. CJCU 32 Hsin-Hung Chou

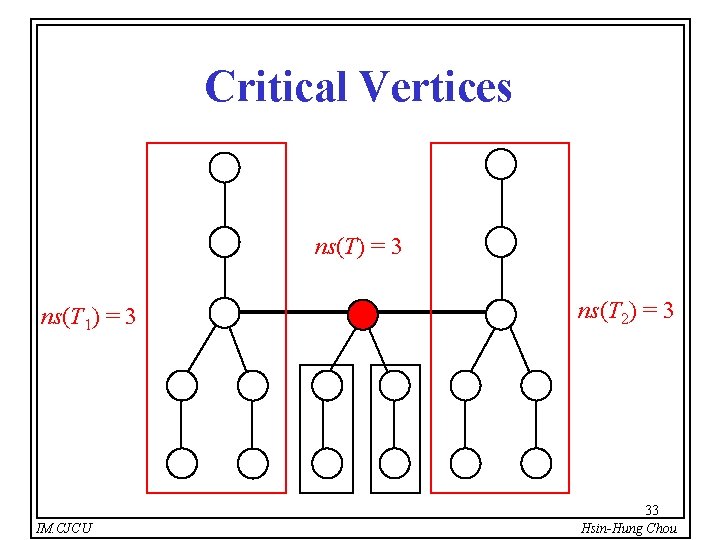
Critical Vertices ns(T) = 3 ns(T 1) = 3 IM. CJCU ns(T 2) = 3 33 Hsin-Hung Chou

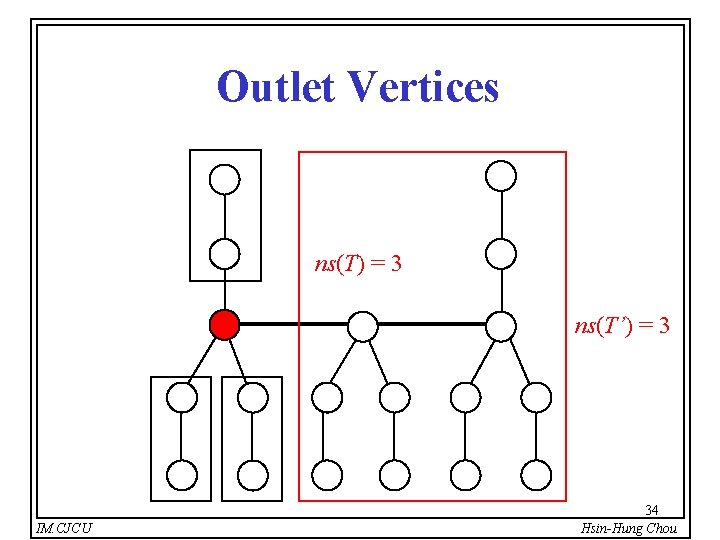
Outlet Vertices ns(T) = 3 ns(T’) = 3 IM. CJCU 34 Hsin-Hung Chou

Avenue on Trees l [MEG 88] For any tree T, a path P = [v 1, v 2, . . . , vr] is an avenue of T, if the following conditions hold: • If r = 1, then v 1 is a hub. • If r > 1, then each of v 1 and vr is an outlet vertex, and for every j, 2 j r-1, vj is a critical vertex. l [MEG 88] For any tree T, T has an avenue. If the length of the avenue is at least two, then the avenue is unique. IM. CJCU 35 Hsin-Hung Chou

Dynamic Programming • Every tree under construction has a specified vertex called the root. • The algorithm computes the search number based on the tree decomposition using dynamic programming. IM. CJCU 36 Hsin-Hung Chou

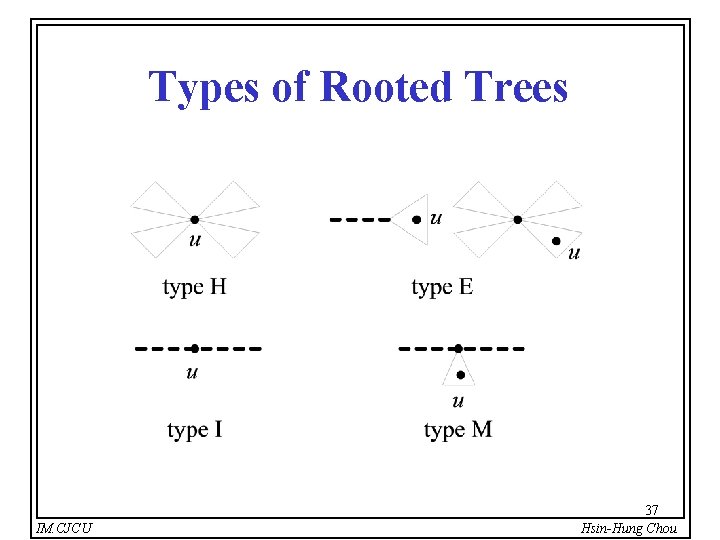
Types of Rooted Trees IM. CJCU 37 Hsin-Hung Chou

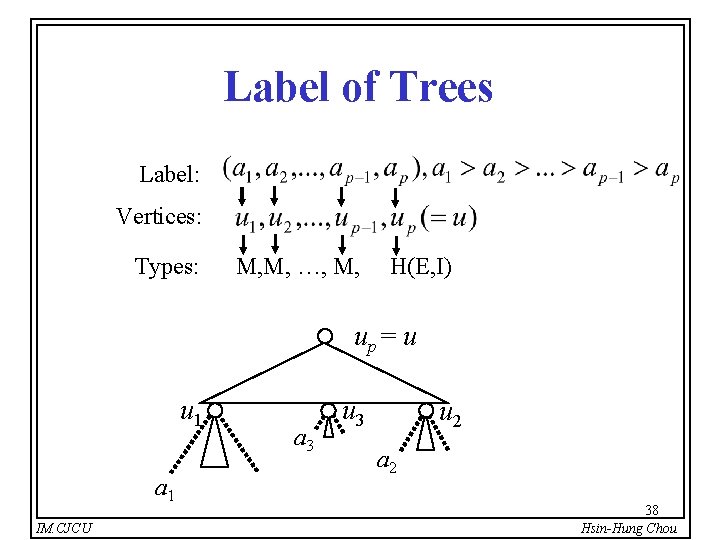
Label of Trees Label: Vertices: Types: M, M, …, M, H(E, I) up= u u 1 a 1 IM. CJCU a 3 u 2 a 2 38 Hsin-Hung Chou

Merge Rules – Case 1 • If there exist at least three labels containing k which is the maximum element in all labels, then = (k+1’) k IM. CJCU k … k 39 Hsin-Hung Chou

Merge Rules – Case 2 • If there exist exactly two labels containing k and one of them contains a k-critical vertex , then = (k+1’) k k k IM. CJCU … <k <k 40 Hsin-Hung Chou

Merge Rules – Case 3 • If there exist exactly two labels containing k and neither of them contains a k-critical vertex , then = (k) k IM. CJCU k … <k <k 41 Hsin-Hung Chou

Merge Rules – Case 4 • If there exist exactly one label containing k and it contains a k-critical vertex x, and ns(Tu[x]) = k, then = (k+1’) <k k … <k <k x k IM. CJCU 42 Hsin-Hung Chou

Merge Rules – Case 5 • If there exist exactly one label containing k and it contains a k-critical vertex x, and ns(Tu[x]) < k, then = (k)& (Tu[x]) <k k … <k <k x k IM. CJCU 43 Hsin-Hung Chou

Merge Rules – Case 6 • If there exists exactly one label containing k and it contains no k-critical vertex , then = (k’) k IM. CJCU <k … <k <k 44 Hsin-Hung Chou

Outline • • Motivation Avenue system on trees Previous results Result on unicyclic graphs • motivation • avenue system on trees • linear-time algorithm • Conclusions IM. CJCU 45 Hsin-Hung Chou

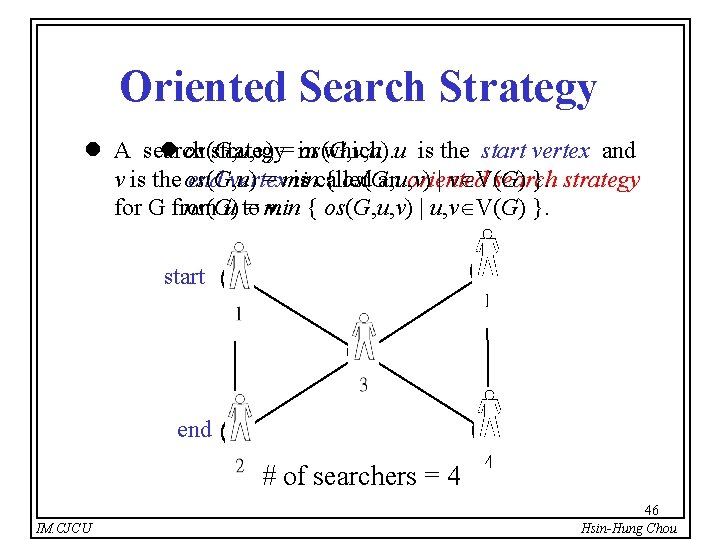
Oriented Search Strategy l A search l os(G, u, v) strategy= in os(G, v, u). which u is the start vertex and v is the os(G, u) end vertex = min is called { os(G, u, v) an oriented | v V(G) search }. strategy for G from ns(G) u to = min v. { os(G, u, v) | u, v V(G) }. start b u a end v c # of searchers = 4 IM. CJCU 46 Hsin-Hung Chou

Main Algorithm (Phase 1) • Compute the labels of rooted constituent trees. IM. CJCU 47 Hsin-Hung Chou

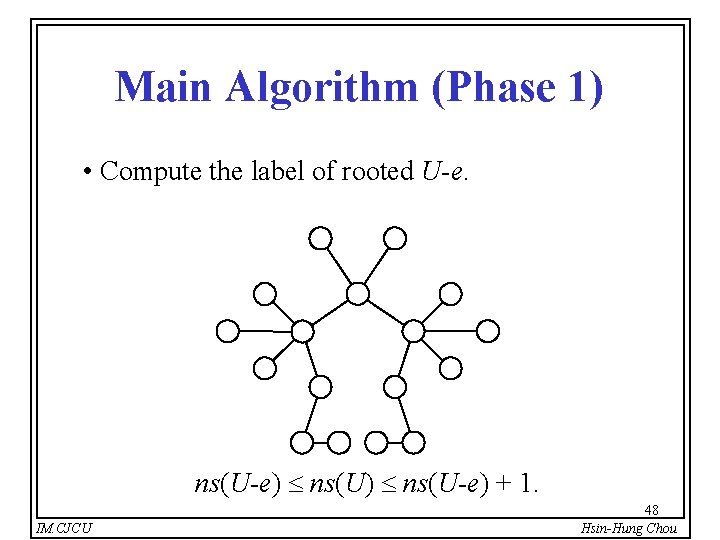
Main Algorithm (Phase 1) • Compute the label of rooted U-e. ns(U-e) + 1. IM. CJCU 48 Hsin-Hung Chou

Main Algorithm (Phase 1) • Construct the label array of U. Example: ={ 1=(9, 8, 6, 4’), 2=(8’), 3=(7, 6)}. H A [1] E I A [ 2] i n i n i ptri ni. ALL n H E I M A [3] A [4] [4, H , v 1] 4 1 1 0 0 2 0 0 1 1 4 1 0 0 0 1 6 2 0 1 7 1 0 0 0 1 8 A [5] A [6] [6, M , v 1] 3 A [7] [7, M , v 3] 1 [8, M , v 1] 2 [9, M , v 1] 1 A [8] A [9] IM. CJCU [6, I , v 3] 2 [8, E , v 2] 1 49 Hsin-Hung Chou

Main Algorithm (Phase 2) • Decide ns(U) = k or k+1, where k = ns(U-e), based on the labels of U-e and constituent trees. IM. CJCU 50 Hsin-Hung Chou

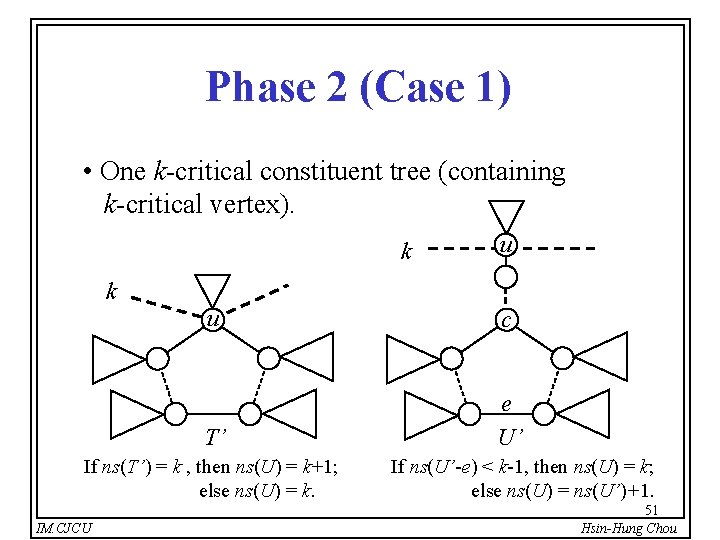
Phase 2 (Case 1) • One k-critical constituent tree (containing k-critical vertex). k k u c T’ e U’ If ns(T’) = k , then ns(U) = k+1; else ns(U) = k. IM. CJCU u If ns(U’-e) < k-1, then ns(U) = k; else ns(U) = ns(U’)+1. 51 Hsin-Hung Chou

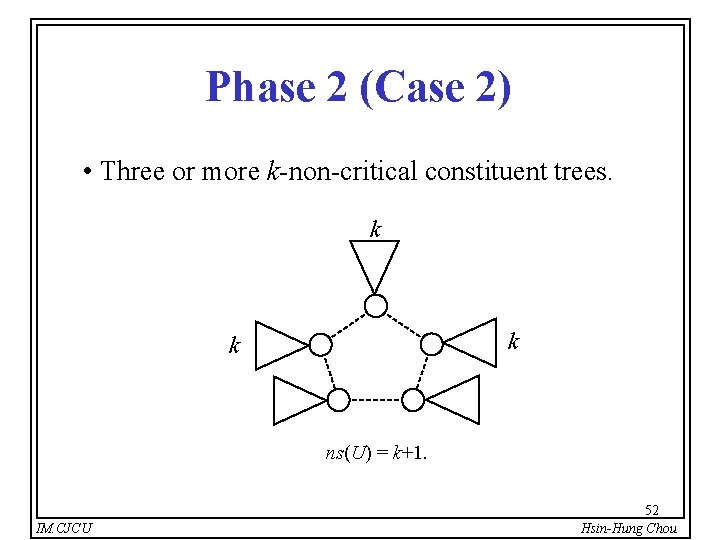
Phase 2 (Case 2) • Three or more k-non-critical constituent trees. k k k ns(U) = k+1. IM. CJCU 52 Hsin-Hung Chou

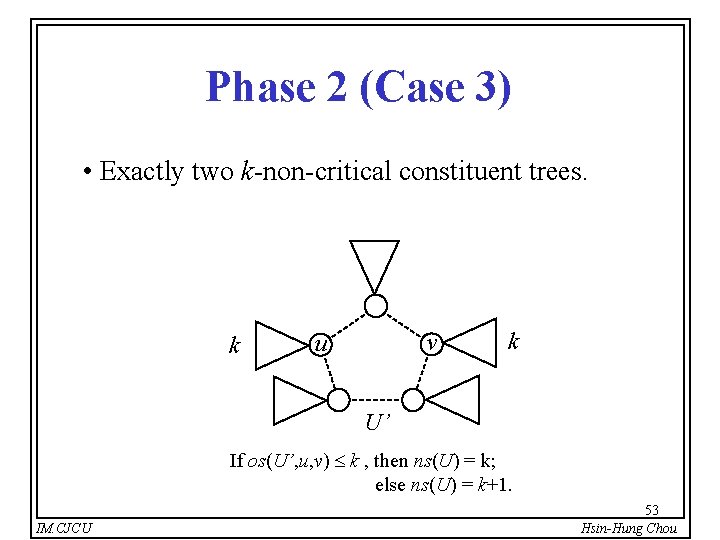
Phase 2 (Case 3) • Exactly two k-non-critical constituent trees. k v u k U’ If os(U’, u, v) k , then ns(U) = k; else ns(U) = k+1. IM. CJCU 53 Hsin-Hung Chou

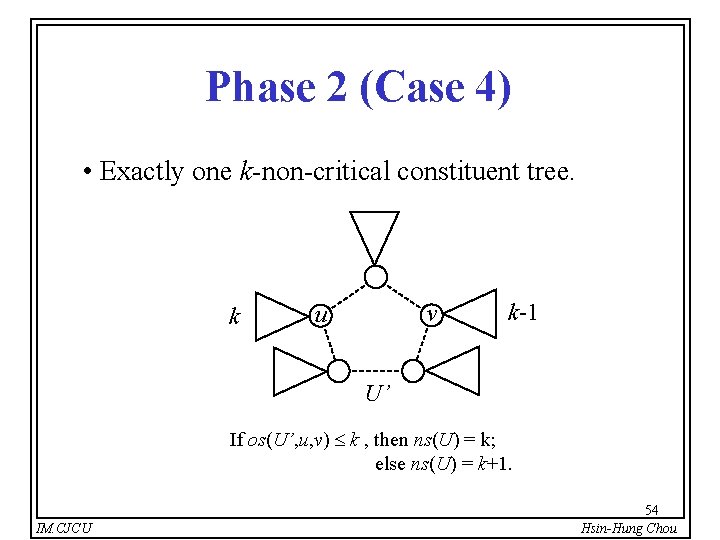
Phase 2 (Case 4) • Exactly one k-non-critical constituent tree. k v u k-1 U’ If os(U’, u, v) k , then ns(U) = k; else ns(U) = k+1. IM. CJCU 54 Hsin-Hung Chou

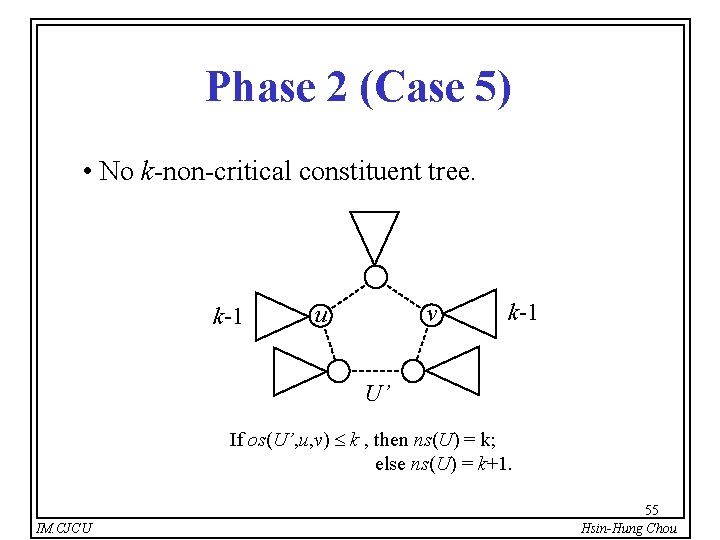
Phase 2 (Case 5) • No k-non-critical constituent tree. k-1 v u k-1 U’ If os(U’, u, v) k , then ns(U) = k; else ns(U) = k+1. IM. CJCU 55 Hsin-Hung Chou

Conclusion l Unicyclic graph: O(n). • unicyclic cactus partial k-tree (O(n 4 k+3)). l Cactus graph: IM. CJCU 56 Hsin-Hung Chou

Thank you for your attention! IM. CJCU 57 Hsin-Hung Chou

Q&A IM. CJCU 58 Hsin-Hung Chou