The Network Simplex Method Reduced Costs and Node

The Network Simplex Method Reduced Costs and Node Potentials Updated 7 April 2008 Network Simplex: Part 2

Reduced Costs: Generic Simplex Method • The row 0 coefficients of the Simplex Tableau are known as reduced costs. • The reduced cost of a basic variable is zero. • Non-basic variables with negative reduced cost are eligible to enter the basis. – If all the reduced costs are non-negative, then the Simplex method terminates. Network Simplex: Part 2 2

Formula to Compute Reduced Costs • Let B be the set of basic variables. • Let AB be the submatrix of A comprised of the columns corresponding to the basic variables. • Let c' be the vector of reduced costs (i. e. row 0 of the tableau). • c' = c – A where = c. B(AB)-1. • are referred to as the dual multipliers. Network Simplex: Part 2 3

Formula in the Network Context Network Simplex: Part 2 4

Formula in the Network Context Network Simplex: Part 2 5

Reduced Costs: Network Simplex • • Let c'ij be the reduced cost of arc (i, j) and i be the potential at node i. c'ij = cij - i + j where 1. 1 = 0 2. c'ij = 0 for all basic arcs • Eligible non-basic arcs – Arcs in L are eligible if c'ij < 0 – Arcs in U are eligible if c'ij > 0 Network Simplex: Part 2 6

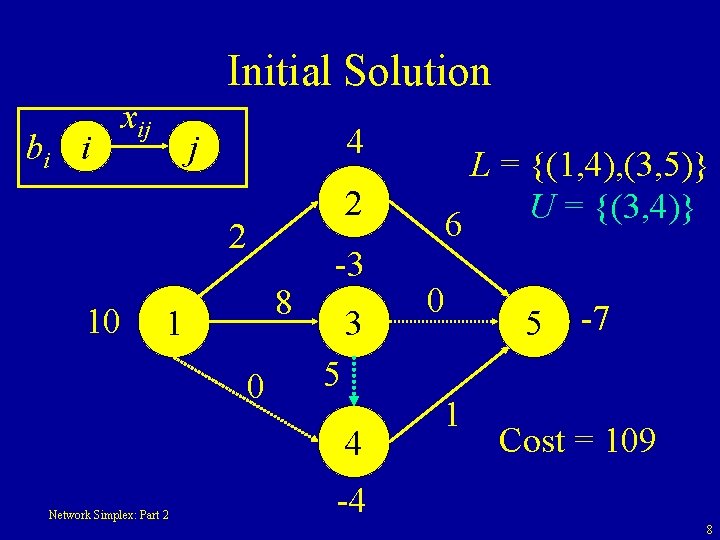
An initial BFS • Basic arcs (variables) B = {(1, 2), (1, 3), (2, 5), (4, 5)} • Non-basic arcs at their lower bounds L = {(1, 4), (3, 5)} • Non-basic arcs at their upper bounds. U = {(3, 4)} Network Simplex: Part 2 7

Initial Solution bi i xij 4 j 2 2 10 8 1 0 -3 3 5 4 Network Simplex: Part 2 L = {(1, 4), (3, 5)} U = {(3, 4)} 6 0 1 5 -7 Cost = 109 -4 8

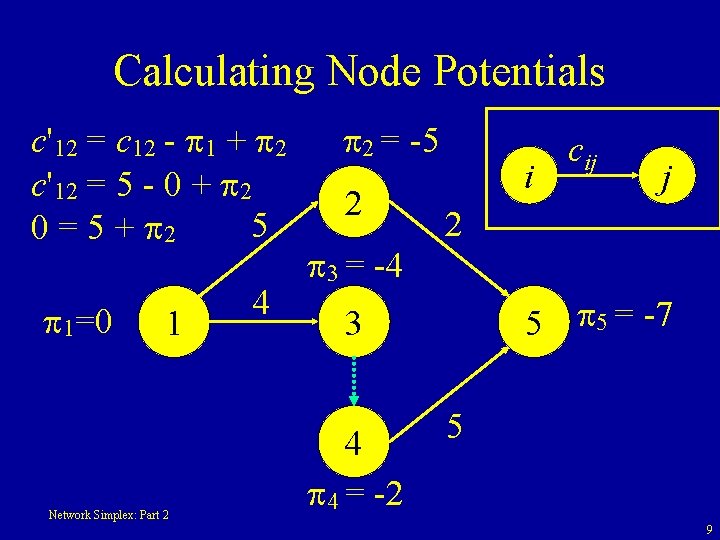
Calculating Node Potentials c'12 = c 12 - 1 + 2 c'12 = 5 - 0 + 2 5 0 = 5 + 2 1=0 1 Network Simplex: Part 2 4 2 = -5 2 3 = -4 i j 2 5 5 = -7 3 4 4 = -2 cij 5 9

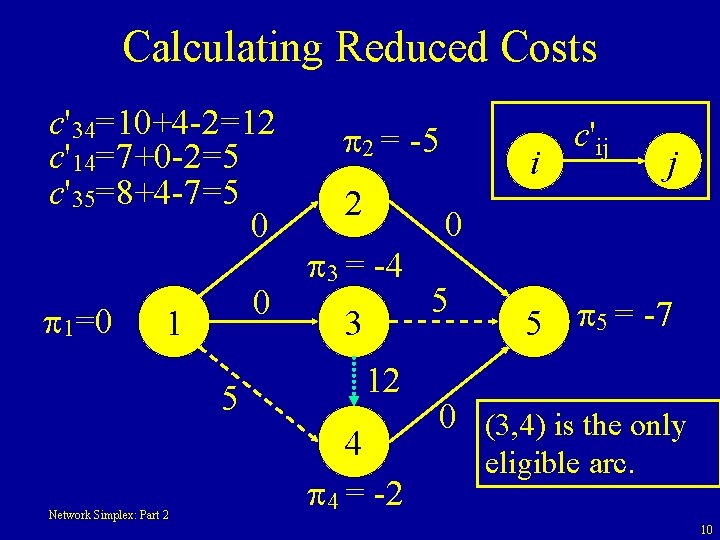
Calculating Reduced Costs c'34=10+4 -2=12 c'14=7+0 -2=5 c'35=8+4 -7=5 0 1=0 0 1 5 Network Simplex: Part 2 2 = -5 2 3 = -4 3 12 4 4 = -2 i c'ij j 0 5 5 5 = -7 0 (3, 4) is the only eligible arc. 10

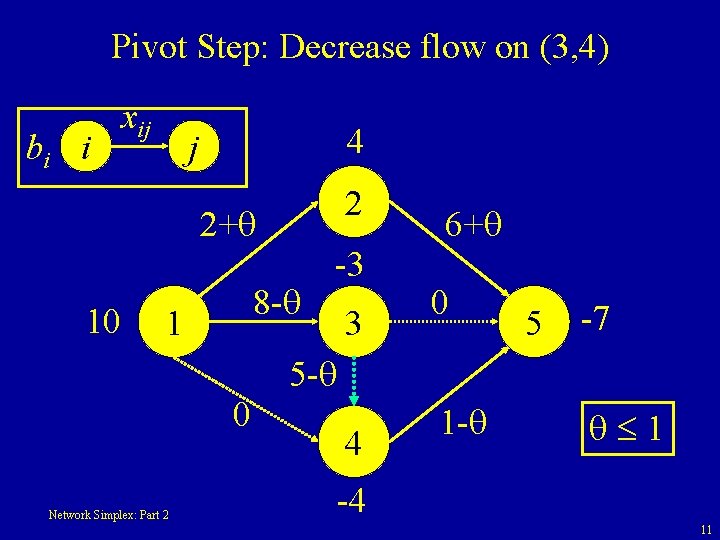
Pivot Step: Decrease flow on (3, 4) bi i xij 4 j 2 2+ 10 8 - 1 -3 3 6+ 0 5 -7 5 - 0 Network Simplex: Part 2 4 1 - 1 -4 11

Decreasing the flow on (3, 4) • Consider decreasing the flow on (3, 4) by • Cost = 109 + (-c 13 -c 34 - c 45 + c 12 + c 25) =109 + (4 -10 -5+5+2) = 109 - 12 • Maximum decrease is = 1. Flow on (4, 5) goes to 0. Network Simplex: Part 2 12

Decreasing the flow on (3, 4) • To bring arc (3, 4) in to the basis we need to reduce its flow. • The more we reduce the flow on (3, 4), the more we will improve the objective function. • To maintain flow balance, we must – Keep the flow on (1, 4) and (3, 5) at zero – Decrease flow on (1, 3) and (4, 5) – Increase flow on (1, 2) and (2, 5) • When (3, 4) becomes basic, (4, 5) will become nonbasic and join L. Network Simplex: Part 2 13

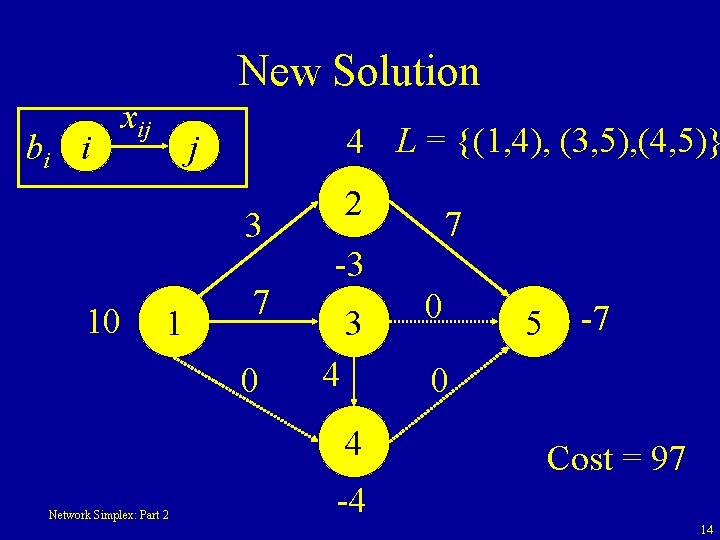
New Solution bi i xij 4 L = {(1, 4), (3, 5), (4, 5)} j 3 10 1 7 0 2 -3 3 4 0 5 -7 0 4 Network Simplex: Part 2 7 Cost = 97 -4 14

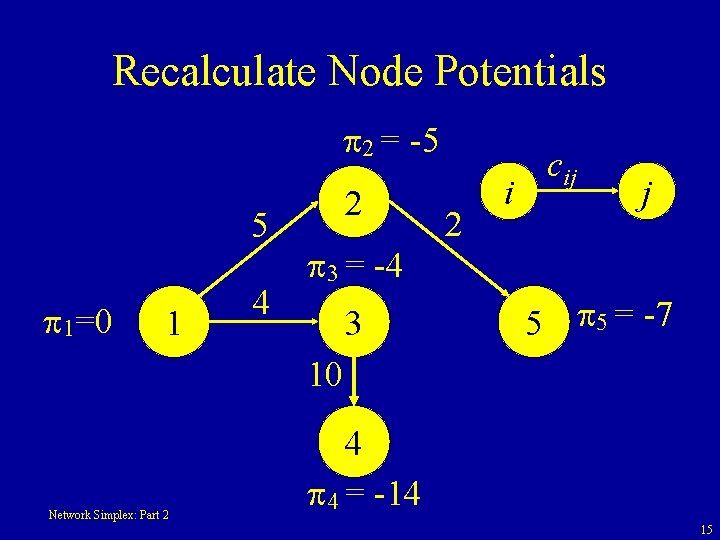
Recalculate Node Potentials 2 = -5 5 1=0 1 4 2 3 = -4 3 2 i cij j 5 5 = -7 10 Network Simplex: Part 2 4 4 = -14 15

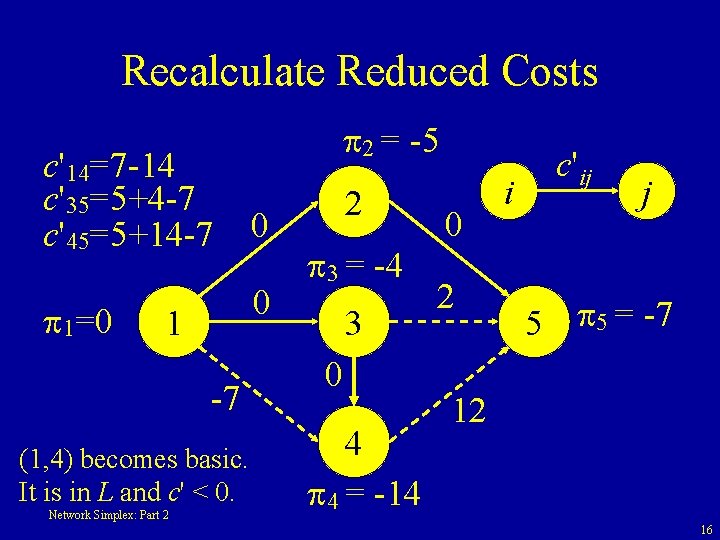
Recalculate Reduced Costs c'14=7 -14 c'35=5+4 -7 c'45=5+14 -7 1=0 0 0 1 -7 (1, 4) becomes basic. It is in L and c' < 0. Network Simplex: Part 2 2 = -5 2 3 = -4 3 0 4 4 = -14 0 2 i c'ij j 5 5 = -7 12 16

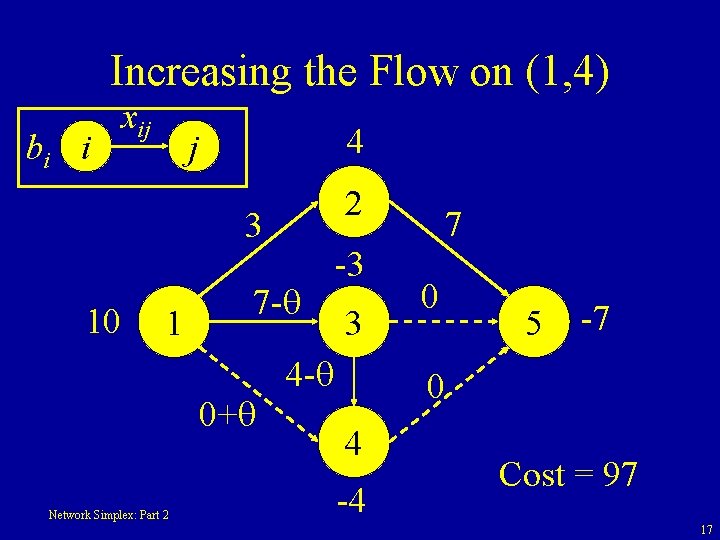
Increasing the Flow on (1, 4) bi i xij 4 j 2 3 10 1 7 - -3 3 4 - 0+ Network Simplex: Part 2 7 0 5 -7 0 4 -4 Cost = 97 17

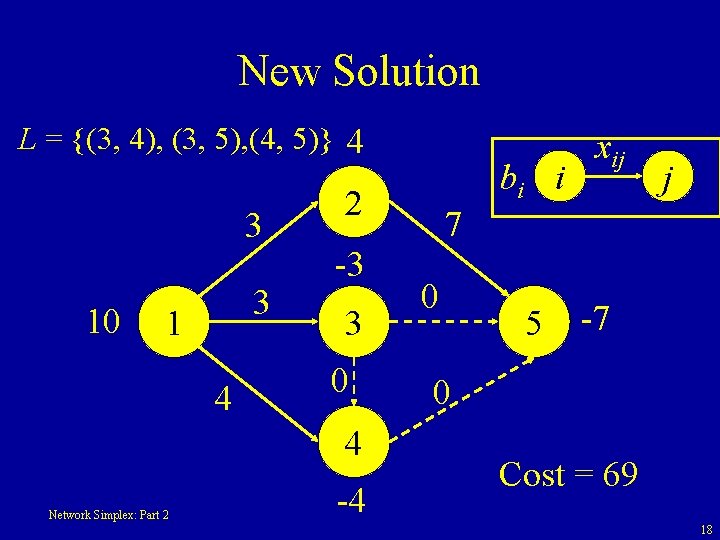
New Solution L = {(3, 4), (3, 5), (4, 5)} 4 3 10 3 1 4 2 -3 3 0 4 Network Simplex: Part 2 bi i -4 xij j 7 0 5 -7 0 Cost = 69 18

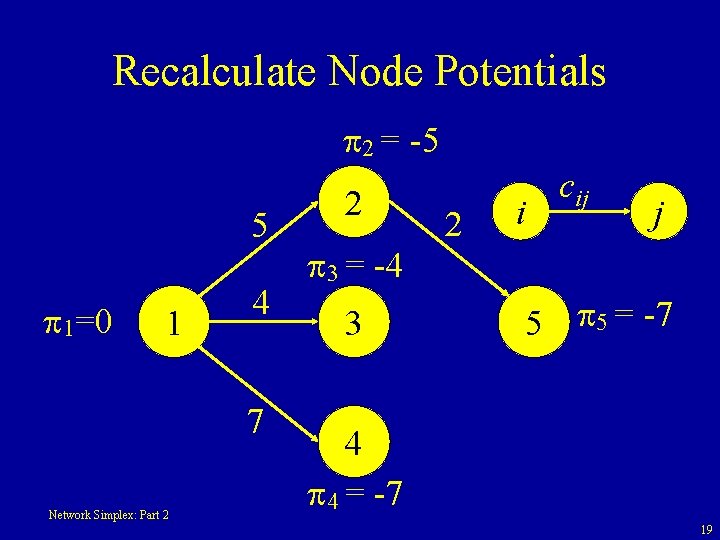
Recalculate Node Potentials 2 = -5 5 1=0 1 4 7 Network Simplex: Part 2 2 3 = -4 3 2 i cij j 5 5 = -7 4 4 = -7 19

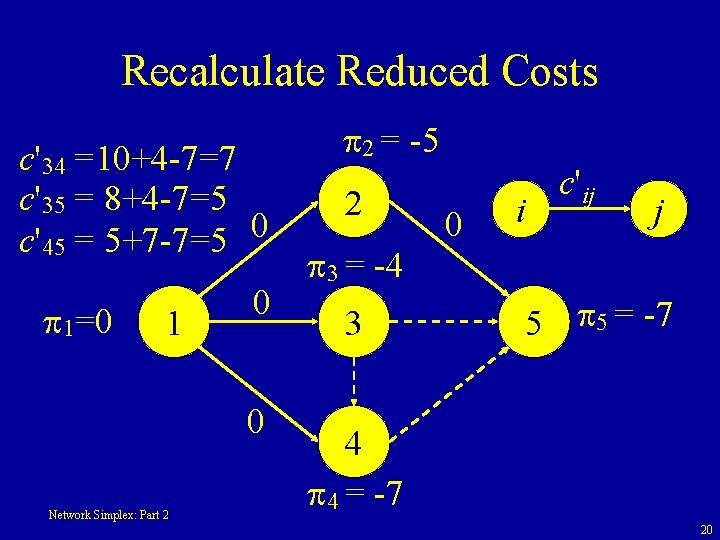
Recalculate Reduced Costs c'34 =10+4 -7=7 c'35 = 8+4 -7=5 c'45 = 5+7 -7=5 0 1=0 1 0 0 Network Simplex: Part 2 2 = -5 2 3 = -4 3 0 i c'ij j 5 5 = -7 4 4 = -7 20

Outline of Network Simplex 1. 2. 3. 4. 5. Determine a starting BFS. The n-1 basic variables correspond to a spanning tree. Compute the node potentials. Compute the reduced costs for the non-basic arcs. – The current solution is optimal if all arcs in L have non-negative reduced cost and all arcs in U have nonpositive reduced cost. Select a non-basic arc (i, j) to enter the basis. Identify the cycle created by adding (i, j) to the tree. Use flow conservation to determine the new flows on the arcs in the cycle. The arc that first hits lower or upper limit leaves the basis. Network Simplex: Part 2 21