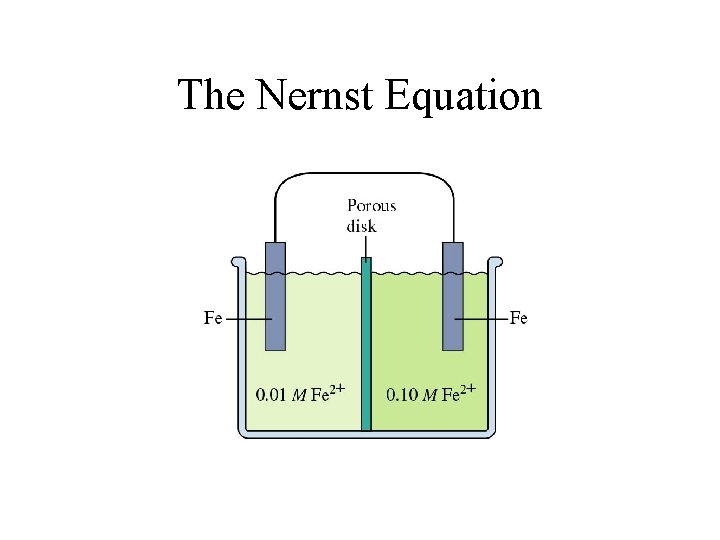
The Nernst Equation The Nernst Equation Standard potentials

The Nernst Equation

The Nernst Equation Standard potentials assume a concentration of 1 M. The Nernst equation allows us to calculate potential when the two cells are not 1. 0 M. R = 8. 31 J/(mol K) T = Temperature in K n = moles of electrons in balanced redox equation F = Faraday constant = 96, 485 coulombs/mol e-

Concentration and Ecell • At 298 K the following version can be used: Ecell = E°cell - (0. 0591/n)log(Q) The Nernst Equation

Q Q is the reaction Quotient: a. A + b. B c. C + d. D Q = [C]c [D]d [A]a [B]b not liquids or solids

Concentration and Ecell • With the Nernst Eq. , we can determine the effect of concentration on cell potentials. Ecell = E°cell - (0. 0591/n)log(Q) • Example. Calculate the cell potential for the following: Fe(s) + Cu 2+(aq) Fe 2+(aq) + Cu(s) Where [Cu 2+] = 0. 3 M and [Fe 2+] = 0. 1 M

Concentration and Ecell (cont. ) • First, need to identify the two half reacions Fe(s) + Cu 2+(aq) + 2 e- Fe(s) + Cu 2+(aq) Fe 2+(aq) + Cu(s) Fe 2+(aq) + 2 e- E° 1/2 = 0. 34 V E° 1/2 = +0. 44 V Fe 2+(aq) + Cu(s) E°cell = +0. 78 V

Concentration and Ecell (cont. ) • Now, calculate Ecell Fe(s) + Cu 2+(aq) Fe 2+(aq) + Cu(s) E°cell = +0. 78 V Ecell = E°cell - (0. 0591/n)log(Q) Ecell = 0. 78 V - (0. 0591 /2)log(0. 33) Ecell = 0. 78 V - (-0. 014 V) = 0. 794 V

Determining Concentration • If [Cu 2+] = 0. 3 M, what [Fe 2+] is needed so that Ecell = 0. 76 V? Fe(s) + Cu 2+(aq) Fe 2+(aq) + Cu(s) E°cell = +0. 78 V Ecell = E°cell - (0. 0591/n)log(Q) 0. 76 V = 0. 78 V - (0. 0591/2)log(Q) 0. 02 V = (0. 0591/2)log(Q) 0. 676 = log(Q) 4. 7 = Q

Concentration and Ecell (cont. ) Fe(s) + Cu 2+(aq) Fe 2+(aq) + Cu(s) 4. 7 = Q [Fe 2+] = 1. 4 M

Calculating Gibbs free energy and the equilibrium constant from the cell potential

Equilibrium Constants and Cell Potential At equilibrium, equilibrium forward and reverse reactions occur at equal rates, therefore: 1. The battery is “dead” 2. The cell potential, E, is zero volts Modifying the Nernst Equation (at 25 C):

Calculating an Equilibrium Constant from a Cell Potential Zn + Cu 2+ Zn 2+ + Cu E 0 = + 1. 10 V

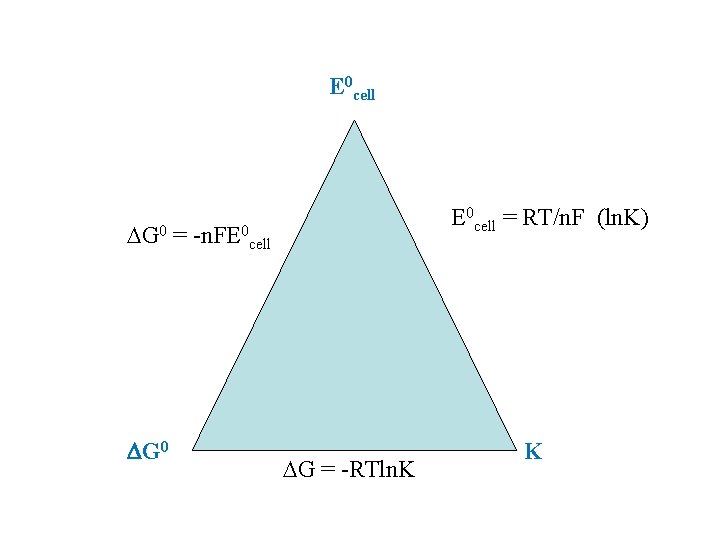
Calculating 0 G for a Cell G 0 = -n. FE 0 n = moles of electrons in balanced redox equation F = Faraday constant = 96, 485 coulombs/mol e- Zn + Cu 2+ Zn 2+ + Cu E 0 = + 1. 10 V

E 0 cell = RT/n. F (ln. K) G 0 = -n. FE 0 cell DG 0 G = -RTln. K K