The Nature of Reality and Quantum Mechanics I

The Nature of Reality and Quantum Mechanics

“I think it is safe to say that no one understands quantum mechanics. Do not keep saying to yourself, if you can possibly avoid it, “But how can it be like that ? ”, because you will go “down the drain” into a blind alley from which nobody has yet escaped. Nobody knows how it can be like that. " Richard Feynman

“A player put a ball on the table and hit it with the cue. Watching the rolling ball, Mr. Tompkins noticed to his great surprise that the ball began to "spread out. " This was the only expression he could find for the strange behavior of the ball which, moving across the green field, seemed to become more and more washed out, losing its sharp contours. It looked as if not one ball was rolling across the table but a great number of balls, all partially penetrating into each other. Mr. Tompkins had often observed analogous phenomena before, but today he had not taken a single drop of whiskey and he could not understand why it was happening now. ” George Gamow, Mr. Tompkins in Wonderland

QM Example We have teams of horses and cows together, and we wish to separate the cows. We pass them through a gate that allows only horses. Then we want to separate the white horses from the rest, so we pass them through another gate admitting only white horses. We are surprised that our final sample consists of white horses and a few cows! [TUNNELING EFFECT]

IN QUANTUM MECHANICS: Ax. B Bx. A

John Bell Thought Experiment Take a coin and split it into two discs, one containing “head”; the other “tail”. Give it to two individuals who do not see the pieces and let them travel far apart. Now when one looks at his half coin and finds it is “head”, he knows at once that the other must be “tail”, even if the other person (or anyone else) has not looked at it yet. This is so because the pieces carry information and they are correlated from the start – we just did not know it. Again when on the way, before looking at any piece, the probability of a piece to be head or tail is 50%. Now when the first person looks and it is “head”, for him the probability that the other coin is “tail” is 100%, but for the other person carrying it, it is still 50%! The difference of this coin experiment and QM is that in QM even after the first person saw that he had “head” he cannot assume that the other piece is “tail” until the other person has seen the second piece (or some one)! In QM until a measurement is made there is no reality. But what constitutes a measurement?

Wave-Particle Duality: Light WAVE

Wave-Particle Duality: Light PARTICLE (Photon)

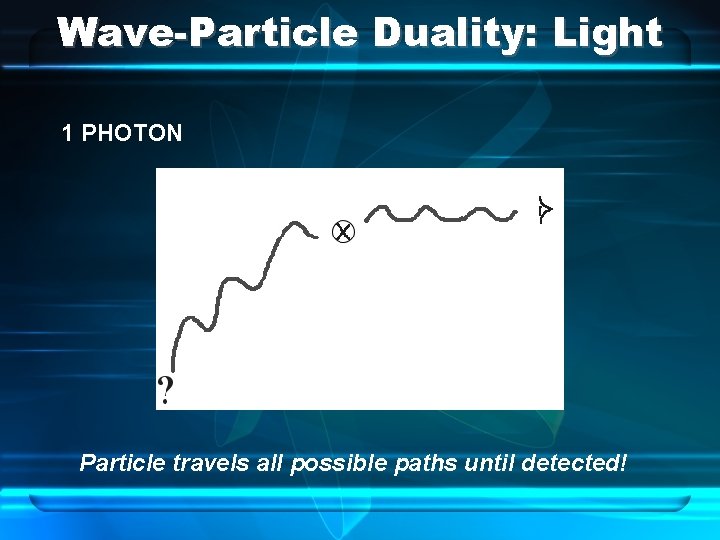
Wave-Particle Duality: Light 1 PHOTON Particle travels all possible paths until detected!

Ocean Waves

Double slit interference

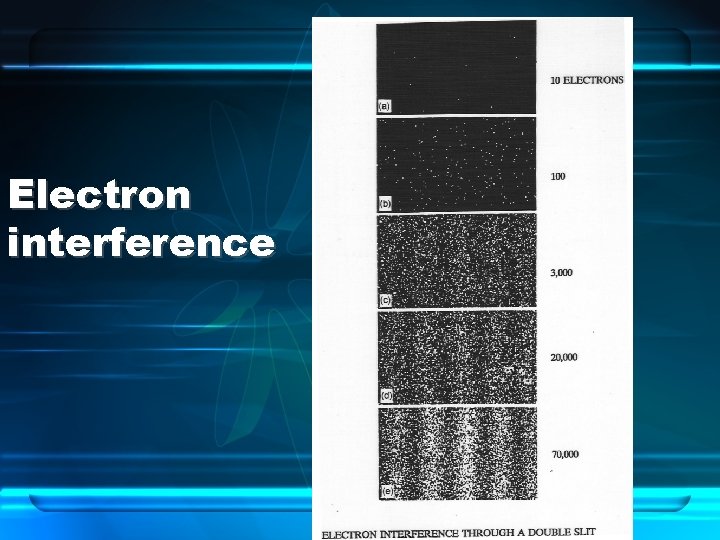
Electron interference

Our common sense picture of the world demands that a single, indivisible photon can only go through one of two slits – it cannot be in two places at the same time. Yet the experimental results clearly demonstrate that the photon acts as if it can go through both slits and be in two places at the same time. An interference pattern is an expression of a process that is built up from waves that are coming from two distinct directions. But how is this possible when only a single, indivisible photon is involved? Look at the experiment in a different way, and suppose that one of the slits is closed. Using a normal beam of light, interference is no longer possible, and the pattern vanishes. But when it comes to a single photon, this should not matter. A photon is indivisible; it can only go through one of two slits. If it passes through slit A, for example, why should it matter whether slit B is open or closed? Nevertheless, it does matter. When slit B is closed, the quantum-interference pattern vanishes; when slit B is open, this pattern reappears. But how can this be? How can a photon passing through slit A know whether slit B is open or closed? In passing through one part of the screen, how can it know what is happening in some other part?

Could the photon somehow split itself in two, so that half a photon goes through slit A and half through slit B? No, photons are by their very nature indivisible, so they cannot split in half. The inevitable conclusion is that quantum theory has thrown commonsense out of the window and that physicists have been forced to acknowledge that single, indivisible photons act as if they can pass through two slits at once and be in two places at the same time. Either that, or some new and mysterious communication is taking place that seems to inform a photon in one part of the universe what is happening in other parts. PARTICLES OR WAVES?

Quantum Mechanics • Science is a kind of honesty – wanting to know what is really going on. • When it comes to the meaning of QM and reality – we seem to be lost and do not understand what is going on. Yet physicists almost never discuss this topic! • One of the best kept secrets is that physicists have lost their grip on reality. • The reason is QM! (History 1925, Bohr, Heisenberg, Schrödinger, etc. ) • QM is a mathematical recipe to make predictions. QM works, even when we do not understand it! • Neils Bohr had a horseshoe on his house door – one of his students once asked him “surely you are not superstitious? ” “ No, no” said Bohr, “but they say that it brings luck even if you do not believe in it. ”

QM : What Meaning? • • QM shows that there is no deep reality. There is no reality without observation. The measurement makes reality. The universe would not exist if we had not evolved on Earth to observe it! (The Anthropic Principle). We do not know what is holding the pyramid of science up!

“YOU NEVER KNOW WHERE YOU’RE GOING UNTIL YOU GET THERE. ” Yogi Berra

Interpretation of Quantum Mechanics Baseball Example 1. I calls’em like I see’em. 2. I calls’em they way they are. 3. They ain’t nothin’ till I calls’em.

Interpretation of Quantum Mechanics Baseball Example 1. I calls’em like I see’em. 2. I calls’em they way they are. 3. They ain’t nothin’ till I calls’em. 1. Subjective (Unreliable) 2. Einstein’s Interpretation (Realism) 3. Bohr’s Interpretation

Copenhagen Interpretation The Measurement Makes Reality • • • A cat is enclosed in a chamber with a canister of poison gas. The canister is connected to some apparatus that can detect the up or down spin of a particle. If the spin is up, a level is activated which breaks the canister and the cat dies of poisoning. If the spin is down, the cat lives. Now the spin of a particle is undetermined until it is measured (up and down are equally probable). A particle is injected and interacts with the apparatus – until we open the chamber we do not know if the cat is alive or dead. Copenhagen interpretation implies that until an observer opened the chamber to see whether or not the cat was poisoned, the animal could not be considered to be either dead or alive. Until an observation was made the quantum states “cat alive” and “cat dead” existed with equal probability. Only when the experimenter looked at the cat one or the other state assumed “objective reality”. For some this is absurd! (A half-dead / half-alive cat).

“Schrödinger’s Cat’s a mystery cat, He illustrates the laws; The complicated things he does have no apparent cause; He baffles the determinist, and drives him to despair; For when they try to pin him down – the quantum cat’s not there!” T. S Eliot “Old Possum’s Book of Practical Cats”

A PROBLEM What is a measurement? Who is the measurer?

Wave-Particle Duality Louis de Brogile h/p p = momentum = mv From: E = mc 2 E = hc / = h / mv (mass has a “wavelength”)

Wave Mechanics Wave equation, oscillations in 3 dimensions:

Schrödinger’s Equation

Time Dependent Schrödinger Wave Equation

Particle-Momentum Commutation

The Uncertainty Principle (or the incompleteness theorem) • The position and momentum (mass x velocity) of a particle cannot be measured simultaneously with arbitrary accuracy. • The more accurately the position is determined, the less we can tell about the particle’s momentum. • And if the momentum is found with great precision, then the particle’s position is relatively unknown! PUZZLE One can choose to measure either position or momentum. It appears that the experimenter’s choice determines what properties a particle can have.

Physics of the Microcosm Quantum Mechanics The Uncertainty Principle Quantities cannot be known with unrestricted accuracy. If x = uncertainty in position p = uncertainty in momentum, (p=mv) Then x • p > h / 2 Also, t = least length of time to make a measurement E = accuracy of measured energy t • E > h / 2 Fundamental limits to the precision with which we can know nature.

Heisenberg’s Uncertainty Principle If we measure p of a 200 gm baseball traveling at 40 m / sec (4000 cm / sec) to an accuracy of 0. 1 percent (0. 001 p), what is the fundamental limit of the precision to which we can measure its position? x • p > h / 2 x > h / 2 p p = mv = 200 gm x 4000 cm/sec = 8 x 105 gm cm/sec p = 0. 001 p = 8 x 102 gm cm/sec x > (6. 6 x 10 -27 erg sec) / (2 x 8 x 102 gm cm/sec) = 1. 3 x 10 -30 cm For macroscopic objects the result is too small to measure.

Same problem for an electron (e- mass = 9. 1 x 10 -28 gm) with a velocity 106 m/sec (108 cm/sec) x > 12 cm ! Many times the size of an atom! We have to settle for much less precision in the e- momentum to localize its position on an atomic scale.

QM and Atoms • Bohr atom has exact electron orbits (or energy levels. • In QM the energy levels are probabilistic. High probabilities agree with the Bohr atom. High probability of finding the e- Low probability of finding the e-

THE UNCERTAINTY PRINCIPLE IS A CERTAINTY PRINCIPLE

“IS THE MOON THERE WHEN NOBODY LOOKS? ” Quantum Mechanics • Physical properties have no objective reality independent of the act of observation. • Observations not only disturb what has to be measured they produce it. • (Try to observe the position of an e- how? With a beam of light? But photons bouncing from the ewill change the position!) Albert Einstein • Albert did not agree. He wanted things to have properties whether or not they were measured.

QM only gives the probability of an event QM does not give a deterministic statement that an event will happen or not. • The probability of finding a particle at a certain location is a spread out function (say an e- around the nucleus of an atom). • Now, when a measurement is made, the particle is eithere or not there. If it is there, did the particle have that position all along, before the measurement was made? – QM: Not sure, until it was measured. – Einstein: • Yes, except that it was unknown to the experimenter. • QM is incomplete, something is missing to provide determinism.

“I’d rather be clear and wrong, than foggy and right. ” -Einstein

EPR Einstein, Podolosky, and Rosen, 1935 • Thought experiment to demonstrate the incompleteness of QM. • Such experiments were made possible after 1964, when John Bell described a quantitative method to test QM.

EPR Paradox • Experiment involves two electrons • Before being measured, each electron has an equal probability of spinning up or down. QM says the spin is indeterminate. Each electron acquires a definite spin (up or down) only upon the act of measurement. • Suppose we have two electrons with a total spin of zero, that is one electron will have spin “up” and the other will have spin “down”. • The two electrons drift away from each other (very far apart). • If we measure the spin of one electron, and find it was “down”, we immediately know the spin of the other electron, which should be “up” – even though that second electron has not been measured yet (and its spin should be indeterminate according to QM)! • PARADOX? Information cannot travel faster than the speed of light. But clearly measuring one electron has affected the other instantaneously. “Spooky action at a distance. ” How does the second electron know what happened to the first?

The Nature of Reality (I) • Science is only a method – – Observations Hypothesis Verification Law THE SCIENTIFIC METHOD • The success of this method depends on the degree of predictive power. • This method deals only with empirical phenomena – those that can be observed and measured. • The success of the scientific method has created the notion that nature is DETERMINISTIC – that is related to a “cause and effect” principle. • In the macroscopic world this causality principle works very well.

The Nature of Reality (II) • Using the same scientific method QUANTUM MECHANICS was developed to explain the behavior of the microscopic world – the world of the atom. • QM provided predictions in terms of probabilities, and introduced the “uncertainty principle”. • For a single atomic measurement predictions are more probabilistic (and less deterministic). However, as we move from a few atomic particles to multiparticle systems, quantum mechanical probabilities approach classical determinism (Decoherence). • QM predicts the position of an e- in an atom with say 50% accuracy, but can predict the position of a rocket around the moon with extremely high accuracy. • QM is the best theory we have today. It is the most successful theory which gives the most accurate predictions.

Local realistic theories of nature (I) Assumptions 1. Realism: Regularities in observed phenomena are caused by some physical reality that is independent of human beings. 2. Induction: Conclusions can be made by consistent observations. 1. Separability (or Locality): No influence can propagate faster than the speed of light.

Local Realistic Theories of Nature (II) Assumption are regarded as self-evident – Realism – Induction – Separability • Following local realistic theories we can make predictions about the results of experiments dealing with atoms. • QM can also be used to make predictions of the same experiments. • Surprisingly, the two predictions do not agree! • Hence, either QM is wrong (or incomplete), or the assumption(s) of the local realistic theories are wrong. • Recent experiments (A. Aspect, France) show that the results are consistent with theory of quantum mechanics.

Psychology Test Example (An Analogy) • Give a test to all people (Pass/Fail) – Results are mixed – not sure if they measure some property. (REALISM, results independent of experimenter). • Analyze sub-set of married couples. – Results are mixed again. – But when husband passes, so does the wife and vice versa. (During the test husband wife do note communicate – SEPARABILITY). • Therefore, if correlations persist, we are measuring some fixed and not random property, which existed BEFORE the test. • If the sample is representative, then we can infer that this property exists in the untested population (INDUCTION). Above sample is based on the local realistic theories. QM, however, argues: Results show no predictable correlations until they are measured. That is fixed properties did not exist before the measurements were made.

QM or Local Realistic Theories? Can we make an actual experiment to decide? In 1964, John Bell described mathematically how an experiment can be performed (Bell’s Inequality). – Take atomic particles with 3 stable properties: A, B, C Each property has 2 values: A+, A-, B+, B-, C+, C-. – Bell computed the combination of probabilities and deduced “Bell’s Inequality”, assuming local realistic theories. – Now we can make measurements and test Bell’s Theorem. If we get agreement then QM is wrong. ACUTAL EXPERIMENT – Alain Aspect (France) Experiment Bell’s Theorem is not obeyed, Quantum Mechanics Wins!

Bell’s Gedanken Experiment (David Mermin, Physics Today, 1985) Apparatus: – Two detectors far apart – “A” and “B” – Each detector has a switch with 3 settings – 1, 2, 3 – Each detector responds to an event by flashing a light (GREEN or RED) – A Source of particles (Say Photons) is placed at the center. There are no connections between any of the pieces.

Experiment 1. Set detectors A and B INDEPENDENTLY and RANDOMLY to one of the 3 settings. 2. Push button on the source, so particles will be emitted and travel to the detectors to be measured. 3. When they are detected either the RED or the GREEN light will go on for each detector. 4. Record the settings and colors of each detector for every measurement, and repeat many times. EXAMPLE OF A RECORD Detector: A B Position Set at: 3 2 Light Flashed RED GREEN READ: 32 RG

OUTPUT

Results 1. If we examine all runs, they all occur with equal frequency (any run is equally likely). 2. If we examine only those runs when the switches had the same settings, then one finds that the lights always flash the same colors. (11 GG, 22 RR, 33 RR, ETC. ) Should we be bothered by such data? How does detector “A” know what color to flash when the switches for both detectors are set at the same position and “B” flashes red – if there are no possible connections between “A” and “B”? • Particles carry instructions! Not possible, because result (1) above would not be true. Therefore, no instructions. • “Spooky action at a distance” (Albert) • As close to magic as anything • The moon is not there when no one looks!

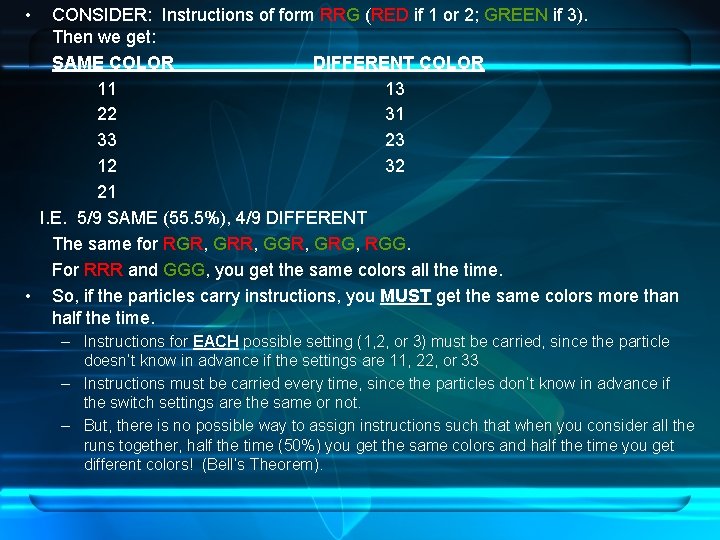
Conclusion • Regardless of how instructions are chosen, when one examines all the results we must find that the same color flashed > 55. 5% of the time. • This conclusion is known as “Bell’s Inequality”. • But the real experiment shows the same colors flash only 50% of the time. The experiment violates Bell’s Inequality, but Bell’s Inequality is based on the existence of instruction sets. • Therefore, no instruction sets exist. But, if no instructions, then how do we always get the same colors when the switches are the same? [Experiment with photons passing through three polarized disks, photons will either pass or be blocked. ]

• CONSIDER: Instructions of form RRG (RED if 1 or 2; GREEN if 3). Then we get: SAME COLOR DIFFERENT COLOR 11 13 22 31 33 23 12 32 21 I. E. 5/9 SAME (55. 5%), 4/9 DIFFERENT The same for RGR, GRR, GGR, GRG, RGG. For RRR and GGG, you get the same colors all the time. • So, if the particles carry instructions, you MUST get the same colors more than half the time. – Instructions for EACH possible setting (1, 2, or 3) must be carried, since the particle doesn’t know in advance if the settings are 11, 22, or 33 – Instructions must be carried every time, since the particles don’t know in advance if the switch settings are the same or not. – But, there is no possible way to assign instructions such that when you consider all the runs together, half the time (50%) you get the same colors and half the time you get different colors! (Bell’s Theorem).

Instructions? • Consider particles carry instructions when they leave the source – such as – “Flash” R if your switch is set to 1, R if set to 2, and G if set to 3. – or instruction RRG • There are eight possible instruction sets: RRR RRG RGR RGG GRR GRG GGR GGG

Bell’s Inequality • Altogethere are nine different possible pairs of the switches: 11, 12, 13, 21, 22, 23, 31, 32, 33 Each of which appears as often as any other in a long set of experiments. • For the colors the possibilities are: RR, RG, GR, GG Each of which appears as often as any other in a long set of experiments Results 1. When the switches have the same setting, the lights always flash the same color. 2. In all the runs (regardless of how the switches were set), the same colors flash as often as different colors (RR or GG 50% of all runs). Random colors in all runs; only the same colors when the switches are the same. There are no connections between detectors, nor between detectors and source.

Alternative • THERE IS NO PARADOX • THAT’S THE WAY NATURE IS • EVERYTHING IS INTERRELATED

FUTURE GTR ? ? QUANTUM GRAVITY QM MODIFY? GTR? QM?

“I cannot define the real problem. Therefore, I suggest there’s no real problem, But I’m not sure There’s no real problem. ” R. Feynman