The Multiplication Principle Permutations Finite 8 1 A

The Multiplication Principle: Permutations Finite 8 -1

• A restaurant offers the following menu: Main Course Vegetables Beverage Beef Potatoes Milk Ham Green Beans Coffee If you must choose 1 main course, 1 vegetable, and 1 beverage, in how many ways can you order a meal? Counting

1. If a process can be broken down into two steps, performed in order, with n 1 ways of completing the first step and n 2 ways of completing the second step after the first step is completed, then there are n 1 • n 2 ways of completing the process. 2. More generally, if a process can be understood as a sequence of k steps performed in order, with ni the possible number of ways of completing the i-th step after the first i-1 steps have been completed, then the number of ways of completing the process is the product n 1 • n 2 • • • nk. The Multiplication Principle:

• Outcome – The result of a trial • Sample Space – All possible outcomes • Event – One or more outcome Counting Principle - Definitions

Counting Principle

Counting Principle

Counting Priciple

Counting Priciple

Counting Principle

32 Counting Principle

Counting Principle

• For the breakfast special at the Fronii diner, customers can choose their eggs scrambled, fried, or poached, whole wheat or white toast, and either orange, apple tomato or grapefruit juice. • How many different breakfast specials can a customer order? 24 ways Counting Principle

• Independent events – Events that do not affect the choice of another event • Dependent events – The outcome of one event does affect the outcome of another event Counting Principle - Definitions

Counting Principle

• Independent Events – Examples – Rolling a dice – Flipping a coin • Dependent Events – Examples – Picking a name from a hat (not replacing) – Toppings on a pizza (unless you can double up) – Ways things are arranged Counting Principle

• The guests at a sleepover brought 8 DVD’s. They decided they would watch only 3 movies. How many orders of 3 different movies are possible? 8 * 7 * 6 = 336 Counting Principle

• How many ways can the first five letters of the alphabet be arranged if each letter is used only once? 5 * 4 * 3 * 2 * 1 = 120 Counting Principle

• How many different ways can four different books be arranged on a shelf? 4 * 3 * 2 * 1 = 60 Counting Principle

• The top 5 runners at the cross country meet will receive trophies. If there are 22 runners in the race, in how many ways can the trophies be awarded? 22 * 21 * 20 * 19 * 18 = 3, 160, 080 Counting Principle

Practice Problems

Practice Problems

Practice Problems

Practice Problems

Practice Problems

Permutations

• Permutation – When items are arranged in a certain order Permutations

Number of Permutations of n Distinct Objects taken r at a time: N objects are distinct Once used an object cannot be repeated Order is important n! n. Pr = -----(n – r)! Permutations without replacement

Permutations

• From a list of 20 books, each student must choose 4 books for book reports. The first report is a traditional book report, the second is a poster, the third a newspaper interview with one of the characters, and the fourth a timeline of the plot. How many different orderings of books can be chosen? Permutations

• From a list of 20 books, each student must choose 4 books for book reports. The first report is a traditional book report, the second is a poster, the third a newspaper interview with one of the characters, and the fourth a timeline of the plot. How many different orderings of books can be chosen? Permutations

• From a list of 20 books, each student must choose 4 books for book reports. The first report is a traditional book report, the second is a poster, the third a newspaper interview with one of the characters, and the fourth a timeline of the plot. How many different orderings of books can be chosen? Permutations

• From a list of 20 books, each student must choose 4 books for book reports. The first report is a traditional book report, the second is a poster, the third a newspaper interview with one of the characters, and the fourth a timeline of the plot. How many different orderings of books can be chosen? Permutations

In a horse racing “Trifecta”, a gambler must pick which horse comes in first, which second, and which third. If there are 8 horses in the race, and every order of finish is equally likely, what is the chance that any ticket is a winning ticket? The probability that any one ticket is a winning ticket is 1 out of 8 P 3, or 1 out of 336 Example

Number of Permutations of n Distinct Items taken r at a time with replacement: N objects are distinct Once used an object can be repeated (replacement) Order is important P = nr Permutations with replacement

Suppose a computer requires 8 characters for a password. The first character must be a letter, but the remaining seven characters can be either a letter or a digit (0 thru 9). The password is not case-sensitive. How many passwords are possible on this computer? 26 • 367 = 2. 037 x 1012 Example

• How many ways can first and second place be awarded to ten people? 90 Permutations

Permutations

• How many different ways can the letters of the word BANANA be arranged? Calculate the total number of ways 6 letters can be arranged (6!), then divide out the times where the same letter is repeated, i. e. 3 “A” and 2 “B”, so divide by 3! and 2! 60 Permutations

• How many different ways can the letters of the word STEREO be arranged? 360 Permutations

• 3 letters, 2 digits – Steps: • Pick first letter, Pick second letter, Pick third letter, Pick first digit, Pick second digit – The number of ways depends on whether repetitions are allowed: • 26*26*26*10*10 (repetitions allowed) • 26*25*24*10*9 (no repetitions allowed) License Plates

• 6 person committee, 3 positions: chair, secretary, treasurer (A, B, C, D, E, and F) – Procedure: • Step 1. Chair • Step 2. Secretary • Step 3. Treasurer – Counting: • Step 1. 6 possibilities • Step 2. 5 possibilities • Step 3. 4 possibilities – 6*5*4 = 120 Committee Assignments

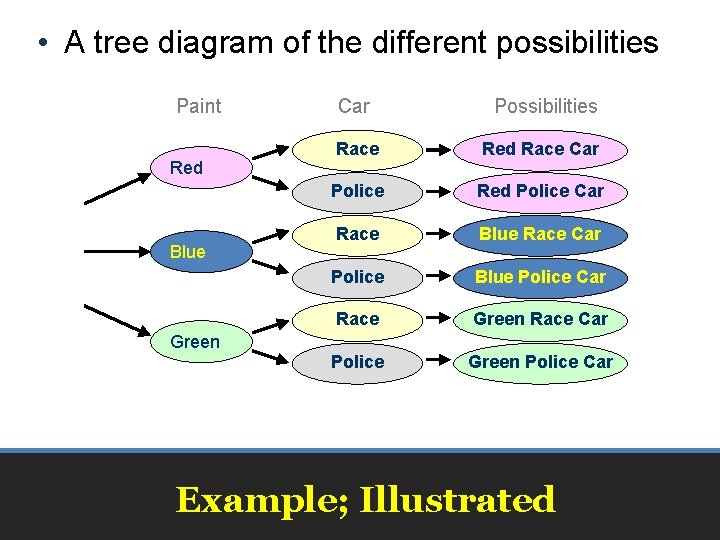
If there are 3 different colors of paint (red, blue, green) that can be used to paint 2 different types of toy cars (race car, police car), then how many different toys can there be? Example

• A tree diagram of the different possibilities Paint Red Blue Green Car Possibilities Race Red Race Car Police Red Police Car Race Blue Race Car Police Blue Police Car Race Green Race Car Police Green Police Car Example; Illustrated

Number of Permutations with Non-distinct Items: N objects are not distinct K different groups n! P = ----------- where n = n 1 + n 2 + … + nk n 1!∙n 2!∙ …. ∙nk! Permutations – non-distinct items

How many different vertical arrangements are there of 9 flags if 4 are white, 3 are blue and 2 are red? 9! 9 • 8 • 7 • 6 • 5 • 4! 9 • 8 • 7 • 6 • 5 ----------- = 1260 4! • 3! • 2! 3 • 2 • 1 Example

Homework