The Multiple Regression Model Two Explanatory Variables yt

The Multiple Regression Model

Two Explanatory Variables yt = 1 + 2 xt 2 + 3 xt 3 + εt xt affect yt separately yt = 2 xt 2 yt = 3 xt 3 But least squares estimation of 2 now depends upon both xt 2 and xt 3.

Correlated Variables yt = 1 + 2 xt 2 + 3 xt 3 + εt yt = output xt 2 = capital xt 3 = labor Always 5 workers per machine. If number of workers per machine is never varied, it becomes impossible to tell if the machines or the workers are responsible for changes in output.

The General Model yt = 1 + 2 xt 2 + 3 xt 3 +. . . + Kxt. K + εt The parameter 1 is the intercept (constant) term. The variable attached to 1 is xt 1= 1. Usually, the number of explanatory variables is said to be K 1 (ignoring xt 1= 1), while the number of parameters is K. (Namely: 1. . . K).

Statistical Properties of εt 1. E(εt) = 0 2 2. var(εt) = cov εt , εs = for t s 2 4. εt ~ N(0, )

Statistical Properties of yt 1. E (yt) = 1 + 2 xt 2 +. . . + Kxt. K 2. var(yt) = var(εt) = 2 cov(yt , ys) = cov(εt , εs)= 0 t s 4. yt ~ N( 1+ 2 xt 2 +. . . + Kxt. K, 2)

Assumptions 1. yt = 1 + 2 xt 2 +. . . + Kxt. K + εt 2. E (yt) = 1 + 2 xt 2 +. . . + Kxt. K 2 3. var(yt) = var(εt) = cov(yt , ys) = cov(εt , εs) = 0 t s 5. The values of xtk are not random 6. yt ~ N( 1+ 2 xt 2 +. . . + Kxt. K, 2 )

Least Squares Estimation yt = 1 + 2 xt 2 + 3 xt 3 + εt T S S( 1, 2, 3) = yt 1 2 xt 2 3 xt 3 t=1 Define: y*t = yt y x*t 2 = xt 2 x 2 x*t 3 = xt 3 x 3

Least Squares Estimators b 1 = y – b 2 x 2 – b 3 x 3 b 2 = b 3 = 2 * y*x* t 2 xt 3 t 2 * x y*x* t t 3 t 2 * x* y x t t 3 t 2 t 3 2 2 * * * x x x t 3 t 2 t 3 2 * x* * x y t 2 2 * x t 2 t * x* x t 2 t 3 t 2 2 2 * * * x x x t 3 t 2 t 3

Dangers of Extrapolation Statistical models generally are good only within the relevant range. This means that extending them to extreme data values outside the range of the original data often leads to poor and sometimes ridiculous results. If height is normally distributed and the normal ranges from minus infinity to plus infinity, pity the man minus three feet tall.

Interpretation of Coefficients Øbj represents an estimate of the mean change in y responding to a one-unit change in xj when all other independent variables are held constant. Hence, bj is called the partial coefficient. ØNote that regression analysis cannot be interpreted as a procedure for establishing a cause-and-effect relationship between variables.

Universal Set x 2 / x 3 x 2 x 3 B x 3 / x 2

Error Variance Estimation Unbiased estimator of the error variance: ^2 = ^ ε t Transform to a chi-square distribution: ^ 2

Gauss-Markov Theorem Under the first of five assumptions of the multiple regression model, the ordinary least squares estimators have the smallest variance of all linear and unbiased estimators. This means that the least squares estimators are the Best Linear U nbiased Estimators (BLUE).

Variances yt = 1 + 2 xt 2 + 3 xt 3 + εt var(b 2) = var(b 3) = 2 (1 r 23) 2 (xt 2 x 2) 2 (1 r 23) where r 23 = When r 23 = 0 these reduce to the simple regression formulas. 2 2 (xt 3 x 3) 2 (xt 2 x 2)(xt 3 x 3) (xt 2 x 2) (xt 3 x 3) 2 2

Variance Decomposition The variance of an estimator is smaller when: 1. The error variance, , is smaller: 2 2. The sample size, T, is larger: 2 0. T (xt 2 x 2) t=1 3. The variable values are more spread out: 2 . 2 (xt 2 x 2). 2 4. The correlation is close to zero: r 23 0.

Covariances yt = 1 + 2 xt 2 + 3 xt 3 + εt cov(b 2, b 3) = r 23 2 (1 r 23) where r 23 = 2 (xt 2 x 2) (xt 3 x 3) 2 2 (xt 2 x 2)(xt 3 x 3) (xt 2 x 2) (xt 3 x 3) 2 2

Covariance Decomposition The covariance between any two estimators is larger in absolute value when: 1. The error variance, , is larger. 2 2. The sample size, T, is smaller. 3. The values of the variables are less spread out. 4. The correlation, r 23, is high.

Var-Cov Matrix yt = 1 + 2 xt 2 + 3 xt 3 + εt The least squares estimators b 1, b 2, and b 3 have covariance matrix: var(b 1) cov(b 1, b 2) cov(b 1, b 3) cov(b 1, b 2, b 3) = cov(b 1, b 2) var(b 2) cov(b 2, b 3) cov(b 1, b 3) cov(b 2, b 3) var(b 3)

Normal yt = 1 + 2 x 2 t + 3 x 3 t +. . . + Kx. Kt + εt yt ~N ( 1 + 2 x 2 t + 3 x 3 t +. . . + Kx. Kt), 2 This implies and is implied by: εt ~ N(0, ) 2 Since bk is a linear function of the yt: bk ~ N k, var(bk) bk k z = ~ N(0, 1) var(bk) for k = 1, 2, . . . , K

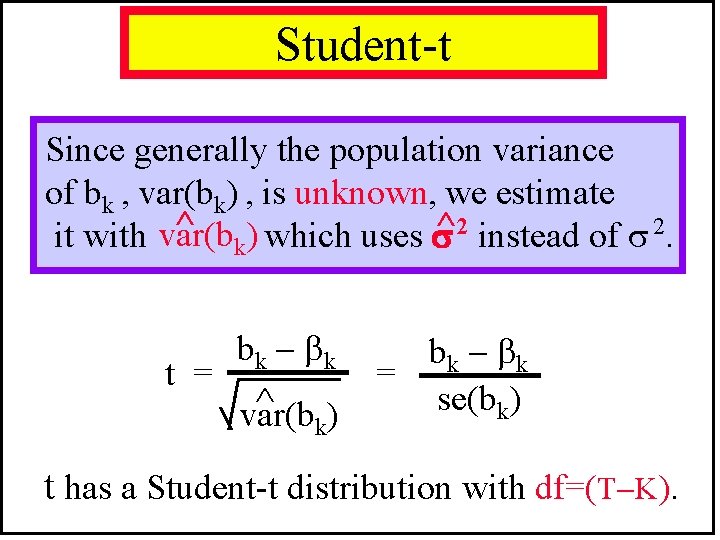
Student-t Since generally the population variance of bk , var(bk) , is unknown, we estimate ^ k) which uses ^2 instead of 2. it with var(b t = bk k ^ ) var(b k bk k = se(bk) t has a Student-t distribution with df=(T K).

Interval Estimation bk k P tc < < tc = 1 se(bk) tc is critical value for (T-K) degrees of freedom such that P( t > tc ) = /2. P bk tc se(bk) < k < bk + tc se(bk) Interval endpoints: = 1 bk tc se(bk) , bk + tc se(bk)

Student - t Test yt = 1 + 2 Xt 2 + 3 Xt 3 + 4 Xt 4 + εt Student-t tests can be used to test any linear combination of the regression coefficients: H 0: 1 = 0 H 0: 2 + 3 + 4 = 1 H 0: 3 2 7 3 = 21 H 0: 2 3 < 5 Every such t-test has exactly T K degrees of freedom where K = # of coefficients estimated(including the intercept).

One Tail Test yt = 1 + 2 Xt 2 + 3 Xt 3 + 4 Xt 4 + εt H 0: 3 < 0 H 1: 3 > 0 b 3 ~ t (T K ) t= se(b 3) df = T K = T 4 0 tc

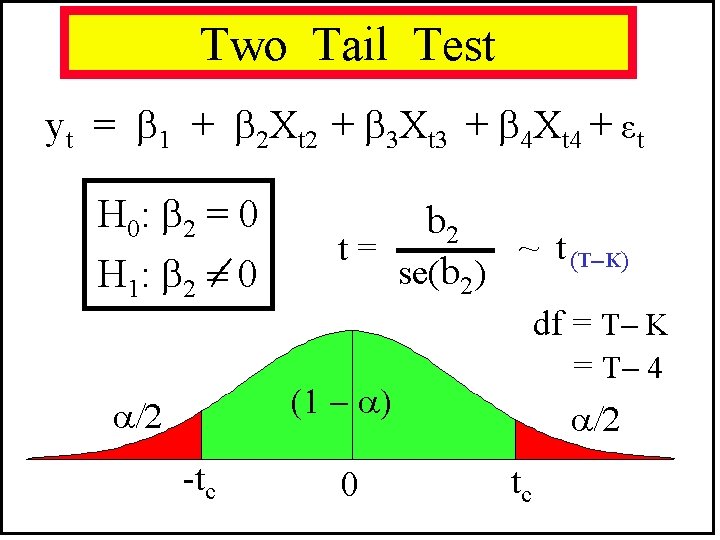
Two Tail Test yt = 1 + 2 Xt 2 + 3 Xt 3 + 4 Xt 4 + εt H 0: 2 = 0 H 1: 2 0 b 2 ~ t (T K ) t= se(b 2) df = T K = T 4 -tc 0 tc

Goodness - of - Fit Coefficient of Determination T 2 R = 2 SSR = SST 0< R <1 ^ (yt y) 2 t=1 T (yt y) t=1 2

Adjusted R-Squared Adjusted Coefficient of Determination Original: 2 R = SSR SST = 1 SSE SST Adjusted: 2 R = 1 SSE/(T K) SST/(T 1)

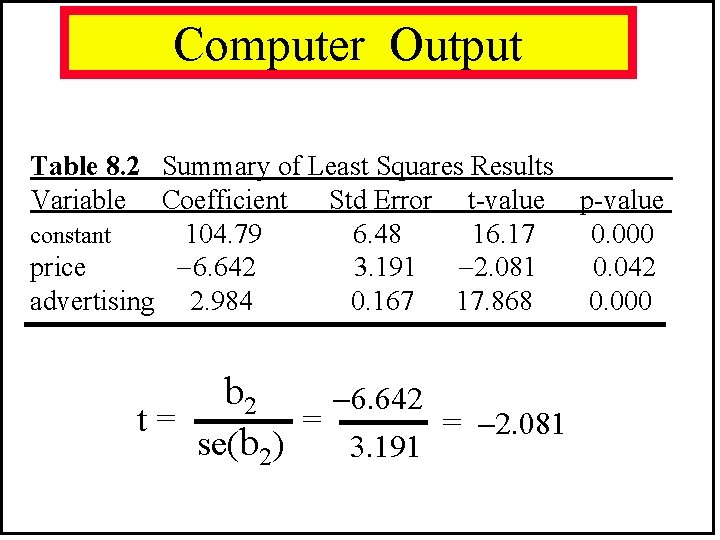
Computer Output Table 8. 2 Summary of Least Squares Results Variable Coefficient Std Error t-value p-value constant 104. 79 6. 48 16. 17 0. 000 price 6. 642 3. 191 2. 081 0. 042 advertising 2. 984 0. 167 17. 868 0. 000 b 2 6. 642 t= = = se(b 2) 3. 191 2. 081

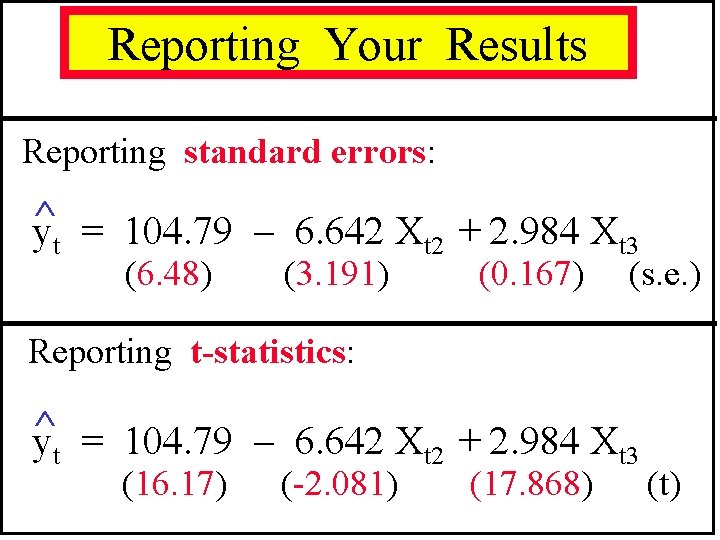
Reporting Your Results Reporting standard errors: ^ yt = Xt 2 + Xt 3 (6. 48) (3. 191) (0. 167) (s. e. ) Reporting t-statistics: ^ yt = Xt 2 + Xt 3 (16. 17) (-2. 081) (17. 868) (t)

yt = 1 + 2 Xt 2 + 3 Xt 3 + 4 Xt 4 + εt H 0: 2 = 0 H 1: 2 = 0 H 0: yt = 1 + 3 Xt 3 + 4 Xt 4 + εt H 1: yt = 1 + 2 Xt 2 + 3 Xt 3 + 4 Xt 4 + εt H 0: Restricted Model H 1: Unrestricted Model

Single Restriction F-Test yt = 1 + 2 Xt 2 + 3 Xt 3 + 4 Xt 4 + εt (SSER SSEU)/J Under H 0 F = ~ F J, T-K SSEU/(T K) = (1964. 758 1805. 168)/1 1805. 168/(52 3) = 4. 33 H 0: 2 = 0 H 1: 2 = 0 dfn = J = 1 dfd = T K = 49 By definition this is the t-statistic squared: t = 2. 081 F = t 2 =

yt = 1 + 2 Xt 2 + 3 Xt 3 + 4 Xt 4 + εt H 0: 2 = 0, 4 = 0 H 1: H 0 not true H 0: yt = 1 + 3 Xt 3 + εt H 1: yt = 1 + 2 Xt 2 + 3 Xt 3 + 4 Xt 4 + εt H 0: Restricted Model H 1: Unrestricted Model

Multiple Restriction F-Test yt = 1 + 2 Xt 2 + 3 Xt 3 + 4 Xt 4 + εt H 0: 2 = 0, 4 = 0 H 1: H 0 not true (SSER SSEU)/J F = SSEU/(T K) Under H 0 ~ F J, T-K First run the restricted dfn = J = 2 regression by dropping (J: The number of hypothesis) Xt 2 and Xt 4 to get SSER. dfd = T K = 49 Next run unrestricted regression to get SSEU.

F-Tests of this type are always right-tailed, even for left-sided or two-sided hypotheses, f(F) because any deviation from the null will make the F value bigger (move rightward). F = 0 Fc (SSER SSEU)/J SSEU/(T K) ~ F J, T-K F

F-Test of Entire Equation yt = 1 + 2 Xt 2 + 3 Xt 3 + εt We ignore 1. Why? (SSER SSEU)/J F = SSEU/(T K) H 0: 2 = 3 = 0 H 1: H 0 not true dfn = J = 2 (13581. 35 1805. 168)/2 dfd = T K = 49 = 1805. 168/(52 3) = 0. 05 = 159. 828 Reject H 0! F 2, 49, 0. 005 = 3. 187

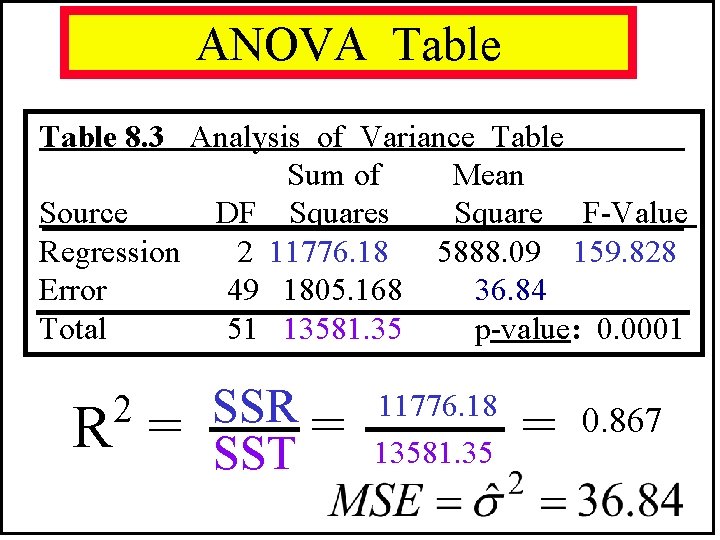
ANOVA Table 8. 3 Analysis of Variance Table Sum of Mean Source DF Squares Square F-Value Regression 2 11776. 18 5888. 09 159. 828 Error 49 1805. 168 36. 84 Total 51 13581. 35 p-value: 0. 0001 2 R = SST 11776. 18 13581. 35 = 0. 867

Nonsample Information A certain production process is known to be Cobb-Douglas with constant returns to scale. ln(yt) = 1 + 2 ln(Xt 2) + 3 ln(Xt 3) + 4 ln(Xt 4) + εt 4 = (1 2 3) where 2 + 3 + 4 = 1 ln(yt /Xt 4) = 1 + 2 ln(Xt 2/Xt 4) + 3 ln(Xt 3 /Xt 4) + εt y*t = 1 + 2 X*t 2 + 3 Xt 3* + 4 Xt 4* + εt Run least squares on the transformed model. Interpret coefficients same as in original model.

Collinear Variables The term independent variables means an explanatory variable is independent of of the error term, but not necessarily independent of other explanatory variables. Since economists typically have no control over the implicit experimental design, explanatory variables tend to move together which often makes sorting out their separate influences rather problematic.

Effects of Collinearity A high degree of collinearity will produce: 1. no least squares output when collinearity is exact. 2. large standard errors and wide confidence intervals. 2 3. insignificant t-values even with high R and a significant F-value. 4. estimates sensitive to deletion or addition of a few observations or insignificant variables. 5. The OLS estimators retain all their desired properties (BLUE and consistency), but the problem is that the influential procedure may be uninformative.

Identifying Collinearity Evidence of high collinearity include: 1. a high pairwise correlation between two explanatory variables (greater than. 8 or. 9). 2. a high R-squared (called Rj 2) when regressing one explanatory variable (Xj) on the other explanatory variables. Variance inflation factor (VIF): VIF (bj) = 1 / (1 Rj 2) ( > 10) 2 3. high R and a statistically significant F-value when the t-values are statistically insignificant.

Mitigating Collinearity High collinearity is not a violation of any least squares assumption, but rather a lack of adequate information in the sample: 1. Collect more data with better information. 2. Impose economic restrictions as appropriate. 3. Impose statistical restrictions when justified. 4. Delete the variable which is highly collinear with other explanatory variables.

Prediction yt = 1 + 2 Xt 2 + 3 Xt 3 + εt Given a set of values for the explanatory variables, (1 X 02 X 03), the best linear unbiased predictor of y is given by: ^ y 0 = b 1 + b 2 X 02 + b 3 X 03 This predictor is unbiased in the sense that the average value of the forecast error is zero.