The Most Elegant Bump Number Algorithm Gara Pruesse

The Most Elegant Bump Number Algorithm Gara Pruesse Vancouver Island University Derek Corneil Lalla Mouatadid University of Toronto

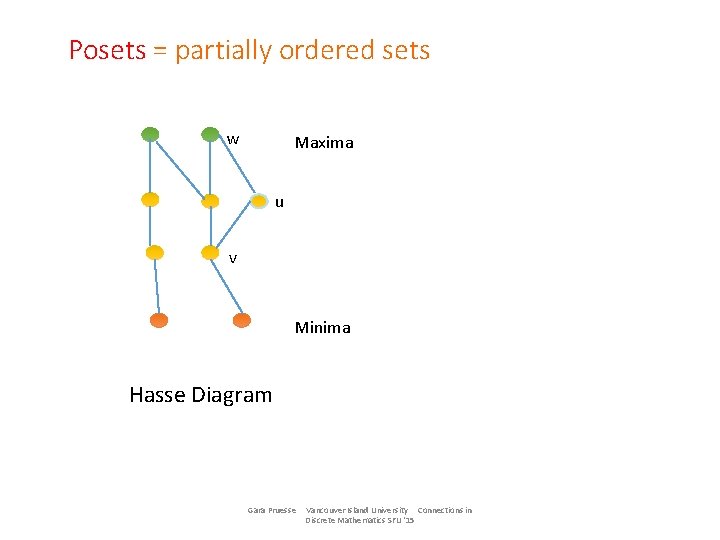
Posets = partially ordered sets w Maxima u v Minima Hasse Diagram Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

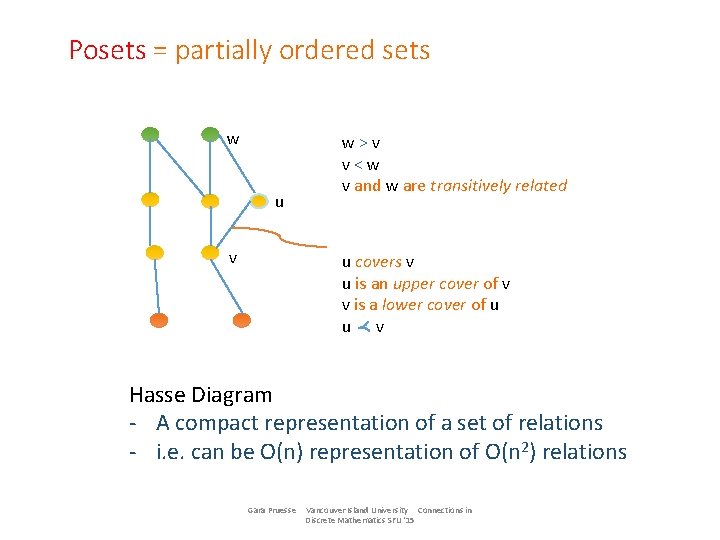
Posets = partially ordered sets w u v w>v v<w v and w are transitively related u covers v u is an upper cover of v v is a lower cover of u u v Hasse Diagram - A compact representation of a set of relations - i. e. can be O(n) representation of O(n 2) relations Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

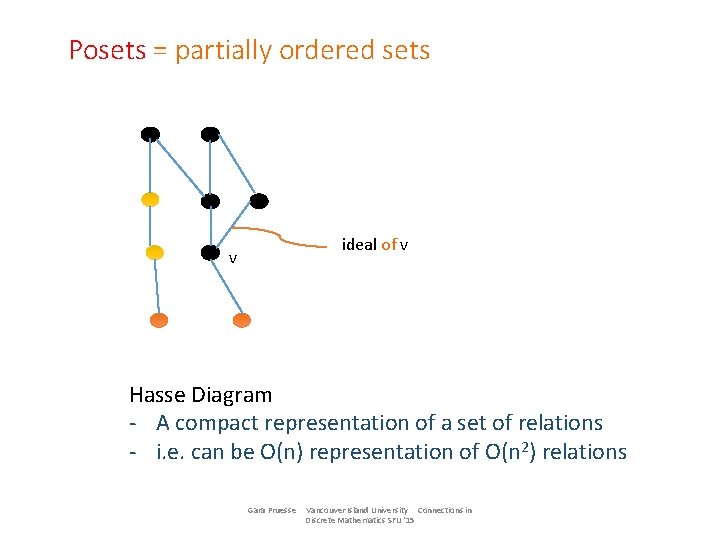
Posets = partially ordered sets ideal of v v Hasse Diagram - A compact representation of a set of relations - i. e. can be O(n) representation of O(n 2) relations Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

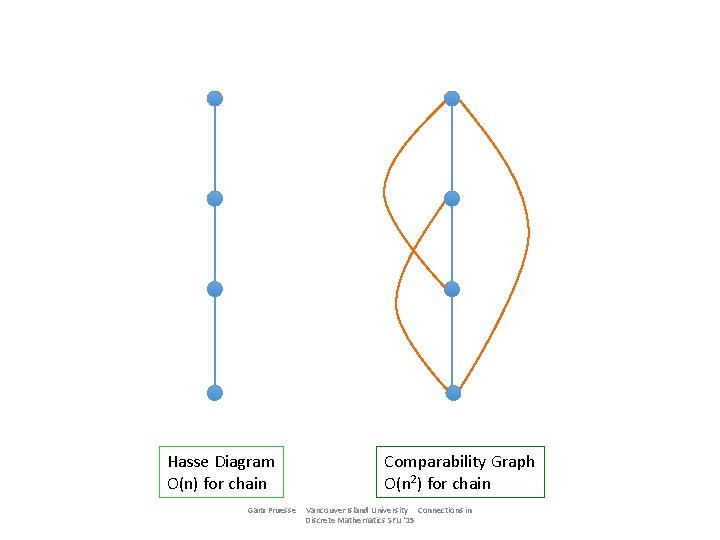
Hasse Diagram O(n) for chain Gara Pruesse Comparability Graph O(n 2) for chain Vancouver Island University Connections in Discrete Mathematics SFU '15

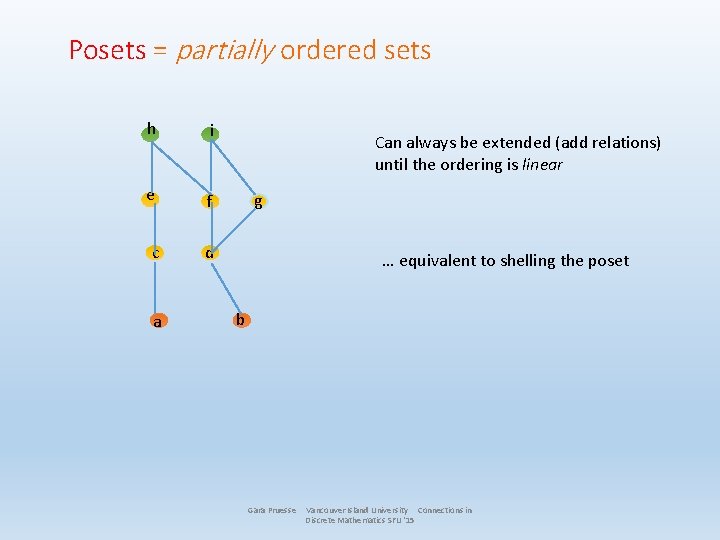
Posets = partially ordered sets h i e f c d a Can always be extended (add relations) until the ordering is linear g … equivalent to shelling the poset b Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

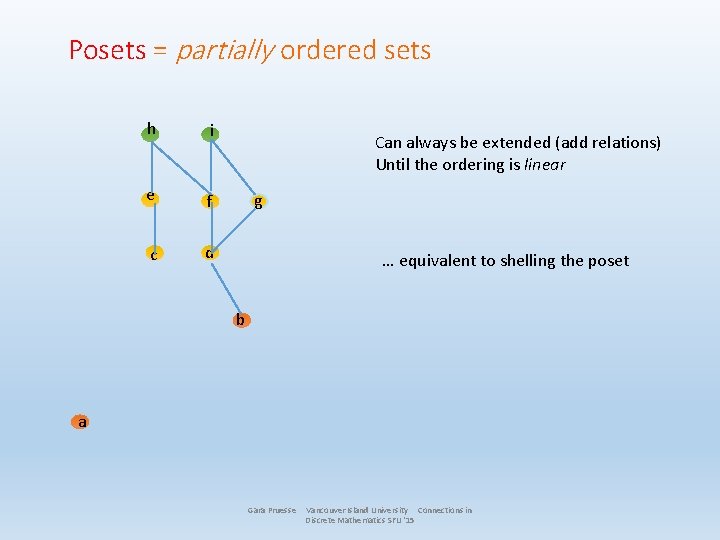
Posets = partially ordered sets h i e f c d Can always be extended (add relations) Until the ordering is linear g … equivalent to shelling the poset b a Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

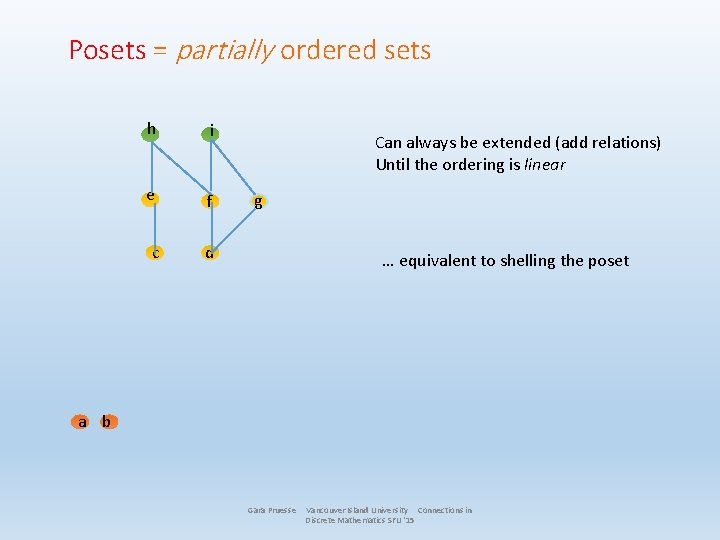
Posets = partially ordered sets h i e f c d Can always be extended (add relations) Until the ordering is linear g … equivalent to shelling the poset a b Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

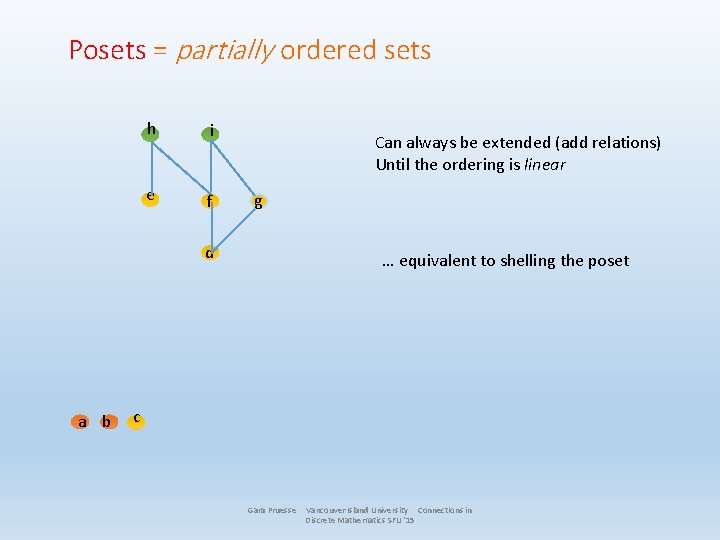
Posets = partially ordered sets h i e f Can always be extended (add relations) Until the ordering is linear g d a b … equivalent to shelling the poset c Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

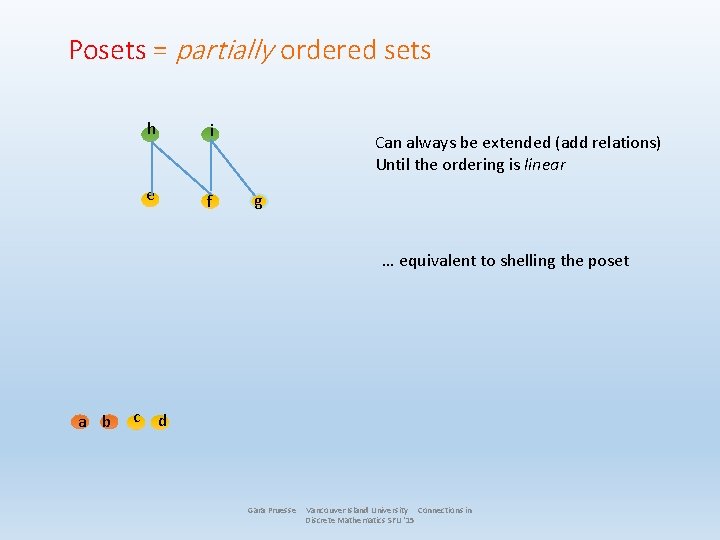
Posets = partially ordered sets h i e f Can always be extended (add relations) Until the ordering is linear g … equivalent to shelling the poset a b c d Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

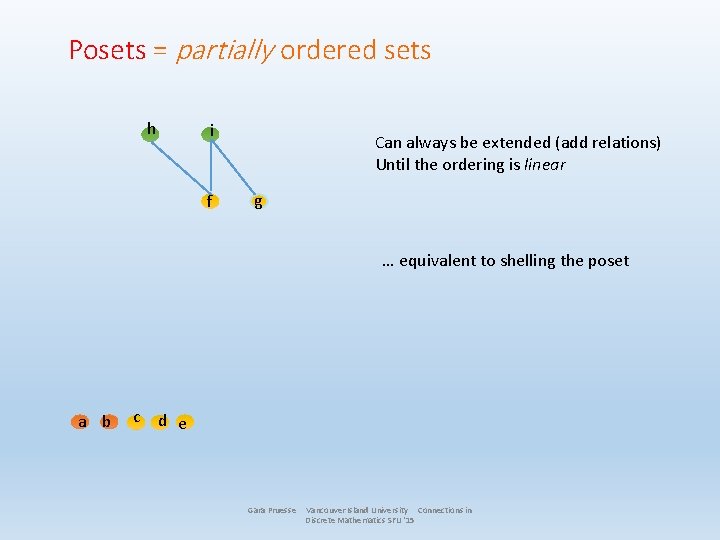
Posets = partially ordered sets h i f Can always be extended (add relations) Until the ordering is linear g … equivalent to shelling the poset a b c d e Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

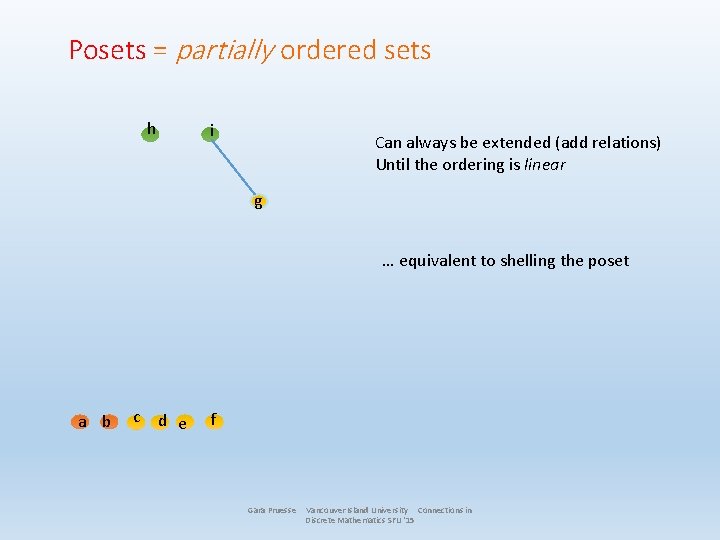
Posets = partially ordered sets h i Can always be extended (add relations) Until the ordering is linear g … equivalent to shelling the poset a b c d e f Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Posets = partially ordered sets h i Can always be extended (add relations) Until the ordering is linear … equivalent to shelling the poset a b c d e f g Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Posets = partially ordered sets i Can always be extended (add relations) Until the ordering is linear … equivalent to shelling the poset a b c d e f g h Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Posets = partially ordered sets Can always be extended (add relations) Until the ordering is linear … equivalent to shelling the poset a b c d e f g h i Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

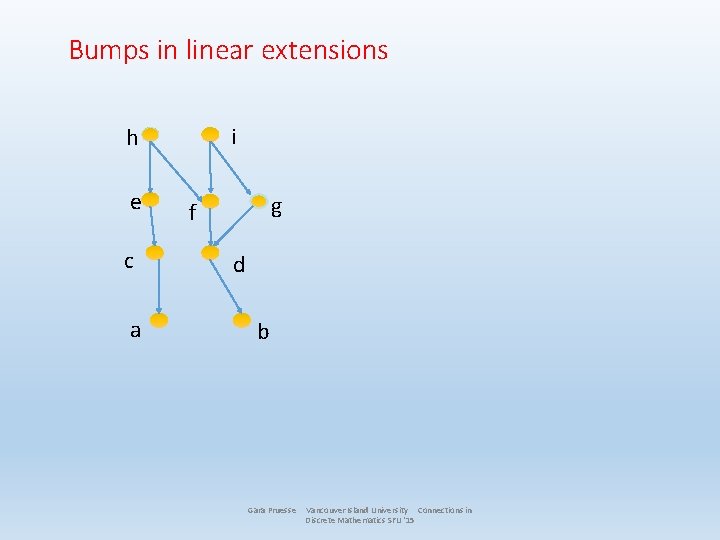
Bumps in linear extensions i h e c a g f d b Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Bumps in linear extensions i h e c a Linear extension (showing bumps) g f d b Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Bumps in linear extensions i h e c Linear extension (showing bumps) g f d b a Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Bumps in linear extensions i h e c Linear extension (showing bumps) g f d a b Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Bumps in linear extensions i h e f Linear extension (showing bumps) g c a b d Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

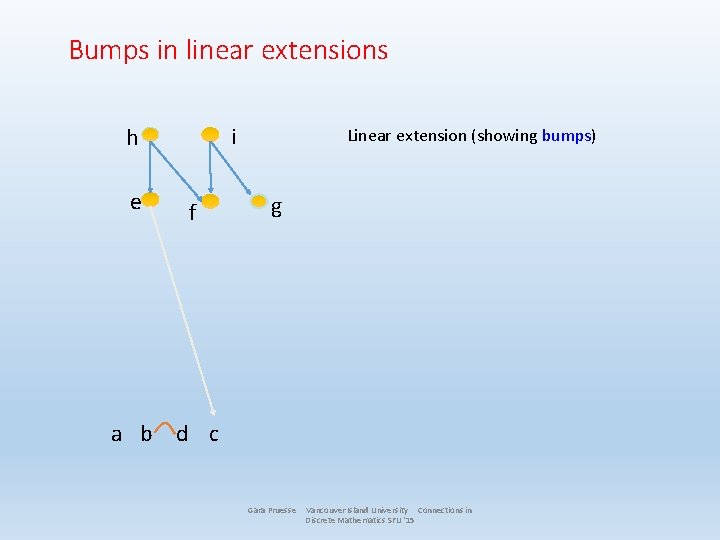
Bumps in linear extensions i h e f Linear extension (showing bumps) g a b d c Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

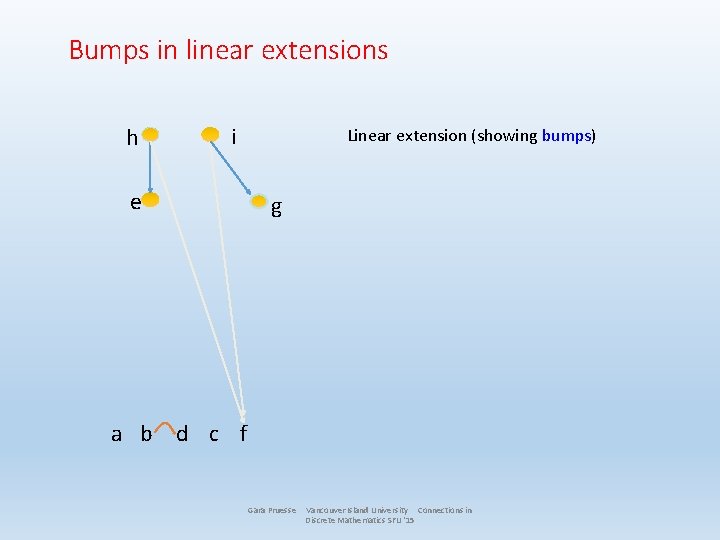
Bumps in linear extensions h i e Linear extension (showing bumps) g a b d c f Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Bumps in linear extensions h i Linear extension (showing bumps) e a b d c f g Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Bumps in linear extensions h i Linear extension (showing bumps) a b d c f g e Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Bumps in linear extensions h Linear extension (showing bumps) a b d c f g e i Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Bumps in linear extensions Linear extension (showing bumps) a b d c f g e i h Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Bump Number Problem Given poset P, what is the least number of bumps realized by a linear extension of P? b(P)= bump# of P Find an algorithm to compute b(P) and construct a linear extension with fewest bumps a b d c f g e i h Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

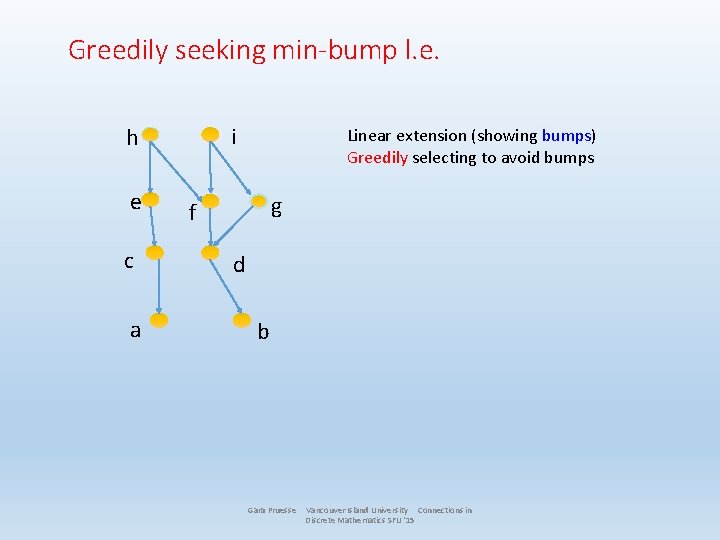
Greedily seeking min-bump l. e. i h e c a Linear extension (showing bumps) Greedily selecting to avoid bumps g f d b Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

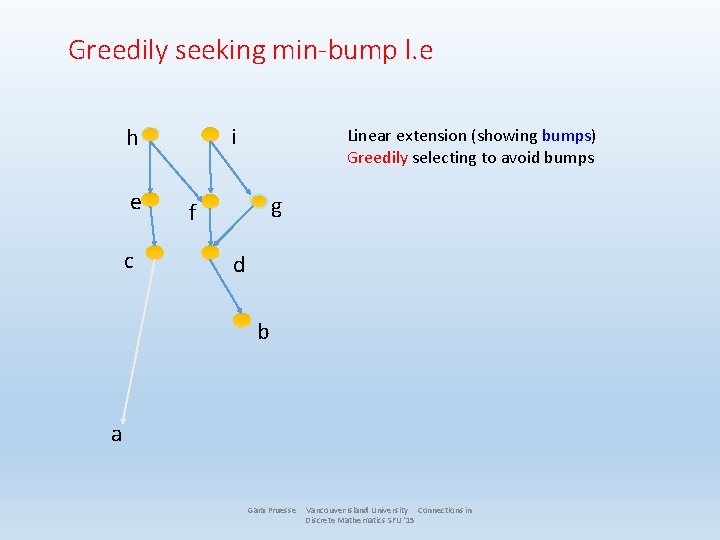
Greedily seeking min-bump l. e i h e c Linear extension (showing bumps) Greedily selecting to avoid bumps g f d b a Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedily seeking min-bump l. e i h e c Linear extension (showing bumps) Greedily selecting to avoid bumps g f d a b Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedily seeking min-bump l. e i h e Linear extension (showing bumps) Greedily selecting to avoid bumps g f d a b c Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedily seeking min-bump l. e i h e f a b c d Linear extension (showing bumps) Greedily selecting to avoid bumps g Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedily seeking min-bump l. e i h f a b Linear extension (showing bumps) Greedily selecting to avoid bumps g c d e Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

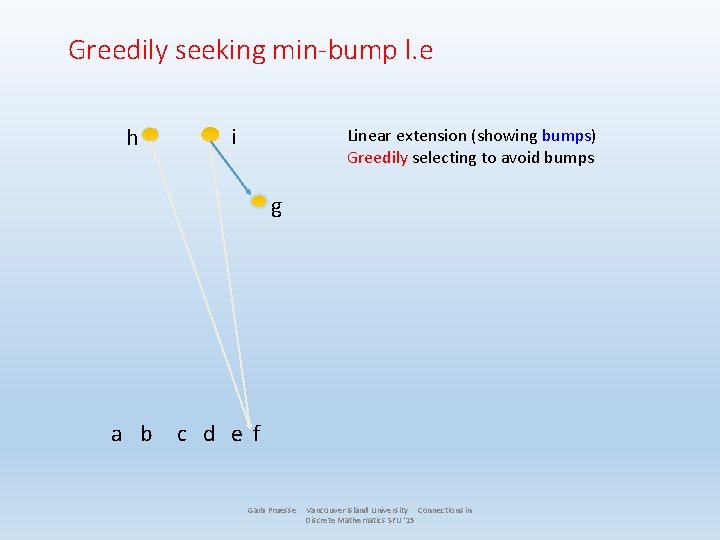
Greedily seeking min-bump l. e h i Linear extension (showing bumps) Greedily selecting to avoid bumps g a b c d e f Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedily seeking min-bump l. e h i a b c d e f g Linear extension (showing bumps) Greedily selecting to avoid bumps Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedily seeking min-bump l. e i a b Linear extension (showing bumps) Greedily selecting to avoid bumps c d e f g h Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedily seeking min-bump l. e Linear extension (showing bumps) Greedily selecting to avoid bumps a b c d e f g h i Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedily seeking min-bump l. e There is always some greedy l. e. that achieves minimum bump (Fishburn & Gehrlein, ‘ 86). For which posets does greedy always work? Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedily seeking min-bump l. e There is always some greedy l. e. that achieves minimum bump (Fishburn & Gehrlein, ‘ 86). For which posets does greedy always work? Greedy + ? works for all posets? Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedily seeking min-bump l. e There is always some greedy l. e. that achieves minimum bump (Fishburn & Gehrlein, ‘ 86). For which posets does greedy always work? F&G’ 86 Greedy + ? works for all posets? Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedily seeking min-bump l. e There is always some greedy l. e. that achieves minimum bump (Fishburn & Gehrlein, ‘ 86). For which posets does greedy always work? F&G’ 86 Greedy + ? works for all posets? This talk Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Bump Number • polynomial algorithms for interval order posets and for partial semiorder posets – both are based on the greedy shelling algorithms Fishburn and Gehrlein 1986 • polynomial algorithm for width=2 posets – not based on greedy shelling Zaguia 1987 • • polynomial algorithm for any poset – not based on shelling Habib, Möhring, Steiner 1988 • linear time algorithm – based on Gabow’s linear time 2 -proc scheduling algorithm Schäffer & Simons 1988 Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Linear Time Bump Number Schäffer & Simons 1988 relies on Gabow and Tarjan’s special case Union-Find algorithm: union and find operations known in advance O(n+m) in the cover graph … relies on hybrid linked-list / array data structure. . . Switch to array representation of tree for subtrees that are small enough… Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Algorithm, proof of correctness, and analysis • Spread across several papers • Proofs long and case-ridden • Analysis complex Question: a simple algorithm with a short proof that can be made efficient (linear time) without recourse to Special Case of Union-Find? E Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Algorithm, proof of correctness, and analysis • Spread across several papers • Proofs long and case-ridden • Analysis complex Question: a simple algorithm YES with a short proof YES that can be made efficient (linear time) without recourse to Special Case of Union-Find? Open. E Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

When Greedy is not enough d c e b ba Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15 f g

When Greedy is not enough d c eafbgcd e b ba Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15 f g

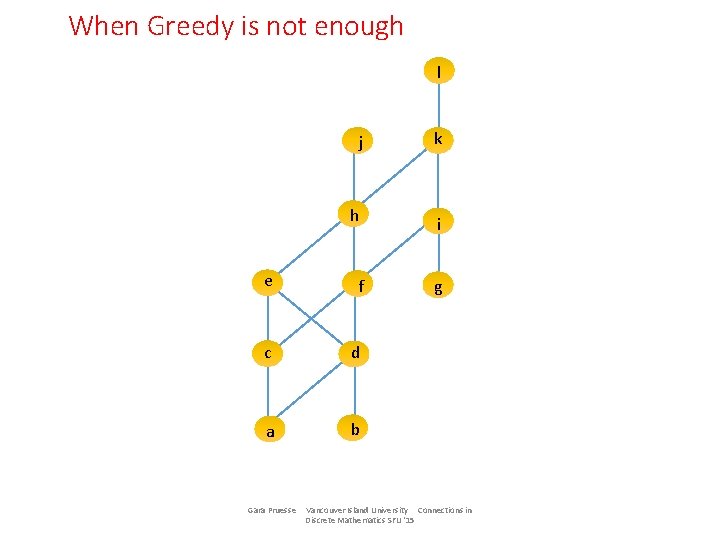
When Greedy is not enough l j k h i e f g c d a bb Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

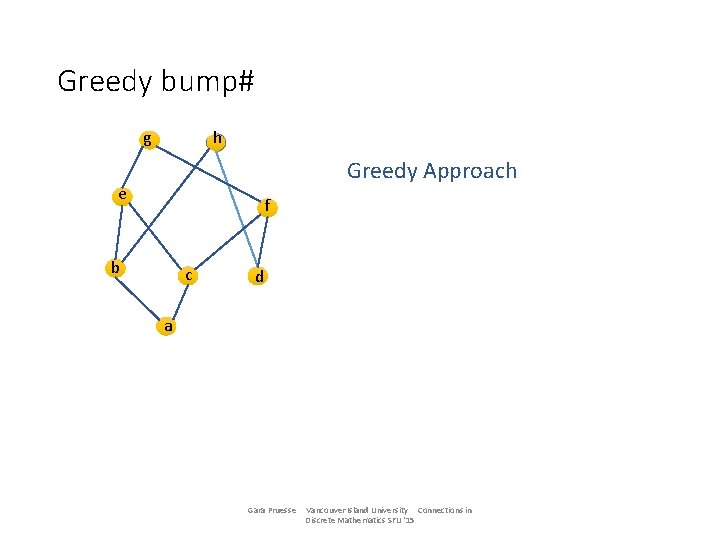
Greedy bump# g h Greedy Approach e f b c d a Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedy bump# g h Greedy Approach e f b c d a … oops d a Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

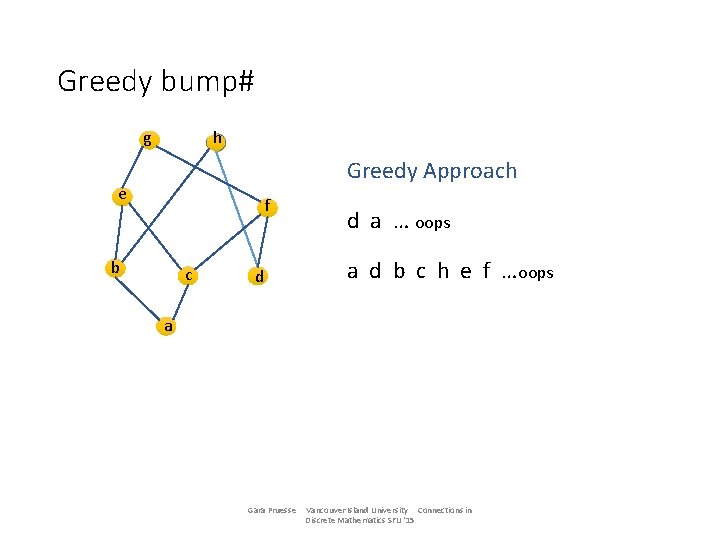
Greedy bump# g h Greedy Approach e f b c d d a … oops a d b c h e f …oops a Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

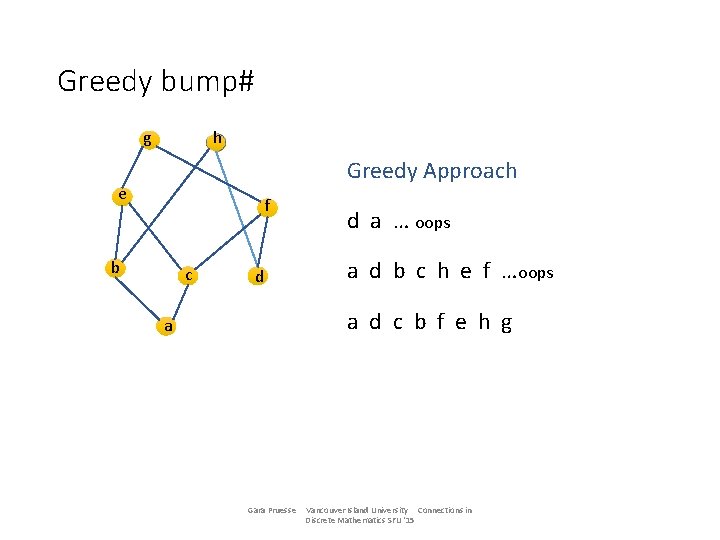
Greedy bump# g h Greedy Approach e f b c d d a … oops a d b c h e f …oops a d c b f e h g a Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

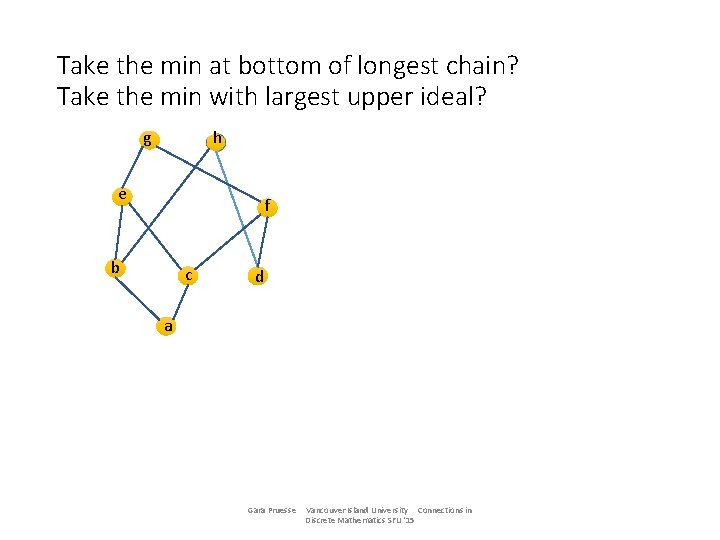
Take the min at bottom of longest chain? Take the min with largest upper ideal? g h e f b c d a Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

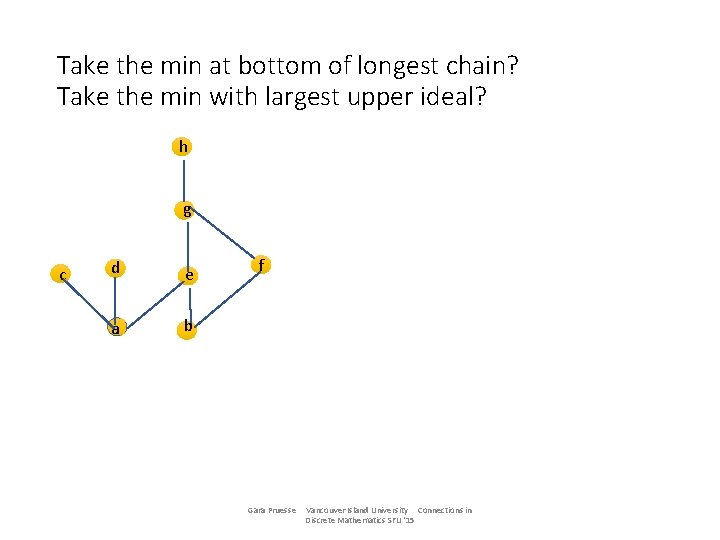
Take the min at bottom of longest chain? Take the min with largest upper ideal? h g c d e a b f Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

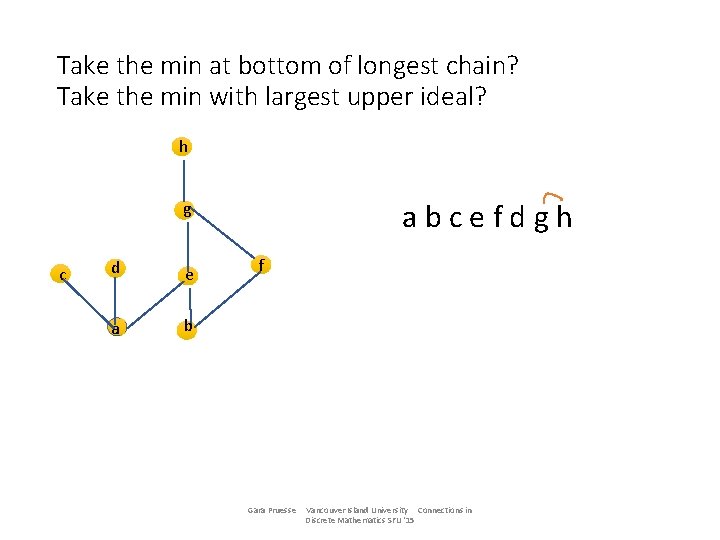
Take the min at bottom of longest chain? Take the min with largest upper ideal? h abcefdgh g c d e a b f Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

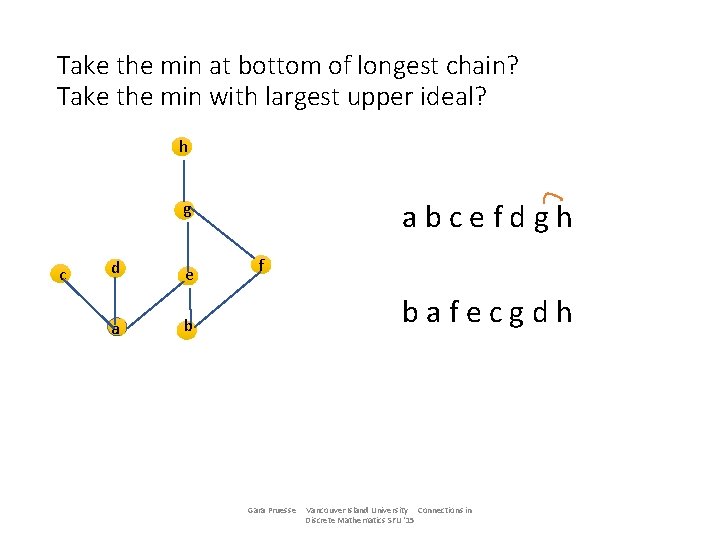
Take the min at bottom of longest chain? Take the min with largest upper ideal? h abcefdgh g c d e a b f bafecgdh Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

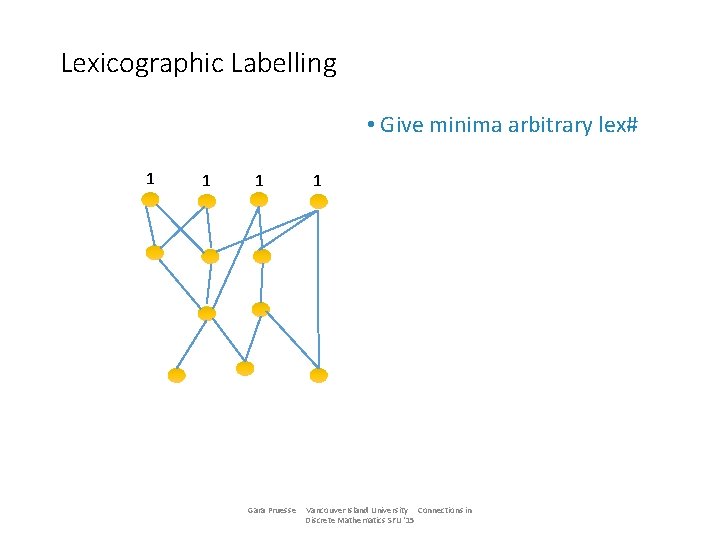
Lexicographic Labelling • Give minima arbitrary lex# 1 1 1 Gara Pruesse 1 Vancouver Island University Connections in Discrete Mathematics SFU '15

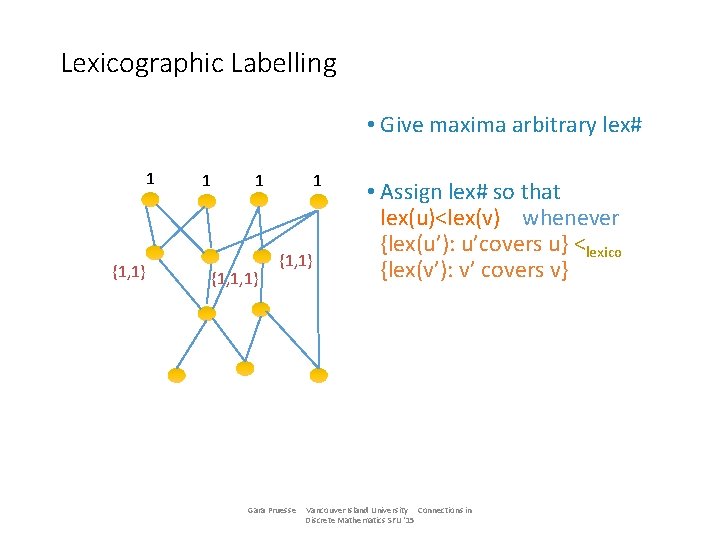
Lexicographic Labelling • Give maxima arbitrary lex# 1 {1, 1} 1 1 {1, 1, 1} 1 {1, 1} Gara Pruesse • Assign lex# so that lex(u)<lex(v) whenever {lex(u’): u’covers u} <lexico {lex(v’): v’ covers v} Vancouver Island University Connections in Discrete Mathematics SFU '15

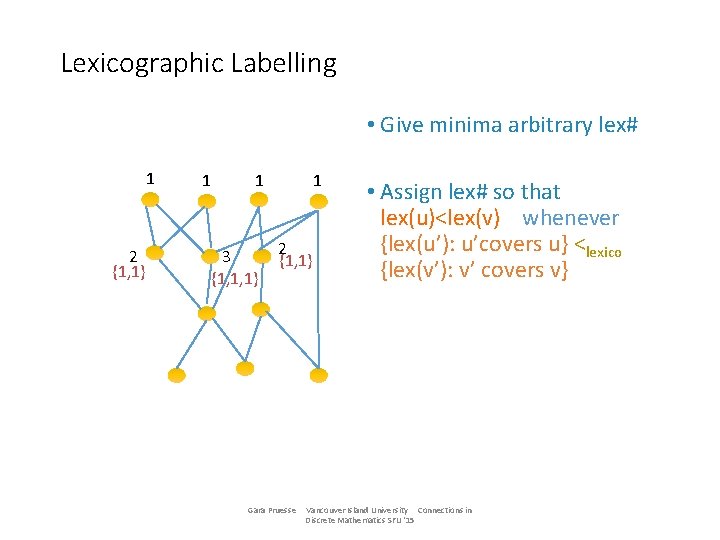
Lexicographic Labelling • Give minima arbitrary lex# 1 2 {1, 1} 1 1 3 {1, 1, 1} 1 2 {1, 1} Gara Pruesse • Assign lex# so that lex(u)<lex(v) whenever {lex(u’): u’covers u} <lexico {lex(v’): v’ covers v} Vancouver Island University Connections in Discrete Mathematics SFU '15

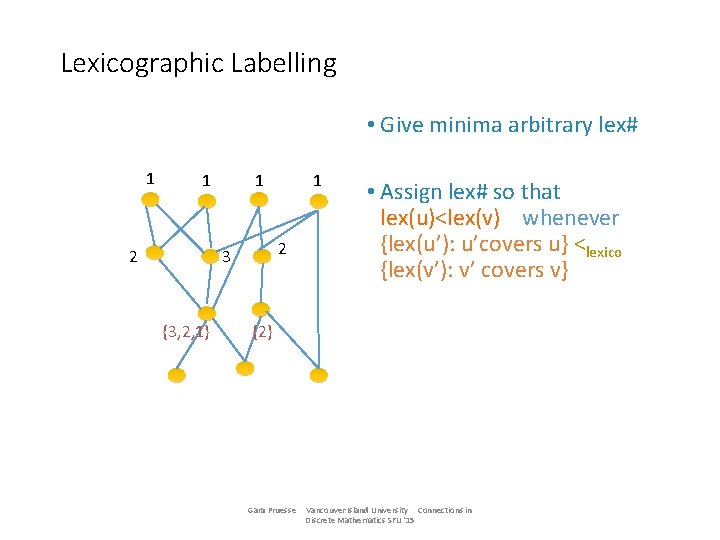
Lexicographic Labelling • Give minima arbitrary lex# 1 1 2 3 {3, 2, 1} 1 • Assign lex# so that lex(u)<lex(v) whenever {lex(u’): u’covers u} <lexico {lex(v’): v’ covers v} {2} Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

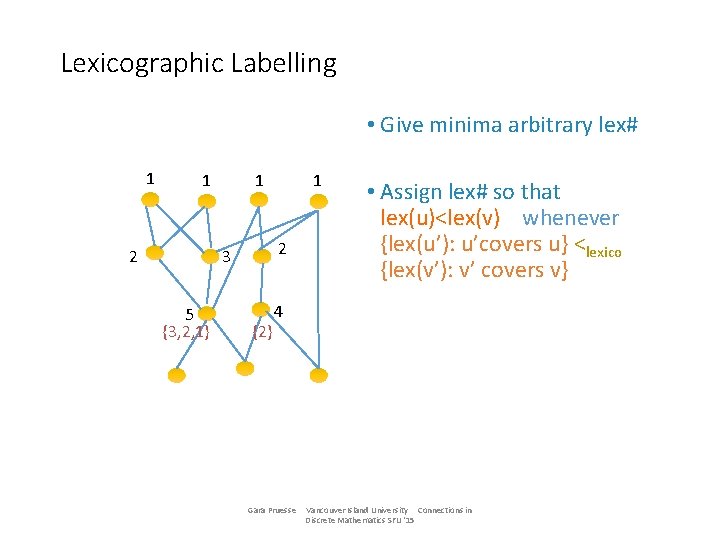
Lexicographic Labelling • Give minima arbitrary lex# 1 1 2 3 5 {3, 2, 1} 1 {2} • Assign lex# so that lex(u)<lex(v) whenever {lex(u’): u’covers u} <lexico {lex(v’): v’ covers v} 4 Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

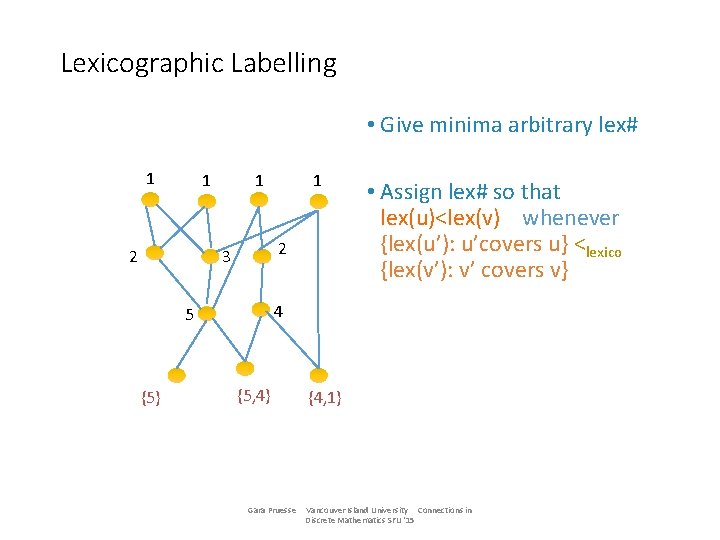
Lexicographic Labelling • Give minima arbitrary lex# 1 1 2 3 • Assign lex# so that lex(u)<lex(v) whenever {lex(u’): u’covers u} <lexico {lex(v’): v’ covers v} 4 5 {5} 1 {5, 4} Gara Pruesse {4, 1} Vancouver Island University Connections in Discrete Mathematics SFU '15

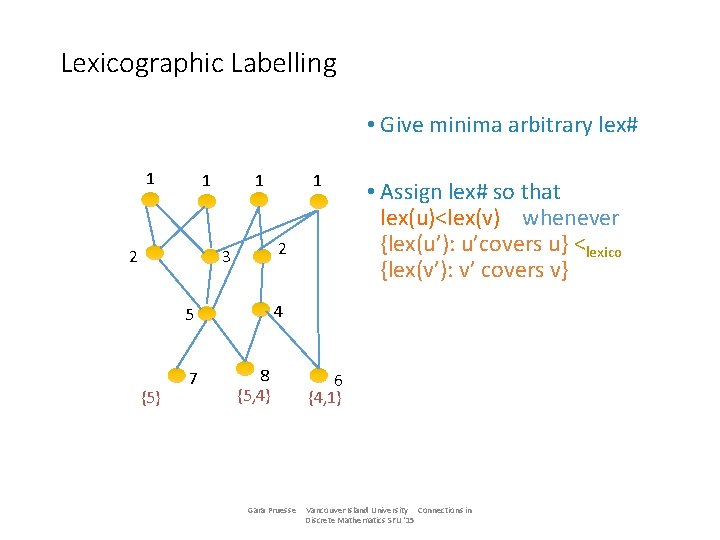
Lexicographic Labelling • Give minima arbitrary lex# 1 1 2 3 {5} • Assign lex# so that lex(u)<lex(v) whenever {lex(u’): u’covers u} <lexico {lex(v’): v’ covers v} 4 5 7 1 8 {5, 4} Gara Pruesse 6 {4, 1} Vancouver Island University Connections in Discrete Mathematics SFU '15

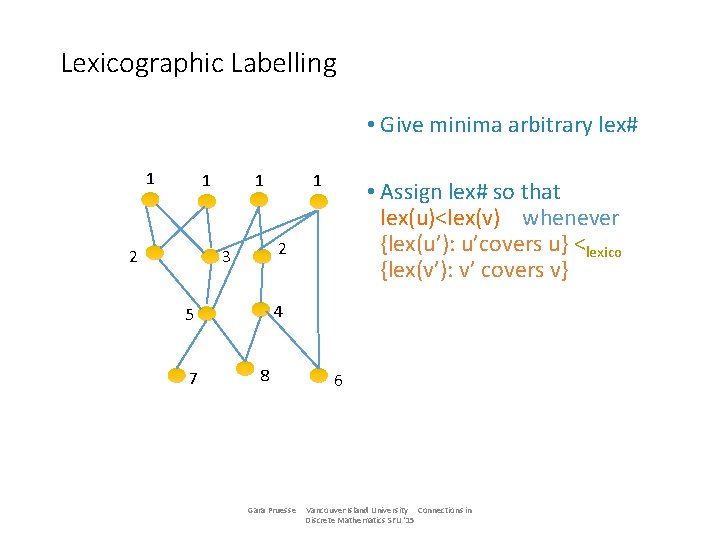
Lexicographic Labelling • Give minima arbitrary lex# 1 1 2 1 • Assign lex# so that lex(u)<lex(v) whenever {lex(u’): u’covers u} <lexico {lex(v’): v’ covers v} 2 3 4 5 7 1 8 Gara Pruesse 6 Vancouver Island University Connections in Discrete Mathematics SFU '15

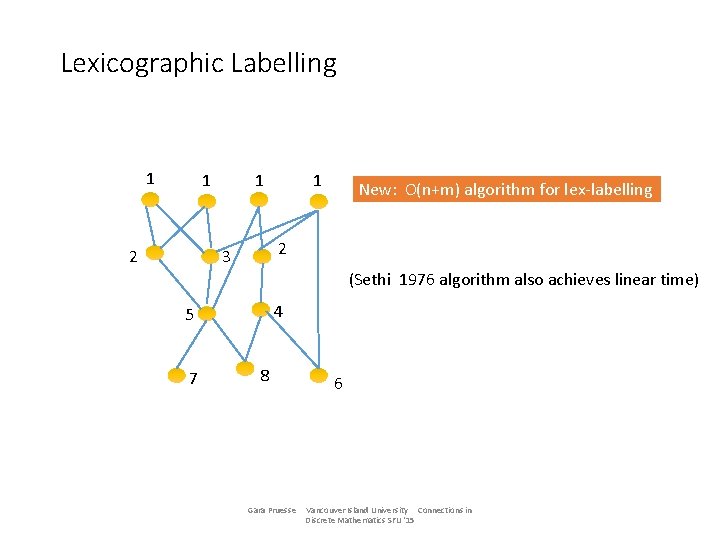
Lexicographic Labelling 1 1 2 1 1 New: O(n+m) algorithm for lex-labelling 2 3 (Sethi 1976 algorithm also achieves linear time) 4 5 7 8 Gara Pruesse 6 Vancouver Island University Connections in Discrete Mathematics SFU '15

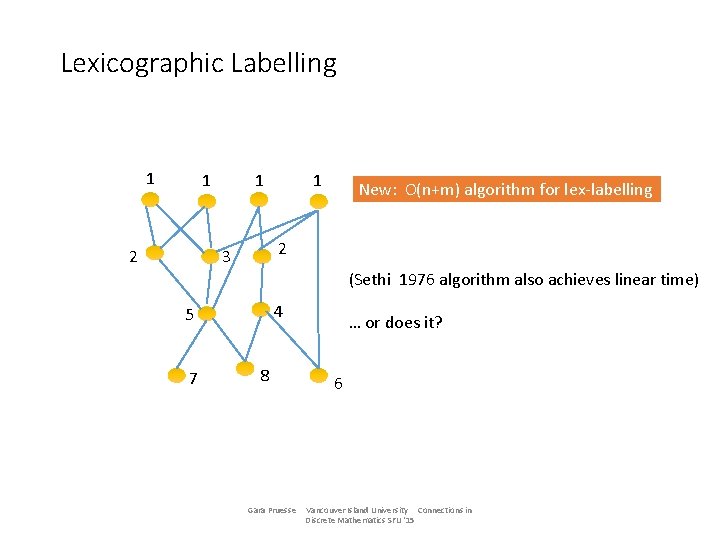
Lexicographic Labelling 1 1 2 1 1 New: O(n+m) algorithm for lex-labelling 2 3 (Sethi 1976 algorithm also achieves linear time) 4 5 7 8 Gara Pruesse … or does it? 6 Vancouver Island University Connections in Discrete Mathematics SFU '15

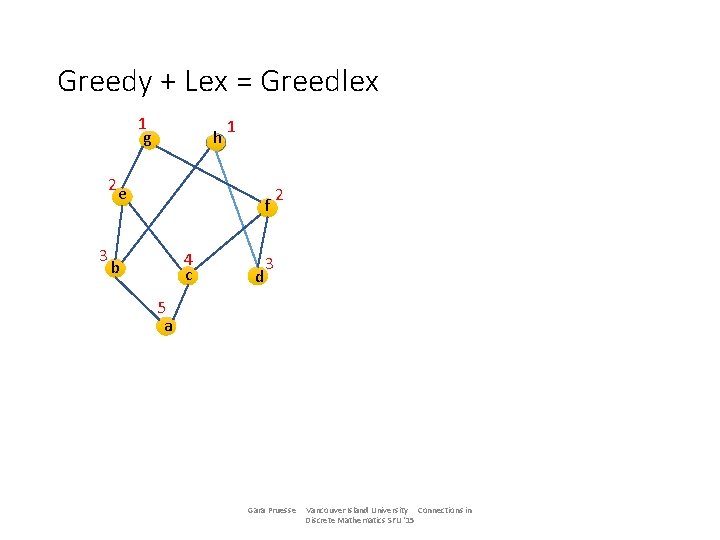
Greedy + Lex = Greedlex 1 g h 2 e 3 1 f 4 c b d 2 3 5 a Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

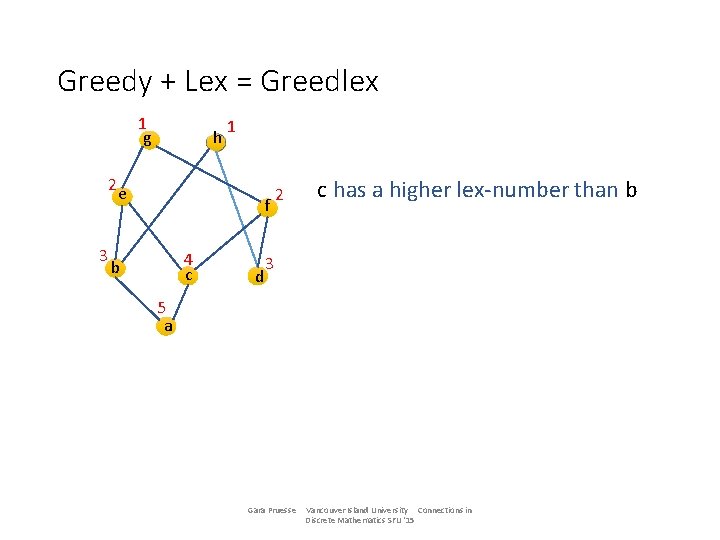
Greedy + Lex = Greedlex 1 g h 2 e 3 1 f 4 c b d 2 c has a higher lex-number than b 3 5 a Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

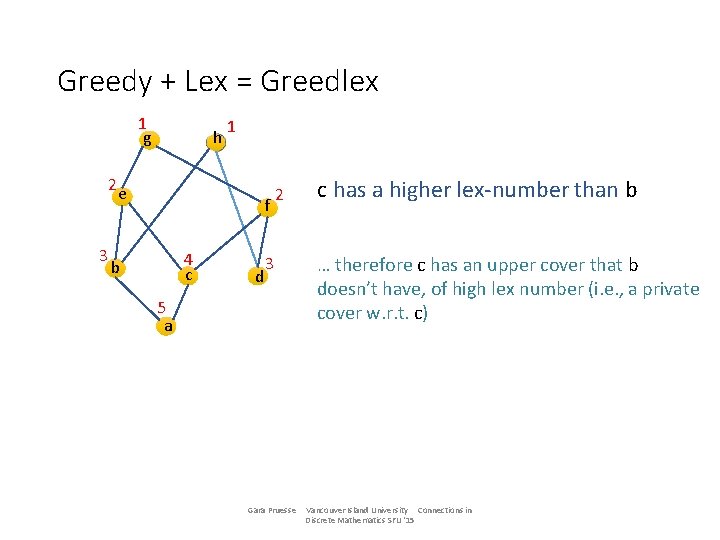
Greedy + Lex = Greedlex 1 g h 2 e 3 1 f 4 c b d 2 3 5 a Gara Pruesse c has a higher lex-number than b … therefore c has an upper cover that b doesn’t have, of high lex number (i. e. , a private cover w. r. t. c) Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedy + Lex = Greedlex 1 g h e 3 1 f 4 c b d 2 3 5 a Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

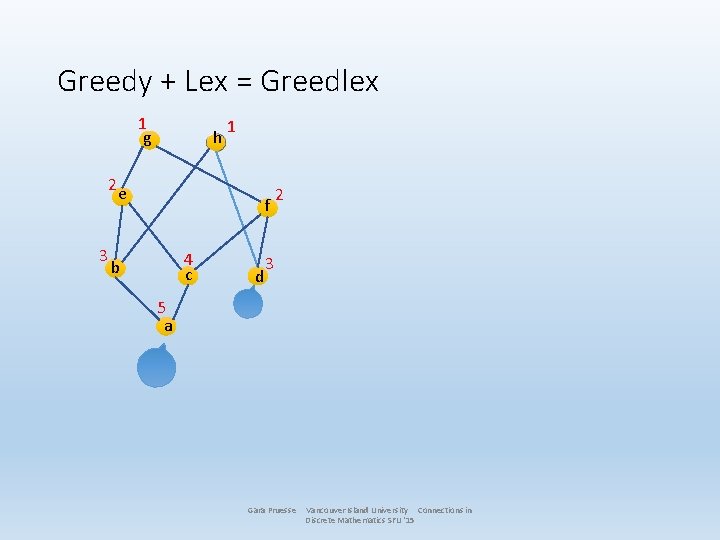
Greedy + Lex = Greedlex 1 g h 2 e 3 1 f 4 c b d 2 3 5 a Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

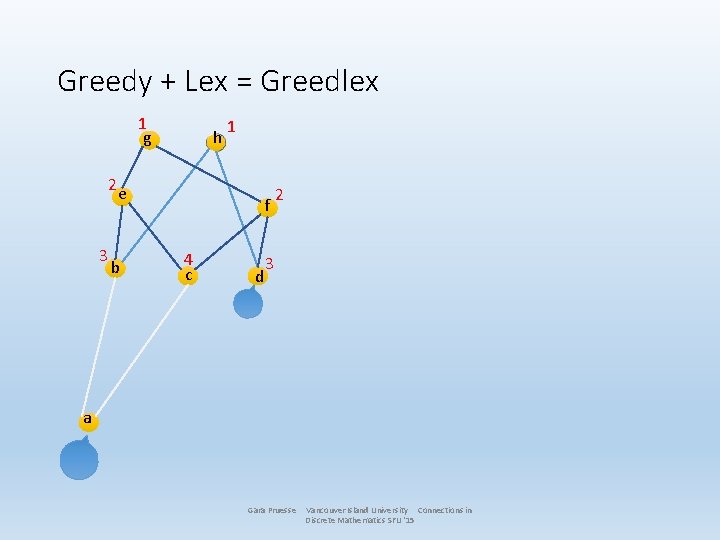
Greedy + Lex = Greedlex 1 g h 2 e 3 b 1 f 4 c d 2 3 a Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

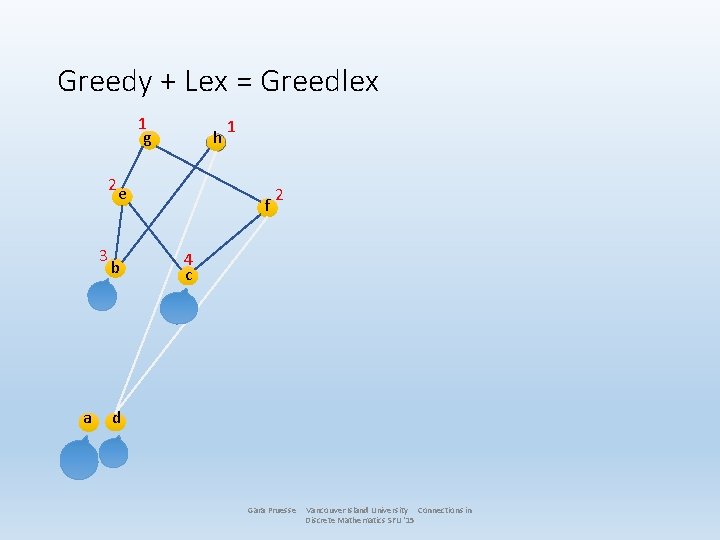
Greedy + Lex = Greedlex 1 g h 2 e 3 a b 1 f 2 4 c d Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

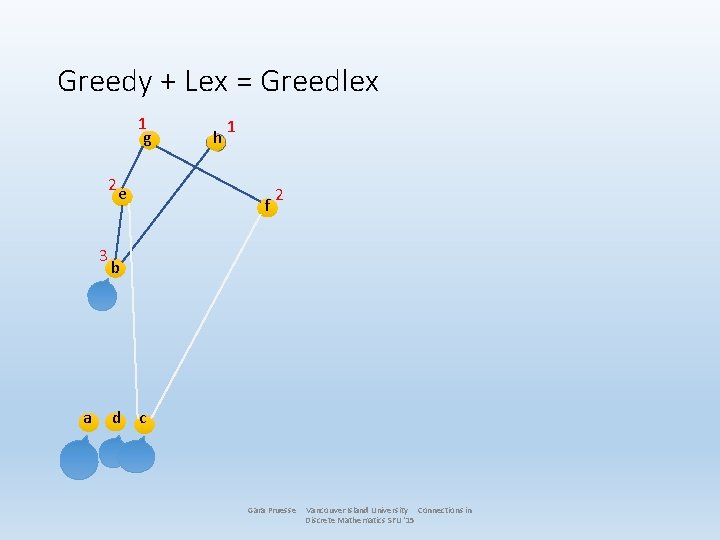
Greedy + Lex = Greedlex 1 g 2 e 3 a h 1 f 2 b d c Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

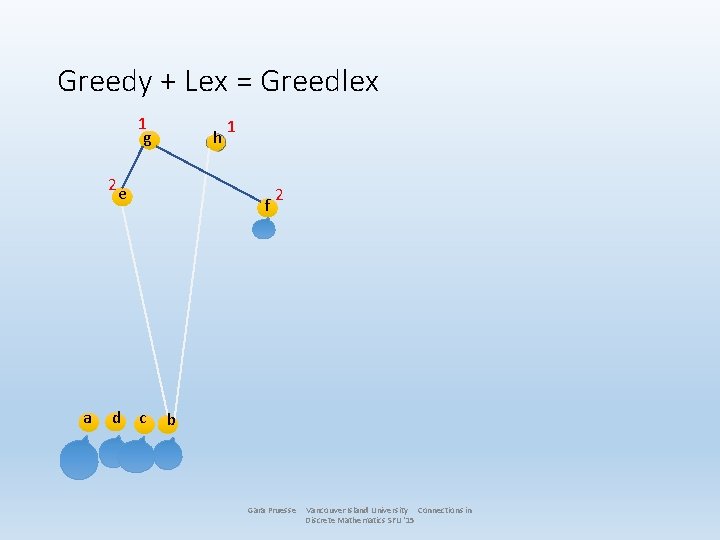
Greedy + Lex = Greedlex 1 g h 2 e a d c 1 f 2 b Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedy + Lex = Greedlex 1 g h 1 2 e a d c b f Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedy + Lex = Greedlex a 1 g h d c b f e 1 Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedy + Lex = Greedlex 1 g a d c b f e h Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedy + Lex = Greedlex a d c b f e h g Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedy + Lex = Greedlex • Label the elements lexicographically • Shell greedily (avoiding bumps locally) and take the lexicographically largest when given a choice a d c b f e h g Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Greedy + Lex = Greedlex • Label the elements lexicographically • Shell greedily (avoiding bumps locally) and take the lexicographically largest when given a choice Claim: This always yields the min-bump l. e. Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Lex-Yanking Lemma b xxx. . x a xx…x has k bumps and a is min Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Lex-Yanking Lemma b xxx. . x a xx…x has k bumps and a is min l. e. a x’x’x’…b…x’ with k or fewer bumps (Balloon size indicates relative Lex value) Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15 E

Lex-Yanking Lemma b xxx. . x a xx…x has k bumps and a is min l. e. a x’x’x’…b…x’ with k or fewer bumps E (Balloon size indicates relative Lex value) Claim: If the lex-yanking lemma holds on a poset and all its induced subposets, then Greedlex produces a bump-optimal linear extension. Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

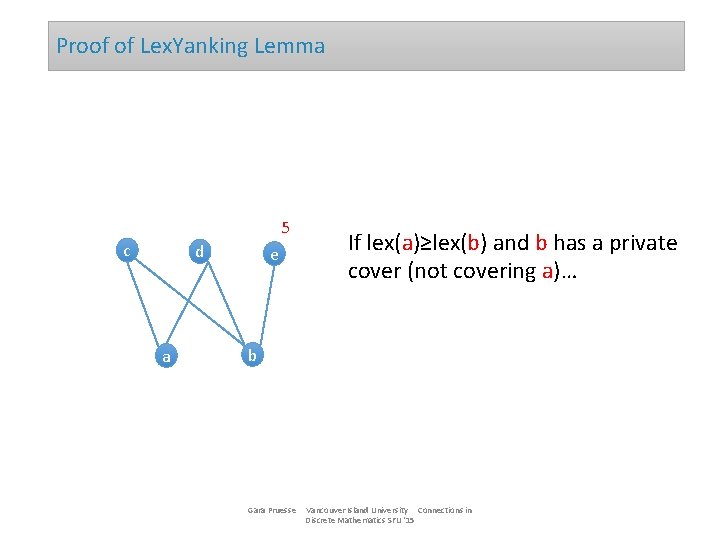
Proof of Lex. Yanking Lemma 5 c d a e If lex(a)≥lex(b) and b has a private cover (not covering a)… b Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

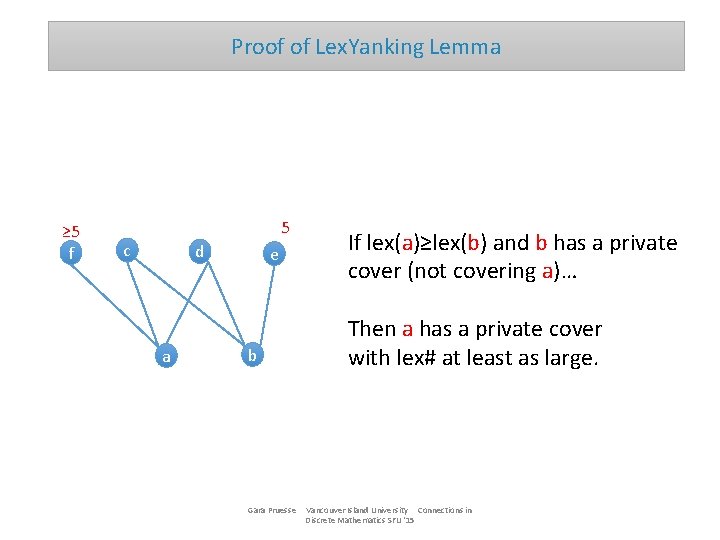
Proof of Lex. Yanking Lemma ≥ 5 f 5 c d a e b Gara Pruesse If lex(a)≥lex(b) and b has a private cover (not covering a)… Then a has a private cover with lex# at least as large. Vancouver Island University Connections in Discrete Mathematics SFU '15

Proof of Lex. Yanking Lemma By induction on n=|V(P)|. Base cases n=0, 1 are trivial. Let P be a poset on n>1 elements, and suppose Lex. Yanking Lemma holds for all smaller posets. (Then also Greedlex works on smaller posets. ) b xxx a xxxx a l. e. with k bumps, lex(a)≥lex(b), a and b min aa b Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Proof of Lex. Yanking Lemma b xxx a xxxx a l. e. with k bumps, lex(a)≥lex(b), a and b min The poset {b} is smaller, so by Ind. Hyp. , Lex. Yanking holds, and Greedlex produces a min-bump suffix to follow b b yyy a yyyy All these elements have lex# > lex(a) aa b Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Proof of Lex. Yanking Lemma b xxx a xxxx a l. e. with k bumps, lex(a)≥lex(b), a and b min The poset {b} is smaller, so by Ind. Hyp. , Lex. Yanking holds, and Greedlex produces a min-bump suffix to follow b yyy a yyyy All these elements have lex# > lex(a) ≥ lex(b) aa b Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Proof of Lex. Yanking Lemma b xxx a xxxx a l. e. with k bumps, lex(a)≥lex(b), a and b min The poset {b} is smaller, so by Ind. Hyp. , Lex. Yanking holds, and Greedlex produces a min-bump suffix to follow b yyy a yyyy All these elements have lex# > lex(a) ≥ lex(b) Hence all are incomparable with b They are also incomparable with a aa b Swap: a yyy b yyyy Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Proof of Lex. Yanking Lemma b xxx a xxxx a l. e. with k bumps, lex(a)≥lex(b), a and b min The poset {b} is smaller, so by Ind. Hyp. , Lex. Yanking holds, and Greedlex produces a min-bump suffix to follow b yyy a yyyy All these elements have lex# > lex(a) ≥ lex(b) Hence all are incomparable with b They are also incomparable with a aa b Swap: a yyy b yyyy May have introduced a bump Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Proof of Lex. Yanking Lemma a yyy b yyyy Suppose a bump was introduced after the b, and there was no such bump when a was in the same spot. Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Proof of Lex. Yanking Lemma a yyy b y 1 yyy Suppose a bump was introduced after the b, and there was no such bump when a was in the analogous spot. Then y 1 is a private cover of b (with respect to a). Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Proof of Lex. Yanking Lemma a yyy b y 1 yyy Suppose a bump was introduced after the b, and there was no such bump when a was in the same spot. Then y 1 is a private cover of b (with respect to a). Then a has some private cover c (w. r. t. b), with lex(c)≥ lex(y 1). a yyy b y 1 y…c. . y Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Proof of Lex. Yanking Lemma a yyy b y 1 yyy Suppose a bump was introduced after the b, and there was no such bump when a was in the same spot. Then y 1 is a private neighbour of b (with respect to a). Then a has some private neighbour c (w. r. t. b), with lex(c)≥ lex(y 1). Then c can be yanked forward in the suffix, a yyy b y 1 y…c. . y by the Ind. Hyp. , without increasing bumps a yyy b c z…y 1. . z Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Proof of Lex. Yanking Lemma a yyy b y 1 yyy Suppose a bump was introduced after the b, and there was no such bump when a was in the same spot. Then y 1 is a private neighbour of b (with respect to a). Then a has some private neighbour c (w. r. t. b), with lex(c)≥ lex(y 1). Then c can be yanked forward in the suffix, a yyy b y 1 y…c. . y by the Ind. Hyp. , without increasing bumps a yyy b c z…y 1. . z and destroying the bump after b. [if c is not a min, take c’s descendent]. Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

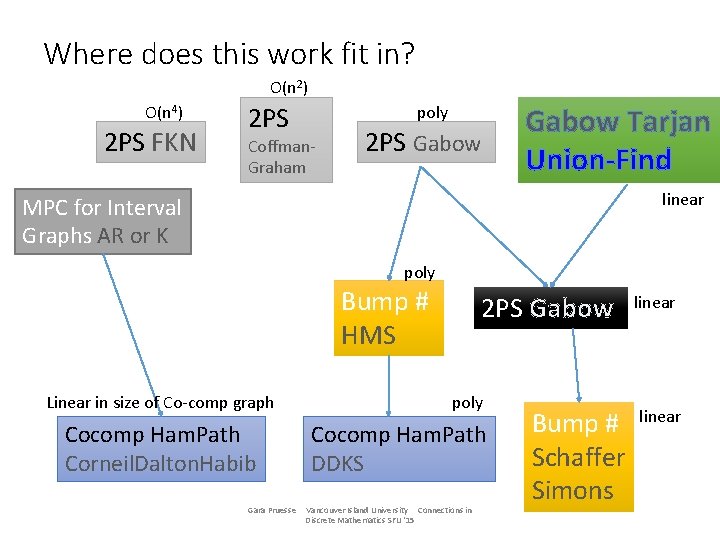
Where does this work fit in? O(n 2) O(n 4) 2 PS FKN 2 PS poly Coffman. Graham 2 PS Gabow Tarjan Union-Find linear MPC for Interval Graphs AR or K poly Bump # HMS Linear in size of Co-comp graph Cocomp Ham. Path Corneil. Dalton. Habib Gara Pruesse 2 PS Gabow poly Cocomp Ham. Path DDKS Vancouver Island University Connections in Discrete Mathematics SFU '15 Bump # Schaffer Simons linear

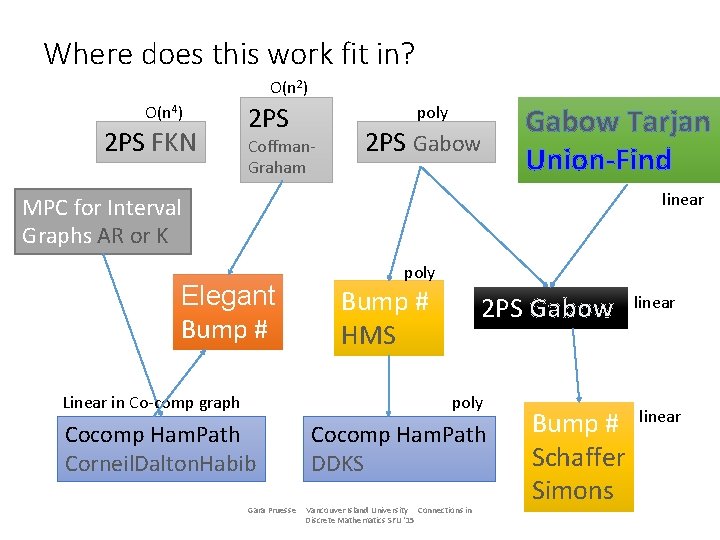
Where does this work fit in? O(n 2) O(n 4) 2 PS FKN 2 PS poly Coffman. Graham 2 PS Gabow Tarjan Union-Find linear MPC for Interval Graphs AR or K Elegant Bump # poly Bump # HMS 2 PS Gabow poly Linear in Co-comp graph Cocomp Ham. Path Corneil. Dalton. Habib Gara Pruesse Cocomp Ham. Path DDKS Vancouver Island University Connections in Discrete Mathematics SFU '15 Bump # Schaffer Simons linear

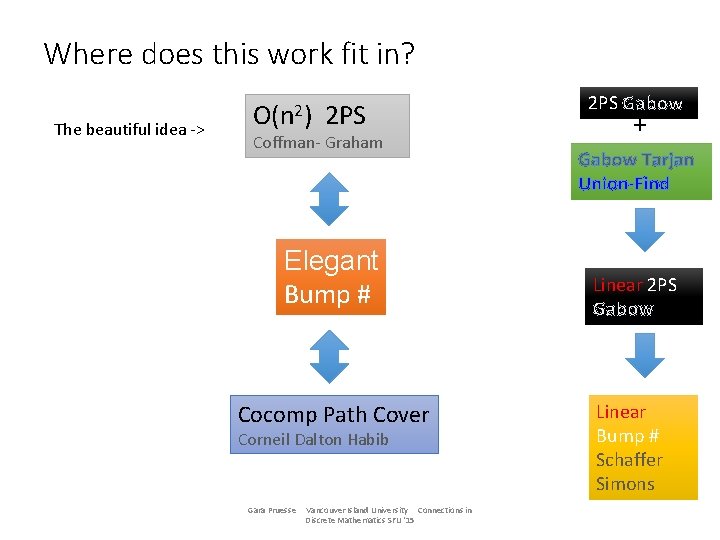
Where does this work fit in? The beautiful idea -> O(n 2) 2 PS Coffman- Graham Elegant Bump # Cocomp Path Cover Corneil Dalton Habib Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15 2 PS Gabow + Gabow Tarjan Union-Find Linear 2 PS Gabow Linear Bump # Schaffer Simons

How fast is the Elegant Algorithm? • O(n log w) w is size of maximum antichain n is size of the cover graph • Can be quickly programmed Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

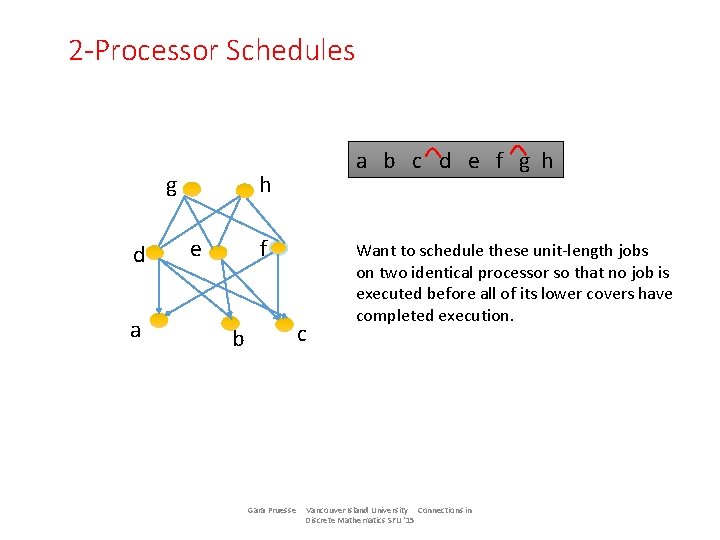
2 -Processor Schedules g d a a b c d e f g h h e f c b Gara Pruesse Want to schedule these unit-length jobs on two identical processor so that no job is executed before all of its lower covers have completed execution. Vancouver Island University Connections in Discrete Mathematics SFU '15

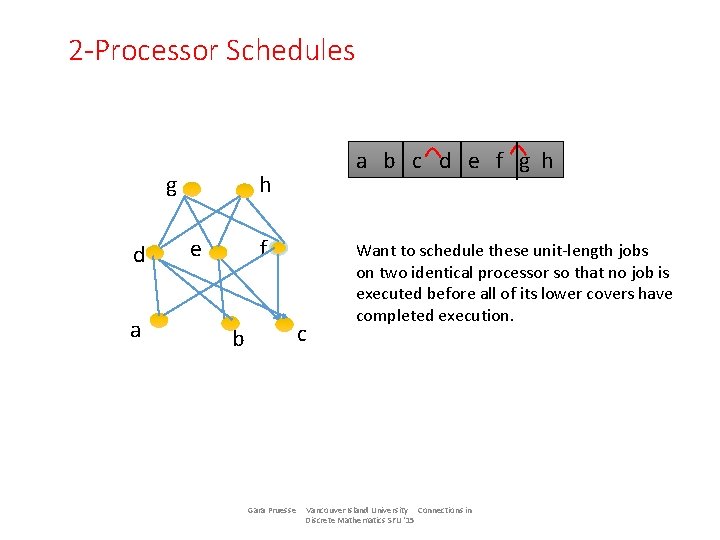
2 -Processor Schedules g d a a b c d e f g h h e f c b Gara Pruesse Want to schedule these unit-length jobs on two identical processor so that no job is executed before all of its lower covers have completed execution. Vancouver Island University Connections in Discrete Mathematics SFU '15

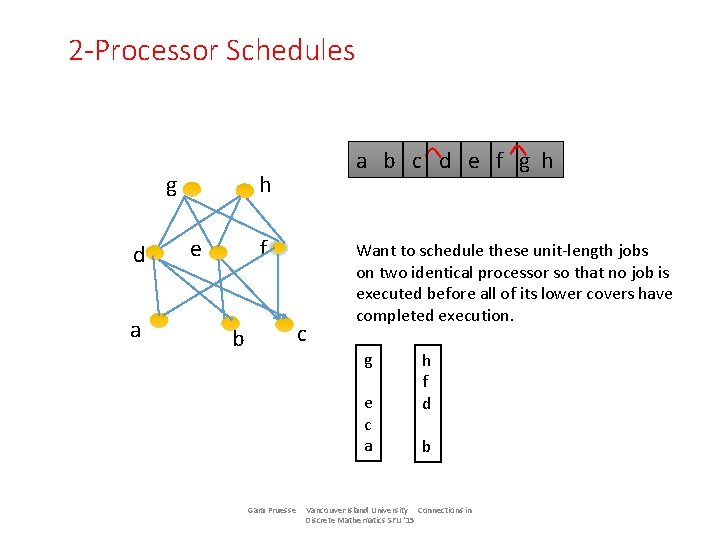
2 -Processor Schedules g d a a b c d e f g h h e f c b Want to schedule these unit-length jobs on two identical processor so that no job is executed before all of its lower covers have completed execution. g e c a Gara Pruesse h f d b Vancouver Island University Connections in Discrete Mathematics SFU '15

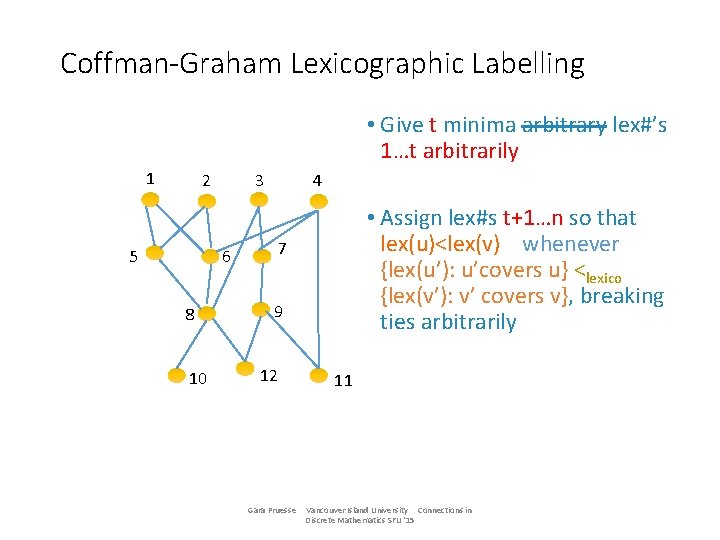
Coffman-Graham Lexicographic Labelling • Give t minima arbitrary lex#’s 1…t arbitrarily 1 2 5 3 6 8 10 4 • Assign lex#s t+1…n so that lex(u)<lex(v) whenever {lex(u’): u’covers u} <lexico {lex(v’): v’ covers v}, breaking ties arbitrarily 7 9 12 Gara Pruesse 11 Vancouver Island University Connections in Discrete Mathematics SFU '15

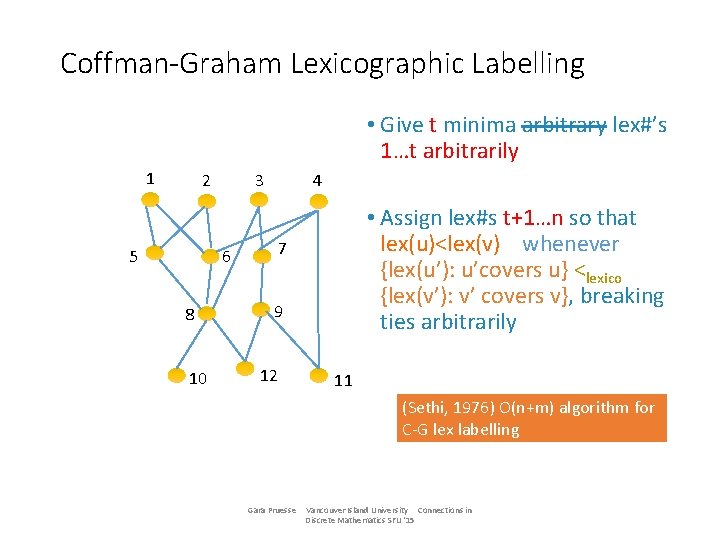
Coffman-Graham Lexicographic Labelling • Give t minima arbitrary lex#’s 1…t arbitrarily 1 2 5 3 6 8 10 4 • Assign lex#s t+1…n so that lex(u)<lex(v) whenever {lex(u’): u’covers u} <lexico {lex(v’): v’ covers v}, breaking ties arbitrarily 7 9 12 11 (Sethi, 1976) O(n+m) algorithm for C-G lex labelling Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Lexicographic Labelling and 2 PS • Coffman and Graham ‘ 72 used it for 2 -proc scheduling O(n 2) 1 1 2 1 • Sethi ’ 76 also used it for a 2 PS; lex labelling takes O(n + m) though the remainder of the 2 PS alg takes O(n α(n) + m)) 2 3 4 5 7 1 8 Gara Pruesse 6 Vancouver Island University Connections in Discrete Mathematics SFU '15

Further Work Completed: • Solve 2 -Proc Sched using Greedlex • Greedlex can work on either transitive closure or transitive reduction • Greedlex can generate all min-bump linear extensions (all Min. Path Covers in Cocomp graphs) Open: • Show to do it all in linear time • What if the communication delays are weighted? • What about representations that are in between transitive closure and reduction? • What about AT-free graphs? • Contains the cocomp graphs Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Thank You! Gara Pruesse Vancouver Island University Coauthors: Derek Corneil Lalla Mouatadid University of Toronto Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15

Hamiltonicity of Cocomp Graphs Keil 1985 • Ham’n cycle in Interval graphs alg Deogun Steiner 1990 • Poly-time Ham’n Cycle Deogun Kratsch Steiner 1997 • 1 -tough cocomp graphs are hamiltonian – Damaschke Deogun Kratsch Steiner 1991 • Hamilton Path in cocomps using bump number algorithm Corneil Dalton Habib 2013 • Min Path Cover Alg (certified) in Cocomp Graphs Gara Pruesse Vancouver Island University Connections in Discrete Mathematics SFU '15