The Modelica MultiBond Graph Library A bondgraphic modeling

The Modelica Multi-Bond Graph Library A bondgraphic modeling tool and its application in mechanics. Dirk Zimmer François E. Cellier Institute of Computational Science Department of Computer Science ETH Zürich Conference 2006

Abstract ETH Zürich Departement of Computer Science Institute of Computational Science • Multi-bond graphs are a general, graphical modeling tool for multi-dimensional physical processes. This presentation introduces their Modelica implementation: The Multi. Bond. Lib. • Multi-bond graphs are especially well suited for modeling mechanical systems. The Multi. Bond. Lib offers a partial reimplementation of the standard Multi. Body library. © Dirk Zimmer, September 2006, Slide 2

ETH Overview Zürich Departement of Computer Science Institute of Computational Science • Introduction to bond graphs • Presentation of multi-bond graphs • 2 D- and 3 D-mechanical models • Conclusions © Dirk Zimmer, September 2006, Slide 3

Introduction to Bond Graphs 1 • ETH Zürich Departement of Computer Science Institute of Computational Science Elements of a physical system have a certain behavior with respect to power and energy. A battery is a source of energy. – A thermal capacitance stores energy. – A mechanical damper dissipates energy. – Power is being distributed along specified paths. – • These concepts suggest a general modeling approach for physical systems: bond graphs. © Dirk Zimmer, September 2006, Slide 4

Introduction to Bond Graphs 2 ETH Zürich Departement of Computer Science Institute of Computational Science • Bond graphs are a modeling tool for continuous physical systems. They form a directed graph where the vertices represent the physical elements. • The edges of the graph are the bonds themselves. e f • A bond represents a power flow. It carries two adjugate variables: the effort e and the flow f. The product of them is power. © Dirk Zimmer, September 2006, Slide 5

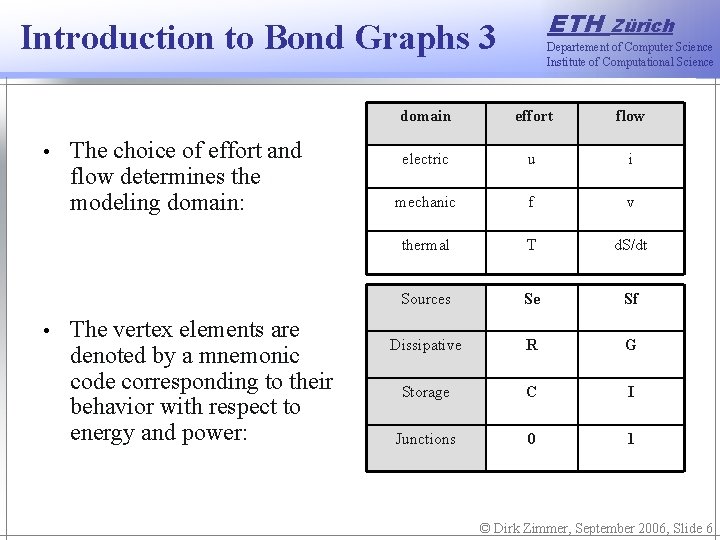
ETH Introduction to Bond Graphs 3 • • The choice of effort and flow determines the modeling domain: The vertex elements are denoted by a mnemonic code corresponding to their behavior with respect to energy and power: Zürich Departement of Computer Science Institute of Computational Science domain effort flow electric u i mechanic f v thermal T d. S/dt Sources Se Sf Dissipative R G Storage C I Junctions 0 1 © Dirk Zimmer, September 2006, Slide 6

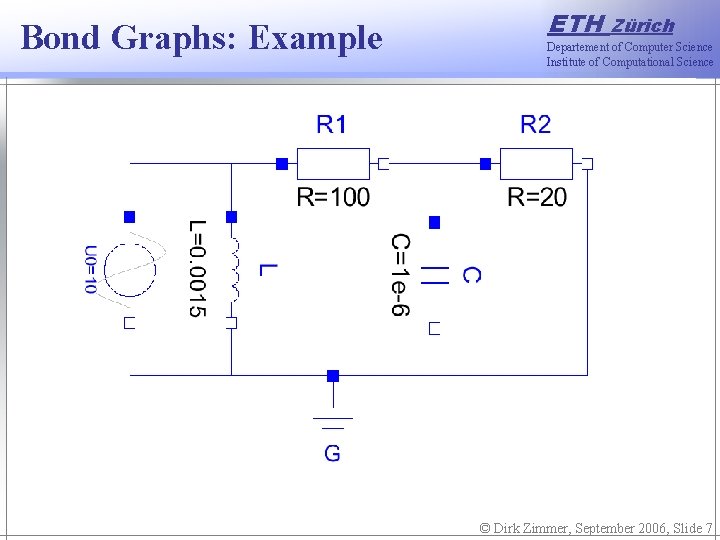
Bond Graphs: Example ETH Zürich Departement of Computer Science Institute of Computational Science © Dirk Zimmer, September 2006, Slide 7

Bond Graphs: Example ETH Zürich Departement of Computer Science Institute of Computational Science © Dirk Zimmer, September 2006, Slide 8

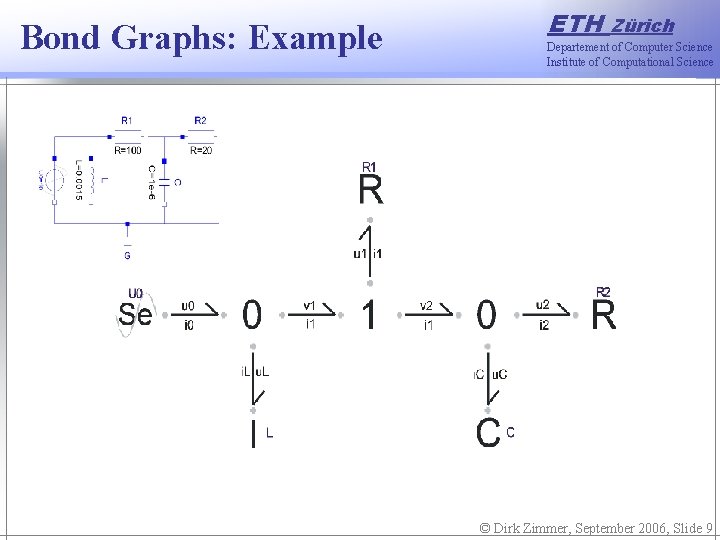
Bond Graphs: Example ETH Zürich Departement of Computer Science Institute of Computational Science © Dirk Zimmer, September 2006, Slide 9

Advantages of Bond Graphs ETH Zürich Departement of Computer Science Institute of Computational Science • Bond graphs offer a suitable balance between general usability and domain orientation. • The concepts of energy and power flows define a helpful semantic framework for bond graphs of all physical systems. • Relations can more naturally be expressed in twodimensional drawings than in one-dimensional code. © Dirk Zimmer, September 2006, Slide 10

The Bond. Lib • The Bond. Lib was presented at the Modelica Conference 2005. • Bond graphs can be composed on screen by drag and drop. • The resulting models can be directly simulated. • The library offers applicationspecific solutions for: – electrical systems – hydraulic components ETH Zürich Departement of Computer Science Institute of Computational Science © Dirk Zimmer, September 2006, Slide 11

ETH Multi. Bond Graphs Zürich Departement of Computer Science Institute of Computational Science • Multi-bond graphs are a vectorial extension of the regular bond graphs. • A multi-bond contains a freely selectable number of regular bonds of identical or similar domains. fx vx fy vy t } f 3 v Composition of a multi-bond for planar mechanics • All bond graph component models are adjusted in a suitable fashion. © Dirk Zimmer, September 2006, Slide 12

The Multi. Bond. Lib ETH Zürich Departement of Computer Science Institute of Computational Science The Multi. Bond. Lib is a free Modelica library that enables the convenient modeling of multi-bond graphs. • The library can be used for the modeling of multidimensional physical systems. • Hence, possible fields of application are: – 2 D and 3 D mechanical systems – multidimensional heat distribution – chemical reaction dynamics – general relativity © Dirk Zimmer, September 2006, Slide 13

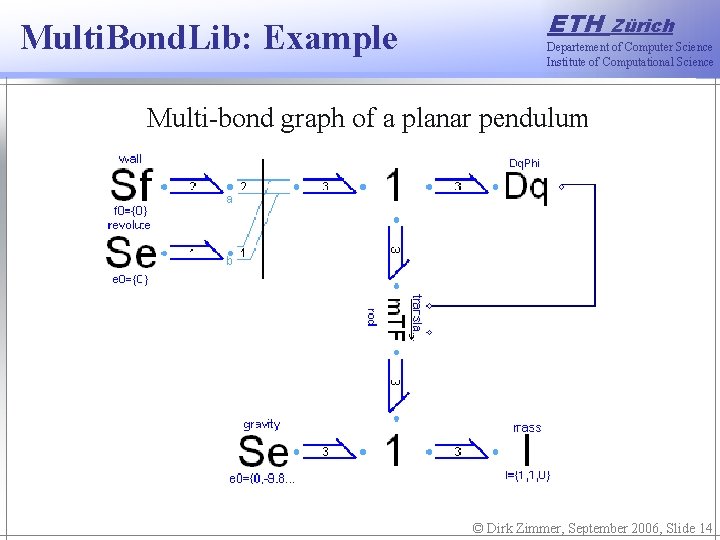
Multi. Bond. Lib: Example ETH Zürich Departement of Computer Science Institute of Computational Science Multi-bond graph of a planar pendulum © Dirk Zimmer, September 2006, Slide 14

Wrapping: Example ETH Zürich Departement of Computer Science Institute of Computational Science The process of wrapping is illustrated by means of a free crane crab: © Dirk Zimmer, September 2006, Slide 15

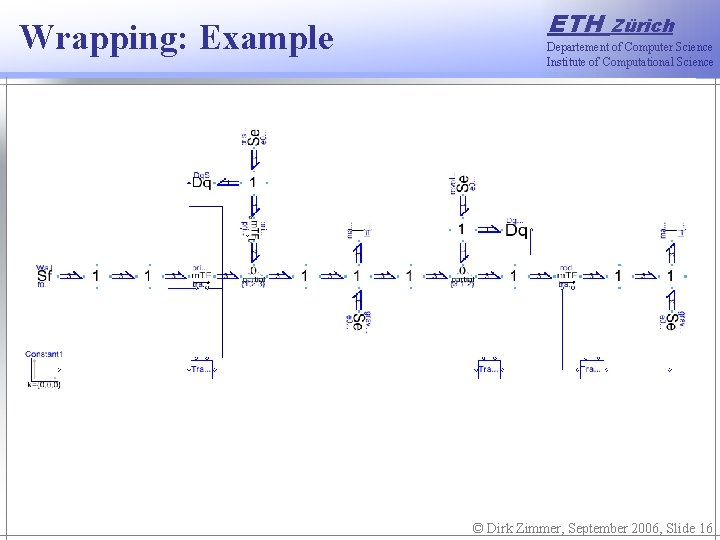
Wrapping: Example ETH Zürich Departement of Computer Science Institute of Computational Science © Dirk Zimmer, September 2006, Slide 16

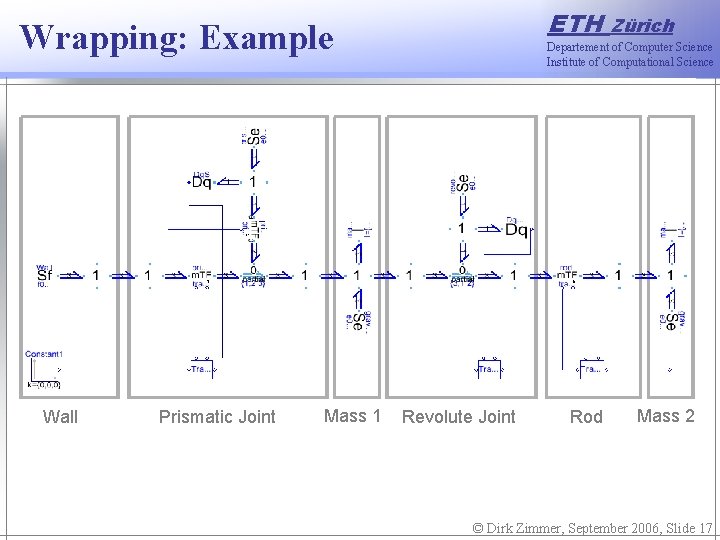
ETH Wrapping: Example Wall Prismatic Joint Mass 1 Zürich Departement of Computer Science Institute of Computational Science Revolute Joint Rod Mass 2 © Dirk Zimmer, September 2006, Slide 17

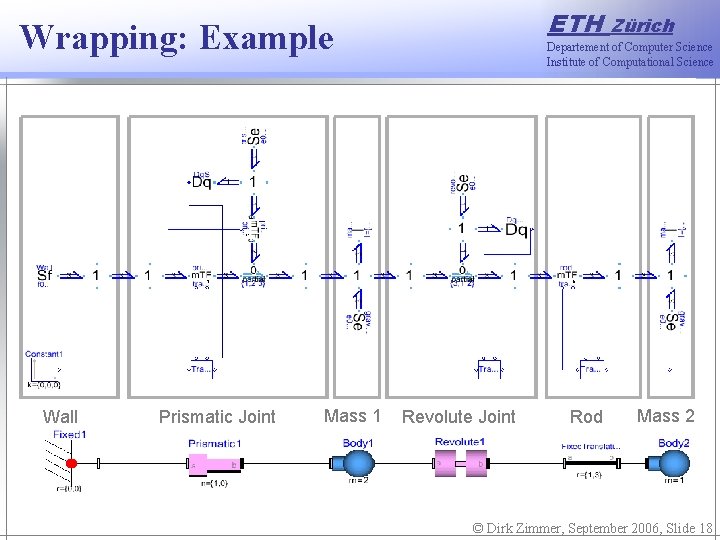
ETH Wrapping: Example Wall Prismatic Joint Mass 1 Zürich Departement of Computer Science Institute of Computational Science Revolute Joint Rod Mass 2 © Dirk Zimmer, September 2006, Slide 18

Wrapping: Example ETH Zürich Departement of Computer Science Institute of Computational Science Wrapping combines the best of two worlds: • On the upper mechanical layer, an intuitive and simply usable interface is being offered. • The lower multi-bond graph layer offers a meaningful graphical interpretation. This reduces the semantic distance from the lowest graphical layer down to the equation layer. © Dirk Zimmer, September 2006, Slide 19

Mechanical sub-libraries ETH Zürich Departement of Computer Science Institute of Computational Science • The Multi. Bond. Lib provides sub-libraries for planar and 3 D mechanical systems. The elements are based on wrapped multi-bond graphs. • All mechanical components are represented by meaningful icons. They can be configured by means of parameter menus and feature a suitable animation. • Kinematic loops are handled automatically. State variables can be manually selected if the automatic selection appears to be inappropriate. © Dirk Zimmer, September 2006, Slide 20

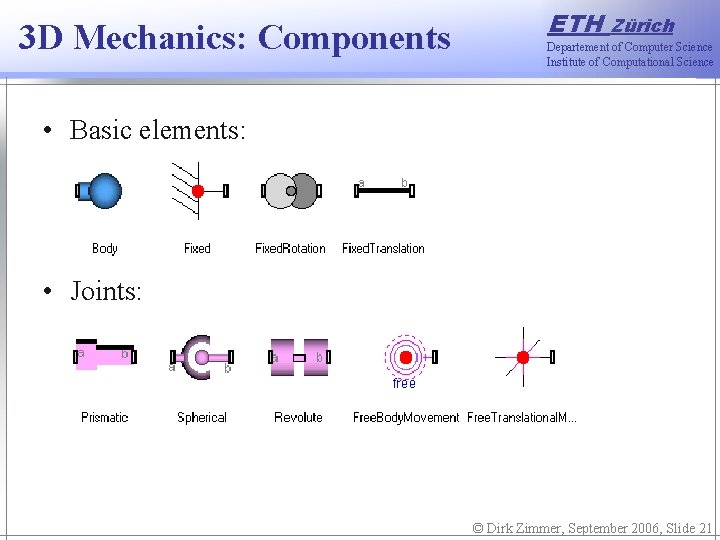
3 D Mechanics: Components ETH Zürich Departement of Computer Science Institute of Computational Science • Basic elements: • Joints: © Dirk Zimmer, September 2006, Slide 21

3 D Mechanics: Components ETH Zürich Departement of Computer Science Institute of Computational Science • Force elements: • Ideal rolling objects: © Dirk Zimmer, September 2006, Slide 22

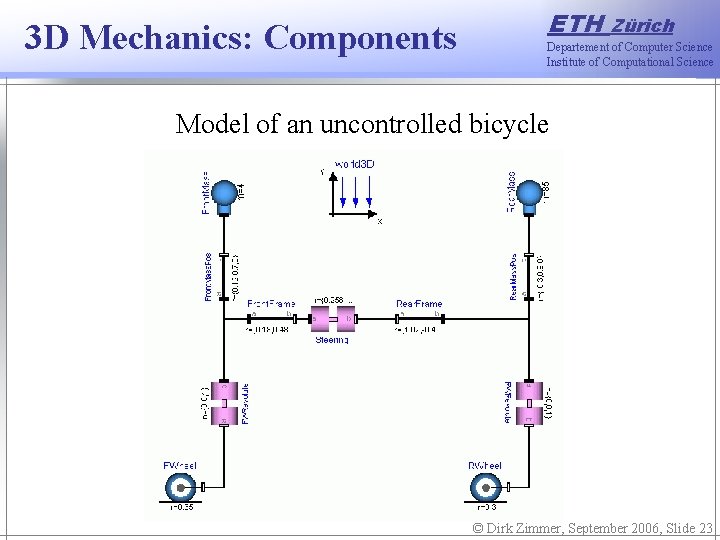
3 D Mechanics: Components ETH Zürich Departement of Computer Science Institute of Computational Science Model of an uncontrolled bicycle © Dirk Zimmer, September 2006, Slide 23

ETH 3 D Mechanics: Example 1 Translation: • • • Front. Revolute. phi Rear. Wheel. phi[1] Rear. Wheel. phi[2] Rear. Wheel. phi[3] Rear. Wheel. phi_d[1] Rear. Wheel. phi_d[2] Rear. Wheel. phi_d[3] Rear. Wheel. x. A Rear. Wheel. x. B Steering. phi Zürich Departement of Computer Science Institute of Computational Science Animation Window: Systems of 3 and 17 linear equations 1 non-linear equation Simulation 20 sec, 2500 output points 213 integration steps. 0. 7 s CPU-Time © Dirk Zimmer, September 2006, Slide 24

ETH 3 D Mechanics: Example 1 Translation: • • • Front. Revolute. phi Rear. Wheel. phi[1] Rear. Wheel. phi[2] Rear. Wheel. phi[3] Rear. Wheel. phi_d[1] Rear. Wheel. phi_d[2] Rear. Wheel. phi_d[3] Rear. Wheel. x. A Rear. Wheel. x. B Steering. phi Zürich Departement of Computer Science Institute of Computational Science Animation Window: Systems of 3 and 17 linear equations 1 non-linear equation Simulation 20 sec, 2500 output points 213 integration steps. 0. 7 s CPU-Time © Dirk Zimmer, September 2006, Slide 25

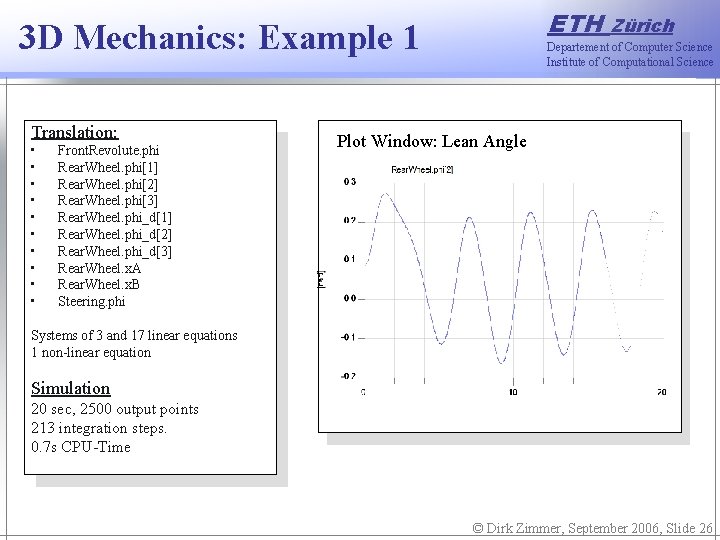
ETH 3 D Mechanics: Example 1 Translation: • • • Front. Revolute. phi Rear. Wheel. phi[1] Rear. Wheel. phi[2] Rear. Wheel. phi[3] Rear. Wheel. phi_d[1] Rear. Wheel. phi_d[2] Rear. Wheel. phi_d[3] Rear. Wheel. x. A Rear. Wheel. x. B Steering. phi Zürich Departement of Computer Science Institute of Computational Science Plot Window: Lean Angle Systems of 3 and 17 linear equations 1 non-linear equation Simulation 20 sec, 2500 output points 213 integration steps. 0. 7 s CPU-Time © Dirk Zimmer, September 2006, Slide 26

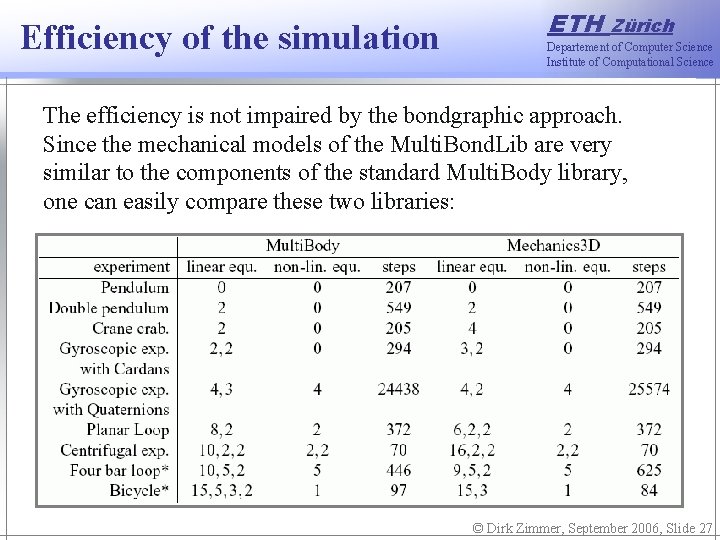
Efficiency of the simulation ETH Zürich Departement of Computer Science Institute of Computational Science The efficiency is not impaired by the bondgraphic approach. Since the mechanical models of the Multi. Bond. Lib are very similar to the components of the standard Multi. Body library, one can easily compare these two libraries: © Dirk Zimmer, September 2006, Slide 27

Further Achievements • Another sub-library contains an extension of the continuous models to hybrid models. These models allow discrete changes of motion to happen as they occur in hard collisions. • Various kinds of impacts can be modeled. Impacts can also act on kinematic loops. ETH Zürich Departement of Computer Science Institute of Computational Science © Dirk Zimmer, September 2006, Slide 28

Conclusions ETH Zürich Departement of Computer Science Institute of Computational Science • The Multi. Bond. Lib provides a general solution for the multibondgraphic modeling of physical systems. • The wrapping technique enables us to handle larger bond graphs. • The wrapped mechanical components enable a convenient object-oriented modeling of 2 D- and 3 D-mechanical systems including animation. • Multi-bond graphs lead to an intuitive, yet efficient description of mechanical systems. © Dirk Zimmer, September 2006, Slide 29

The End