The MichaelisMenten Equation ET E ES v Vmax

The Michaelis-Menten Equation ET = E + ES v= Vmax = k 2 ET v/Vmax = k 2 ES / k 2 ET = ES/ ET v/Vmax = ES/ E + ES ¿How to know ES? This equation cannot be explicitly integrated, however, without simplifying assumptions, two possibilities are: 1. Assumption of equilibrium. Leonor Michaelis and Maud Menten, building on the work of Victor Henri, assumed that k-1 » k 2, so that the first step of the reaction reaches equilibrium. ES = E * S / Ks Ks is the dissociation constant of the first step in the enzymatic reaction

The Michaelis-Menten Equation 1. Assumption of steady-state. Figure illustrates the progress curves of the various participants in reaction under the physiologically common conditions that substrate is in great excess over Enzyme ([S] » [E]). ES maintains a steady state and [ES] can be treated as having a constant value: The so called steady state assumption, a more general condition that of equilibrium, was first proposed in 1925 by G. E. Briggs and B. S. Haldane

The Michaelis-Menten Equation Solving for [ES]: ES = E * S /(k-1+k 2)/k 1 The Michaelis constant, KM , is defined as Therefore: ES = E * S / KM

The Michaelis-Menten Equation The expression of the initial velocity (v 0) of the reaction, the velocity at t=0, thereby becomes v/Vmax = ES/ (E + ES) v/Vmax = (E*S)/Km/ (E + (E*S)/Km ) v/Vmax = S/ Km / (1 + S/Km) v/Vmax = S / Km + S This expression, the Michaelis-Menten equation, is the basic equation of enzyme kinetic. The maximal velocity of a reaction, Vmax occurs at high substrate concentrations when the enzyme is saturated, that is, S>> Km, and ET is entirely in the ES form v= Vmax when

Significance of the Michaelis Constant The Michaelis constant, KM, has a simple operational definition. At the substrate concentration at which [S] = KM, this equation yields v 0 = Vmax/2 so that KM is the substrate concentration at which the reaction velocity is half maximal

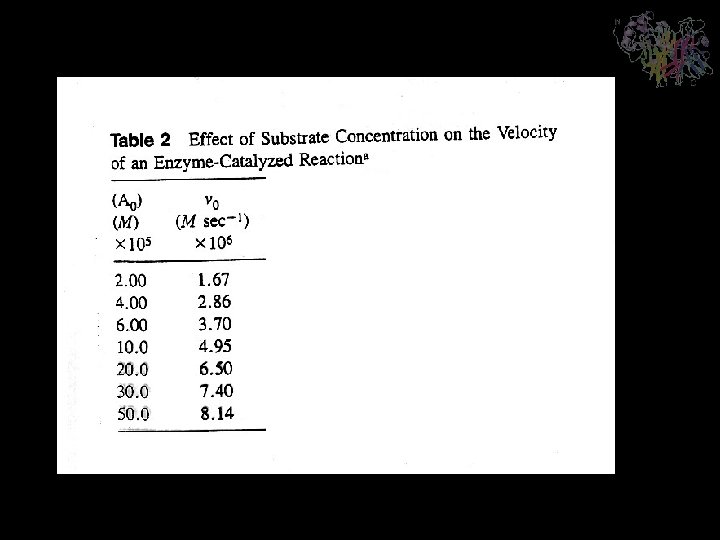
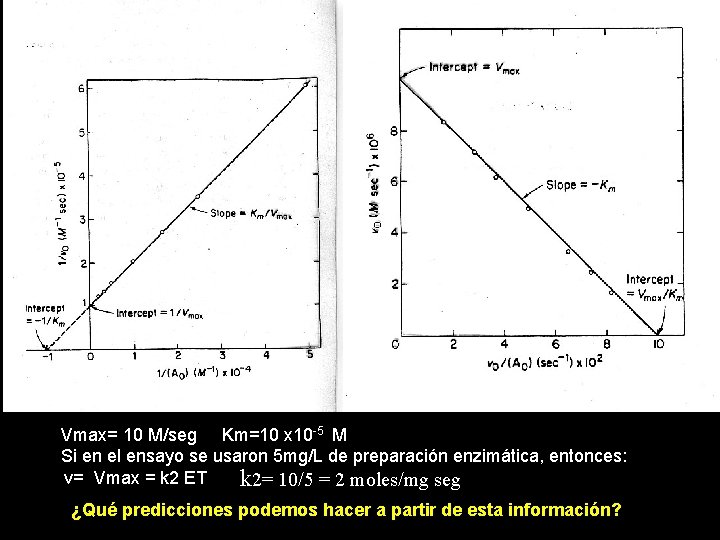
Vmax= 10 M/seg Km=10 x 10 -5 M Si en el ensayo se usaron 5 mg/L de preparación enzimática, entonces: v= Vmax = k 2 ET k 2= 10/5 = 2 moles/mg seg ¿Qué predicciones podemos hacer a partir de esta información?

Al iniciar: t = 0, S = So A cualquier tiempo: T=t S=S X = (So-S)/So - d. S/dt = vi = So d. X/dt Graficar por ejemplo : (So – S)/t vs (1/t) ln (So/S)

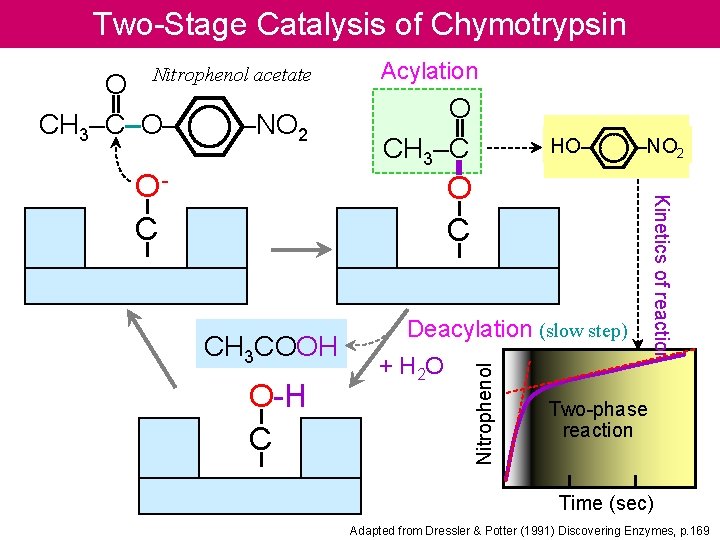
Two-Stage Catalysis of Chymotrypsin Nitrophenol acetate –NO 2 HO– –NO 2 O C CH 3 COOH O-H C Deacylation (slow step) + H 2 O Kinetics of reaction OC O CH 3–C Nitrophenol O CH 3–C–O– Acylation Two-phase reaction Time (sec) Adapted from Dressler & Potter (1991) Discovering Enzymes, p. 169

DESVIACIONESA M&M d. E/dt = -k 1 E*S + k-1 ES + k 3 ES’ d. ES/dt = k 1 E*S – ES (k-1 + k 2) d. ES’/dt = k 2 ES – k 3 ES’ v = d. P 1/dt = k 2 ES v = d. P 2/dt = k 3 ES’ ET= E + ES’ d. P 2/dt = v = k 3 ES’ v = k 3 k 2 ES / k 3 v = k 2 k 1 E*S / (k-1 + k 2) From the steady state assumption: : d. E/dt = 0 -k 1 E*S + k-1 ES + k 3 ES’ d. ES/dt = 0 ES = k 1 E*S / (k-1 + k 2) d. ES’/dt = 0 ES’ = k 2 ES / k 3 Vmax = k 3 ET Vmax = k 3 (E + ES’) Vmax = k 3 (E + k 1 E*S / (k-1 + k 2) + k 2 ES / k 3 Vmax = k 3 (E + k 1 E*S / (k-1 + k 2) + k 2 k 1 E*S / (k-1 + k 2) / k 3 ) Vmax = k 3 E + k 1 k 3 E*S / (k-1 + k 2) + k 2 k 1 E*S / (k-1 + k 2)

v / Vmax = k 2 k 1 E*S / (k-1 + k 2) k 3 E + k 1 k 3 E*S / (k-1 + k 2) + k 2 k 1 E*S / (k-1 + k 2) v / Vmax = k 2 k 1 S k 3 (k-1 + k 2) + k 1 k 3 S + k 2 k 1 S v / Vmax = k 2 k 1 S k 3 (k-1 + k 2) + k 1 S (k 2 + k 3) v / Vmax = k 2 S / (k 2 + k 3) k 3 (k-1 + k 2) / (k 2 + k 3) + k 1 S = k 2 k 3 ET S / (k 2 + k 3) k 3 (k-1 + k 2) / (k 2 + k 3) + k 1 S v Vmax = k 3 ET

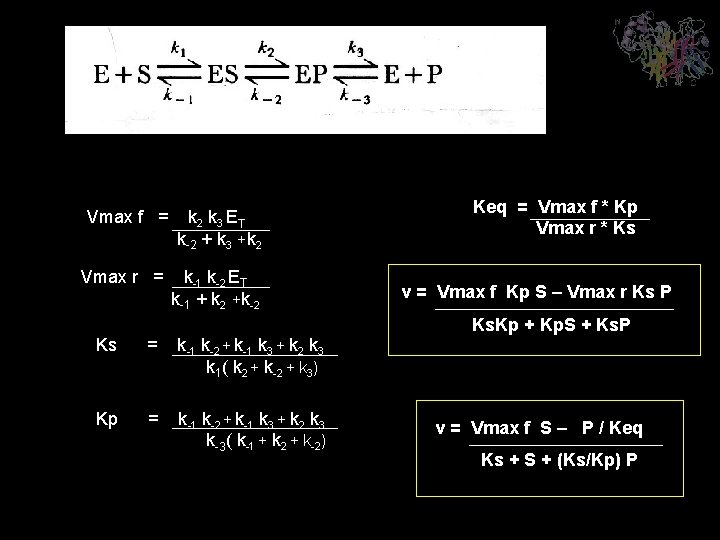
K-2+ Vmax f = k 2 k 3 ET k-2 + k 3 +k 2 Vmax r = k-1 k-2 ET k-1 + k 2 +k-2 Keq = Vmax f * Kp Vmax r * Ks v = Vmax f Kp S – Vmax r Ks P Ks. Kp + Kp. S + Ks. P Ks = k-1 k-2 + k-1 k 3 + k 2 k 3 k 1( k 2 + k-2 + k 3) Kp = k-1 k-2 + k-1 k 3 + k 2 k 3 k-3( k-1 + k 2 + k-2) v = Vmax f S – P / Keq Ks + S + (Ks/Kp) P