The Method of Multiplicities Madhu Sudan Microsoft New

The Method of Multiplicities Madhu Sudan Microsoft New England/MIT Based on joint works with: • V. Guruswami ‘ 98 • S. Saraf ‘ 08 • Z. Dvir, S. Kopparty, S. Saraf ‘ 09 June 13 -18, 2011 Mutliplicities @ CSR 1

Agenda n A technique for combinatorics, via algebra: n Polynomial (Interpolation) Method + Multiplicity method n List-decoding of Reed-Solomon Codes n Bounding size of Kakeya Sets n Extractor constructions n (won’t cover) Locally decodable codes June 13 -18, 2011 Mutliplicities @ CSR 2 of 33

Part I: Decoding Reed-Solomon Codes n Reed-Solomon Codes: n Commonly used codes to store information (on CDs, DVDs etc. ) n Message: C 0, C 1, …, Cd є F (finite field) n Encoding: d C xi n View message as polynomial: M(x) = i=0 i n n Encoding = evaluations: { M(®) }_{ ® є F } Decoding Problem: n Given: (x 1, y 1) … (xn, yn) є F x F; integers t, d; n Find: deg. d poly through t of the n points. June 13 -18, 2011 Mutliplicities @ CSR 3 of 33

List-decoding? n n If #errors (n-t) very large, then several polynomials may agree with t of n points. n List-decoding problem: n Report all such polynomials. n Combinatorial obstacle: n There may be too many such polynomials. n Hope – can’t happen. n To analyze: Focus on polynomials P 1, …, PL and set of agreements S 1 … SL. Combinatorial question: Can S 1, … SL be large, while n = | [j Sj | is small? June 13 -18, 2011 Mutliplicities @ CSR 4 of 33

List-decoding of Reed-Solomon codes n n Given L polynomials P 1, …, PL of degree d; and sets S 1, …, SL ½ F £ F s. t. n |S i | = t n Si ½ {(x, Pi(x)) | x 2 F} n How small can n = |S| be, where S = [i Si ? Algebraic analysis from [S. ‘ 96, Guruswami. S ’ 98] basis of decoding algorithms. June 13 -18, 2011 Mutliplicities @ CSR 5 of 33

List-decoding analysis [S ‘ 96] n n n Construct Q(x, y) ≠ 0 s. t. n Degy(Q) < L n Degx(Q) < n/L n Q(x, y) = 0 for every (x, y) 2 S = [i Si Can Show: n Such a Q exists (interpolation/counting). n Implies: t > n/L + d. L ) (y – Pi(x)) | Q Conclude: n ¸ L¢ (t – d. L). n (Can be proved combinatorially also; using inclusion-exclusion) n If L > t/(2 d), yield n ¸ t 2/(4 d) June 13 -18, 2011 Mutliplicities @ CSR 6 of 33

Focus: The Polynomial Method n To analyze size of “algebraically nice” set S: n Find polynomial Q vanishing on S; n (Can prove existence of Q by counting coefficients … degree Q grows with |S|. ) n Use “algebraic niceness” of S to prove Q vanishes at other places as well. n (In our case whenever y = Pi(x) ). n Conclude Q zero too often (unless S large). … June 13 -18, 2011 (abstraction based on [Dvir]’s work) Mutliplicities @ CSR 7 of 33

Improved L-D. Analysis [G. +S. ‘ 98] n n n Can we improve on the inclusion-exclusion bound? One that works when n > t 2/(4 d)? Idea: Try fitting a polynomial Q that passes through each point with “multiplicity” 2. n Can find with Degy < L, Degx < 3 n/L. n If 2 t > 3 n/L + d. L then (y-Pi(x)) | Q. n Yields n ¸ (L/3). (2 t – d. L) n If L>t/d, then n ¸ t 2/(3 d). Optimizing Q; letting mult. 1, get n ¸ t 2/d June 13 -18, 2011 Mutliplicities @ CSR 8 of 33

Aside: Is the factor of 2 important? n n Results in some improvement in [GS] (allowed us to improve list-decoding for codes of high rate) … But crucial to subsequent work n [Guruswami-Rudra] construction of rateoptimal codes: Couldn’t afford to lose this factor of 2 (or any constant > 1). June 13 -18, 2011 Mutliplicities @ CSR 9 of 33

Focus: The. Multiplicity. Method n To analyze size of “algebraically nice” set S: n Find poly Q zero on S (w. high multiplicity); n (Can prove existence of Q by counting coefficients … degree Q grows with |S|. ) n Use “algebraic niceness” of S to prove Q vanishes at other places as well. n (In our case whenever y = Pi(x) ). n Conclude Q zero too often (unless S large). June 13 -18, 2011 Mutliplicities @ CSR 10 of 33

Multiplicity = ? n n Over reals: Q(x, y) has root of multiplicity m+1 at (a, b) if every partial derivative of order up to m vanishes at 0. Over finite fields? n Derivatives don’t work; but “Hasse derivatives” do. What are these? Later… n There are {m+n choose n} such derivatives, for n-variate polynomials; n Each is a linear function of coefficients of f. June 13 -18, 2011 Mutliplicities @ CSR 11 of 33

Part II: Kakeya Sets June 13 -18, 2011 Mutliplicities @ CSR 12 of 33

Kakeya Sets n n K ½ Fn is a Kakeya set if it has a line in every direction. n I. e. , 8 y 2 Fn 9 x 2 Fn s. t. {x + t. y | t 2 F} ½ K n F is a field (could be Reals, Rationals, Finite). Our Interest: n F = Fq (finite field of cardinality q). n Lower bounds. n Simple/Obvious: qn/2 · K · qn n Do better? Mostly open till [Dvir 2008]. June 13 -18, 2011 Mutliplicities @ CSR 13 of 33

Kakeya Set analysis [Dvir ‘ 08] n n Find Q(x 1, …, xn) ≠ 0 s. t. n Total deg. of Q < q (let deg. = d) n Q(x) = 0 for every x 2 K. (exists if |K| < qn/n!) Prove that (homogenous deg. d part of) Q vanishes on y, if there exists a line in direction y that is contained in K. n Line L ½ K ) Q|L = 0. n Highest degree coefficient of Q|L is homogenous part of Q evaluated at y. Conclude: homogenous part of Q = 0. ><. Yields |K| ¸ qn/n!. June 13 -18, 2011 Mutliplicities @ CSR 14 of 33

Multiplicities in Kakeya [Saraf, S ’ 08] n n Fit Q that vanishes often? n Good choice: #multiplicity m = n n Can find Q ≠ 0 of individual degree < q, that vanishes at each point in K with multiplicity n, provided |K| 4 n < qn n Q|L is of degree < qn. n But it vanishes with multiplicity n at q points! n So it is identically zero ) its highest degree coeff. is zero. >< Conclude: |K| ¸ (q/4)n June 13 -18, 2011 Mutliplicities @ CSR 15 of 33

Comparing the bounds n n n Simple: |K| ¸ qn/2 [Dvir]: |K| ¸ qn/n! [SS]: |K| ¸ qn/4 n [SS] improves Simple even when q (large) constant and n 1 (in particular, allows q < n) [Mockenhaupt. Tao, Dvir]: 9 K s. t. |K| · qn/2 n-1 + O(qn-1) Can we do even better? June 13 -18, 2011 Mutliplicities @ CSR 16 of 33

Part III: Randomness Mergers & Extractors June 13 -18, 2011 Mutliplicities @ CSR 17 of 33

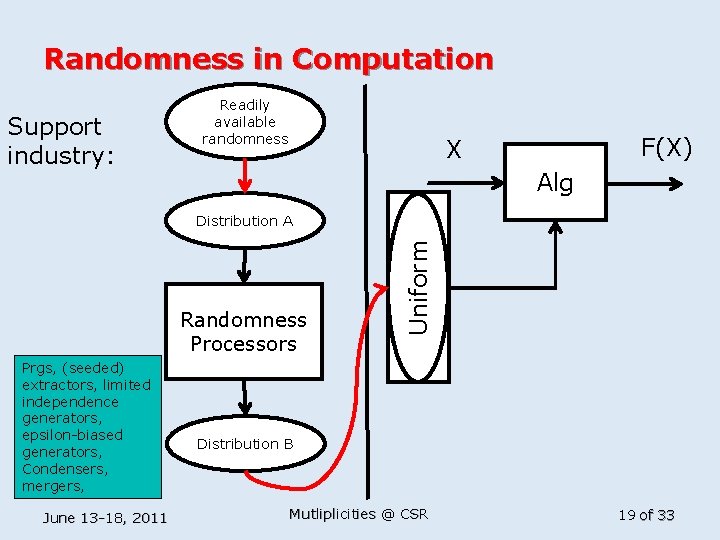
Context n n One of the motivations for Dvir’s work: n Build better “randomness extractors” n Approach proposed in [Dvir-Shpilka] n Following [Dvir] , new “randomness merger” and analysis given by [Dvir-Wigderson] n Led to “extractors” matching known constructions, but not improving them … What are Extractors? Mergers? … can we improve them? June 13 -18, 2011 Mutliplicities @ CSR 18 of 33

Randomness in Computation Support industry: Readily available randomness F(X) X Alg Randomness Processors Prgs, (seeded) extractors, limited independence generators, epsilon-biased generators, Condensers, mergers, June 13 -18, 2011 Uniform Random Distribution A Distribution B Mutliplicities @ CSR 19 of 33

Randomness Extractors and Mergers n Extractors: n Dirty randomness (Biased, correlated) + small pure seed n Pure randomness (Uniform, independent … nearly) Mergers: General primitive useful in the context of manipulating randomness. n k random variables (One of them uniform) 1 random variable (high entropy) (Don’t know which, others potentially correlated) + small pure seed June 13 -18, 2011 Mutliplicities @ CSR 20 of 33

Merger Analysis Problem n n n Merger(X 1, …, Xk; s) = f(s), where X 1, …, Xk 2 Fqn; s 2 Fq and f is deg. k-1 function mapping F Fn s. t. f(i) = Xi. (f is the curve through X 1, …, Xk) Question: For what choices of q, n, k is Merger’s output close to uniform? Arises from [Dvir. Shpilka’ 05, Dvir. Wigderson’ 08]. n “Statistical high-deg. version” of Kakeya problem. June 13 -18, 2011 Mutliplicities @ CSR 21 of 33

Concerns from Merger Analysis n n [DW] Analysis: Worked only if q > n. n So seed length = log 2 q > log 2 n n Not good enough for setting where k = O(1), and n 1. n (Would like seed length to be O(log k)). Multiplicity technique: n seems bottlenecked at mult = n. June 13 -18, 2011 Mutliplicities @ CSR 22 of 33

General obstacle in multiplicity method n n Can’t force polynomial Q to vanish with too high a multiplicity. Gives no benefit. E. g. Kakeya problem: Why stop at mult = n? n Most we can hope from Q is that it vanishes on all of qn; n Once this happens, Q = 0, if its degree is < q in each variable. n So Q|L is of degree at most qn, so mult n suffices. Using larger multiplicity can’t help! n Or can it? June 13 -18, 2011 Mutliplicities @ CSR 23 of 33

Extended method of multiplicities n (In Kakeya context): n Perhaps vanishing of Q with high multiplicity at each point shows higher degree polynomials (deg > q in each variable) are identically zero? n (Needed: Condition on multiplicity of zeroes of multivariate polynomials. ) n Perhaps Q can be shown to vanish with high multiplicity at each point in Fn. n (Technical question: How? ) June 13 -18, 2011 Mutliplicities @ CSR 24 of 33

Vanishing of high-degree polynomials n n n Mult(Q, a) = multiplicity of zeroes of Q at a. I(Q, a) = 1 if mult(Q, a) > 0 and 0 o. w. = min{1, mult(Q, a)} Schwartz-Zippel: for any S ½ F I(Q, a) · d. |S|n-1 where sum is over a 2 Sn Can we replace I with mult above? Would strengthen S-Z, and be useful in our case. [DKSS ‘ 09]: Yes … (simple inductive proof … that I can never remember) June 13 -18, 2011 Mutliplicities @ CSR 25 of 33

Multiplicities? n n Q(X 1, …, Xn) has zero of mult. m at a = (a 1, …, an) if all (Hasse) derivatives of order < m vanish. Hasse derivative = ? n Formally defined in terms of coefficients of Q, various multinomial coefficients and a. n But really … n The i = (i 1, …, in)th derivative is the coefficient of z 1 i 1…znin in Q(z + a). n Even better … coeff. of zi in Q(z+x) n (defines ith derivative Qi as a function of x; can evaluate at x = a). June 13 -18, 2011 Mutliplicities @ CSR 26 of 33

Key Properties n n n Each derivative is a linear function of coefficients of Q. [Used in [GS’ 98], [SS’ 09]. ] (Q+R)i = Qi + Ri Q has zero of mult m at a, and S is a curve that passes through a, then Q|S has zero of mult m at a. [Used for lines in prior work. ] Qi is a polynomial of degree deg(Q) - j ii (not used in prior works) (Qi)j ≠ Qi+j, but Qi+j(a) = 0 ) (Qi)j(a) = 0 Q vanishes with mult m at a ) Qi vanishes with mult m - j ii at a. June 13 -18, 2011 Mutliplicities @ CSR 27 of 33

Propagating multiplicities (in Kakeya) n n Find Q that vanishes with mult m on K For every i of order m/2, Q_i vanishes with mult m/2 on K. Conclude: Q, as well as all derivatives of Q of order m/2 vanish on Fn ) Q vanishes with multiplicity m/2 on Fn Next Question: When is a polynomial (of deg > qn, or even qn) that vanishes with high multiplicity on qn identically zero? June 13 -18, 2011 Mutliplicities @ CSR 28 of 33

Back to Kakeya n Find Q of degree d vanishing on K with mult m. (can do if (m/n)n |K| < (d/n)n , dn > mn |K| ) Conclude Q vanishes on Fn with mult. m/2. Apply Extended-Schwartz-Zippel to conclude (m/2) qn < d qn-1 , (m/2) q < d , (m/2)n qn < dn = mn |K| n Conclude: |K| ¸ (q/2)n n Tight to within 2+o(1) factor! n n June 13 -18, 2011 Mutliplicities @ CSR 29 of 33

Consequences for Mergers n n Can analyze [DW] merger when q > k very small, n growing; n Analysis similar, more calculations. n Yields: Seed length log q (independent of n). By combining it with every other ingredient in extractor construction: n Extract all but vanishing entropy (k – o(k) bits of randomness from (n, k) sources) using O(log n) seed (for the first time). June 13 -18, 2011 Mutliplicities @ CSR 30 of 33

Other applications n n n [Woodruff-Yekhanin ‘ 05]: An elegant construction of novel “LDCs (locally decodable codes)”. [Outclassed by more recent Yekhanin/Efremenko constructions. ] [Kopparty-Lev-Saraf-S. ‘ 09]: Higher dimensional Kakeya problems. [Kopparty-Saraf-Yekhanin ‘ 2011]: Locally decodable codes with Rate 1. June 13 -18, 2011 Mutliplicities @ CSR 32 of 33

Conclusions n n n New (? ) technique in combinatorics … Polynomial method + Multiplicity method n Supporting evidence: n List decoding n Kakeya sets n Extractors/Mergers n Locally decodable codes … More? June 13 -18, 2011 Mutliplicities @ CSR 33 of 33

Thank You June 13 -18, 2011 Mutliplicities @ CSR 34