The mechanism of the dielectric relaxation in ice

The mechanism of the dielectric relaxation in ice and water

Forty-one Anomalies of Water 1 The anomalies 1. Water has unusually high melting point. 2. Water has unusually high boiling point. 3. Water has unusually high critical point. [explanation] 4. Water has unusually high surface tension and can bounce. [explanation] 5. Water has unusually high viscosity. [explanation] 6. Water has unusually high heat of vaporization. [explanation] 7. Water shrinks on melting. 8. Water has a high density that increases on heating (up to 3. 984°C). [explanation] 9. The number of nearest neighbors increases on melting. [explanation] 10. The number of nearest neighbors increases with temperature. [explanation] 11. Pressure reduces its melting point (13. 35 MPa gives a melting point of -1°C) [explanation] 12. Pressure reduces the temperature of maximum density. [explanation] 13. D 2 O and T 2 O differ from H 2 O in their physical properties much more than might be expected from their increased mass; e. g. they have increasing temperatures of maximum density (11. 185°C and 13. 4°C respectively). [explanation] 14. Water shows an unusually large viscosity increase but diffusion decrease as the temperature is lowered. [explanation] 15. Water's viscosity decreases with pressure (at temperatures below 33°C). [explanation] 16. Water has unusually low compressibility. [explanation] 17. The compressibility drops as temperature increases down to a minimum at about 46. 5°C. Below this temperature, water is easier to compress as the temperature is lowered. [explanation] 18. Water has a low coefficient of expansion (thermal expansivity). [explanation] 19. Water's thermal expansivity reduces increasingly (becoming negative) at low temperatures. 20. The speed of sound increases with temperature (up to a maximum at 73°C). [explanation] 21. Water has over twice the specific heat capacity of ice or steam. [explanation] 22. The specific heat capacity (CP and CV) is unusually high. [explanation] 23. Specific heat capacity; CP has a minimum and CV has maximum. [explanation] 24. NMR spin-lattice relaxation is very small at low temperatures. [explanation] 25. Solutes have varying effects on properties such as density and viscosity. [explanation] 26. None of its solutions even approach thermodynamic ideality; even D 2 O in H 2 O is not ideal. [explanation] 27. X-ray diffraction shows an unusually detailed structure. 28. Supercooled water has two phases and a second critical point at about -91°C. [explanation] 29. Liquid water may be supercooled, in tiny droplets, down to about -70°C. It may also be produced from glassy amorphous ice between -123°C and - 149°C [74] and may coexist with cubic ice up to -63°C [137]. [explanation] 30. Solid water exists in a wider variety of stable (and metastable) crystal and amorphous structures than other materials. 31. Hot water may freeze faster than cold water; the Mpemba effect. [explanation] 32. The refractive index of water has a maximum value at just below 0°C. [explanation] 33. The solubilities of non-polar gases in water decrease with temperature to a minimum and then rise. [explanation] 34. At low temperatures, the self-diffusion of water increases as the density and pressure increase. [explanation] 35. The thermal conductivity of water is high and rises to a maximum at about 130°C. [explanation] 36. Proton and hydroxide ion mobilities are anomalously fast in an electric field [explanation] 37. The heat of fusion of water with temperature exhibits a maximum at -17°C [15]. [explanation] 38. The dielectric constant is high and behaves anomalously with temperature. 39. Under high pressure water molecules move further away from each other with increasing pressure 40. The electrical conductivity of water rises to a maximum at about 230°C and then falls. 41. Warm water vibrates longer than cold water.

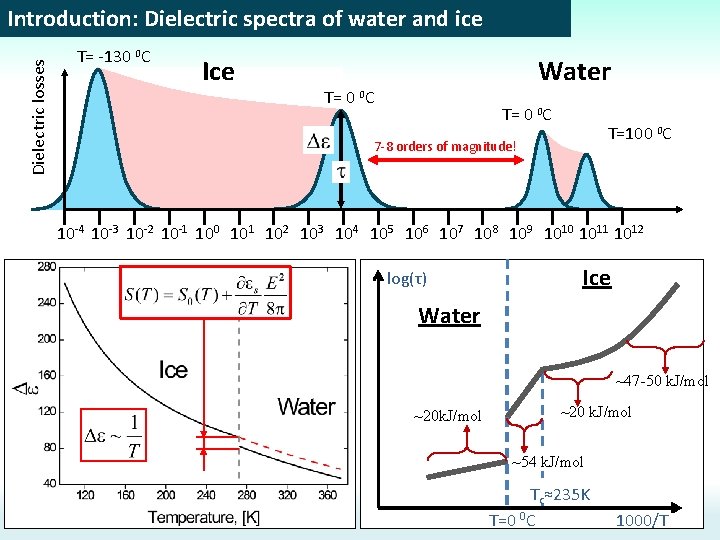
Dielectric losses Introduction: Dielectric spectra of water and ice T= -130 0 C Ice Water T= 0 0 C T=100 0 C 7 -8 orders of magnitude! 10 -4 10 -3 10 -2 10 -1 100 101 102 103 104 105 106 107 108 109 1010 1011 1012 log(τ) Ice Water ~47 -50 k. J/mol ~20 k. J/mol ~54 k. J/mol Tc≈235 K T=0 0 C 1000/T

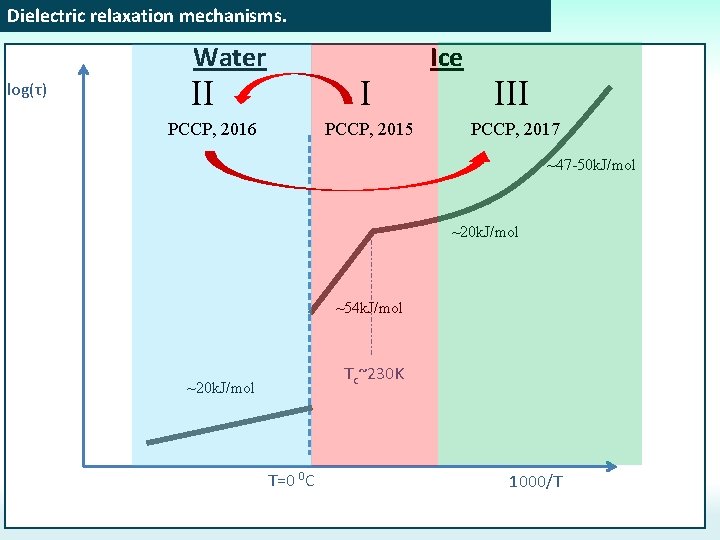
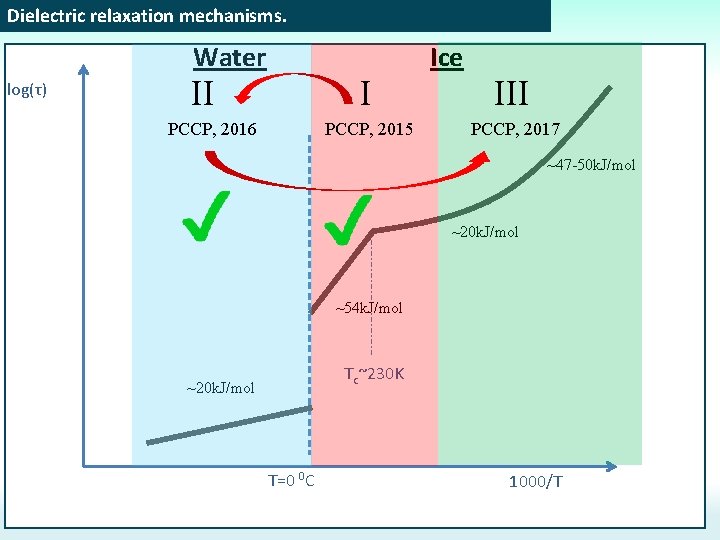
Dielectric relaxation mechanisms. Water log(τ) II I PCCP, 2016 PCCP, 2015 Ice III PCCP, 2017 ~47 -50 k. J/mol ~20 k. J/mol ~54 k. J/mol Tc~230 K ~20 k. J/mol T=0 0 C 1000/T

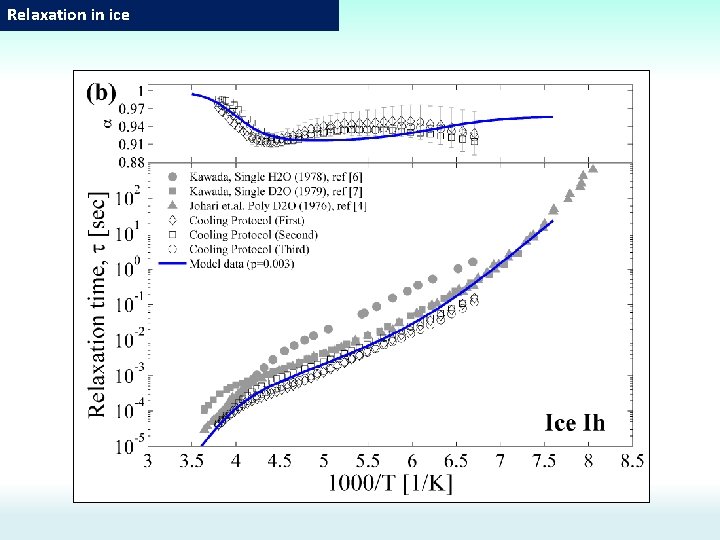
The dielectric relaxation of ice Ih (High temperature Crossover)

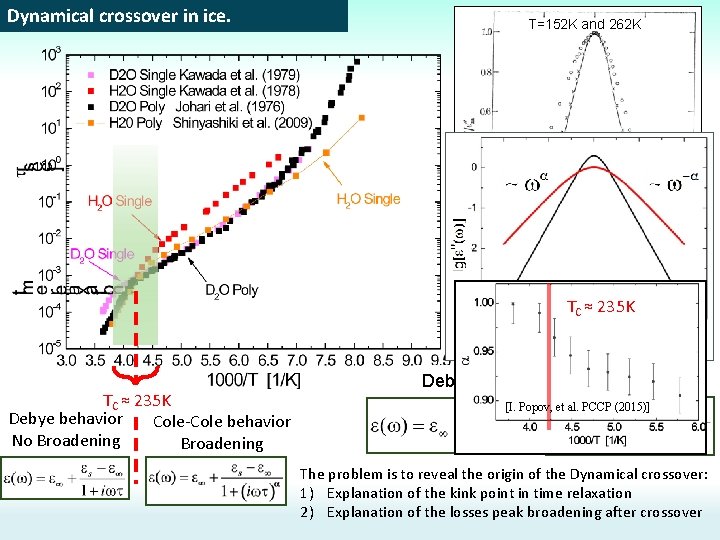
Dynamical crossover in ice. T=152 K and 262 K [G. P. Johari et al. (1981)] TC ≈ 235 K Debye behavior Cole-Cole behavior No Broadening Debye law Cole-Cole law [I. Popov, et al. PCCP (2015)] The problem is to reveal the origin of the Dynamical crossover: 1) Explanation of the kink point in time relaxation 2) Explanation of the losses peak broadening after crossover

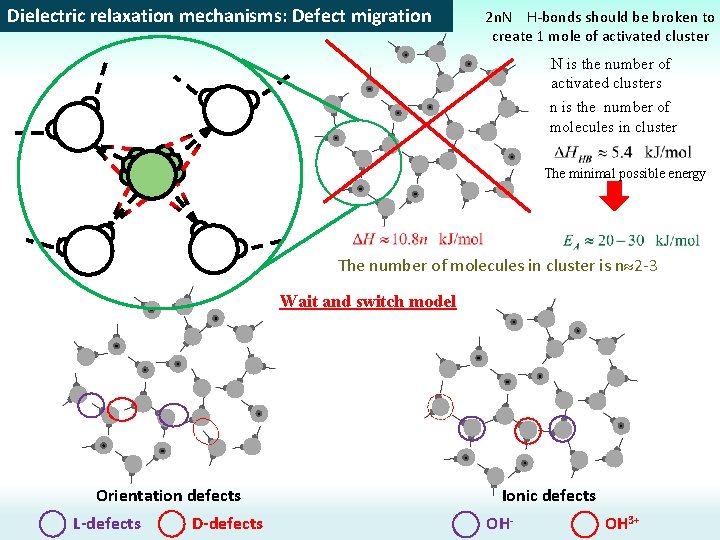
Dielectric relaxation mechanisms: Defect migration 2 n. N H-bonds should be broken to create 1 mole of activated cluster N is the number of activated clusters n is the number of molecules in cluster The minimal possible energy The number of molecules in cluster is n 2 -3 Wait and switch model Orientation defects L-defects D-defects Ionic defects OH- OH 3+

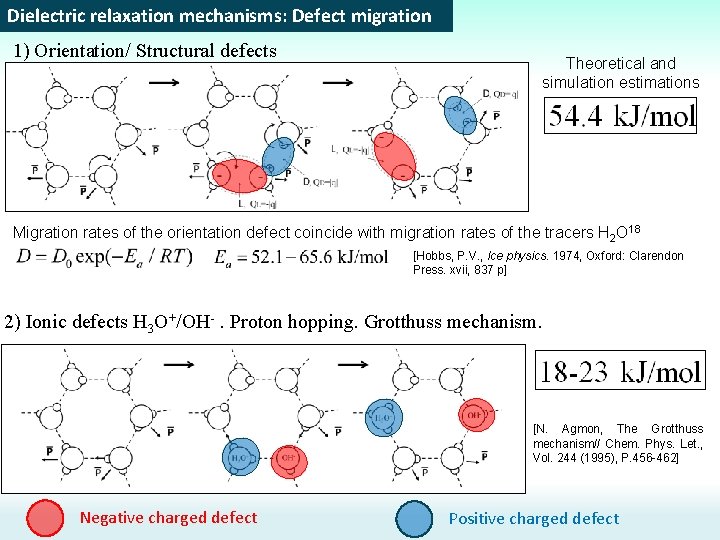
Dielectric relaxation mechanisms: Defect migration 1) Orientation/ Structural defects Theoretical and simulation estimations Migration rates of the orientation defect coincide with migration rates of the tracers H 2 O 18 [Hobbs, P. V. , Ice physics. 1974, Oxford: Clarendon Press. xvii, 837 p] 2) Ionic defects H 3 O+/OH-. Proton hopping. Grotthuss mechanism. [N. Agmon, The Grotthuss mechanism// Chem. Phys. Let. , Vol. 244 (1995), P. 456 -462] Negative charged defect Positive charged defect

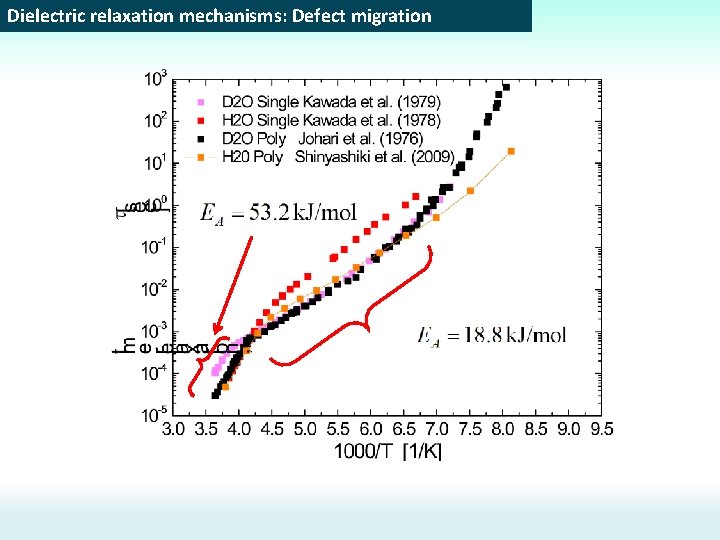
Dielectric relaxation mechanisms: Defect migration

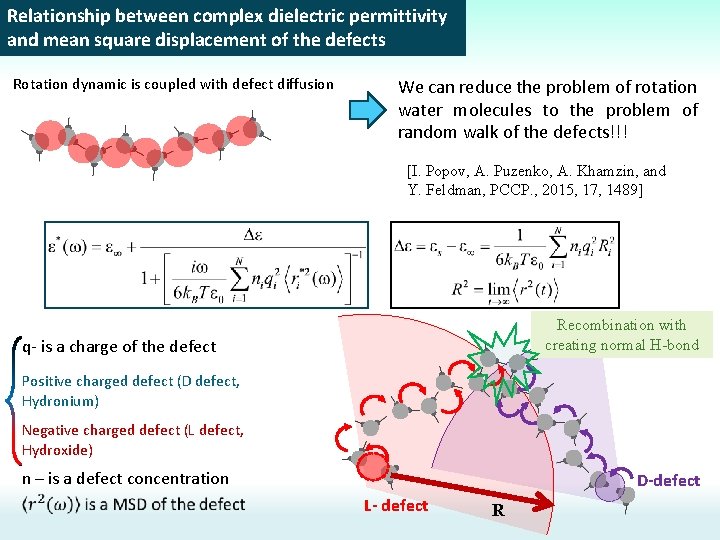
Relationship between complex dielectric permittivity and mean square displacement of the defects Rotation dynamic is coupled with defect diffusion We can reduce the problem of rotation water molecules to the problem of random walk of the defects!!! [I. Popov, A. Puzenko, A. Khamzin, and Y. Feldman, PCCP. , 2015, 17, 1489] Recombination with creating normal H-bond q- is a charge of the defect Positive charged defect (D defect, Hydronium) Negative charged defect (L defect, Hydroxide) n – is a defect concentration D-defect L- defect R

Migration of the two types of defects Anomalous diffusion Orientation defects Ionic defects Parallel relaxation channels

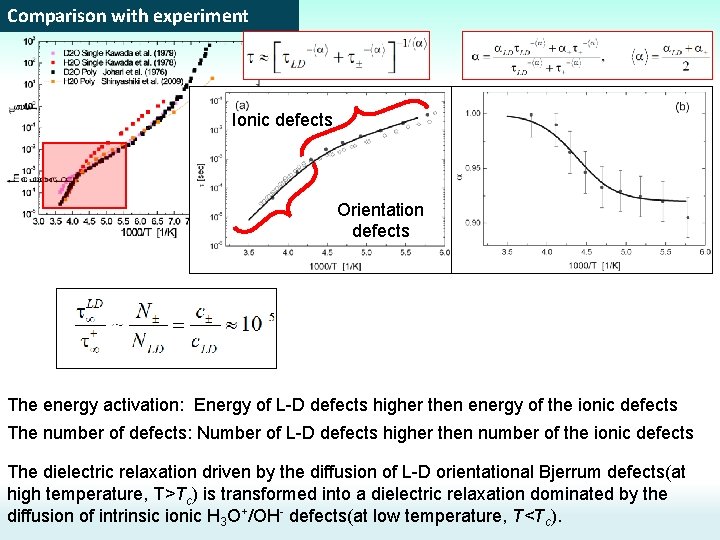
Comparison with experiment Ionic defects Orientation defects The energy activation: Energy of L-D defects higher then energy of the ionic defects The number of defects: Number of L-D defects higher then number of the ionic defects The dielectric relaxation driven by the diffusion of L-D orientational Bjerrum defects(at high temperature, T>Tc) is transformed into a dielectric relaxation dominated by the diffusion of intrinsic ionic H 3 O+/OH- defects(at low temperature, T<Tc).

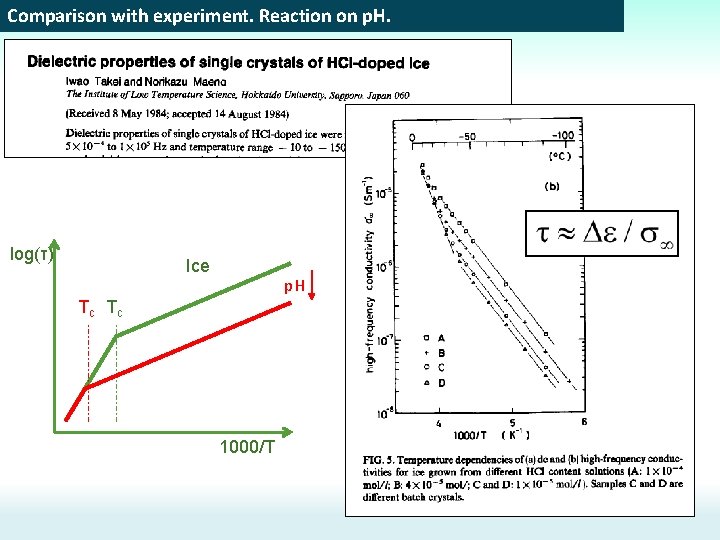
Comparison with experiment. Reaction on p. H. log(τ) Ice p. H Tc Tc 1000/T

The dielectric relaxation of water

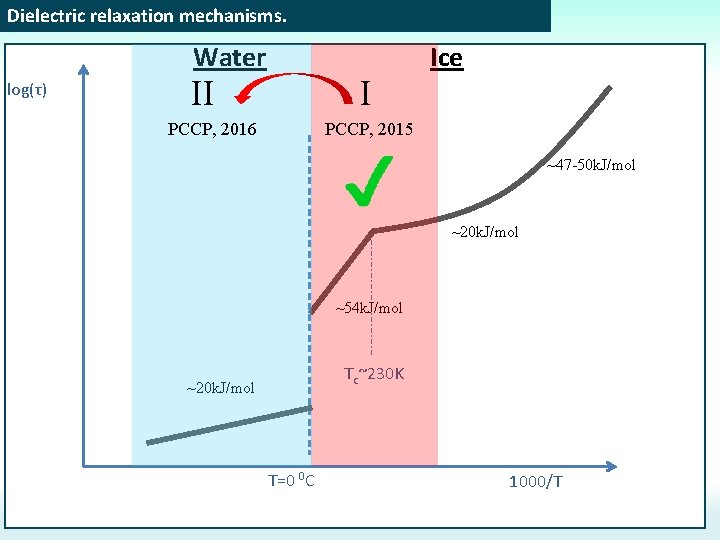
Dielectric relaxation mechanisms. Water log(τ) II I PCCP, 2016 Ice PCCP, 2015 ~47 -50 k. J/mol ~20 k. J/mol ~54 k. J/mol Tc~230 K ~20 k. J/mol T=0 0 C 1000/T

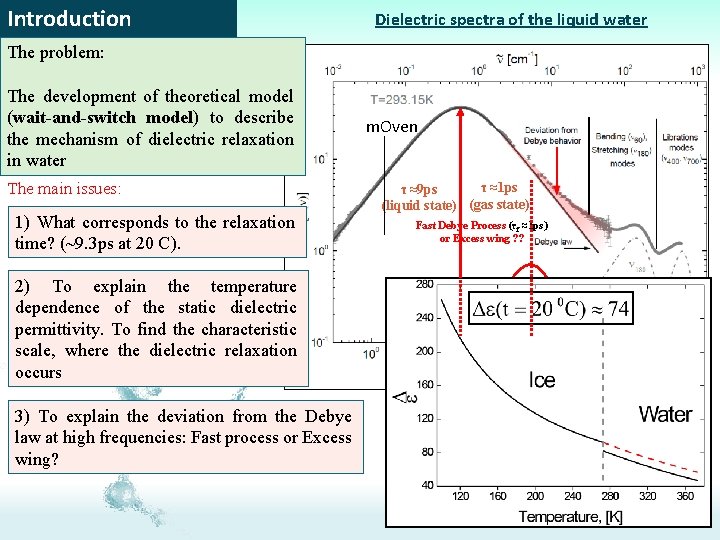
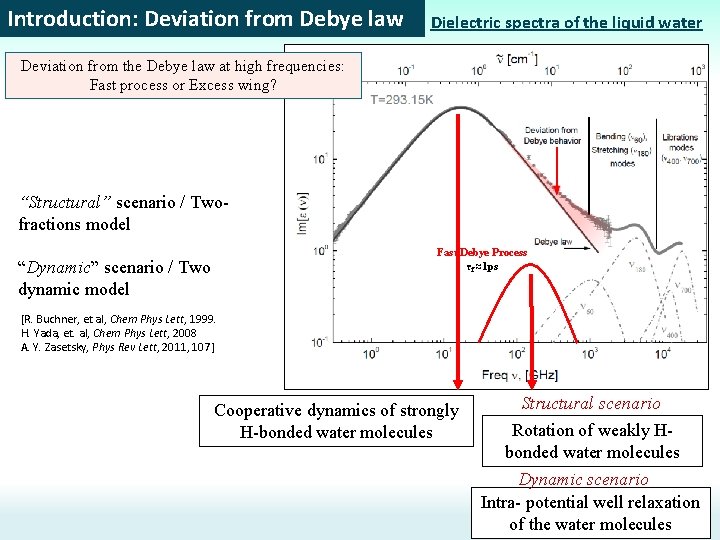
Introduction Dielectric spectra of the liquid water The problem: The development of theoretical model (wait-and-switch model) to describe the mechanism of dielectric relaxation in water The main issues: 1) What corresponds to the relaxation time? (~9. 3 ps at 20 C). 2) To explain the temperature dependence of the static dielectric permittivity. To find the characteristic scale, where the dielectric relaxation occurs 3) To explain the deviation from the Debye law at high frequencies: Fast process or Excess wing? m. Oven τ ≈1 ps τ ≈9 ps (liquid state) (gas state) Fast Debye Process (τf ≈1 ps) or Excess wing ? ?

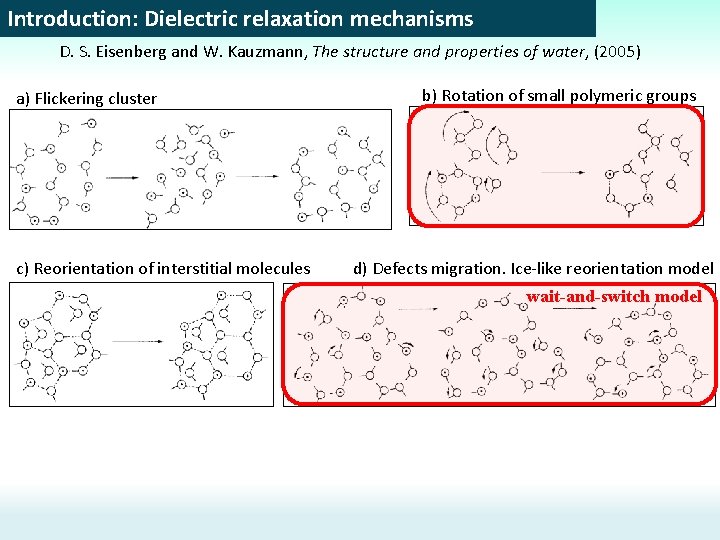
Introduction: Dielectric relaxation mechanisms D. S. Eisenberg and W. Kauzmann, The structure and properties of water, (2005) a) Flickering cluster c) Reorientation of interstitial molecules b) Rotation of small polymeric groups d) Defects migration. Ice-like reorientation model wait-and-switch model

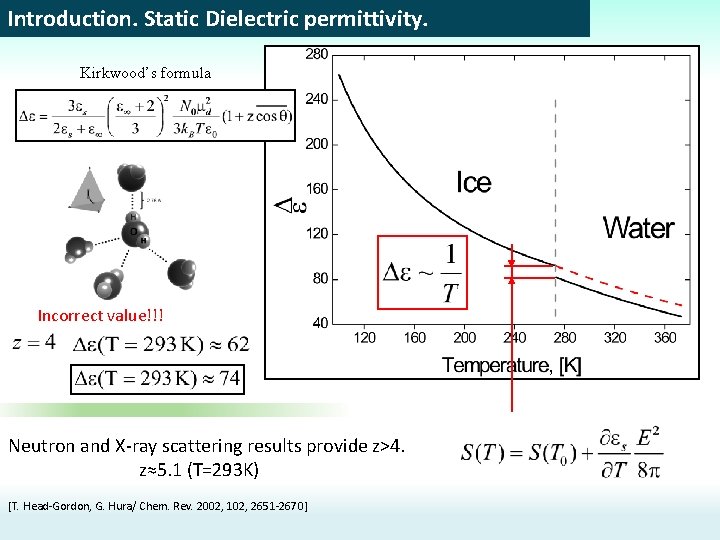
Introduction. Static Dielectric permittivity. Kirkwood’s formula Incorrect value!!! Neutron and X-ray scattering results provide z>4. z≈5. 1 (T=293 K) [T. Head-Gordon, G. Hura/ Chem. Rev. 2002, 102, 2651 -2670]

Introduction: Deviation from Debye law Dielectric spectra of the liquid water Deviation from the Debye law at high frequencies: Fast process or Excess wing? “Structural” scenario / Twofractions model Fast Debye Process τf ≈1 ps “Dynamic” scenario / Two dynamic model [R. Buchner, et al, Chem Phys Lett, 1999. H. Yada, et. al, Chem Phys Lett, 2008 A. Y. Zasetsky, Phys Rev Lett, 2011, 107] Cooperative dynamics of strongly H-bonded water molecules Structural scenario Rotation of weakly Hbonded water molecules Dynamic scenario Intra- potential well relaxation of the water molecules

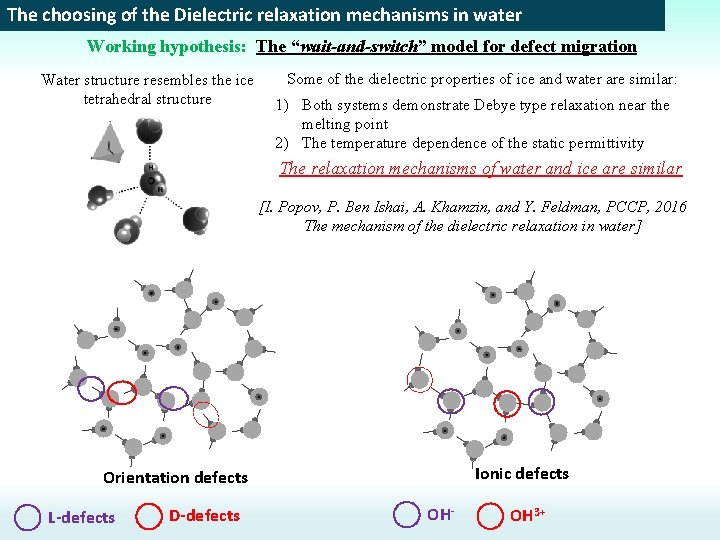
The choosing of the Dielectric relaxation mechanisms in water Working hypothesis: The “wait-and-switch” model for defect migration Water structure resembles the ice tetrahedral structure Some of the dielectric properties of ice and water are similar: 1) Both systems demonstrate Debye type relaxation near the melting point 2) The temperature dependence of the static permittivity The relaxation mechanisms of water and ice are similar [I. Popov, P. Ben Ishai, A. Khamzin, and Y. Feldman, PCCP, 2016 The mechanism of the dielectric relaxation in water] Ionic defects Orientation defects L-defects D-defects OH- OH 3+

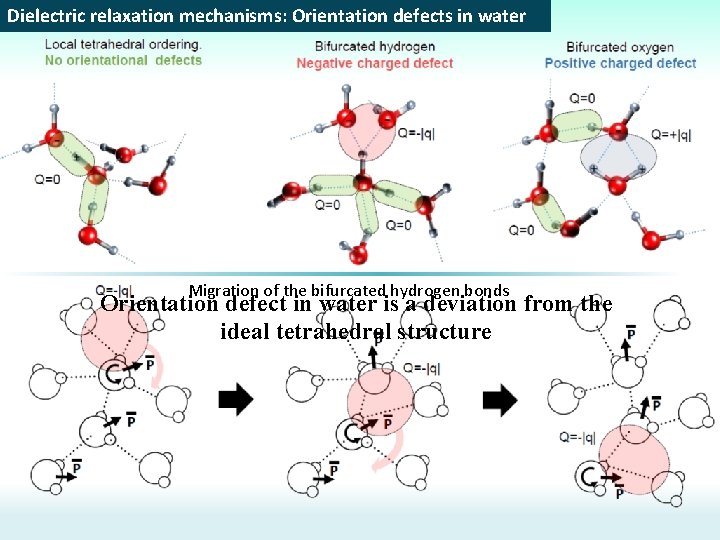
Dielectric relaxation mechanisms: Orientation defects in water Migration of the bifurcated hydrogen bonds Orientation defect in water is a deviation from the ideal tetrahedral structure

Relationship between complex dielectric permittivity and mean square displacement of the defects Rotation dynamic is coupled with diffusion of defects We can reduce the problem of water molecules rotation to the problem of random walk of defects!!! [I. Popov, P. Ben Ishai, A. Khamzin, and Y. Feldman, PCCP. , 2016, 18, 13941] N - is the number of defect types q- is a charge of the defect Experimental Results from other methods: Positive charged defect (D defect, Hydronium, bifurcated oxygen) Negative charged defect (L defect, Hydroxide, bifurcated proton) n – is a defect concentration 4) No reaction on p. H (time relaxation correlates with viscosity) Orientation defects are dominant.

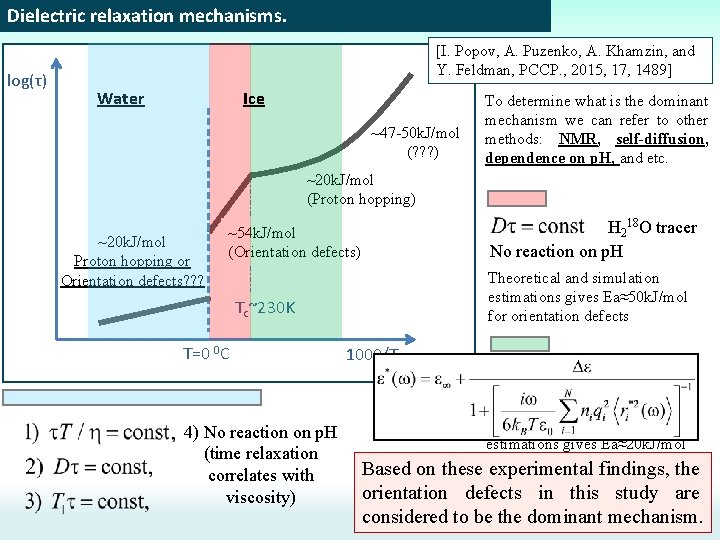
Dielectric relaxation mechanisms. log(τ) [I. Popov, A. Puzenko, A. Khamzin, and Y. Feldman, PCCP. , 2015, 17, 1489] Water Ice ~47 -50 k. J/mol (? ? ? ) To determine what is the dominant mechanism we can refer to other methods: NMR, self-diffusion, dependence on p. H, and etc. ~20 k. J/mol (Proton hopping) ~20 k. J/mol Proton hopping or Orientation defects? ? ? H 218 O tracer No reaction on p. H ~54 k. J/mol (Orientation defects) Theoretical and simulation estimations gives Ea≈50 k. J/mol for orientation defects Tc~230 K T=0 0 C 1000/T H 218 O tracer Reaction on p. H 4) No reaction on p. H (time relaxation correlates with viscosity) Theoretical and simulation estimations gives Ea≈20 k. J/mol proton hopping these for experimental findings, the Based on orientation defects in this study are considered to be the dominant mechanism.

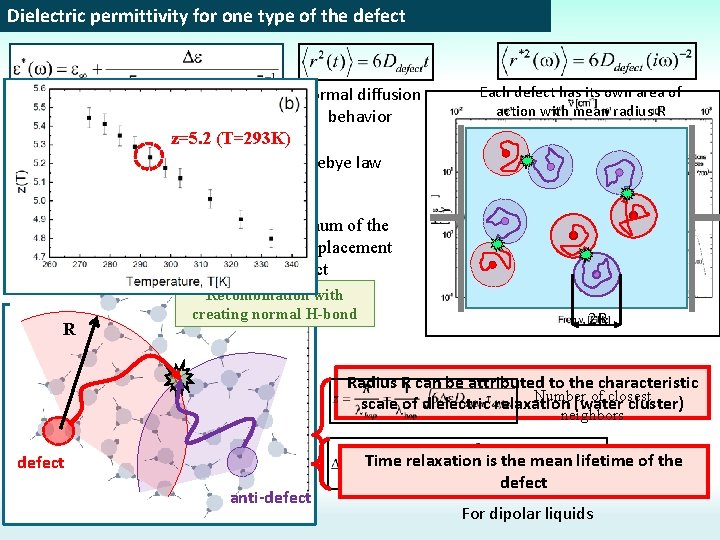
Dielectric permittivity for one type of the defect Normal diffusion behavior Each defect has its own area of action with mean radius R z=5. 2 (T=293 K) Debye law R- is the maximum of the mean square displacement of defect R Recombination with creating normal H-bond Equations systems Incorrect value!!! defect anti-defect 2 R Radius R can be attributed to the characteristic Number of closest scale of dielectric relaxation (water cluster) neighbors Kirkwood’s Time relaxation is the mean lifetime of the formula defect For dipolar liquids

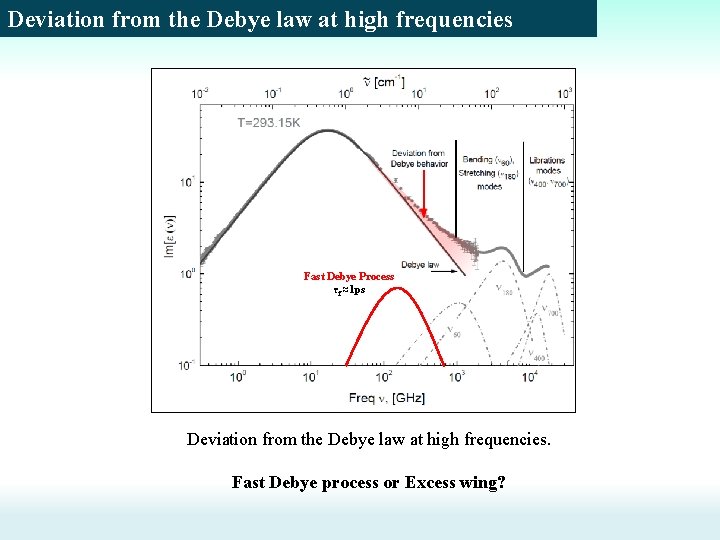
Deviation from the Debye law at high frequencies Fast Debye Process τf ≈1 ps Deviation from the Debye law at high frequencies. Fast Debye process or Excess wing?

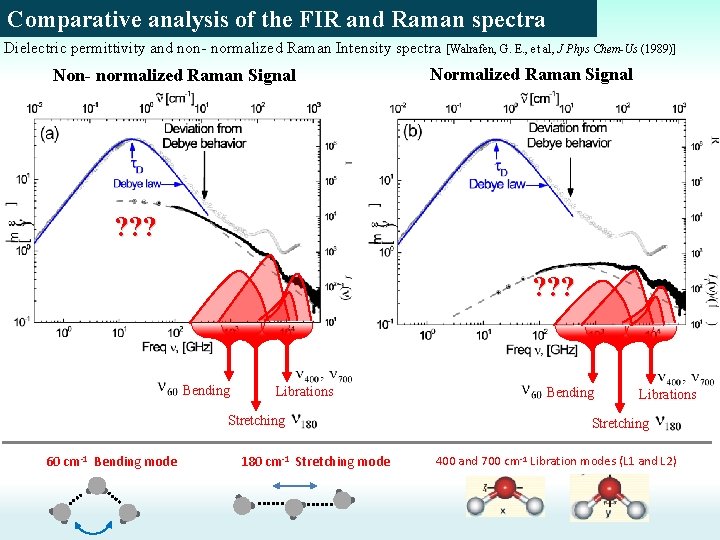
Comparative analysis of the FIR and Raman spectra Dielectric permittivity and non- normalized Raman Intensity spectra [Walrafen, G. E. , et al, J Phys Chem-Us (1989)] Non- normalized Raman Signal Normalized Raman Signal ? ? ? Bending Librations Stretching 60 cm-1 Bending mode 180 cm-1 Stretching mode Bending Librations Stretching 400 and 700 cm-1 Libration modes (L 1 and L 2)

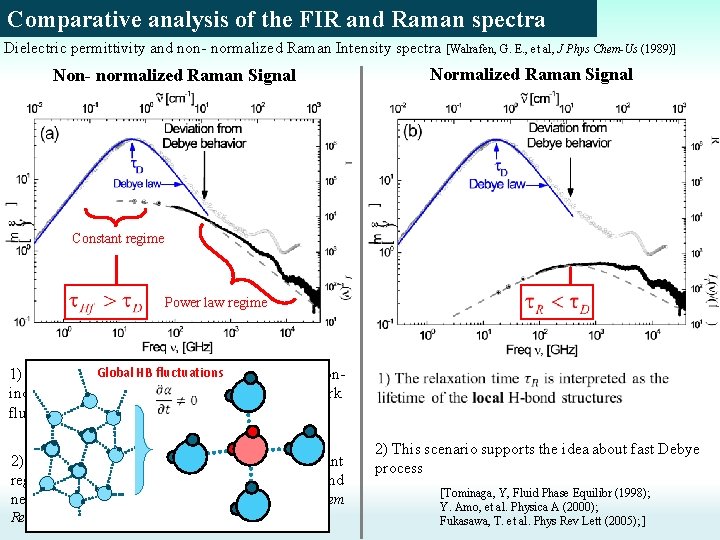
Comparative analysis of the FIR and Raman spectra Dielectric permittivity and non- normalized Raman Intensity spectra [Walrafen, G. E. , et al, J Phys Chem-Us (1989)] Non- normalized Raman Signal Normalized Raman Signal Constant regime Power law regime HB fluctuations 1) The Wide. Global background is related to collisioninduced processes due to global H-bond network fluctuations. [Walrafen, G. E. , et al, J Phys Chem-Us (1989)] 2) The crossover time from power law to constant regime is the relaxation time of the global H-bond network fluctuations ~20 -40 ps. [Ohmine, I. et al. Chem Rev (1993), Sasai, M. et al. J. Chem. Phys. (1992)] 2) This scenario supports the idea about fast Debye process [Tominaga, Y, Fluid Phase Equilibr (1998); Y. Amo, et al. Physica A (2000); Fukasawa, T. et al. Phys Rev Lett (2005); ]

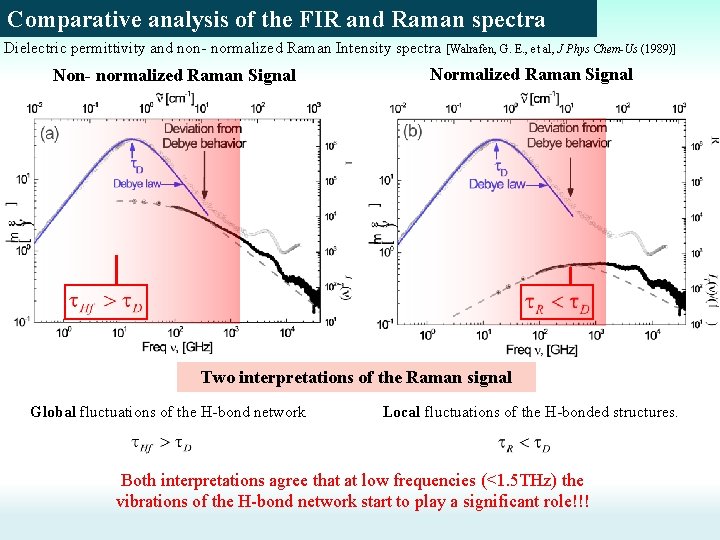
Comparative analysis of the FIR and Raman spectra Dielectric permittivity and non- normalized Raman Intensity spectra [Walrafen, G. E. , et al, J Phys Chem-Us (1989)] Non- normalized Raman Signal Normalized Raman Signal Two interpretations of the Raman signal Global fluctuations of the H-bond network Local fluctuations of the H-bonded structures. Both interpretations agree that at low frequencies (<1. 5 THz) the vibrations of the H-bond network start to play a significant role!!!

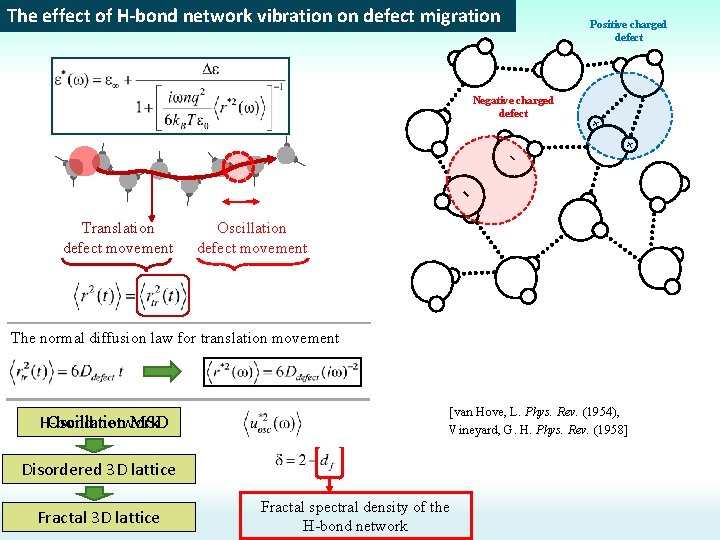
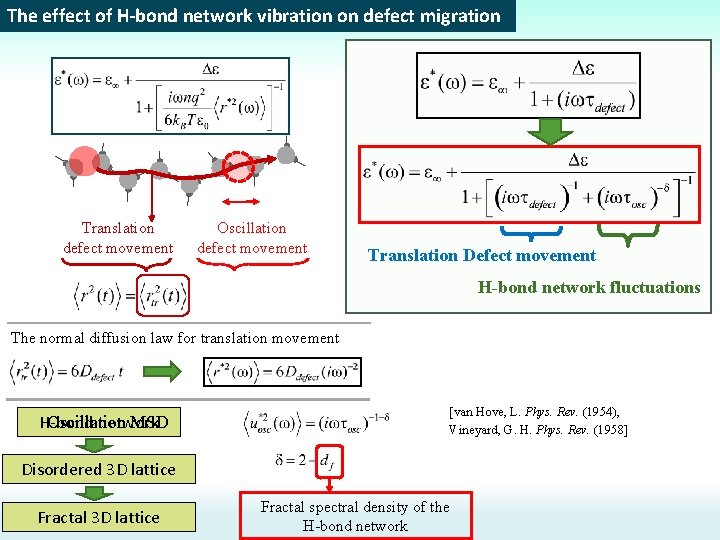
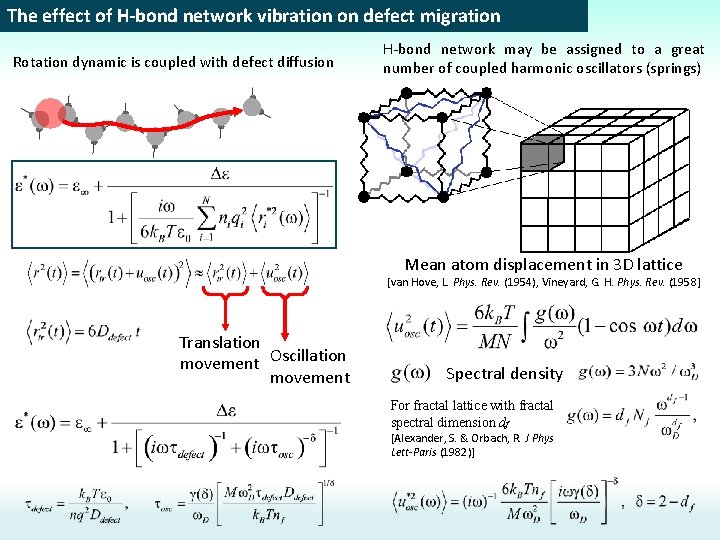
The effect of H-bond network vibration on defect migration Positive charged defect Negative charged defect + - + Translation defect movement Oscillation defect movement The normal diffusion law for translation movement H-bond network Oscillation MSD [van Hove, L. Phys. Rev. (1954), Vineyard, G. H. Phys. Rev. (1958] Disordered 3 D lattice Fractal spectral density of the H-bond network

The effect of H-bond network vibration on defect migration Translation defect movement Oscillation defect movement Translation Defect movement H-bond network fluctuations The normal diffusion law for translation movement H-bond network Oscillation MSD [van Hove, L. Phys. Rev. (1954), Vineyard, G. H. Phys. Rev. (1958] Disordered 3 D lattice Fractal spectral density of the H-bond network

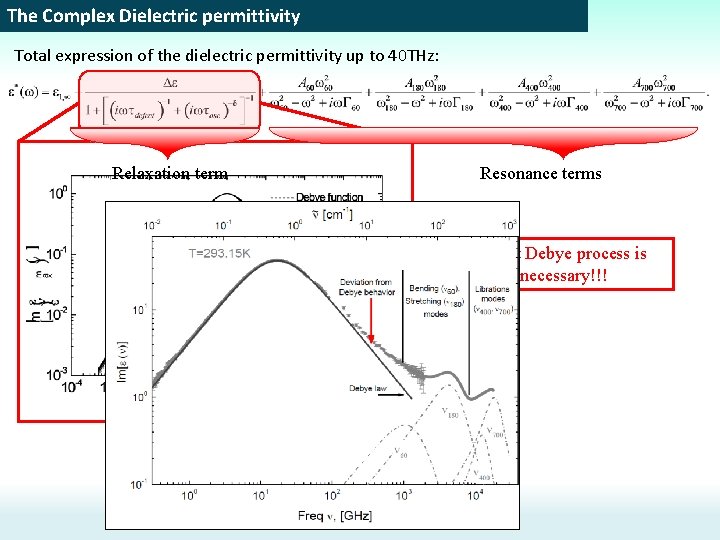
The Complex Dielectric permittivity Total expression of the dielectric permittivity up to 40 THz: Relaxation term Resonance terms The fast Debye process is unnecessary!!!

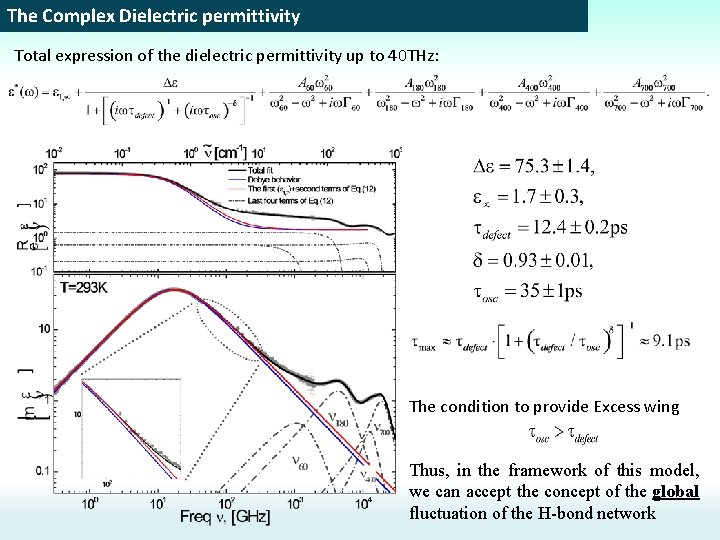
The Complex Dielectric permittivity Total expression of the dielectric permittivity up to 40 THz: The condition to provide Excess wing Thus, in the framework of this model, we can accept the concept of the global fluctuation of the H-bond network

The dielectric relaxation of ice Ih (Low temperature Crossover)

Dielectric relaxation mechanisms. Water log(τ) II I PCCP, 2016 PCCP, 2015 Ice III PCCP, 2017 ~47 -50 k. J/mol ~20 k. J/mol ~54 k. J/mol Tc~230 K ~20 k. J/mol T=0 0 C 1000/T

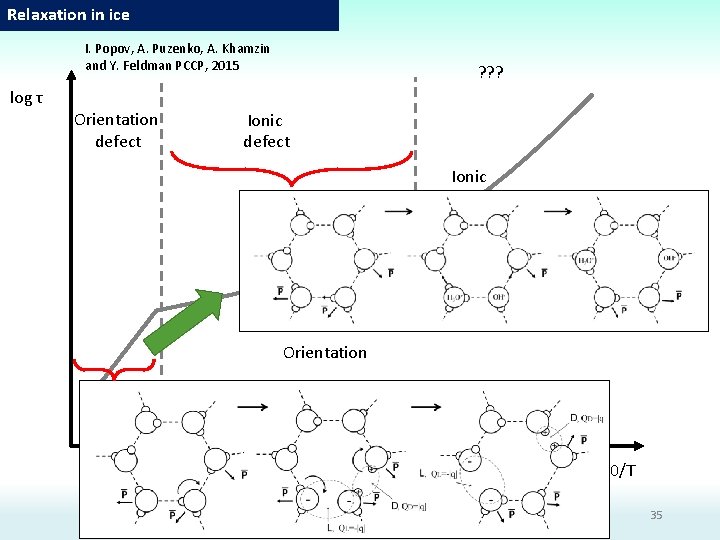
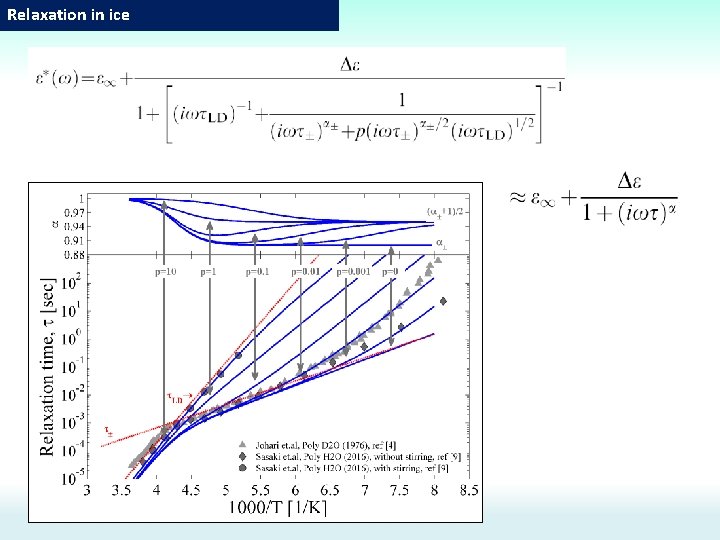
Relaxation in ice I. Popov, A. Puzenko, A. Khamzin and Y. Feldman PCCP, 2015 ? ? ? log τ Orientation defect Ionic Orientation 1000/T 35

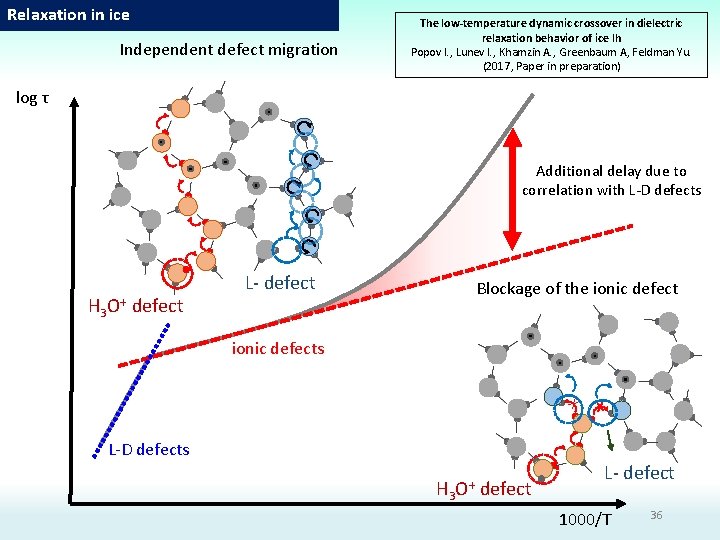
Relaxation in ice Independent defect migration The low-temperature dynamic crossover in dielectric relaxation behavior of ice Ih Popov I. , Lunev I. , Khamzin A. , Greenbaum A, Feldman Yu. (2017, Paper in preparation) log τ Additional delay due to correlation with L-D defects H 3 O+ defect L- defect Blockage of the ionic defects L-D defects H 3 O+ defect L- defect 1000/T 36

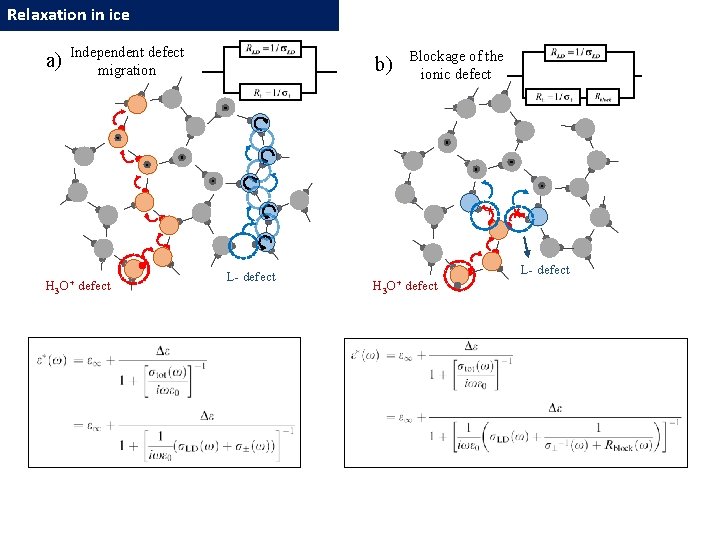
Relaxation in ice a) H 3 Independent defect migration O+ defect b) L- defect Blockage of the ionic defect L- defect H 3 O+ defect

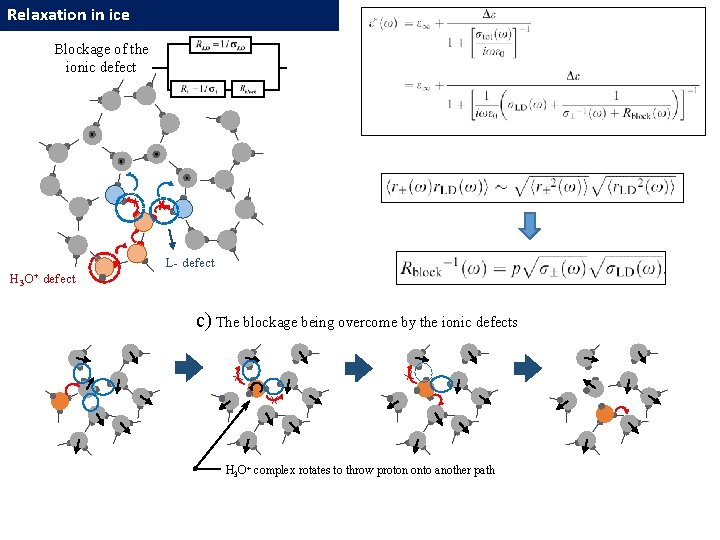
Relaxation in ice Blockage of the ionic defect L- defect H 3 O+ defect c) The blockage being overcome by the ionic defects H 3 O+ complex rotates to throw proton onto another path

Relaxation in ice

Relaxation in ice

Thank you for your attention !!!

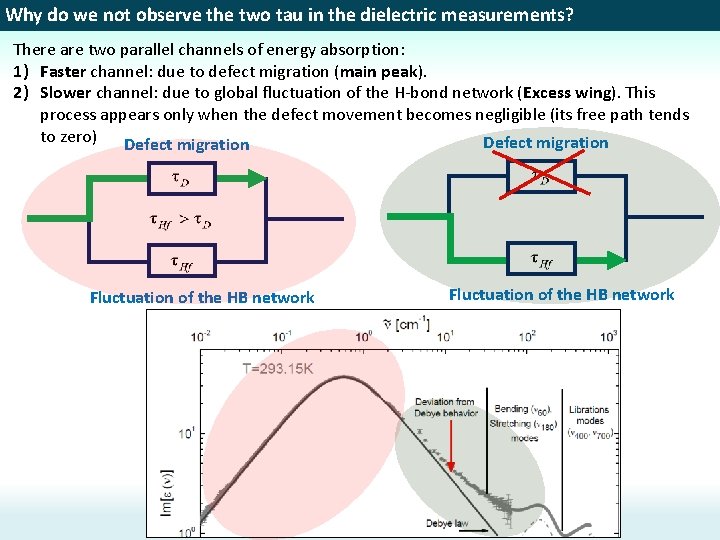
Why do we not observe the two tau in the dielectric measurements? There are two parallel channels of energy absorption: 1) Faster channel: due to defect migration (main peak). 2) Slower channel: due to global fluctuation of the H-bond network (Excess wing). This process appears only when the defect movement becomes negligible (its free path tends to zero) Defect migration Fluctuation of the HB network

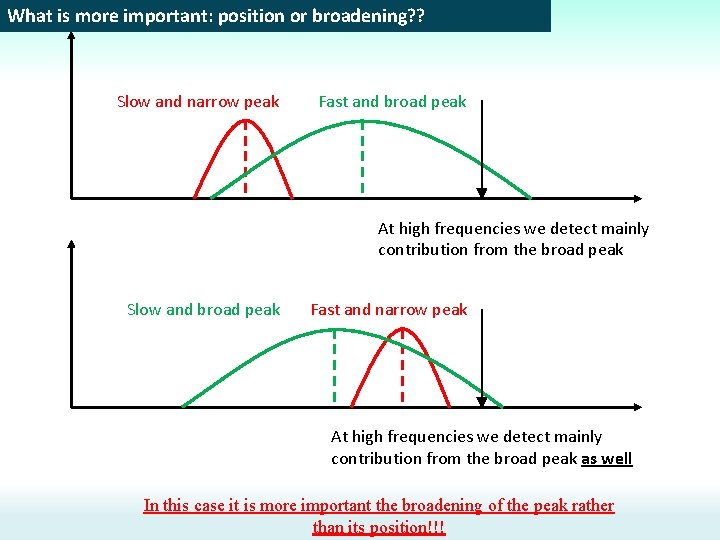
What is more important: position or broadening? ? Slow and narrow peak Fast and broad peak At high frequencies we detect mainly contribution from the broad peak Slow and broad peak Fast and narrow peak At high frequencies we detect mainly contribution from the broad peak as well In this case it is more important the broadening of the peak rather than its position!!!

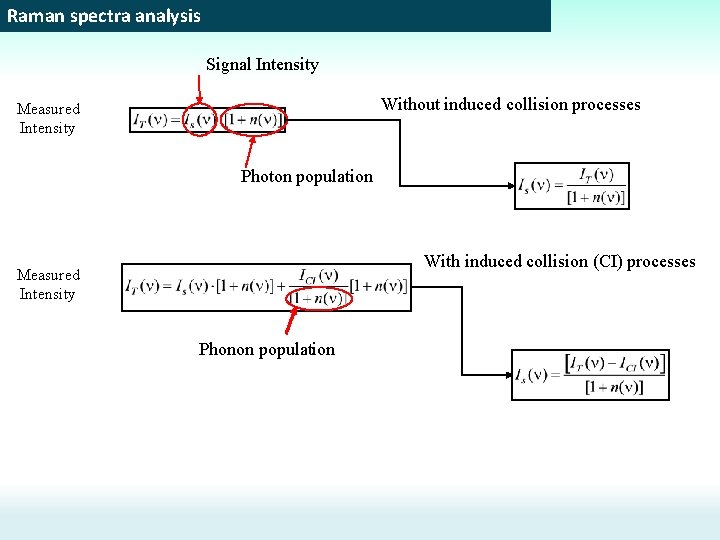
Raman spectra analysis Signal Intensity Without induced collision processes Measured Intensity Photon population With induced collision (CI) processes Measured Intensity Phonon population

The effect of H-bond network vibration on defect migration Rotation dynamic is coupled with defect diffusion H-bond network may be assigned to a great number of coupled harmonic oscillators (springs) Mean atom displacement in 3 D lattice [van Hove, L. Phys. Rev. (1954), Vineyard, G. H. Phys. Rev. (1958] Translation movement Oscillation movement Spectral density For fractal lattice with fractal spectral dimension df [Alexander, S. & Orbach, R. J Phys Lett-Paris (1982)]