The Mean of a Discrete Random Variable Lecture

The Mean of a Discrete Random Variable Lecture 23 Section 7. 5. 1 Wed, Oct 18, 2006

The Mean of a Discrete Random Variable n Mean of a Discrete Random Variable – The average of the values that the random variable takes on, in the long run.

The Mean of a Discrete Random Variable n The mean is also called the expected value. n If X is the number of sixes in a roll of two dice, then the mean of X is the expected number of sixes. However, that does not mean that it is the value that we literally expect to see. n “Expected value” is simply a synonym for the mean or average. n

The Mean of a Discrete Random Variable The mean, or expected value, of X may be denoted by either of two symbols. µX or E(X) n Usually there are no other variables to be confused with X, so we may write µ rather than µX. n

Example of the Mean How would we find the mean of the following pdf? n Why would it be wrong simply to average the numbers 1, 2, 3, and 4? n x 0 1 2 P(x) 0. 10 0. 30 0. 40 3 0. 20

Computing the Mean n Given the pdf of X, the mean is computed as n This is a weighted average of X. n Each value is weighted by its likelihood.

Example of the Mean n Recall the example where X was the number of children in a household. x 0 1 2 3 P (x ) 0. 10 0. 30 0. 40 0. 20

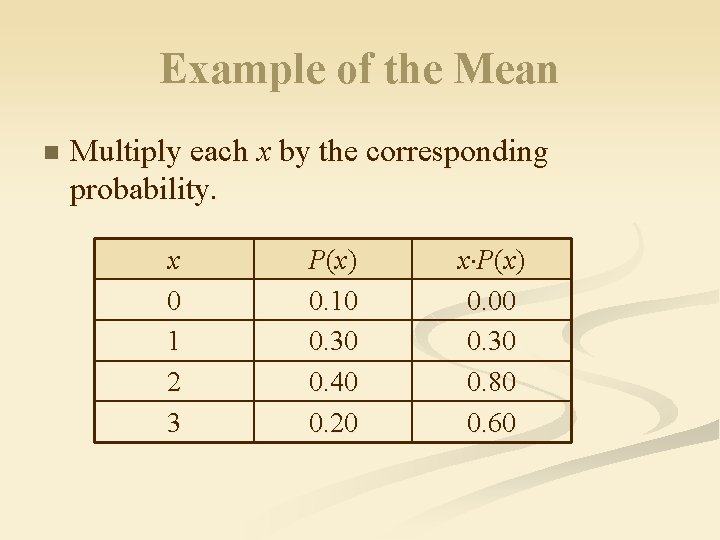
Example of the Mean n Multiply each x by the corresponding probability. x 0 1 2 3 P (x ) 0. 10 0. 30 0. 40 0. 20 x P(x) 0. 00 0. 30 0. 80 0. 60

Example of the Mean n Add up the column of products to get the mean. x 0 1 2 3 P (x ) 0. 10 0. 30 0. 40 0. 20 x P(x) 0. 00 0. 30 0. 80 0. 60 1. 70 = µ

Example: Powerball Use the handout to calculate the expected value of a Powerball ticket. n www. powerball. com n