The MaxCut problem Election recounts Majority vs Electoral

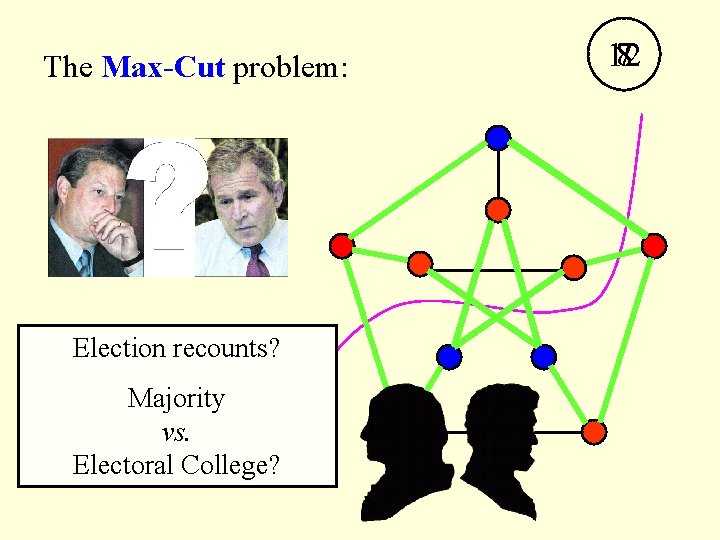
The Max-Cut problem: Election recounts? Majority vs. Electoral College? 12 78

The 2 -Lin(mod 3) problem: Simultaneously satisfy as many as you can.

2 -Variable Constraint Satisfaction Problems (“ 2 -CSPs”) Variables: x 1, x 2, x 3, … , xn Label Set: Input: Constraints 1, 2, …, N on pairs of variables. Output: Assignment satisfying as many constrs. as possible. (= allowed values for the variables) “Optimization”, “Approximation Algorithms”

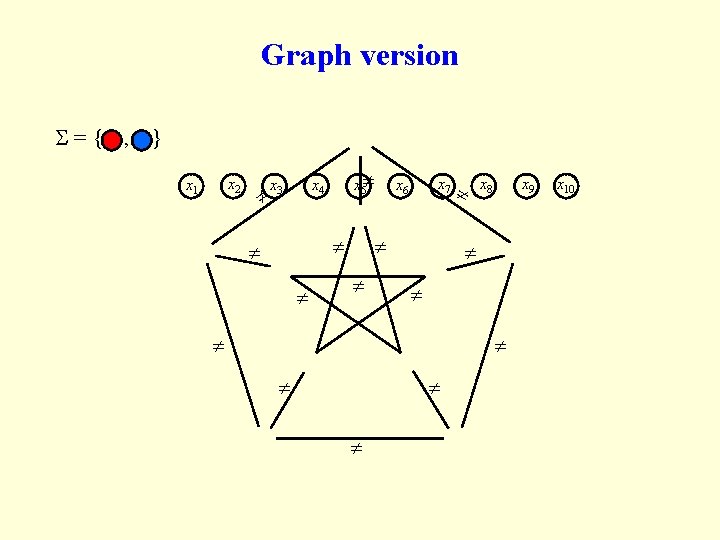
Graph version ={ , } x 2 x 1 x 3 x 5 x 4 x 7 x 6 x 9 x 8 x 10

2 -CSP examples Max-Cut: = {0, 1}, ’s of the form “ xi xj ” 2 -Lin(mod 3): (running example) = 3 , ’s of the form “xi = xj + c” 2 -SAT: = {0, 1}, ’s are , , , Vertex-Cover: Input: A graph. Goal: Select as few vertices as possible s. t. all edges are “covered”. Coloring 3 -colorable graphs: Input: a 3 -colorable graph. Goal: Legally color it using as few colors as possible.

Story of the talk 1. Egg on our face re complexity of algorithms for 2–CSPs. 2. Efficient “Property Testing” algs. ) Hardness for CSPs 3. Remarkably efficient (2–query!) Property Testing algs. exist.

Complexity theory dictum “Essentially every natural algorithmic problem has been shown to be in P (polynomial time) or NP-hard. ” (Exceptions: Factoring, Graph-Isomorphism. )

This is a lie. • Given a graph, find a cut achieving at least 90% of the max cut. • Given a 3 -colorable graph, color it using at most 100 colors. • Find a vertex cover at most 1. 99 times the minimum. • Find a 2 -SAT assignment satisfying 95% of the maximum. • Given (1− )-satisfiable 2 -Lin(mod p) system, satisfy (1/p) /2 fraction. • Find a cut within factor log log n of the sparsest cut. • (1 − 1/2 k)-approximate Max-k-Cut • …

We gotta do something about this! 1. Prove problems are in P. Seems we need a radically new algorithmic idea. Max-Cut: Most recent working algorithmic idea was from ’ 89–’ 92… Goemans-Williamson ’ 94 proved it always finds a cut achieving ¸ 87. 8567 % of the optimum. 2. Prove new NP-hardness results. Even after much effort, only some success. Not much for 2 -CSPs. (“PCP Theorem” [AS’ 92, ALMSS’ 92] + “Parallel Repetition Theorem” [Raz’ 95])

2 -CSPs? “Unique Games Conjecture” [Khot’ 02] [O’ 0? ] Max-3 -CSP [Khot’ 02] [ST’ 06] 2 -Lin(mod 2) Max-k-CSP [KR’ 03] Vertex-Cover [KKMO’ 04] [MOO’ 05] ( 87. 8567 % ) Max-Cut 2 -Lin(mod p) 2 -SAT [DMR’ 06] ([MOO’ 05]) Coloring 3 -Colorable Graphs A general theory is developing. [KO’ 06] Max-Cut-Gain [KV’ 05] Sparsest Cut

Story of the talk 1. Egg on our face re complexity of algorithms for 2–CSPs. 2. Efficient “Property Testing” algs. ) Hardness for CSPs 3. Remarkably efficient (2–query!) Property Testing algs. exist.

Property Testing = “Constant Time Algorithms” = “The art of uninformed decisions” Input: A “huge” object: e. g. , truth table f : m ! . Output: YES or NO, depending on whether it has property P. Caveat: You want to answer in constant time. What you can do: • Read f(x) for a few random x, say f(x 1 ), …, f(xk ). • Apply a “test”, ( f(x 1 ), …, f(xk ) ) ) YES / NO.

Testing “Dictatorships” For CSP hardness reductions, relevant P is being a “Dictatorship”: f(x) = xi f a Dictatorship ) test outputs YES with prob. ¸ p. YES f “very non-Dictatorial” ) test outputs YES with prob. · p. NO

Testing “Dictatorships” “ k-query, -based, (p. YES , p. NO) Dictatorship test ” (for an unknown f : m ! ) chosen at random (somehow) from m 1. x 1 , x 2, …, xk 2. ( f(x ), …, f(x ) ) 1 2 k is output, either YES or NO Requirement: f is a Dictatorship ) Pr[output YES] ¸ p. YES f “very non-Dictatorial” ) Pr[output YES] · p. NO

CSP hardness Rule of Thumb “ k-query, -based, (p. YES , p. NO) Dictatorship test ” NP-hardness (or “Unique Games Conjecture”) reduction for: p. NO “Satisfying a p fraction of the optimum, YES given a k-CSP instance with constraints. ” Remark: This idea is old: from [BGS’ 95]. Novelty: 2 -query Dictatorship tests exist!

Rule of Thumb example: Max-Cut: 2 -CSP over {0, 1} with constraints of form “ xi xj ”. 2 -query, “ ”-based, (90%, 80%) Dictator test for f : {0, 1}m ! {0, 1} ) “Assuming UGC, it is NP-hard to find cuts that achieve 88. 888 % of the optimal cut. ” 1. Pick x, y 2 {0, 1}m in some clever random way. 2. Query f(x), f(y) and output YES iff f(x) f(y). ) Dictatorships pass w. p. ¸ 90%, “Totally not Dictatorships” pass w. p. · 80%.

Story of the talk 1. Egg on our face re complexity of algorithms for 2–CSPs. 2. Efficient “Property Testing” algs. ) Hardness for CSPs 3. Remarkably efficient (2–query!) Property Testing algs. exist.

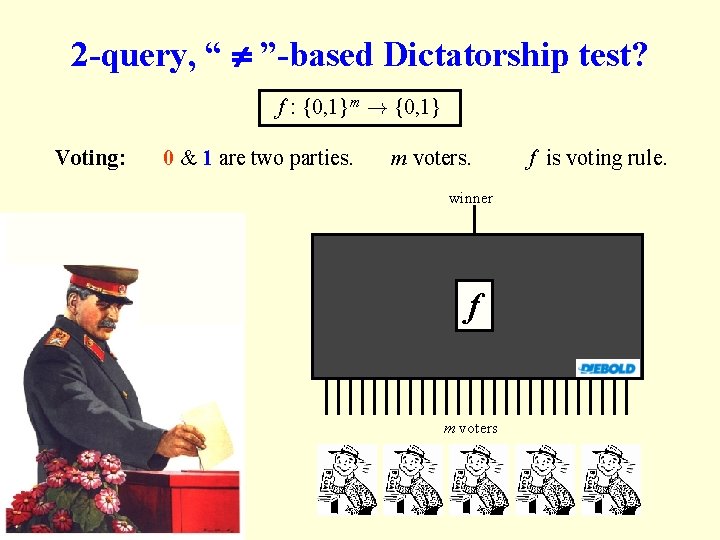
2 -query, “ ”-based Dictatorship test? f : {0, 1}m ! {0, 1} Voting: 0 & 1 are two parties. m voters. winner f m voters f is voting rule.

2 -query, “ ”-based Dictatorship test? [KKMO’ 04] suggestion: Election #1: Each voter flips a coin. Election #2: Each voter, with probability 90%, reverses their vote. Test: Winner #1 Winner #2. Prob[ Dictatorship passes ]: Prob[ Majority passes ]: 90% ¼ 79. 5% Prob[ Electoral College passes ]: ¼ 70. 1%

Majority Is The Highest [KKMO’ 04] conjectured, [MOO’ 05] proved: “Majority is the non-Dictator passing the test with highest probability. ” Hence: “ ”-based, ( 90% , 79. 5 % ) Hence: UGC-hardness of finding cut within Consequences: ) Dictatorship test. 79. 5% 90% ¼ 88. 4 % of Max Cut. ● [GW’ 94] is optimal Max Cut alg. , assuming UGC ● Resolves conjectures [Kalai’ 03, ’ 04] in theory of voting, also problems [ADFS ’ 04] in combinatorics. ● Result can be used to prove (sometimes improve) essentially all known UGC reductions.

2 -CSPs? “Unique Games Conjecture” [Khot’ 02] [O’ 0? ] Max-3 -CSP [Khot’ 02] [ST’ 06] 2 -Lin(mod 2) Max-k-CSP [KR’ 03] Vertex-Cover [KKMO’ 04] [MOO’ 05] ( 87. 8567 % ) Max-Cut 2 -Lin(mod p) 2 -SAT [DMR’ 06] ([MOO’ 05]) Coloring 3 -Colorable Graphs A general theory is developing. [KO’ 06] Max-Cut-Gain [KV’ 05] Sparsest Cut [MOO’ 05]

The proof that Majority is the highest 1. Generalize Central Limit Theorem. “Sums of random 0’s and 1’s ! Gaussians. ” “Polynomials of random 0’s and 1’s ! polynomials of Gaussians. ” 2. m Gaussians is like uniform distribution on m-dim. sphere. Problem becomes a cut problem on the sphere. Specifically “Min-Bisection”. 3. For small noise params (angles), essentially similar to finding the blob of half-volume w/ smallest perimeter. (Connections to Double Bubble problem. )

Open problems I’m thinking about 1. Prove Unique Games Conjecture. ([FKO]: trying to give reduction from Max-Cut hardness. ) 2. Analyze various other constant-query Dictatorship tests. 3. Change from the “Dictatorship test f : {0, 1}m ! {0, 1}” paradigm. ([KO’ 06] has some partial work on this. )