The Mathematics of Finance Chapter 6 The Mathematics

The Mathematics of Finance Chapter 6

The Mathematics of Finance Two principal concepts: � Present value � Future value Future Value and Present Value calculations, for our purpose, are inverse mathematical operations.

The Mathematics of Finance � Future Value (FV) is an amount as the result of a planned set of deposits (with interest), where the period interest rate (effective rate) is constant. The amount in an account is measured at some future time. � Present Value (PV) – is an amount that must be deposited/invested today (or equivalently, the purchase price of a Financial Asset) to make a planed set of withdrawals, such that the account balance (with interest) goes to zero immediately after the last withdrawal. The interest rate is the “effective” rate (per period). We presume it to be constant. � The “effective” rate - the rate of growth of wealth as the result of interest period

Calculations in the Mathematics of Finance 1) FV is $C (once) invested for one period, where r is the effective rate period. FV = C + r * C = C (1 + r) 2) PV of $C (once) after one period where r is the effective rate period. (How much you have to put in your account to receive $C at the end) PV = C / (1 + r)

Calculations in the Mathematics of Finance 3) FV of $C (once) after n periods, if r is the effective rate period FV = C (1 + r)n Rule of “ 7 “: If you invest at 10% it will take ~ 7 years to double your money. 4) PV of $C (once) after n periods if r is the effective rate period PV = C / (1 + r)n

Instances where it is easy to calculate the IRR a) IRR for one period investment (once)

Instances where it is easy to calculate the IRR b) IRR period for an investment that pays $C after n periods (once)

Calculations in the Mathematics of Finance An annuity is a set of n equal payments of $C each, one period, where r is the effective rate period. 5) FV of an annuity Case 1: FV of an annuity where your account balance is measured right after last deposit

Calculations in the Mathematics of Finance Case 2: FV of an annuity where your account balance is measured 1 period after last deposit Case 3: measure your account k ≥ 0 periods after the last deposit k = 0: Case 1 k = 1: Case 2

Calculations in the Mathematics of Finance 6) PV of an annuity Case 1: 1 st payment is in one period - Ordinary Annuity Case 2: 1 st payment is received immediately – Annuity Due

Calculations in the Mathematics of Finance 7) PV of accelerated or deferred annuity (relative to ordinary) k = 1: Ordinary annuity (Case 1) k = 0: Annuity-due (Case 2) k > 1 – differed relative to ordinary 0 < k < 1 – accelerated relative to ordinary

Calculations in the Mathematics of Finance Perpetuity is an indefinite into the future set of period payments of $C each. 8) PV of perpetuity Case 1: PV of Ordinary Perpetuity Case 2: PV of Perpetuity Due

Instances where it is easy to calculate the IRR c) IRR for an Ordinary Perpetuity d) IRR for a Perpetuity Due

Calculations in the Mathematics of Finance Growing Perpetuity: � C – 1 st payment � Each next payment is (1+g) greater than the previous 9) PV of a Growing Perpetuity g > 0 – growth g = 0 – no growth (regular perpetuity) g < 0 – declining perpetuity

Calculations in the Mathematics of Finance Case 1: PV of an Ordinary Growing Perpetuity Case 2: PV of a Perpetuity Due PV is finite number only if g < r g≠r

Instances where it is easy to calculate the IRR e) IRR for an Ordinary Growing Perpetuity f) IRR for a Growing Perpetuity Due

IRR – hypothetical discount rate that makes NPV = 0. General IRR:

Rates of Return The Holding-Period Rate of Return: PV – “Expenditure” on an investment FV – “Benefit”(or Wealth) of the investment at the end of the holding period including reinvested intermediate payments

Nominal & Effective Rates of Interest The effective rate of interest is the rate at which an investment account grows over the holding period In all PV and FV calculations we always use the effective rate The nominal rate of interest represents the way in which interest is calculated and added to investment account Also known as: ü Quoted rate ü Contract rate ü APR (Annual Percentage Rate) A nominal rate of interest is always accompanied by a compounding period.

Effective Rates of Interest a) Effective to effective (short to long) If r is the effective rate for a sub-period (short), then effective rate for a holding period composed of n subperiods (long) is: � geometric multiplication � power > 1

Nominal & Effective Rates of Interest b) Effective to effective (long to short) If r is the effective rate for a holding period composed of n sub-periods is: � geometric division � power < 1

Nominal & Effective Rates of Interest c) If i is the per annum rate compounded m times per year, then, the effective rate for one compound period is: also d) If i is the per annum rate compounded m times per year, then, the effective rate for n compound periods is:

Nominal & Effective Rates of Interest f) Continuous compounding (n = ∞) If i is the per annum rate compounded continuously, then, the effective annual rate (EAR) is:

Calculations in the Mathematics of Finance Growing Annuity 10) PV of a Growing Annuity 11) FV of a Growing Annuity

Calculations in the Mathematics of Finance Growing Annuity g=r PV of a Growing Annuity FV of a Growing Annuity

Calculations in the Mathematics of Finance Mortgage - is a mortgage loan secured by real property Is a French Law term meaning “death contract” Typical mortgage: � 25 years � Monthly payments Every payment has 2 parts: � Interest � Principal

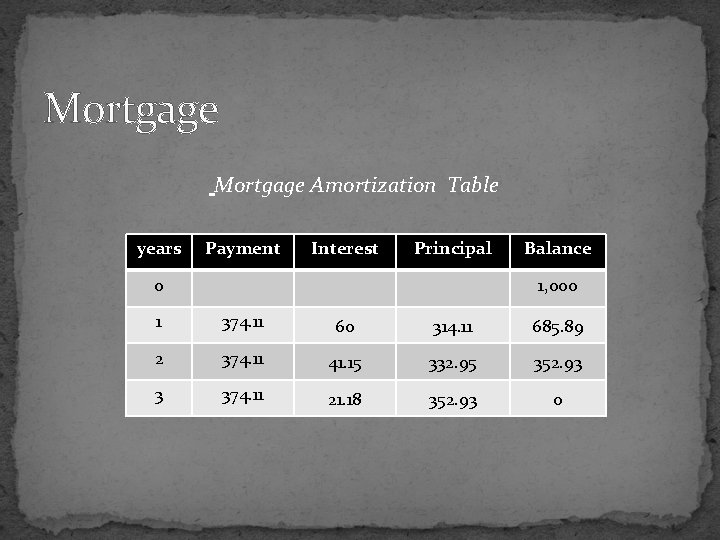
Mortgage Amortization Table years Payment Interest Principal 0 Balance 1, 000 1 374. 11 60 314. 11 685. 89 2 374. 11 41. 15 332. 95 352. 93 3 374. 11 21. 18 352. 93 0

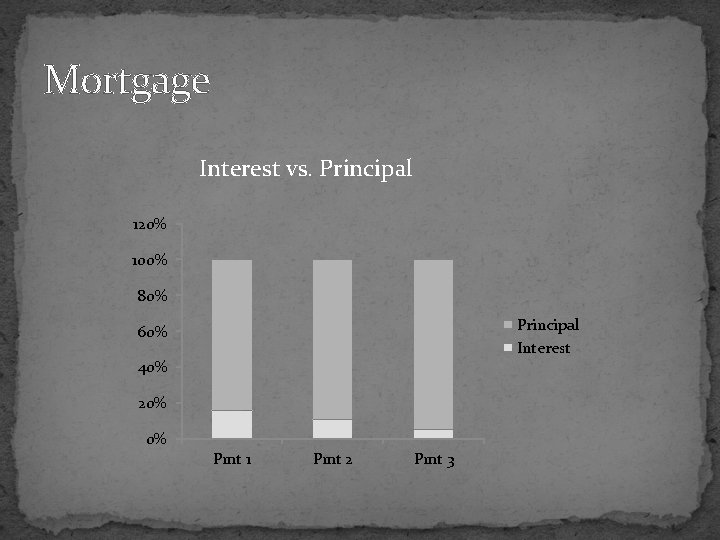
Mortgage Interest vs. Principal 120% 100% 80% Principal Interest 60% 40% 20% 0% Pmt 1 Pmt 2 Pmt 3

Mortgage Principal Repayment If a mortgage makes n payments and the mortgage rate is i% / annum compounded ( and paid) m times per year , then the principal repayment at the jth payment is:

Mortgage Canadian Mortgage Market: � Rates are stated APR compounded semi-annually � Rate of interest is periodically reset to market rate � Term – length of time over which the rate is fixed � Interest on mortgage payments (on your home) is not tax deductible Typical Canadian Mortgage : 25 years – Amortization period � 5 years term �