THE MATHEMATICAL MODELING AND COMPUTER ANALYSIS OF GENE

THE MATHEMATICAL MODELING AND COMPUTER ANALYSIS OF GENE NETWORKS

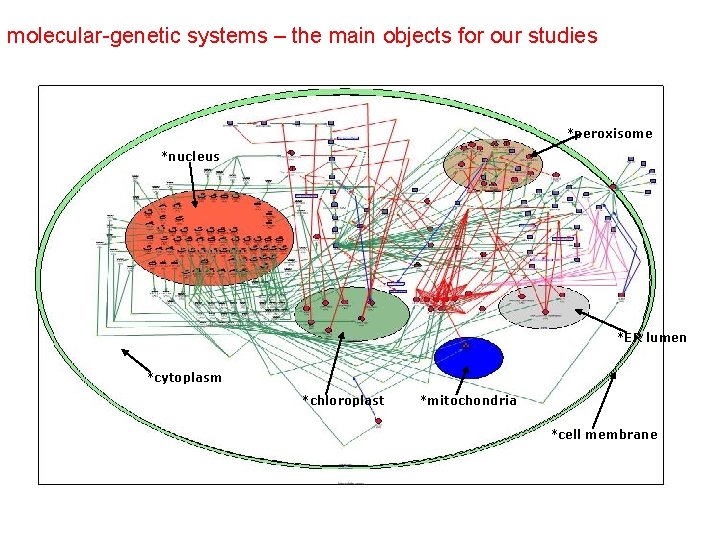
molecular-genetic systems – the main objects for our studies *peroxisome *nucleus *ER lumen *cytoplasm *chloroplast *mitochondria *cell membrane

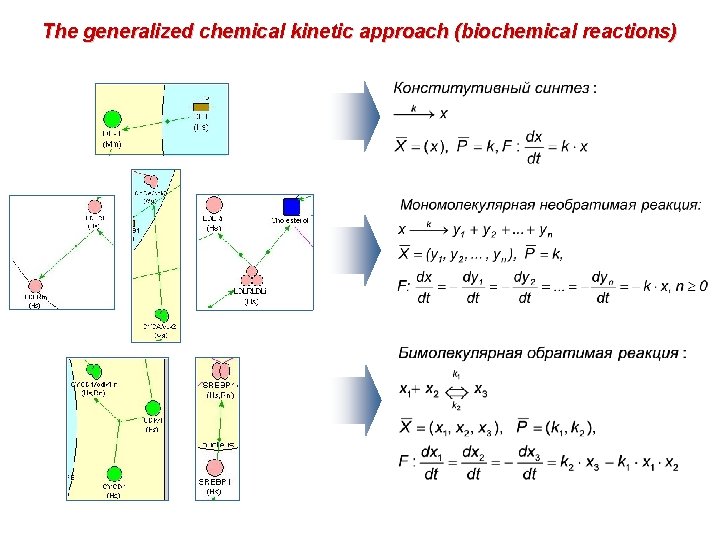
The generalized chemical kinetic approach (biochemical reactions)

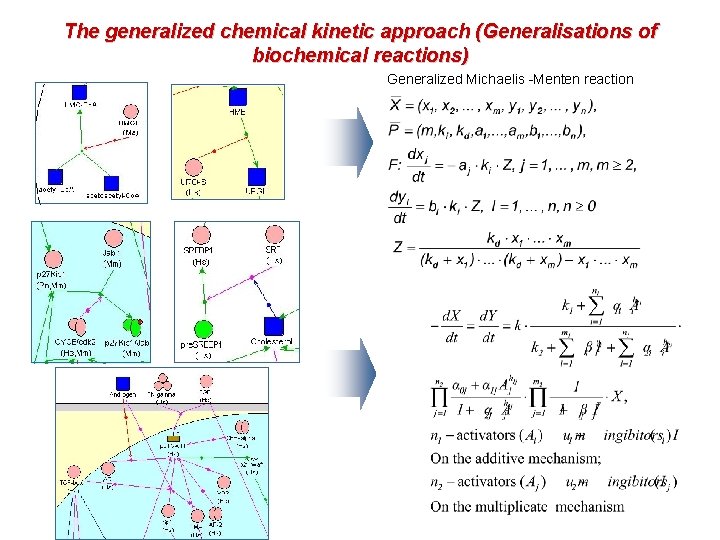
The generalized chemical kinetic approach (Generalisations of biochemical reactions) Generalized Michaelis -Menten reaction

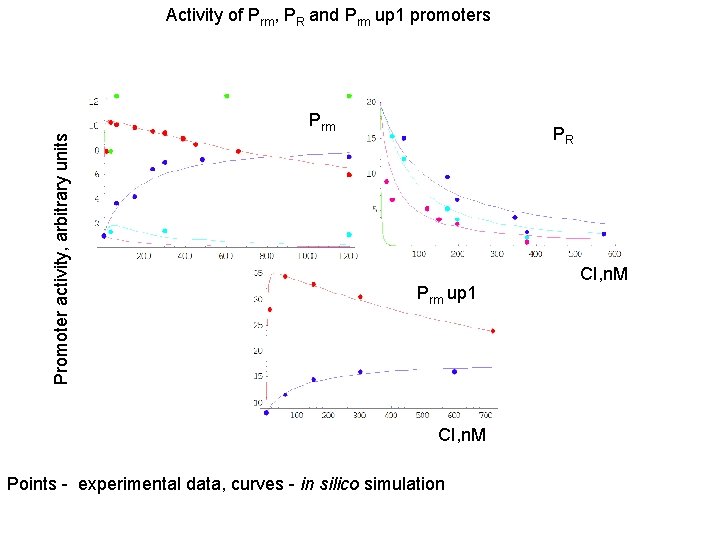
Prm-PR locus of lambda bacteriophage Prm up 1 mutation Biochemical model of Prm-PR locus activity regulation by TF CI and Cro

Promoter activity, arbitrary units Activity of Prm, PR and Prm up 1 promoters Prm PR Prm up 1 CI, n. M Points - experimental data, curves - in silico simulation CI, n. M

Generalised Hill Functions Generalized Hill Functions are the nonnegative rational polynoms with nonnegative parameters which also are Generalized Hill Functions. Subset GHF which is deduced from structural models of promoters and enzymatic reactions.

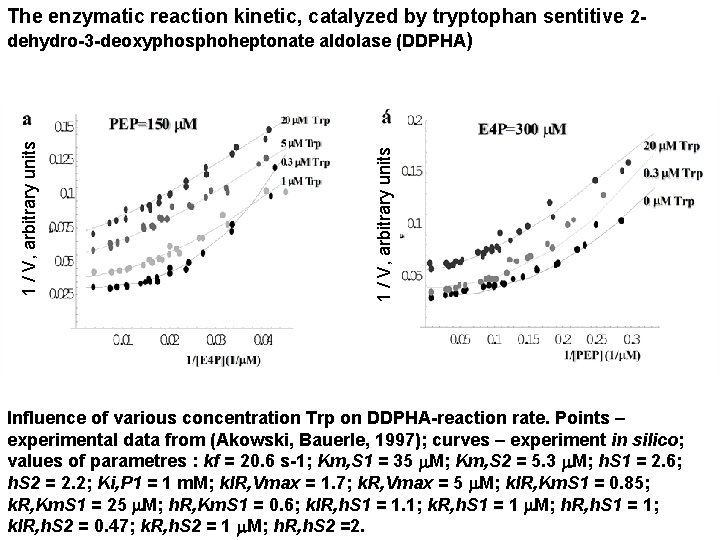
1 / V, arbitrary units The enzymatic reaction kinetic, catalyzed by tryptophan sentitive 2 dehydro-3 -deoxyphosphoheptonate aldolase (DDPHA) Influence of various concentration Trp on DDPHA-reaction rate. Points – experimental data from (Akowski, Bauerle, 1997); curves – experiment in silico; values of parametres : kf = 20. 6 s-1; Km, S 1 = 35 M; Km, S 2 = 5. 3 M; h. S 1 = 2. 6; h. S 2 = 2. 2; Ki, P 1 = 1 m. M; kl. R, Vmax = 1. 7; k. R, Vmax = 5 M; kl. R, Km. S 1 = 0. 85; k. R, Km. S 1 = 25 M; h. R, Km. S 1 = 0. 6; kl. R, h. S 1 = 1. 1; k. R, h. S 1 = 1 M; h. R, h. S 1 = 1; kl. R, h. S 2 = 0. 47; k. R, h. S 2 = 1 M; h. R, h. S 2 =2.

GHF model of DDPHA-reaction V - specific rate of reaction; S 1 - concentration of E 4 P, S 2 - concentration of PEP, P 1 - concentration of PI, P 2 - concentration of 3 DDAH 7 P, R - concentrations of Trp.

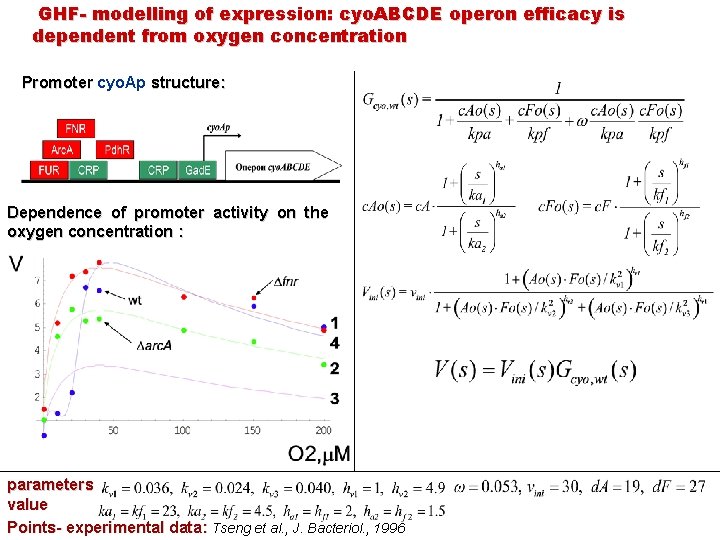
GHF- modelling of expression: cyо. ABCDE operon efficacy is dependent from oxygen concentration Promoter cyo. Ap structure: Dependence of promoter activity on the oxygen concentration : parameters value Points- experimental data: Tseng et al. , J. Bacteriol. , 1996

With application of a hierarchical method of modeling we have developed the following mathematical models: The phage lambda ontogenesis Artificial gene Networks The cholesterol homeostasis The Auxin synthesis and transport in a plant root and shoot The evolution of the elementary self-reproduced system The endocellular stage in development of an influenza virus Hepatitis virus C replicon replication The frog life water stage cycle in development Trematoda parasite life cycle And some others

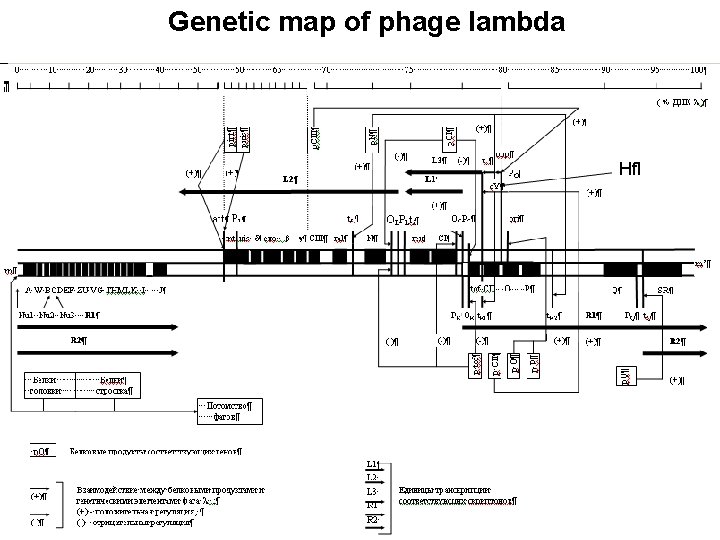
Genetic map of phage lambda Hfl

The Model of the phage lambda ontogenesis Phage lambda genetic elements described as elementary models 1. Promoters Pi, PL, Prm, PR, Pre, P R. 2. Transcription terminations ti, t. L 3, t. L 2, t. L 1, t. R 2, t Q 3. Protein-coding phage lambda genes 4. Antitermination sites NUTL, NUTR 5. Origin replication site ori 6. Spacers.

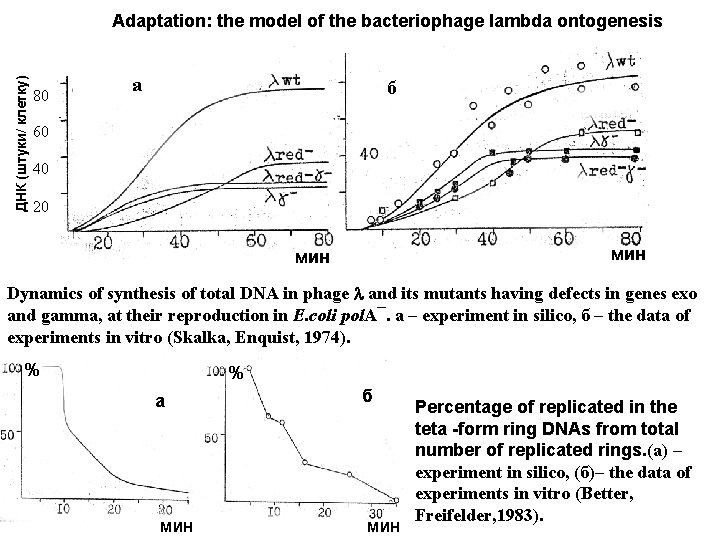
ДНК (штуки/ клетку) Adaptation: the model of the bacteriophage lambda ontogenesis 80 а б 60 40 20 мин Dynamics of synthesis of total DNA in phage and its mutants having defects in genes exo and gamma, at their reproduction in E. coli pol. A¯. a – experiment in silico, б – the data of experiments in vitro (Skalka, Enquist, 1974). % % a мин б мин Percentage of replicated in the teta -form ring DNAs from total number of replicated rings. (а) – experiment in silico, (б)– the data of experiments in vitro (Better, Freifelder, 1983).

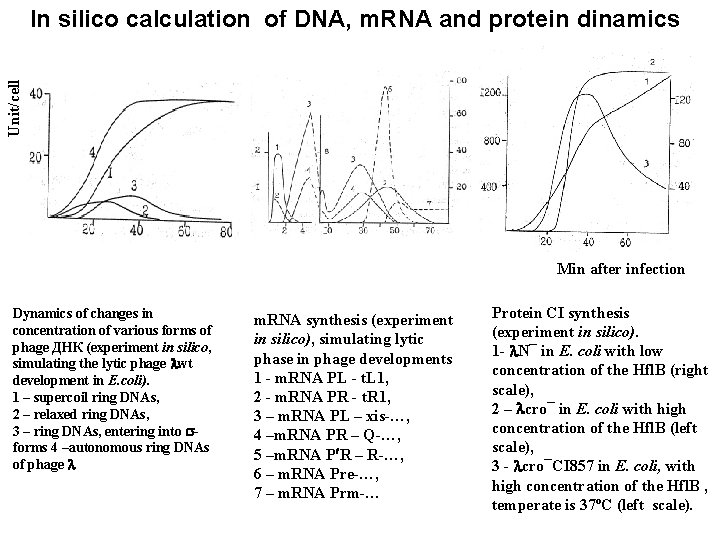
Unit/cell In silico calculation of DNA, m. RNA and protein dinamics Min after infection Dynamics of changes in concentration of various forms of phage ДНК (experiment in silico, simulating the lytic phage wt development in E. coli). 1 – supercoil ring DNAs, 2 – relaxed ring DNAs, 3 – ring DNAs, entering into forms 4 –autonomous ring DNAs of phage m. RNA synthesis (experiment in silico), simulating lytic phase in phage developments 1 - m. RNA PL - t. L 1, 2 - m. RNA PR - t. R 1, 3 – m. RNA PL – xis-…, 4 –m. RNA PR – Q-…, 5 –m. RNA P R – R-…, 6 – m. RNA Pre-…, 7 – m. RNA Prm-… Protein CI synthesis (experiment in silico). 1 - N¯ in E. сoli with low concentration of the Hfl. B (right scale), 2 – cro¯ in E. сoli with high concentration of the Hfl. B (left scale), 3 - cro¯CI 857 in E. сoli, with high concentration of the Hfl. B , temperate is 37ºС (left scale).

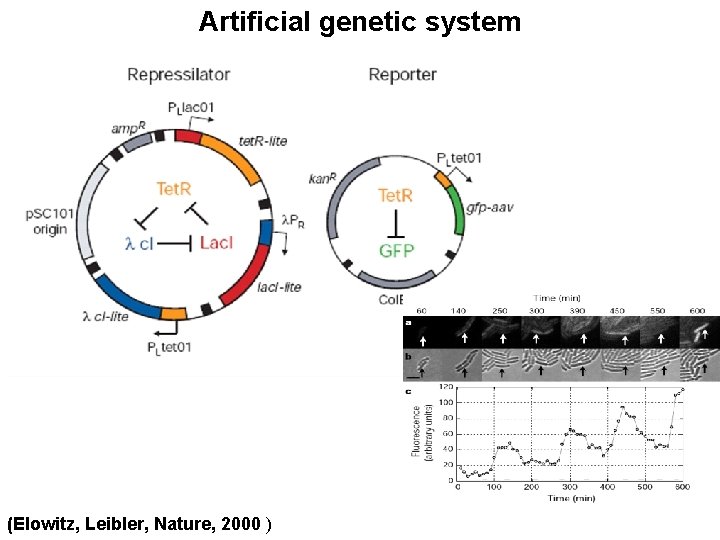
Artificial genetic system (Elowitz, Leibler, Nature, 2000 )

Simulation of Elowitz-Leibler repressilator Experiment in silico Experimental data [Elowitz, Leibler, 2000]

Gene Network theory

The hierarchical organisation of gene networks structure, as dynamic systems Structural level functional level parameter level HGN

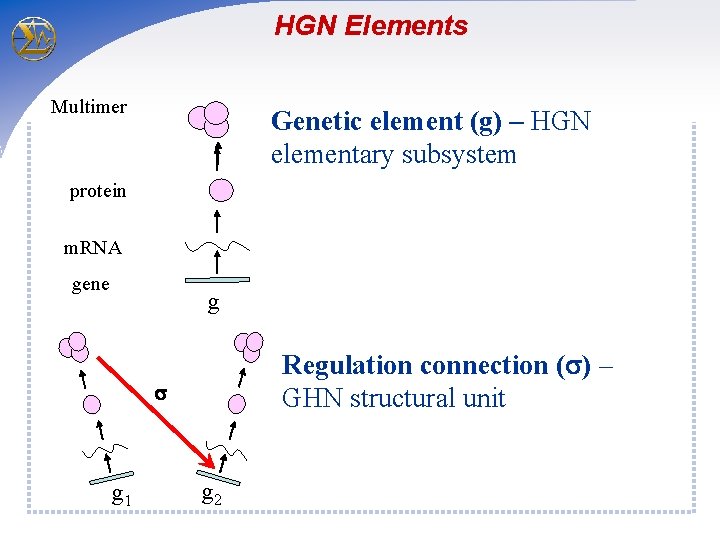
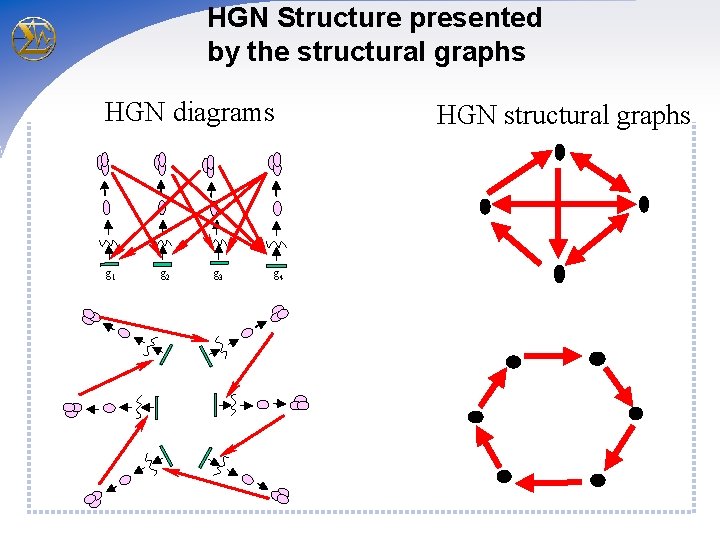
HGN Elements Multimer Genetic element (g) – HGN elementary subsystem protein m. RNA gene g Regulation connection ( ) – GHN structural unit g 1 g 2

HGN Structure presented by the structural graphs HGN diagrams g 1 g 2 g 3 g 4 HGN structural graphs

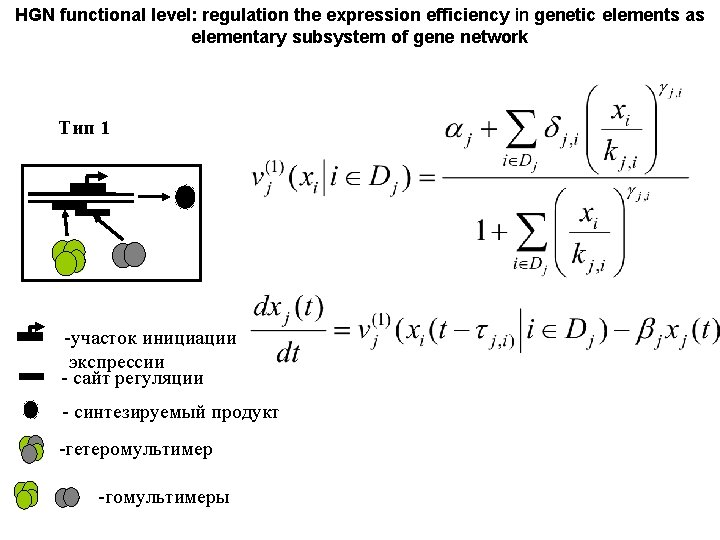
HGN functional level: regulation the expression efficiency in genetic elements as elementary subsystem of gene network Тип 1 -участок инициации экспрессии - сайт регуляции - синтезируемый продукт -гетеромультимер -гомультимеры

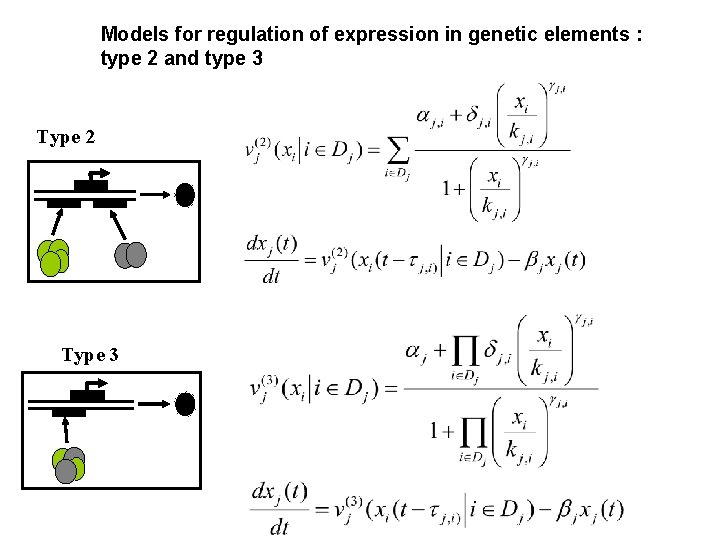
Models for regulation of expression in genetic elements : type 2 and type 3 Type 2 Type 3

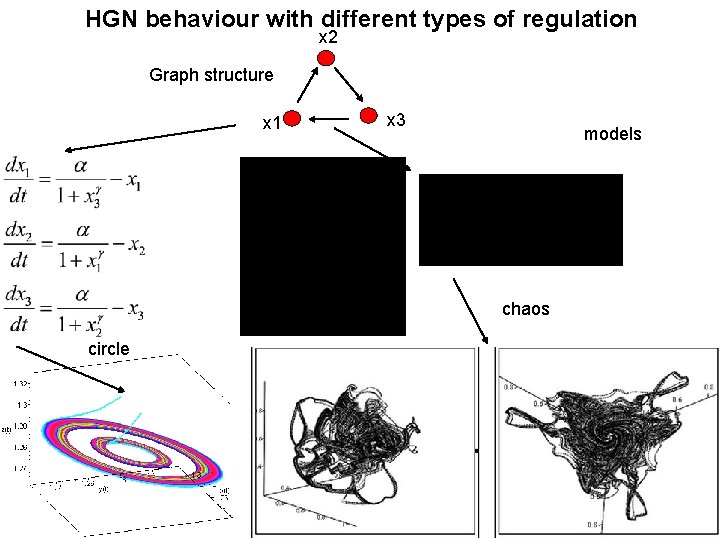
HGN behaviour with different types of regulation x 2 Graph structure x 1 x 3 models chaos circle

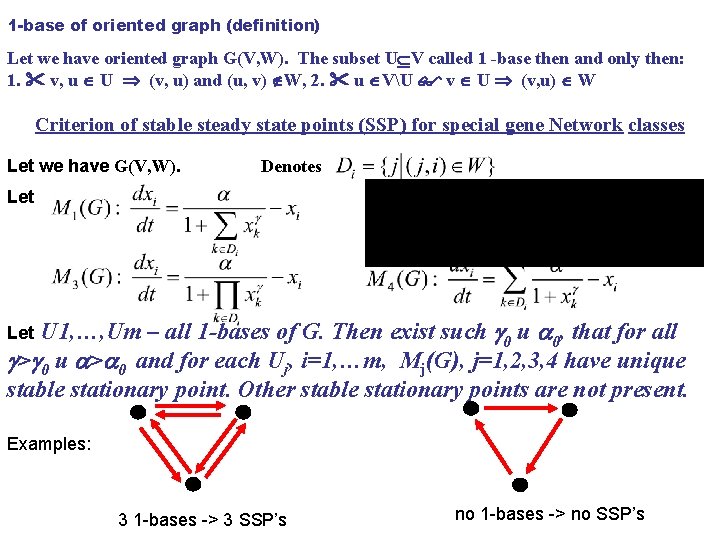
1 -base of oriented graph (definition) Let we have oriented graph G(V, W). The subset U V called 1 -base then and only then: 1. v, u U (v, u) and (u, v) W, 2. u VU v U (v, u) W Criterion of stable steady state points (SSP) for special gene Network classes Let we have G(V, W). Denotes Let U 1, …, Um – all 1 -bases of G. Then exist such 0 и 0, that for all > 0 и > 0 and for each Uj, i=1, …m, Mj(G), j=1, 2, 3, 4 have unique stable stationary point. Other stable stationary points are not present. Let Examples: 3 1 -bases -> 3 SSP’s no 1 -bases -> no SSP’s

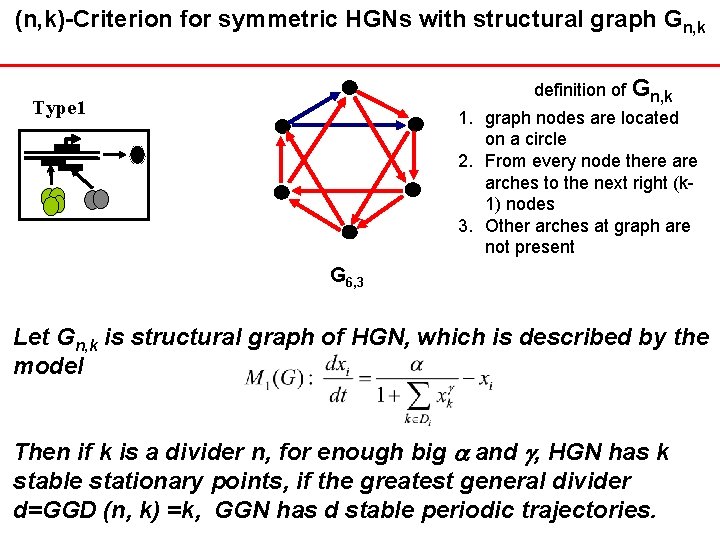
(n, k)-Criterion for symmetric HGNs with structural graph Gn, k definition of Gn, k Тype 1 1. graph nodes are located on a circle 2. From every node there arches to the next right (k 1) nodes 3. Other arches at graph are not present G 6, 3 Let Gn, k is structural graph of HGN, which is described by the model Then if k is a divider n, for enough big and , HGN has k stable stationary points, if the greatest general divider d=GGD (n, k) =k, GGN has d stable periodic trajectories.

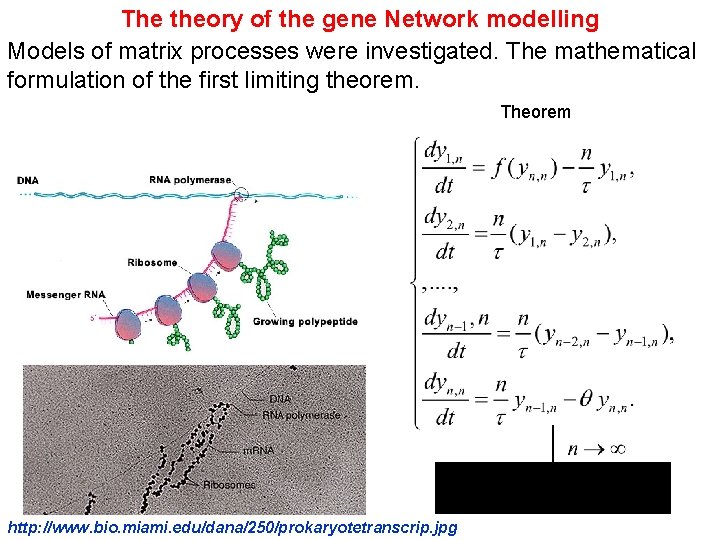
The theory of the gene Network modelling Models of matrix processes were investigated. The mathematical formulation of the first limiting theorem. Theorem http: //www. bio. miami. edu/dana/250/prokaryotetranscrip. jpg

THANKS FOR YOUR ATTENTION