The Math Behind the Compact Disc Linear Algebra

The Math Behind the Compact Disc Linear Algebra and Error-Correcting Codes william j. martin. mathematical sciences. wpi wednesday december 3. 2008 fairfield university

How the device works The compact disc is a complex system incorporating interesting ideas from engineering, physics, CS and math. We will focus only on the mathematics of the error- correction strategy. For more info on the CD, see Kelin Kuhn’s book “Laser Engineering”: 3/9/2021 W J Martin Mathematical Sciences WPI

Borrowed from K J Kuhn’s book “Laser Engineering” 3/9/2021 W J Martin Mathematical Sciences WPI

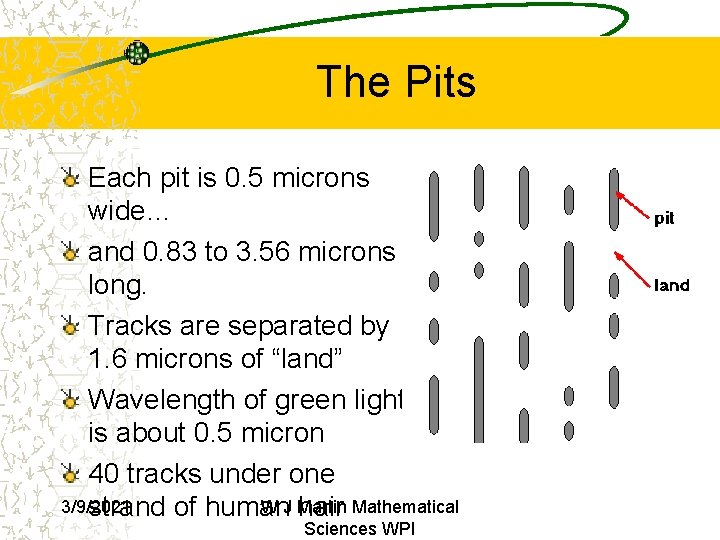
The Pits Each pit is 0. 5 microns wide… and 0. 83 to 3. 56 microns long. Tracks are separated by 1. 6 microns of “land” Wavelength of green light is about 0. 5 micron 40 tracks under one 3/9/2021 W J Martin strand of human hair Mathematical Sciences WPI

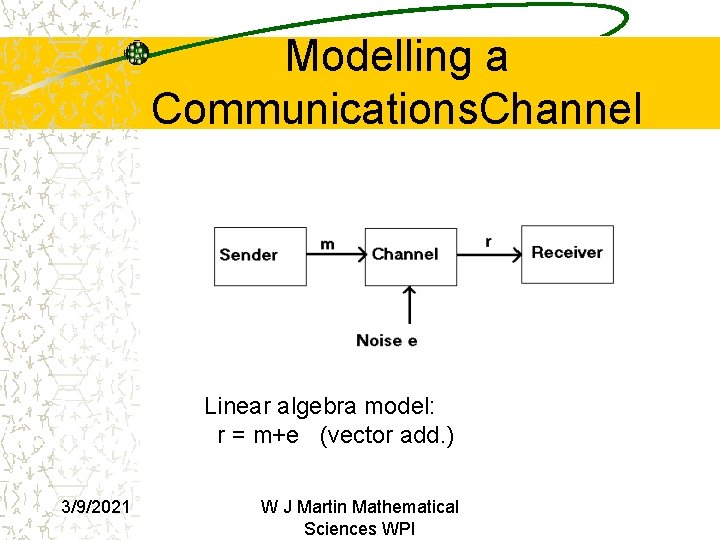
Modelling a Communications. Channel Linear algebra model: r = m+e (vector add. ) 3/9/2021 W J Martin Mathematical Sciences WPI

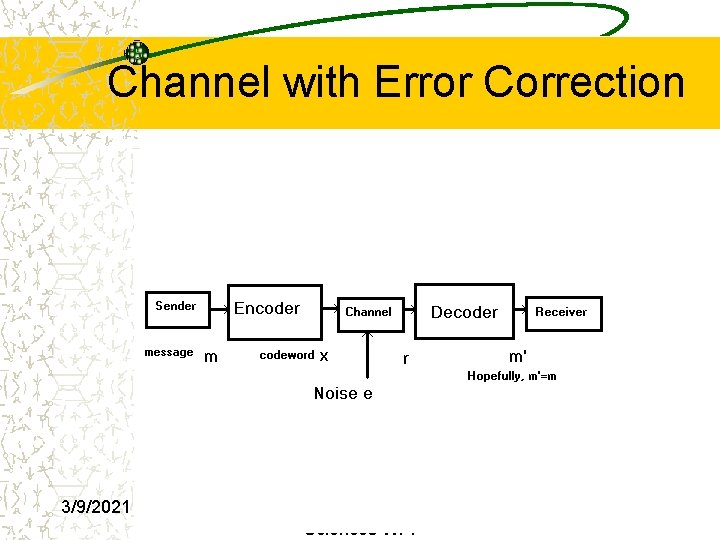
Channel with Error Correction 3/9/2021 W J Martin Mathematical Sciences WPI

Turn it into an algebra problem! A number system that the computer can understand: F = { 0, 1 } Ordinary multiplication Addition: 1+1=0 3/9/2021 Now music is turned into binary vectors! W J Martin Mathematical Sciences WPI

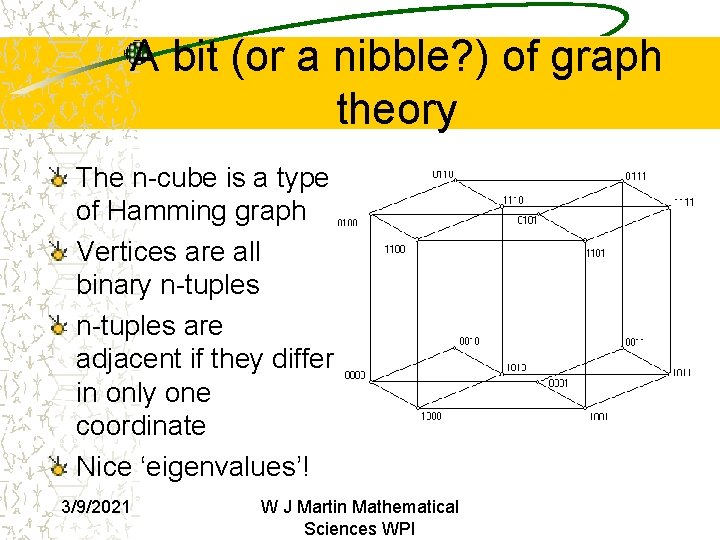
A bit (or a nibble? ) of graph theory The n-cube is a type of Hamming graph Vertices are all binary n-tuples are adjacent if they differ in only one coordinate Nice ‘eigenvalues’! 3/9/2021 W J Martin Mathematical Sciences WPI

Binary Vector Spaces The vectors are all possible binary ntuples 001011101011000 + 00111100001 = 000100101011001 3/9/2021 W J Martin Mathematical Sciences WPI

Hamming Distance The distance between two binary n-tuples x and y is the number of coordinates in which they differ dist( 001100, 001011 ) = 3 This is a metric: dist( x, y ) 0 with dist( x, y ) = 0 iff x=y dist( x, y ) = dist( y, x ) Triangle inequality dist( x, z ) dist( x, y ) + dist( y, z ) 3/9/2021 W J Martin Mathematical Sciences WPI

Theorem n Let C (the “code”) be a subset of F with minimum distance between any two codewords equal to d. Then there exists an algorithm which corrects up to t errors per transmitted codeword if and only if d 2 t + 1. 3/9/2021 W J Martin Mathematical Sciences WPI

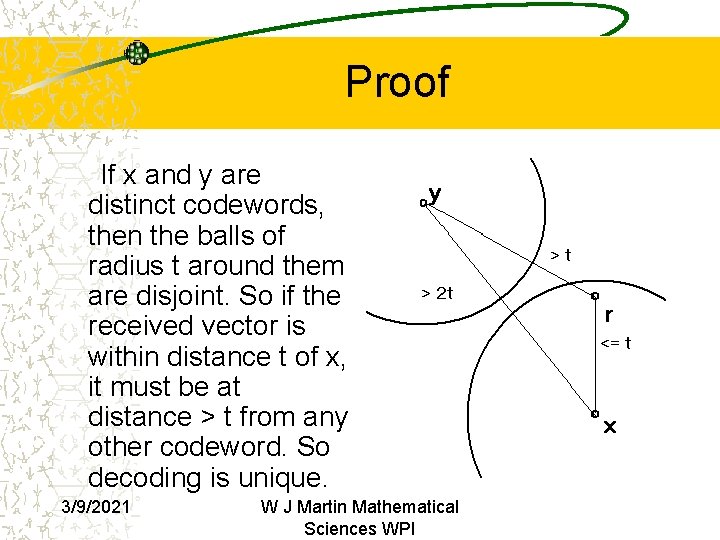
Proof If x and y are distinct codewords, then the balls of radius t around them are disjoint. So if the received vector is within distance t of x, it must be at distance > t from any other codeword. So decoding is unique. 3/9/2021 W J Martin Mathematical Sciences WPI

A Useful Extension of the Theorem The above (computationally infeasible) decoding algorithm also correctly recovers from any t symbol errors and any s symbol erasures provided d > 2 t+s. transmit: 0 1 1 2 2 3 0 receive: 0133? ? ? (here, t=2 errors and s=3 erasures) 3/9/2021 W J Martin Mathematical Sciences WPI

Small Example Let C denote the “rowspace” of the matrix Then C = { 000000, 110100, 011010, 101110, 001101, 111001, 010111, 100011 } and C has minimum distance 3 so C allows correction of any single-bit error in any transmitted codeword. 3/9/2021 W J Martin Mathematical Sciences WPI

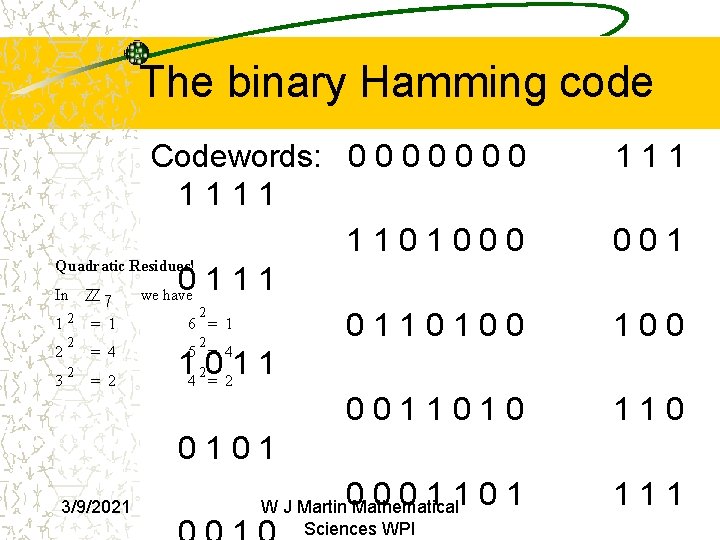
The binary Hamming code Codewords: 0 0 0 0 1111 1101000 Quadratic Residues! 0111 In ZZ 7 we have 2 12 = 1 6 = 1 0110100 2 2 2 = 4 5 = 4 14 20= 21 1 2 3 = 2 0011010 0101 001101 3/9/2021 W J Martin 0 Mathematical Sciences WPI 111 001 100 111

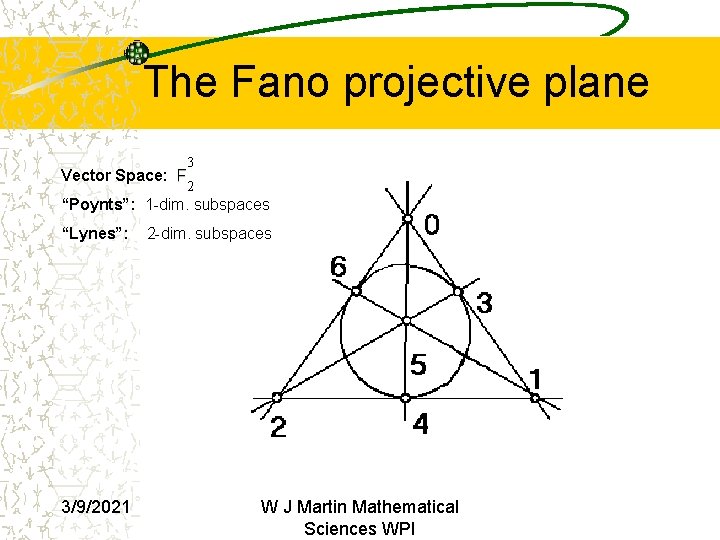
The Fano projective plane 3 Vector Space: F 2 “Poynts”: 1 -dim. subspaces “Lynes”: 3/9/2021 2 -dim. subspaces W J Martin Mathematical Sciences WPI

C = nullsp(H) where All codewords: 3/9/2021 0000000 1111111 0001111 1110000 011001100 0111100 1000011 10101010 1011010 0100101 110011001 1101001 0010110 W J Martin Mathematical Sciences WPI

Codes from polynomials Let’s replace F={0, 1} with F={0, 1, …, 6} (with modular arithmetic). Now consider the vector space F[z] of all polynomials in z with coefficients in F. For any subset N of F, we have a N linear transformation L: F[z] F via f(z) [ f(0), f(1), f(2), f(3), f(4), f(5) ] (Here, we use, N={0, 1, 2, 3, 4, 5}. ) This is a Reed-Solomon code. 3/9/2021 W J Martin Mathematical Sciences WPI

Polynomials to Codewords Example: Let the message be [1, 2, 2] (working 2 mod 7) Polynomial is f(z) = z + 2 Codeword is [f(0), f(1), f(2), f(3), f(4), f(5)] = [ 2, 5, 3, 3, 5, 2] 3/9/2021 W J Martin Mathematical Sciences WPI

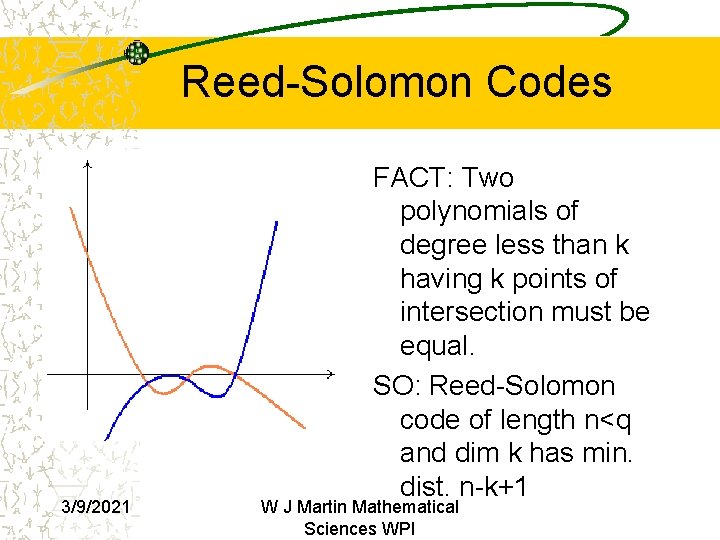
Reed-Solomon Codes 3/9/2021 FACT: Two polynomials of degree less than k having k points of intersection must be equal. SO: Reed-Solomon code of length n<q and dim k has min. dist. n-k+1 W J Martin Mathematical Sciences WPI

Compact Disc Parameters SONY/Philips design (1980) Music is sampled 44, 100 times per second Each sample consists of 32 bits, representing left and right channel signal magnitude 0— 65535 (Pulse Code Modulation – PCM) So chip must process 1, 411, 200 raw 3/9/2021 W J Martin Mathematical data bits per second Sciences WPI

Cross-Interleaved RS Codes Inner code is a 28 -dimensional subspace of a 32 -dimensional vector space over a finite field of size 256. Outer code is a 24 -dimensional subspace of a 28 -dimensional vector space. Six 32 -bit samples make up a 192 -bit frame which is encoded as a 224 -bit 3/9/2021 W J Martin Mathematical codeword. (Eventually, codewords have Sciences WPI

Encoding – The numbers The codewords from the first code are interleaved into a virtually infinite array of 28 rows of symbols over GF(256). We pull out 8 binary columns (one symbol) to obtain a 28 x 8=224 -bit frame which is then encoded using another Reed-Solomon code to obtain a codeword of length 256 bits. 3/9/2021 W J Martin Mathematical Sciences WPI

Interleaving to disperse errors Codewords of first code are stacked like bricks 28 rows of vectors over GF(256) Extract columns and re-encode using second Reed. Solomon code 3/9/2021 W J Martin Mathematical Sciences WPI

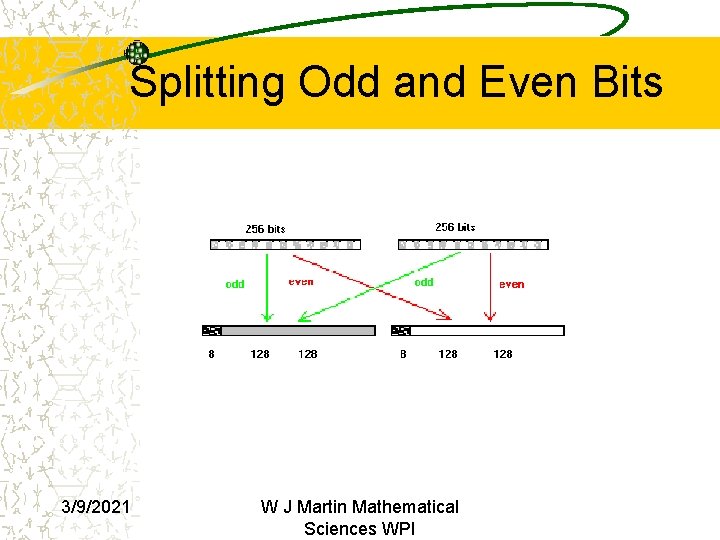
Splitting Odd and Even Bits 3/9/2021 W J Martin Mathematical Sciences WPI

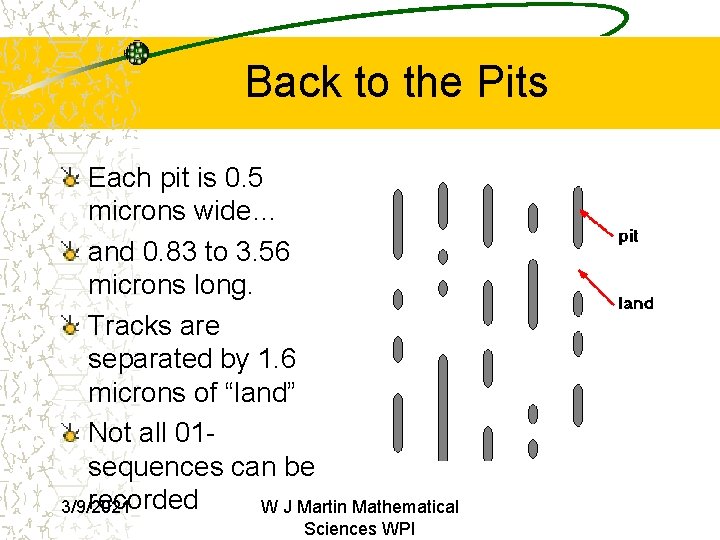
Back to the Pits Each pit is 0. 5 microns wide… and 0. 83 to 3. 56 microns long. Tracks are separated by 1. 6 microns of “land” Not all 01 sequences can be recorded 3/9/2021 W J Martin Mathematical Sciences WPI

EFM: Eight-to-Fourteen Modulation This encoding scheme can only store sequences where each consecutive pair of ones is separated by at least 2 and at 8 14 most 10 zeros 2 2 This is achieved by a mapping F F which is given by a lookup table. 3/9/2021 W J Martin Mathematical Sciences WPI

Further Processing Three more ‘merge bits’ are added to each of these 14 So 256+8=264=33 x 8 bits, carrying six samples, or 192 information bits, gets encoded as 588 channel bits on the disk This represents 0. 000136 seconds of music 3/9/2021 W J Martin Mathematical Sciences WPI

What actually goes on the disc? We must do this 7, 350 times per second So CD player reads 4, 321, 800 bits per second of music produced To get 74 minutes of music, we must store 74 x 60 x 4321800 = 19, 188, 792, 000 bits of data on the compact disc! 3/9/2021 W J Martin Mathematical Sciences WPI

When in doubt, erase Inner code has minimum distance 5 (over GF(256)) Rather than correct two-symbol errors, the CD just erases the entire received vector. 3/9/2021 W J Martin Mathematical Sciences WPI

So…how good is it? The two Reed-Solomon codes team up to correct ‘burst’ errors of up to 4000 consecutive data bits (2. 5 mm scratch on disc) If signal at time t cannot be recovered, interpolate With smart data distribution, this allows for recovery from burst errors of up to 12, 000 data bits (7. 5 mm track length on disc) If all else fails, Wmute, giving 0. 00028 sec of 3/9/2021 J Martin Mathematical Sciences WPI

Other Applications Space communications (Mariner, Voyager, etc. ) DVD, CD-ROM Cell phones, internet packets Memory: chips, hard drives, USB sticks RAID disk arrays Quantum computing 3/9/2021 W J Martin Mathematical Sciences WPI

The Last Slide Thank You All! 3/9/2021 W J Martin Mathematical Sciences WPI