THE MASTER EQUATION FOR THE REINFORCEMENT LEARNING Edgar








- Slides: 11

THE MASTER EQUATION FOR THE REINFORCEMENT LEARNING Edgar Vardanyan, David Saakian, Ricard Sole Moscow, 2019

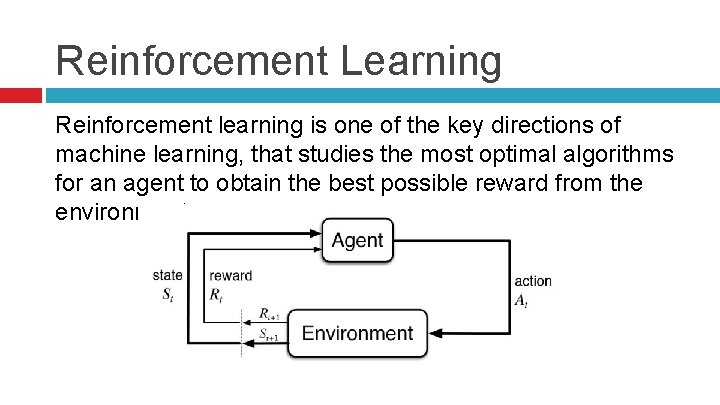
Reinforcement Learning Reinforcement learning is one of the key directions of machine learning, that studies the most optimal algorithms for an agent to obtain the best possible reward from the environment.

Q Learning

Choosing the action

Motivation The dynamics of the mean value of Q has been studied in many articles, but in order to have reliable system you need to study the variance of the Q vectors too. Thus you may know how much time does your system need in order to finish the learning process and may estimate the risks of your Y. Sato and J. P. Crutchfield, Physical Review E, 67, 015206 R system. (2003) A. Kianercy, and A. Galstyan, PRE, 88, 041145 (2012)

The Master equation approach The learning process is stochastic and we may need the Master equation approach to study the dynamics of the probability distribution of Q. To methods we tried solving this are the Hamilton Jacobi eqn. , the moment closing approximation and the Gaussian ansatz.

Hamilton Jacobi approach The Hamilton Jacobi equation is derived using the following steps.

Moment Closing Approximation For the second order moment closing approximation we try to express mean and variance of the distribution at every moment using those of the previous moments. After expressing mean and variance with the integrals of P(q, t) we obtain the following.

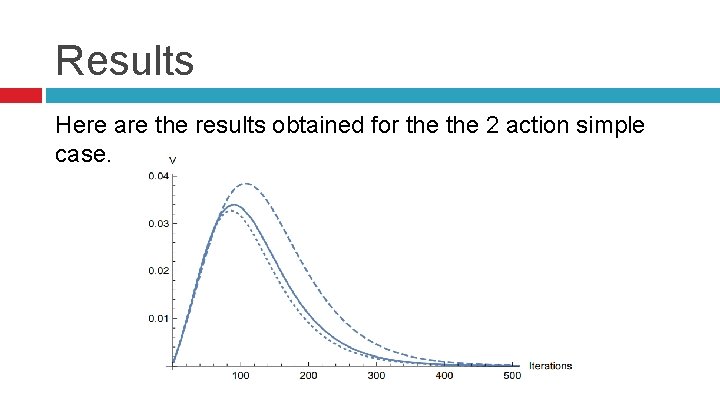
Results Here are the results obtained for the 2 action simple case.

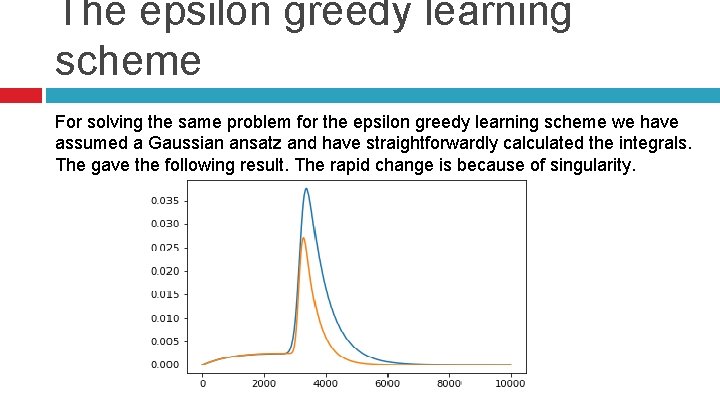
The epsilon greedy learning scheme For solving the same problem for the epsilon greedy learning scheme we have assumed a Gaussian ansatz and have straightforwardly calculated the integrals. The gave the following result. The rapid change is because of singularity.

Future Work Here is the list of what needs to be done in the future. 1) Apply the solution for more actions. 2) Apply the solution for varying/stochastic environment 3) Apply the solution for the games (2 agents competing against each other)