The Manhattan Tourist Problem Shane Wood 42908 CS

The Manhattan Tourist Problem Shane Wood 4/29/08 CS 329 E

Problem Summary • A tourist group in Manhattan wishes to see as many sights moving south-east from the corner of 59 th St. and 8 th Ave. to 42 nd Street and Lexington Ave. • How can we achieve this using dynamic programming?

Summary (cont. ) • Imagine the map as a graph with a source (59 th St. and 8 th Ave. ) and a sink ( 42 nd St. and Lexington Ave. : 45 th St 43 rd St 42 nd St Third Ave 47 th St Lexington Ave 49 th St Park Ave 51 st St Madison Ave 53 rd St 5 th Ave 55 th St 6 th Ave 57 th St 7 th Ave 8 th Ave 59 th St

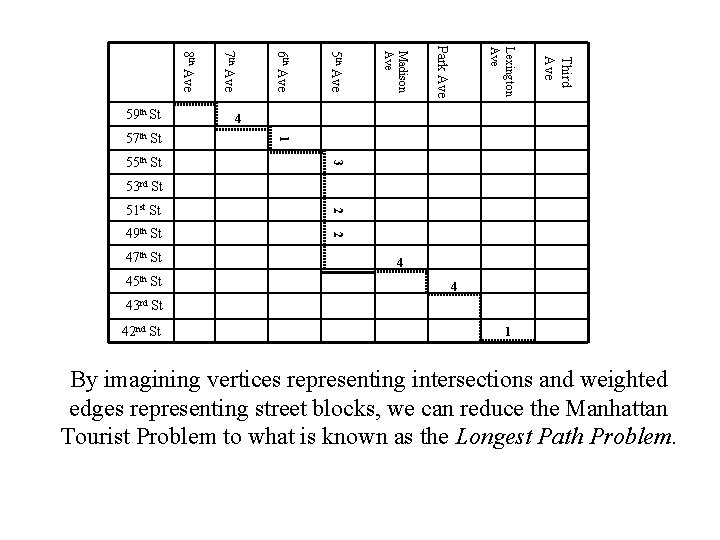
Third Ave Lexington Ave Park Ave Madison Ave 5 th Ave 4 1 3 55 th St 6 th Ave 57 th St 7 th Ave 8 th Ave 59 th St 53 rd St 51 st St 2 49 th St 2 47 th St 45 th St 4 4 43 rd St 42 nd St 1 By imagining vertices representing intersections and weighted edges representing street blocks, we can reduce the Manhattan Tourist Problem to what is known as the Longest Path Problem.

Manhattan Tourist Problem: • Input: A weighted grid G with a starting source vertex and an ending sink vertex • Output: A longest path in G from source to sink

Strategy • It is better to solve a generalized version of the MTP • Rather than solving the longest path from (0, 0) (source) to (n, m) (sink for an nxm grid), we will solve (0, 0) to (i, j) for 0 ≤ i ≤ n and 0 ≤ j ≤ m (an arbitrary vertex) • If (i, j) is a vertex in the longest path to the sink, the longest path to (i, j) must be contained in the longest path to the sink

Exhaustive Solution • Generate ALL possible paths in grid G • Output the longest path • Not feasible for even a moderately sized graph

A Greedy Algorithm • At every vertex, choose the adjacent edge with the highest weight • Easily achievable in polynomial time, but is unlikely to give the optimal solution, especially for larger graphs! Source 3 2 1 2 3 4 1 3 3 7 2 3 1 3 3 2 5 4 2 6 7 1 12 v 28 9 1 Sink

DP Approach • For every vertex, we want to find si, j, the weight of the longest path from (0, 0) to that vertex • Base Case: – Finding s 0, j and si, 0 for all i and j is easy S 0, j Si, 0 2 4 5 3 3 3 1 2 2 3 1 1 2 1 3 7 7 4 3 6 1 3 2 9

• The tourist can now arrive at (1, 1) in one of two ways: – Traveling south from (1, 0), or – Traveling east from (0, 1) • Once s 0, j and si, 0 are computed, we can determine s 1, 1 by comparing these two possibilities and determining the max – s 1, 1 = max s 0, 1 + weight of edge between (0, 1) and (1, 1) s 1, 0 + weight of edge between (1, 0) and (1, 1)

• This same logic applies more generally: – si, j = max si-1, j + weight of edge between (i-1, j) and (i, j) si, j-1 + weight of edge between (i, j-1) and (i, j) We can thus compute every value for si, j recursively with one run through the grid

Algorithm used for DP solution • Let wi, j represent the weight of a southerly move (the weight of the edge between (i, j-1) and (i, j) ) and wi, j represent the weight of an easterly move (the weight of the edge between (i-1, j) and (i, j) ) • 1 s 0, 0 0 • 2 for i 1 to n • 3 si, 0 si-1, 0 + wi, 0 • 4 for j 1 to n • 5 s 0, j-1 + w 0, j • 6 for i 1 to n • 7 for j 1 to m • 8 si, j max si-1, j + wi, j Running Time: O(nxm) for an si, j-1 + wi, j nxm grid • 9 return sn, m

Further analysis • Note that lines 1 -5 in the algorithm are generating the base cases we use to develop later recurrence relations • We can generate the longest path by keeping track of which paths are used to generate sn, m!

Questions? ? Thanks!