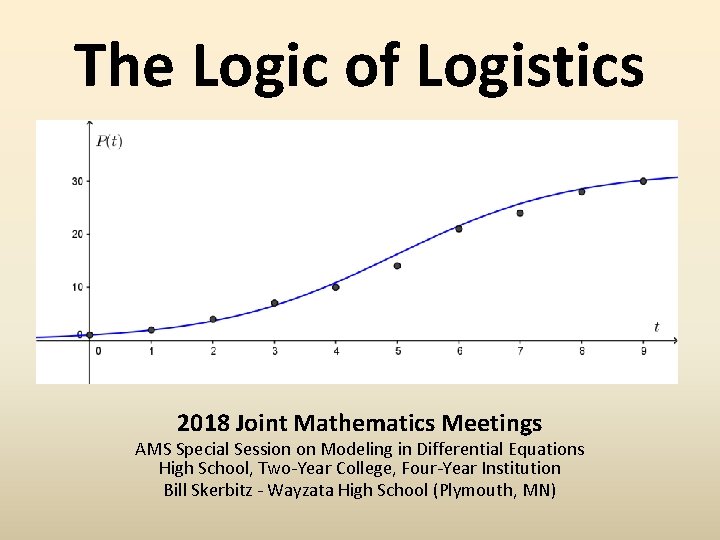
The Logic of Logistics 2018 Joint Mathematics Meetings














- Slides: 21

The Logic of Logistics 2018 Joint Mathematics Meetings AMS Special Session on Modeling in Differential Equations High School, Two-Year College, Four-Year Institution Bill Skerbitz - Wayzata High School (Plymouth, MN)

The Logic of Logistics – Typical Introductions to Logistic Functions Foerster, Paul. Precalculus with Trigonometry: Instructor’s Resource Book, Volume I © 2003 Key Curriculum Press.

https: //tinyurl. com/hc 3 noff Accessed 1/2/2018.

Demana, Finney, Kennedy, Waits. Calculus: Graphical, Numeric, Algebraic, 3 rd ed. © 2007. Pearson/Prentice Hall.

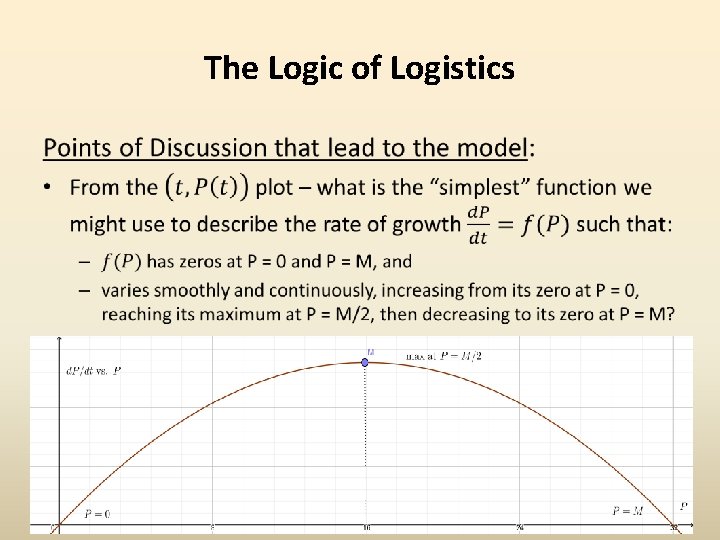
The Logic of Logistics •

The Logic of Logistics Simulation/Modeling assumptions: • Depending on time constraints – you can talk students through the assumptions: – One person (the “index case”? ) starts with the virus on day 0, i. e. , the I. C. is (0, 1). – Each carrier of the virus can pass the virus to at most one other person on a given day – Once a person has contracted the virus, they are no longer susceptible (i. e. , we wouldn’t count them again if our simulation indicates that they are re-infected with the virus; therefore, not every “interaction” results in a new infection) – Infection is never fatal (i. e. , the population never decreases)

The Logic of Logistics Simulation setup: • The students are numbered, in no particular order, from 1 to n, where n = # of people in the classroom (teacher participation mandatory? ) • Have some sort of tracking method (see table in subsequent slides) to track day and total # of individuals infected (it’s also helpful to keep a list of who’s been infected) – I use Geogebra to plot points in real time because it is easy to superimpose solution curves and slope fields later • The initial carrier is chosen randomly from the class, and all numbered participants stand up except for the initial carrier

The Logic of Logistics •

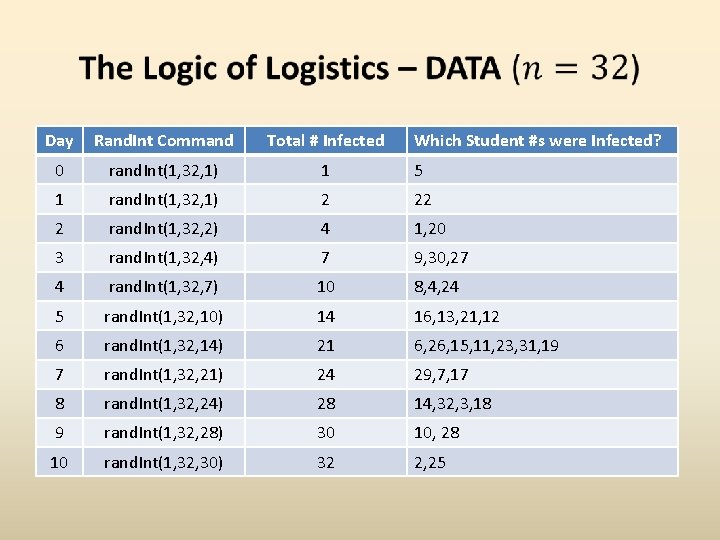
Day Rand. Int Command Total # Infected Which Student #s were Infected? 0 rand. Int(1, 32, 1) 1 5 1 rand. Int(1, 32, 1) 2 22 2 rand. Int(1, 32, 2) 4 1, 20 3 rand. Int(1, 32, 4) 7 9, 30, 27 4 rand. Int(1, 32, 7) 10 8, 4, 24 5 rand. Int(1, 32, 10) 14 16, 13, 21, 12 6 rand. Int(1, 32, 14) 21 6, 26, 15, 11, 23, 31, 19 7 rand. Int(1, 32, 21) 24 29, 7, 17 8 rand. Int(1, 32, 24) 28 14, 32, 3, 18 9 rand. Int(1, 32, 28) 30 10, 28 10 rand. Int(1, 32, 30) 32 2, 25

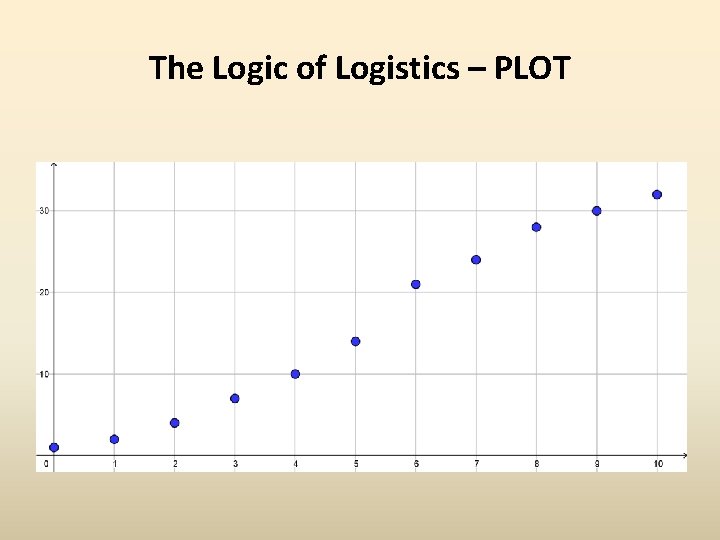
The Logic of Logistics – PLOT

The Logic of Logistics •

The Logic of Logistics •

The Logic of Logistics •

The Logic of Logistics •

The Logic of Logistics •

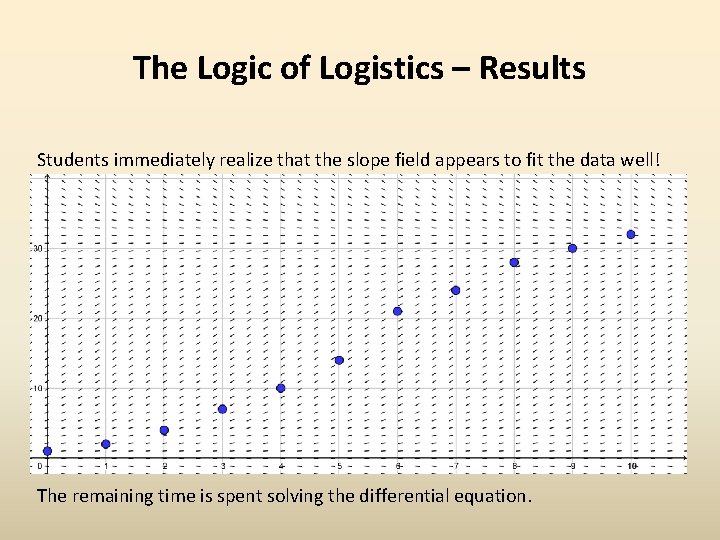
The Logic of Logistics – Results Students immediately realize that the slope field appears to fit the data well! The remaining time is spent solving the differential equation.

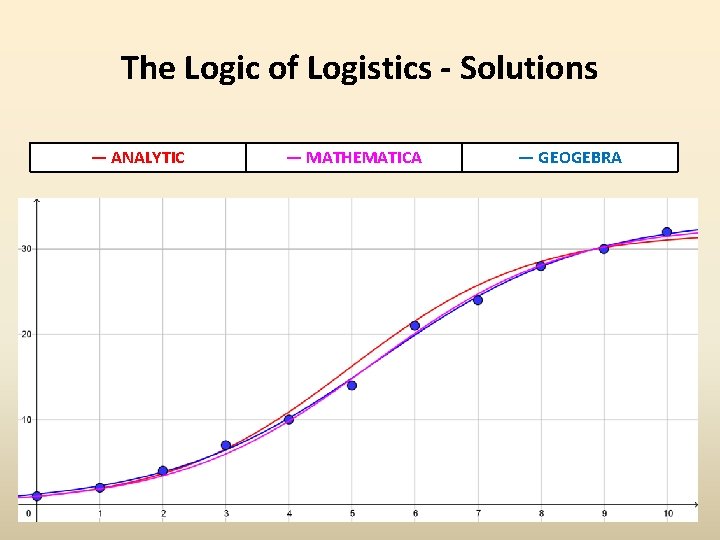
The Logic of Logistics - Solutions •

The Logic of Logistics - Solutions — ANALYTIC — MATHEMATICA — GEOGEBRA

The Logic of Logistics - Extensions •

The Logic of Logistics - Summary •

The Logic of Logistics Thank you for attending! 2018 Joint Mathematics Meetings AMS Special Session on Modeling in Differential Equations High School, Two-Year College, Four-Year Institution Bill Skerbitz - Wayzata High School (Plymouth, MN) Access this talk at mrskerbitz. com/JMM 2018 -Logistics. pdf.