The Logic Design Tool LDT A Graphical Method

The Logic Design Tool (LDT) A Graphical Method for Specifying Combinatorial and Sequential Logic Dave Mc. Farland Assurant Design Automation LLC Dave@Logic. Design. Tool. com Copyright © 2016 All rights reserved (The notes to these pages can be viewed by entering View > Notes Page from the menu) Version 6. 0

The Logic Design Tool (LDT) is a graphical aid for developing digital control. LDT identifies errors in the much less expensive, early design phase. It does this by providing multiple visualizations, interactive tests and analyses of the logic. It can then automatically generate optimized hardware or software source code in a variety of selectable implementations. LDT describes all relationships of a set of binary input variables and states to a set of output variables through a hierarchy of Karnaugh maps. The patented method extends the number of variables that can be used to implement combinatorial logic and increases the number of state transitions that can be practically included in sequential logic. This method allows LDT to generate a control specification that is complete (all conditions are specified) and unambiguous (only one action is possible for any one combination of variables). Because LDT will specify all transitions from all states for all input combinations, it can handle a much larger, more complex set of control problems and the specification is more likely to be free of errors.

Problem: Fixing logic errors during a production or fielded phase can be orders of magnitude more expensive than finding those errors during the initial design. Designing logic with more than four or five variables is prone to error, because the specification may not cover all desired conditions or may include unwanted actions. Truth tables, Binary Decision Diagrams (BDD) and Karnaugh maps can show all conditions and actions, but are cumbersome and subject to combinatorial explosion. Solution: Representing logic in a hierarchy of Karnaugh maps, where the hierarchy can be collapsed for don’t care conditions, enables all conditions to be specified, yet keeps the combinatorial explosion manageable.

LOGIC SPECIFICATION METHODS Text – Inexact and typically only covers apparent conditions. Boolean Equations - Difficult to understand reduce when logic includes more than four or five input variables. Truth tables - Do not show patterns that would be evident in a Karnaugh map. Tedious, subject to combinatorial explosion of cases. If, Then, Else Statements - Hidden or lost conditions are easily overlooked. Binary Decision Diagrams - Bit oriented, so visualizing the relationship to a larger number of variables is difficult. State Charts – Two dimensional, and do not account for the combinations of inputs necessary for each transition. Can become spaghetti charts. Entered Variables – Reducing the size of the map can introduce human error. Logic Design Tool - Can specify all transitions from all states for all input combinations. If no states are needed, can specify combinatorial logic.

LEVELS OF ABSTRACTION IN DESIGN AUTOMATION Higher Level LDT Non-Boolean Equation Entry and Display Executable Specification Any State to Any Subset of States Transition State Analysis View All Input Combinations, All States Worst, Best and Sneak Path Execution Selectable Degree of Rigor Logic Reduction to Sum of Products Transform Exhaustive Test Driver Generation State Charts Finite State Machine Visualization Substate Grouping Semi-Automated Source Code Generation Source Code Compiler Assembly Code Compiler Lower Level Manual Machine Code Insertion

LDT CAPABILITIES NOT FOUND IN OTHER TOOLS - Specify logic that is complete and unambiguous without the use of equations. - Represent combinatorial, sequential and asynchronous logic. - Find the worst and best case execution paths, accumulated time on given path. - Generate exhaustive set of test vectors for all paths. - Easily show a transition from any state to many or all states. - Display a large (greater than 16) number of states and transitions on a readable diagram without grouping substates. - Make the software implemented state machine or combinatorial logic table driven so its behavior can be changed without recompilation of the code. - Find the near minimal state machine implementation for speed or number of gates with a report of the rationale behind the reduction.

STATEMENT OF NEED

WHY SPECIFY ALL STATES, ALL TRANSITIONS, ALL CONDITIONS? Needed for applications that are: Safety Critical – Behavior under all combinations of failures must be known. (aircraft control, man-rated environments, high value systems, nuclear plant). Data Secure - Classified data levels must not be mixed or compromised. (encryption devices, multilevel secure boxes, network security). Subject to Litigation – Systems must not execute dangerous actions. (medical equipment, transportation, financial transactions). Require reduction, lack of errors - Logic must be small, cheap, reliable, easily manufactured. (large quantity consumer items).

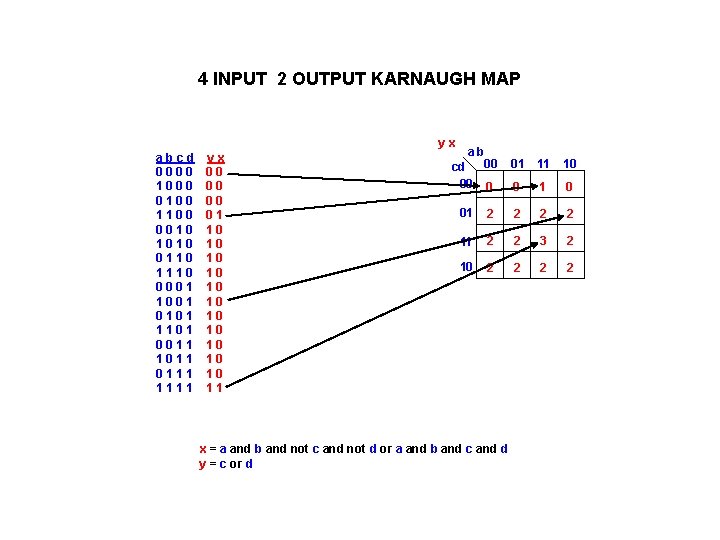
4 INPUT 2 OUTPUT KARNAUGH MAP yx abcd 0000 1000 0100 1100 0010 1010 0110 1110 0001 1001 0101 1101 0011 1011 0111 1111 yx 00 00 00 01 10 10 10 11 ab 00 cd 00 0 01 11 10 0 1 0 01 2 2 11 2 2 3 2 10 2 2 x = a and b and not c and not d or a and b and c and d y = c or d

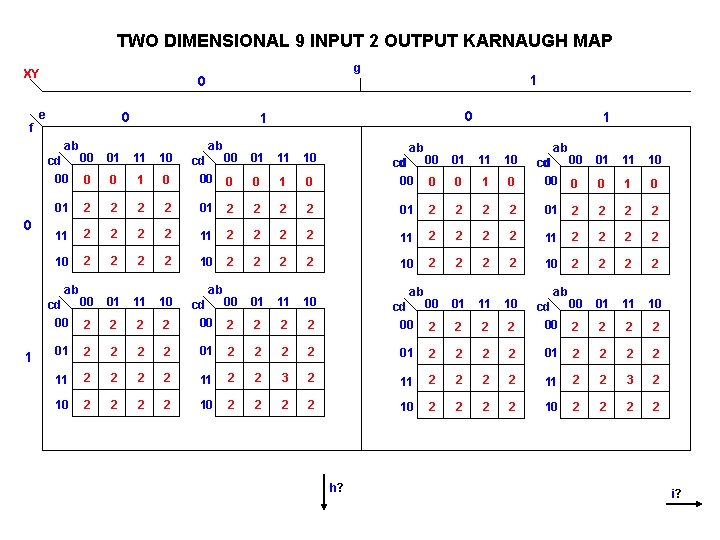
TWO DIMENSIONAL 9 INPUT 2 OUTPUT KARNAUGH MAP XY f 0 e 0 ab 0 1 ab cd 00 00 01 11 10 0 0 1 0 01 2 2 01 11 2 2 10 2 2 cd 00 00 01 11 10 2 2 2 2 01 11 2 2 10 2 2 ab 1 g 00 cd 00 0 ab 00 cd d 00 0 01 11 10 0 1 0 2 2 01 11 2 2 10 2 2 01 11 10 2 2 2 2 01 11 2 2 3 2 10 2 2 ab 00 cd 00 2 h? 1 ab 00 cd d 00 0 01 11 10 0 1 0 2 2 01 2 2 2 2 11 2 2 2 2 10 2 2 ab 00 cd 00 2 01 11 10 2 2 2 2 2 01 2 2 2 2 11 2 2 3 2 10 2 2 2 2 ab 00 cd 00 2 i?

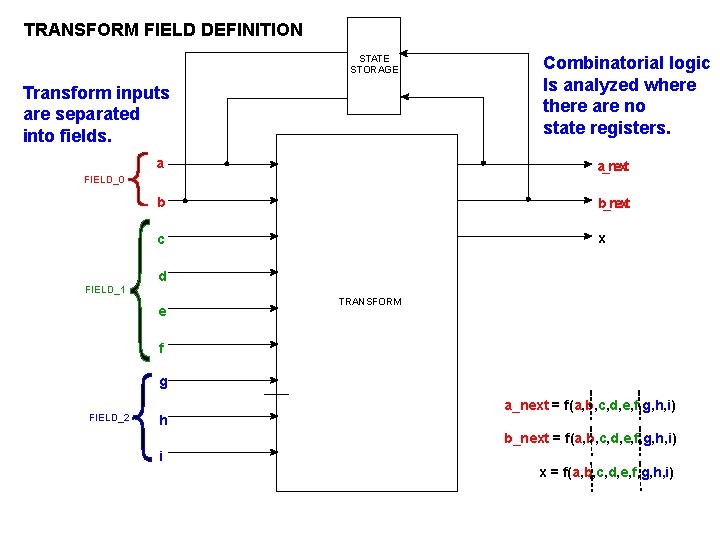
TRANSFORM FIELD DEFINITION STATE STORAGE Transform inputs are separated into fields. Combinatorial logic Is analyzed where there are no state registers. a a_next b b_next c x FIELD_0 d FIELD_1 e TRANSFORM f g FIELD_2 h a_next = f(a, b, c, d, e, f, g, h, i) b_next = f(a, b, c, d, e, f, g, h, i) i x = f(a, b, c, d, e, f, g, h, i)

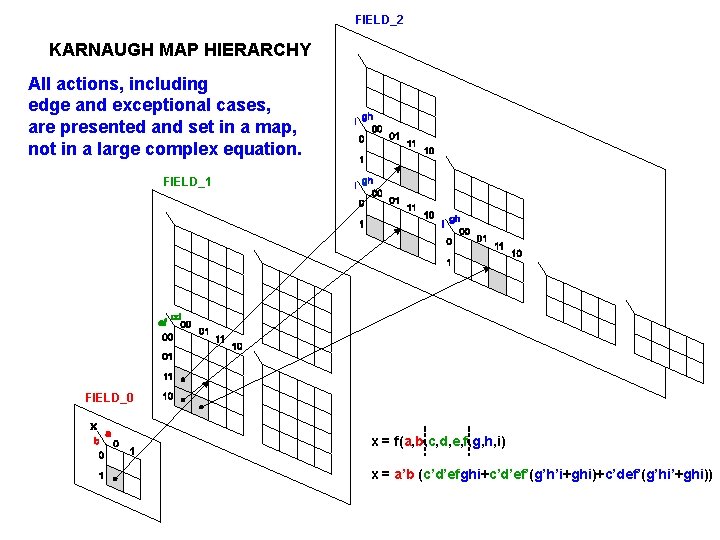
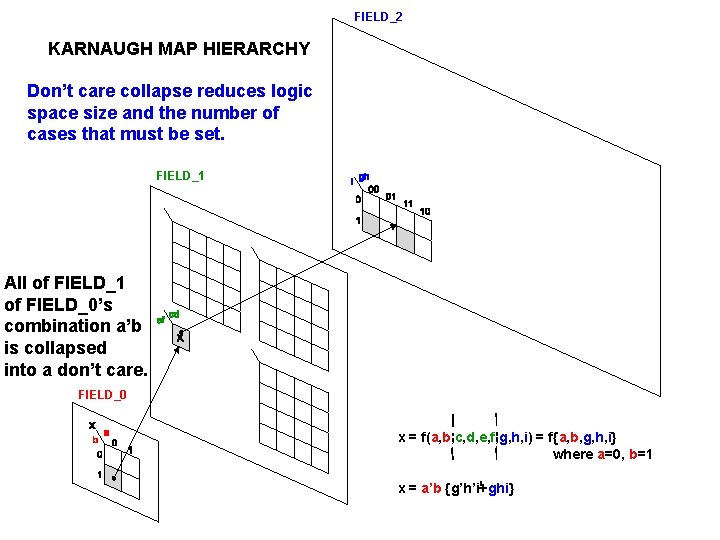
FIELD_2 KARNAUGH MAP HIERARCHY All actions, including edge and exceptional cases, are presented and set in a map, not in a large complex equation. FIELD_1 FIELD_0 x = f(a, b, c, d, e, f, g, h, i) x = a’b (c’d’efghi+c’d’ef’(g’h’i+ghi)+c’def’(g’hi’+ghi))

FIELD_2 KARNAUGH MAP HIERARCHY Don’t care collapse reduces logic space size and the number of cases that must be set. FIELD_1 All of FIELD_1 of FIELD_0’s combination a’b is collapsed into a don’t care. FIELD_0 x = f(a, b, c, d, e, f, g, h, i) = f{a, b, g, h, i} where a=0, b=1 x = a’b {g’h’i+ghi}

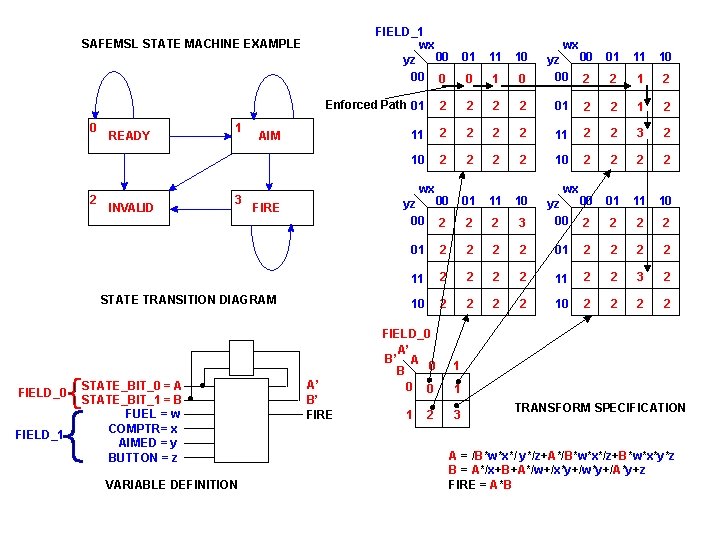
IMPLEMENTATION EXAMPLES Three missile control state machine examples with very different behavior. SAFEMSL – A ballistic missile which must be fail safe and must fire only when the correct sequence of commands is entered, otherwise it must halt. SUREMSL – A tactical missile used to protect a jet while engaged in a dogfight. Preferably the missile would follow the correct sequence, but under most conditions must fire if pilot pushes button. Each has four binary control inputs: FUEL, COMPTR, AIMED, BUTTON Each has four states: READY, AIM, INVALD, FIRE States are defined by two bits: STATE_BIT_0, STATE_BIT_1 Inputs to the next state transform are divided into two fields: state FIELD_0 of A and B, and an input FIELD_1 of w, x, y, z. CPLXMSL – An actual missile launch controller used for battleship defense. This has 16 states and five inputs and is described in the manual.

FIELD_1 wx 00 yz 00 0 SAFEMSL STATE MACHINE EXAMPLE 0 2 1 READY 3 INVALID FIELD_1 STATE_BIT_0 = A STATE_BIT_1 = B FUEL = w COMPTR= x AIMED = y BUTTON = z . . VARIABLE DEFINITION 11 10 0 1 0 wx 00 yz 00 2 01 11 10 2 1 2 Enforced Path 01 2 2 11 2 2 3 2 10 2 2 2 2 wx 00 yz 00 2 01 11 10 2 2 3 wx 00 yz 00 2 2 AIM FIRE STATE TRANSITION DIAGRAM FIELD_0 01 A’ B’ FIRE 01 2 2 2 2 11 2 2 3 2 10 2 2 2 2 FIELD_0 A’ B’ A 0 B 1 0 0 1 1 2 3 TRANSFORM SPECIFICATION A = /B*w*x*/ y*/z+A*/B*w*x*/z+B*w*x*y*z B = A*/x+B+A*/w+/x*y+/w*y+/A*y+z FIRE = A*B

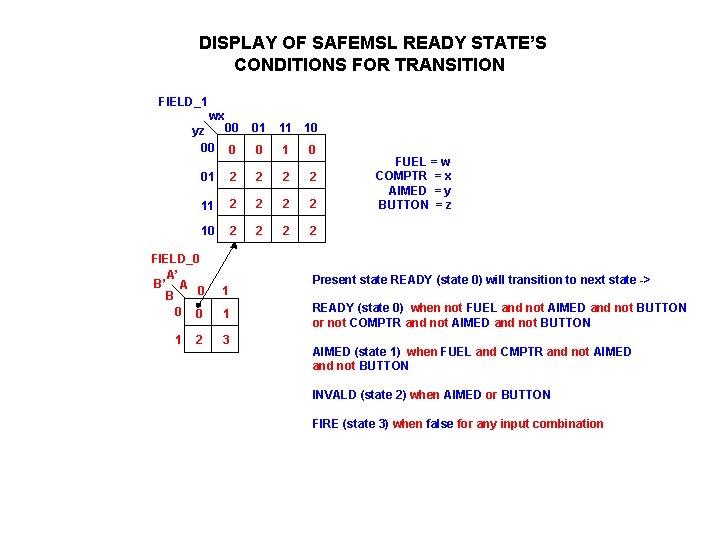
DISPLAY OF SAFEMSL READY STATE’S CONDITIONS FOR TRANSITION FIELD_1 wx 00 yz 00 0 01 11 10 0 1 0 01 2 2 2 2 10 2 2 FIELD_0 A’ B’ A 0 B 1 0 0 1 1 2 3 FUEL = w COMPTR = x AIMED = y BUTTON = z Present state READY (state 0) will transition to next state -> READY (state 0) when not FUEL and not AIMED and not BUTTON or not COMPTR and not AIMED and not BUTTON AIMED (state 1) when FUEL and CMPTR and not AIMED and not BUTTON INVALD (state 2) when AIMED or BUTTON FIRE (state 3) when false for any input combination

SAFMSL STATE MACHINE SOURCE CODE -SECURITY CLASSIFICATION -- ****************************** -CSCI_TITLE -PACKAGE spec -CSC Transform -- DESCRIPTION: -- This package spec provides the interface to -- package safemsl implements a state -- machine composed of 4 inputs, 4 states and -- 1 outputs. -- The procedure Transition calculates the next state -- based upon the inputs and the present value of State. ----- The procedure Transition calculates the next state -- based upon the inputs and the present value of State. -- The value of State must be initialized and maintained by -- each caller. --- REFERENCES: -- none -- EXCEPTION HANDLING AND ERROR PROCESSING: -- none -- LIMITATIONS: -- none -- WAIVERS: -- none -- MODIFICATIONS: -- NUMBER DATE RSE DESCRIPTION -- 1. 0 64992/64876/0 -- CODE CLASSIFICATION: -- Not yet given a classification. -- ****************************** package safemsl is Number_inputs Number_outputs Number_state_bits Number_states : constant : = 4; : constant : = 1; : constant : = 2; : constant : = (2**Number_state_bits); subtype Input_range is integer range 0. . (Number_inputs - 1); subtype Output_range is integer range 0. . (Number_outputs - 1); type State_range is range 0. . (Number_states - 1); subtype Index_range is integer range 0. . 1; type Input_type is array(Input_range) of integer range 0. . 1; type Output_type is array(Output_range) of integer range 0. . 1; subtype State_type is integer range 0. . (Number_states - 1); procedure Transition(Input State Outputs end safemsl; : in Input_type ; : in out State_type; : out Output_type);

SAFEMSL DOCUMENTATION ARTIFACTS 1. 0 Specification Description 2. 0 Input To Output, State Bit Transform 3. 0 Finite State Machine Karnaugh Maps 3. 1 State 3. 2 Intermediate 3. 3 Transition 4. 0 Source code Files 4. 1 Ada 4. 1. 1 Specification 4. 1. 2 Body 4. 1. 3 Interactive Driver 4. 1. 4 Exhaustive Unit Test Driver 4. 2 VHDL 4. 3 C 4. 4 Driver 4. 5 Body 5. 0 Espresso Formated Truth Table 6. 0 State and Output Bit Model 7. 0 State Analysis

LDT USER SELECTIONS Specification Entry Methods: Default, Single Entry, Transition Boolean, Output Bit Boolean, Next State Bit Boolean, Don’t Care, Test Vector, Truth Table, espresso Alternate Views: Truth Table, If-Then-Else, Case, STD, Timing Diagrams, Boolean Equations, Karnaugh Map Patterns, Hierarchy Analysis: Interactive Debugger, Dead, Hanging, No Decision States, Worst, Best Case Execution Paths, Logic Reduction Report Source Code Output: C, Pascal, Ada, Assembly, VHDL, espresso, with test drivers, exhaustive test vector set and complete document artifacts. Transform Implementations: Boolean Equation, Software Array, If-then-else, Case Reverse Engineer: VHDL, espresso

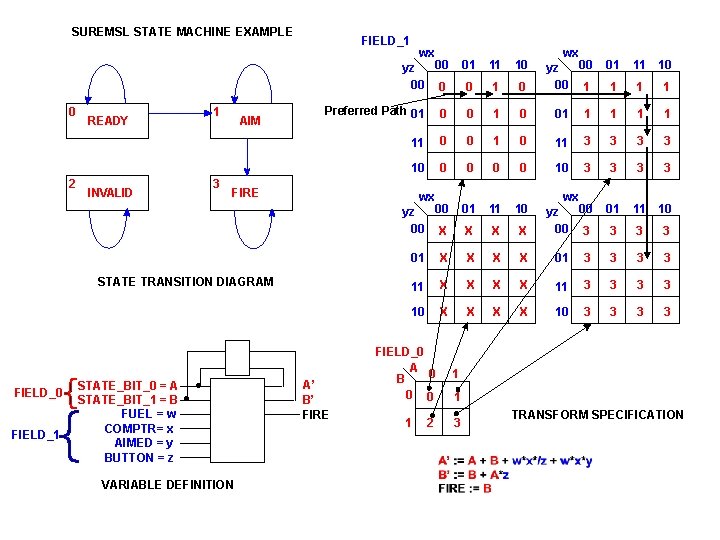
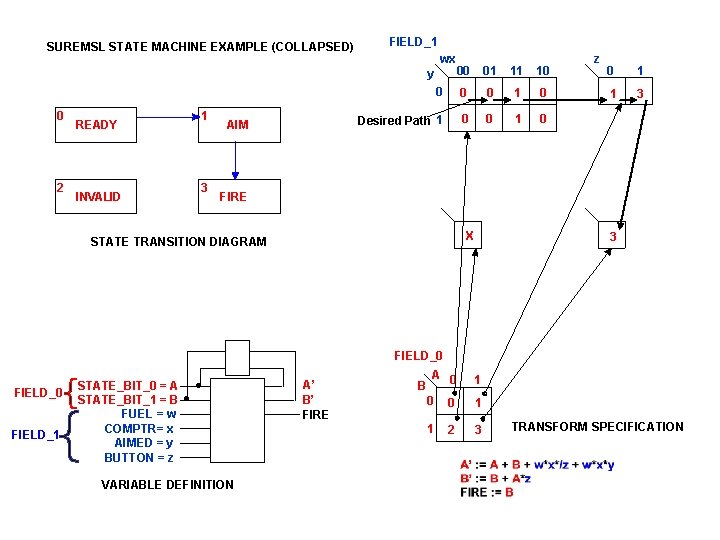
SUREMSL STATE MACHINE EXAMPLE FIELD_1 wx 00 yz 00 0 0 2 1 READY 3 INVALID AIM FIELD_0 FIELD_1 VARIABLE DEFINITION 10 0 1 0 wx 00 yz 00 1 01 11 10 1 1 1 0 01 1 1 11 0 0 11 3 3 10 0 0 10 3 3 yz 00 00 01 11 10 X X 00 yz 00 3 3 01 X X 01 3 3 11 X X 11 3 3 10 X X 10 3 3 FIRE . . 11 Preferred Path 01 wx STATE TRANSITION DIAGRAM STATE_BIT_0 = A STATE_BIT_1 = B FUEL = w COMPTR= x AIMED = y BUTTON = z 01 A’ B’ FIRE FIELD_0 A 0 B 0 0 1 1 3 2 wx 1 TRANSFORM SPECIFICATION

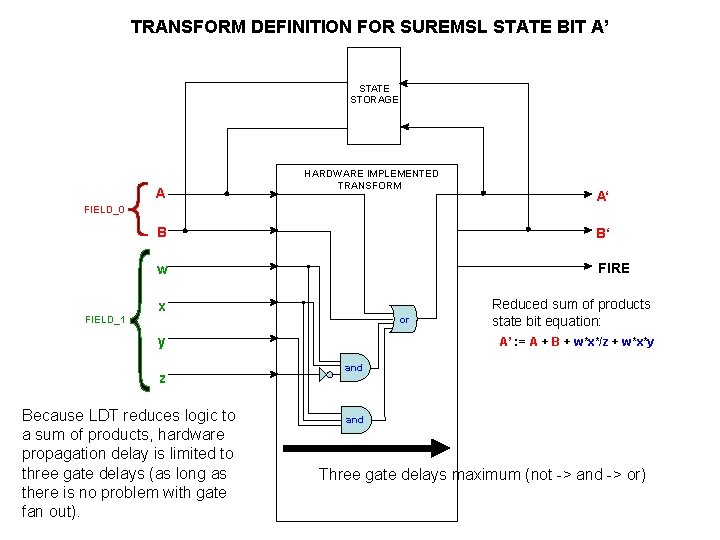
TRANSFORM DEFINITION FOR SUREMSL STATE BIT A’ STATE STORAGE A HARDWARE IMPLEMENTED TRANSFORM FIELD_0 B B‘ . w x FIRE . or FIELD_1 y z Because LDT reduces logic to a sum of products, hardware propagation delay is limited to three gate delays (as long as there is no problem with gate fan out). A‘ Reduced sum of products state bit equation: A’ : = A + B + w*x*/z + w*x*y and Three gate delays maximum (not -> and -> or)

SUREMSL STATE MACHINE EXAMPLE (COLLAPSED) FIELD_1 wx 00 01 11 10 0 1 0 Desired Path 1 0 0 1 0 y 0 2 READY INVALID 1 3 AIM FIELD_0 FIELD_1 0 1 1 3 FIRE X STATE TRANSITION DIAGRAM STATE_BIT_0 = A STATE_BIT_1 = B FUEL = w COMPTR= x AIMED = y BUTTON = z z . . VARIABLE DEFINITION 3 FIELD_0 A’ B’ FIRE B A 0 1 0 0 1 1 2 3 TRANSFORM SPECIFICATION

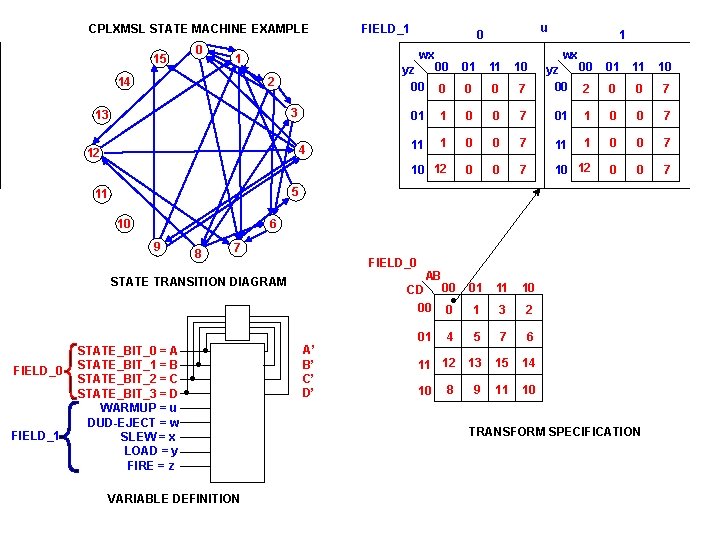
CPLXMSL STATE MACHINE EXAMPLE 15 0 2 3 13 4 12 10 wx yz 00 00 01 11 10 00 yz 00 2 01 11 10 0 7 01 1 0 0 7 11 1 0 0 7 10 12 0 0 7 01 11 10 1 3 2 4 5 7 6 11 12 13 15 14 8 9 11 10 6 9 8 7 FIELD_0 STATE TRANSITION DIAGRAM FIELD_1 1 5 11 FIELD_0 u 0 wx 1 14 FIELD_1 STATE_BIT_0 = A STATE_BIT_1 = B STATE_BIT_2 = C STATE_BIT_3 = D WARMUP = u DUD-EJECT = w SLEW = x LOAD = y FIRE = z . . VARIABLE DEFINITION AB . CD 00 00 0 A’ B’ C’ D’ 01 10 TRANSFORM SPECIFICATION

CPLXMSL STATE MACHINE EXAMPLE Next State Analysis Report of search for states which are hanging (no states transition to this state) or dead end (no states transition from this state). State number 10 named State 10 is hanging. State number 10 named State 10 is a dead end state. State number 11 named State 11 is hanging. State number 11 named State 11 is a dead end state. State number 13 named State 13 is hanging. State number 13 named State 13 is a dead end state. State number 14 named State 14 is hanging. State number 14 named State 14 is a dead end state. State number 15 named State 15 is a dead end state.

CPLXMSL STATE MACHINE EXAMPLE Next State Equation for Least Significant (0) State Bit

CONCLUSION LDT can specify all transitions from all states for all input combinations. Because of LDT’s higher degree of rigor, and its additional visibility into the specification, it increases the chance of finding logic faults early in the inexpensive design phase. Specifications are debugged interactively and implementation is automated, reducing the chance for human error and speeding development time. The amount of rigor and the size of collapsible don’t care space is user selectable and can be tailored to meet system needs. LDT handles the more general case of logic (no input priority, all inputs arrive at the same time, both sequential, combinatorial and asynchronous use). LDT has many options that make it a valuable fit for a broad set of applications.

BACKUP CHARTS

TOOL METRICS 23000 lines of code. 76 User Options. 150 Page User Manual. Using LDT, the complex missile example implemented and tested in 3 hours code that is claimed to have taken 2 months to develop and install with normal coding methods. The specification size grows linearly with complexity, not exponentially with number of inputs, states. Ada source output meets Software Productivity Consortium coding standards. LDT is patent protected. (US Patent # 6, 898, 563).

MY BACKGROUND 9 years at Boeing, Fault Tolerant Flight Control Lab, Seattle 5 years at United Technology Corporation, Advanced Development, San Diego 10 Years at Lockheed, F-22 Embedded Software Engineer, Marietta 2 patents - Triply Redundant Flight Control Selector, Logic Design Tool

FUTURE USER OPTIONS VHDL output compiled. BDD output and display. Select array or Turing Machine for transform. Reliability of hardware for levels of redundancy. Execution paths accumulated. Output compatible with BOOZER logic minimizer, ADAM design software, Berkley PLA format, A-OPS design software. Detect loops, no-decision states. Interactive Tutorial. Parse and display control logic (if-then-else, case, for loops) of existing code. Cut and paste regions of logic space.

ILLUSTRATIVE EXAMPLES Safelmsl, Suremsl, Cplxmsl Seven Segment Numeric Display Up, Down Counter Triplex Flight Control System Channel Selector Hex to Decimal Converter Cruise Control Network Protocol

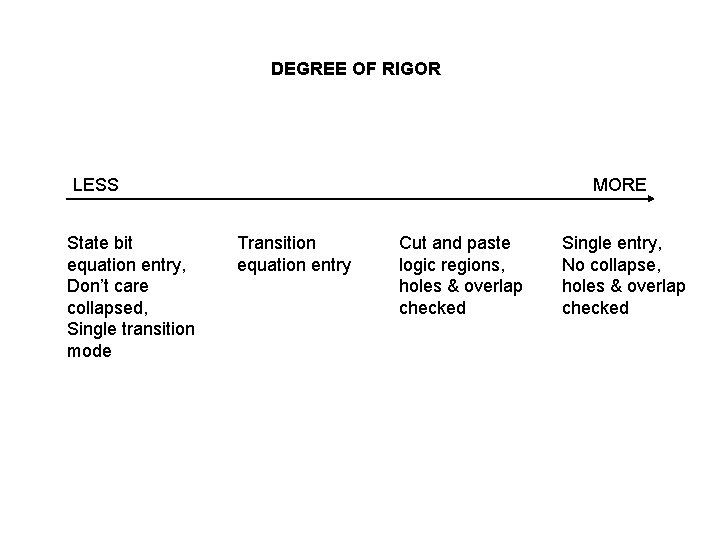
DEGREE OF RIGOR LESS State bit equation entry, Don’t care collapsed, Single transition mode MORE Transition equation entry Cut and paste logic regions, holes & overlap checked Single entry, No collapse, holes & overlap checked

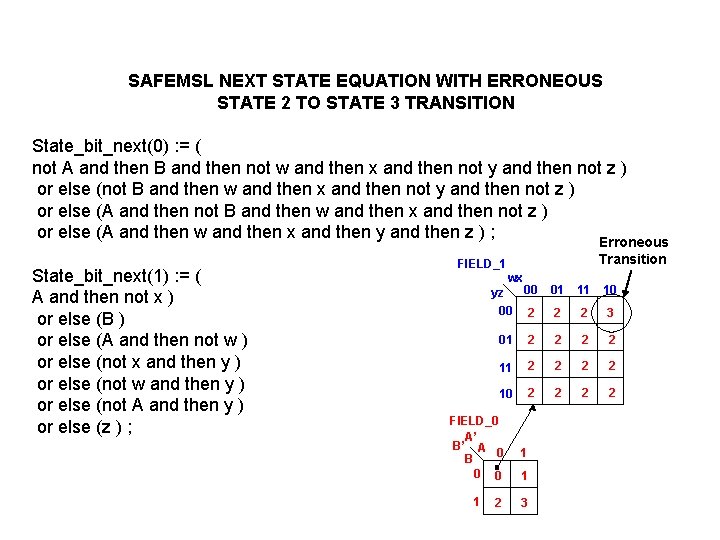
SAFEMSL NEXT STATE EQUATION WITH ERRONEOUS STATE 2 TO STATE 3 TRANSITION State_bit_next(0) : = ( not A and then B and then not w and then x and then not y and then not z ) or else (not B and then w and then x and then not y and then not z ) or else (A and then not B and then w and then x and then not z ) or else (A and then w and then x and then y and then z ) ; Erroneous State_bit_next(1) : = ( A and then not x ) or else (B ) or else (A and then not w ) or else (not x and then y ) or else (not w and then y ) or else (not A and then y ) or else (z ) ; Transition FIELD_1 wx 00 yz 00 2 01 11 10 2 2 3 01 2 2 2 2 10 2 2 FIELD_0 A’ B’ A 0 B 1 0 0 1 1 2 3

SAFEMSL NEXT STATE EQUATION WITH NO ERROR State_bit_next(0) : = ( not B and then w and then x and then not y and then not z ) or else (A and then not B and then w and then x and then not z ) or else (A and then w and then x and then y and then z ) ; State_bit_next(1) : = ( A and then not x ) or else (B ) or else (A and then not w ) or else (not x and then y ) or else (not w and then y ) or else (not A and then y ) or else (z) ; Correct Transition FIELD_1 wx 00 yz 00 2 01 11 10 2 2 2 01 2 2 2 2 10 2 2 FIELD_0 A’ B’ A 0 B 1 0 0 1 1 2 3

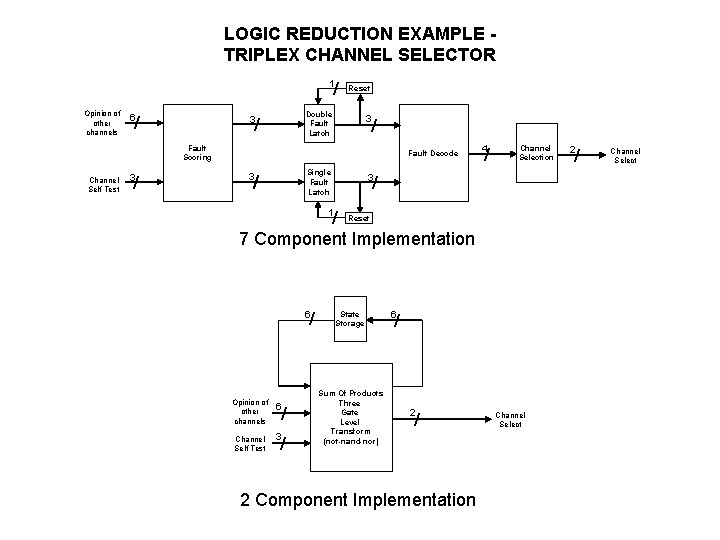
LOGIC REDUCTION EXAMPLE TRIPLEX CHANNEL SELECTOR 1 / Opinion of other channels 6 / Reset Double Fault Latch 3 / Fault Scoring Channel Self Test 3 / Fault Decode Single Fault Latch 3 / 4 / Channel Selection 3 / 1 / Reset 7 Component Implementation 6 / Opinion of other channels 6 Channel Self Test 3 / / State Storage Sum Of Products Three Gate Level Transform (not-nand-nor) 6 / 2 Component Implementation Channel Select 2 / Channel Select

A LARGER NUMBER OF MINTERMS IN A BOOLEAN EQUATION CAN INDICATE AN ENTRY ERROR x ab 00 cd 00 1 01 11 10 1 1 1 x ab 00 cd 00 0 01 11 10 1 1 1 01 1 1 11 0 0 0 0 10 0 0 x = not c x = a and not c or b and not c or not c and d

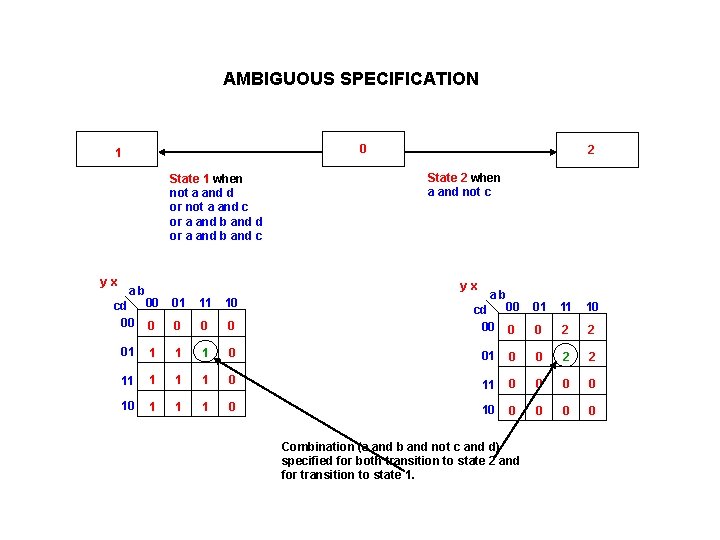
AMBIGUOUS SPECIFICATION 0 1 State 1 when not a and d or not a and c or a and b and d or a and b and c yx 2 State 2 when a and not c yx ab 00 cd 00 0 01 11 10 0 2 2 01 1 0 01 0 0 2 2 11 1 0 11 0 0 10 1 1 1 0 10 0 0 Combination (a and b and not c and d) specified for both transition to state 2 and for transition to state 1.

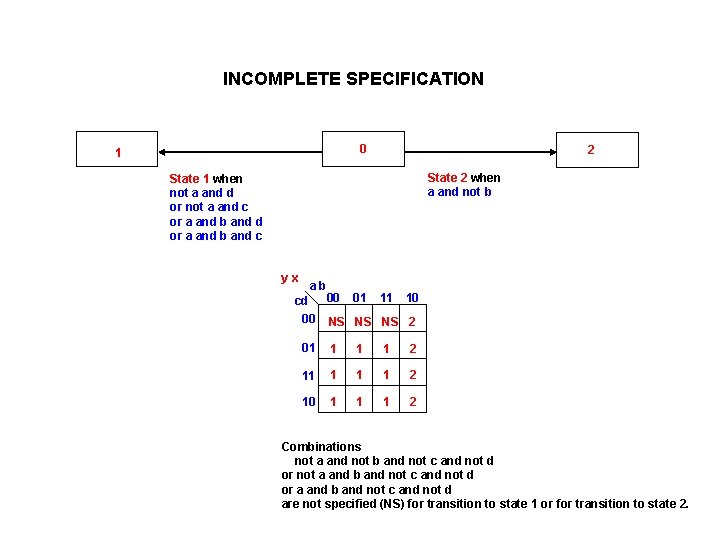
INCOMPLETE SPECIFICATION 0 1 2 State 2 when a and not b State 1 when not a and d or not a and c or a and b and d or a and b and c yx ab 00 01 11 10 cd 00 NS NS NS 2 01 1 1 1 2 10 1 1 1 2 Combinations not a and not b and not c and not d or not a and b and not c and not d or a and b and not c and not d are not specified (NS) for transition to state 1 or for transition to state 2.

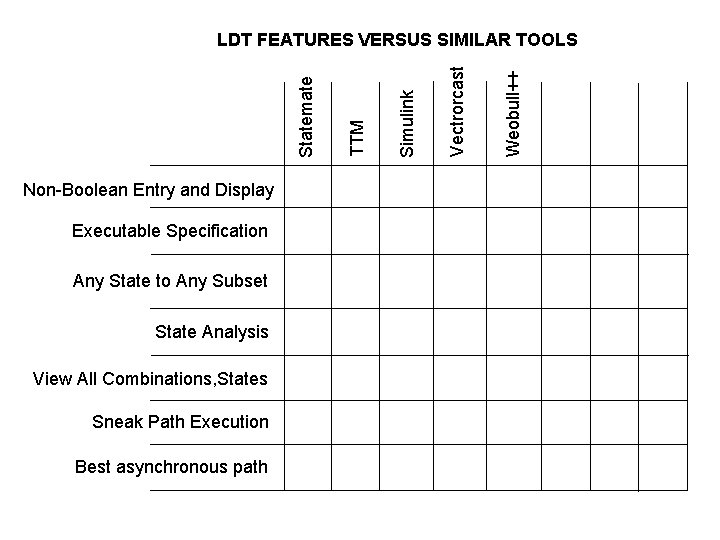
Non-Boolean Entry and Display Executable Specification Any State to Any Subset State Analysis View All Combinations, States Sneak Path Execution Best asynchronous path Weobull++ Vectrorcast Simulink TTM Statemate LDT FEATURES VERSUS SIMILAR TOOLS

GOVERNMENT AGENCY CERTIFICATIONS

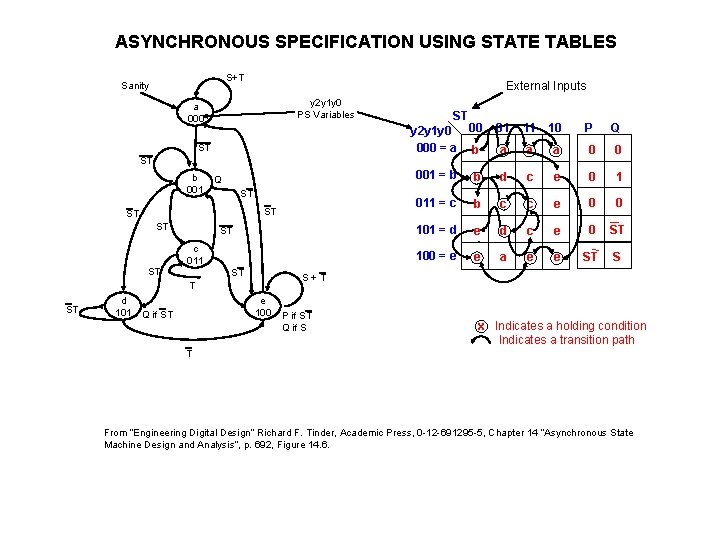
ASYNCHRONOUS SPECIFICATION USING STATE TABLES S+T Sanity External Inputs y 2 y 1 y 0 PS Variables a 000 ST ST y 2 y 1 y 0 000 = a 00 01 11 10 P Q b a a a 0 0 001 = b b d c e 0 1 011 = c b c c e 0 0 101 = d e d c e 0 ST 100 = e e a e e ST S ST b 001 Q ST ST ST c 011 ST ST S+T T ST d 101 Q if ST e 100 P if ST Q if S x Indicates a holding condition Indicates a transition path T From “Engineering Digital Design” Richard F. Tinder, Academic Press, 0 -12 -691295 -5, Chapter 14 “Asynchronous State Machine Design and Analysis”, p. 692, Figure 14. 6.

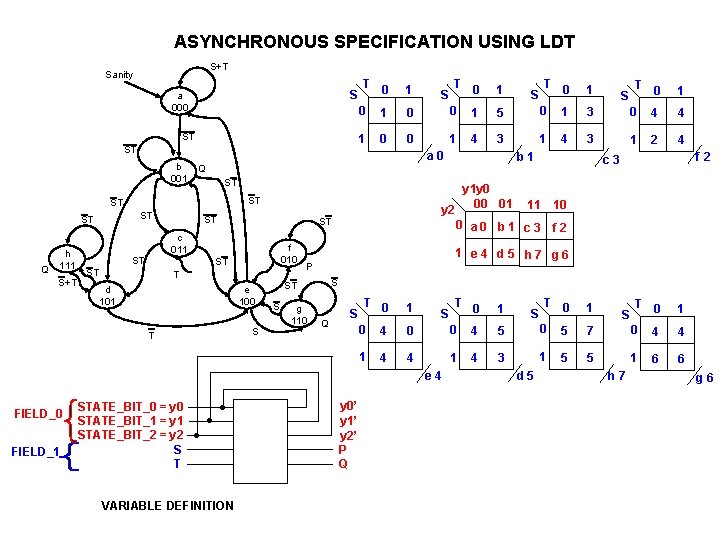
ASYNCHRONOUS SPECIFICATION USING LDT S+T Sanity S a 000 ST ST b 001 Q h 111 S+T FIELD_1 f 010 ST T d 101 e 100 S STATE_BIT_0 = y 0 STATE_BIT_1 = y 1 STATE_BIT_2 = y 2 S T . . . VARIABLE DEFINITION g 110 1 S T 0 1 5 0 1 3 0 4 4 1 0 0 1 4 3 1 2 4 b 1 f 2 c 3 y 1 y 0 00 01 11 y 2 0 a 0 b 1 c 3 10 f 2 1 e 4 d 5 h 7 g 6 P S ST S T 0 ST c 011 ST 1 1 ST ST ST T 0 0 ST ST S a 0 T FIELD_0 1 Q ST ST T 0 Q S T 0 1 S T 0 1 0 4 0 0 4 5 0 5 7 0 4 4 1 4 3 1 5 5 1 6 6 e 4 y 0’ y 1’ y 2’ P Q T 0 d 5 h 7 g 6

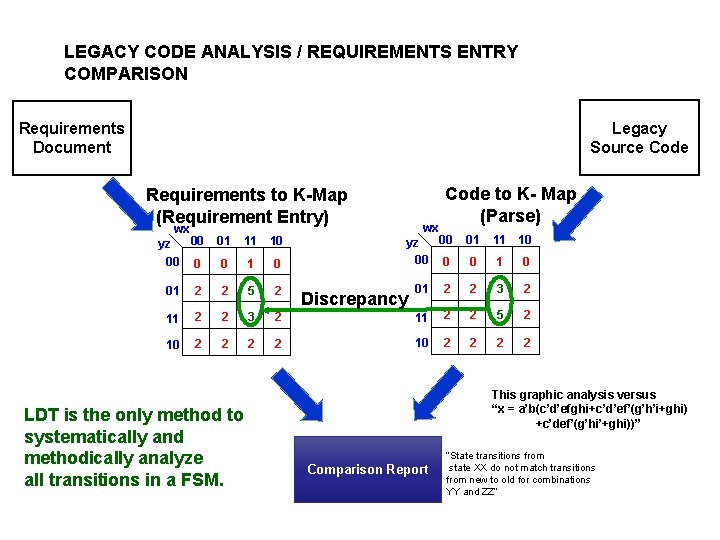
LEGACY CODE ANALYSIS / REQUIREMENTS ENTRY COMPARISON Legacy Source Code Requirements Document Requirements to K-Map (Requirement Entry) wx 00 yz 00 0 01 11 10 0 1 0 01 2 2 3 2 2 11 2 2 5 2 2 10 2 2 01 2 2 5 2 11 2 2 3 10 2 2 2 LDT is the only method to systematically and methodically analyze all transitions in a FSM. wx Code to K- Map (Parse) Discrepancy This graphic analysis versus “x = a’b(c’d’efghi+c’d’ef’(g’h’i+ghi) +c’def’(g’hi’+ghi))” Comparison Report “State transitions from state XX do not match transitions from new to old for combinations YY and ZZ“