The Logarithmic Function Lesson 4 3 Why What

The Logarithmic Function Lesson 4. 3

Why? • What happens when you enter into your calculator • If we want to know about limitations on the domain and range of the log function

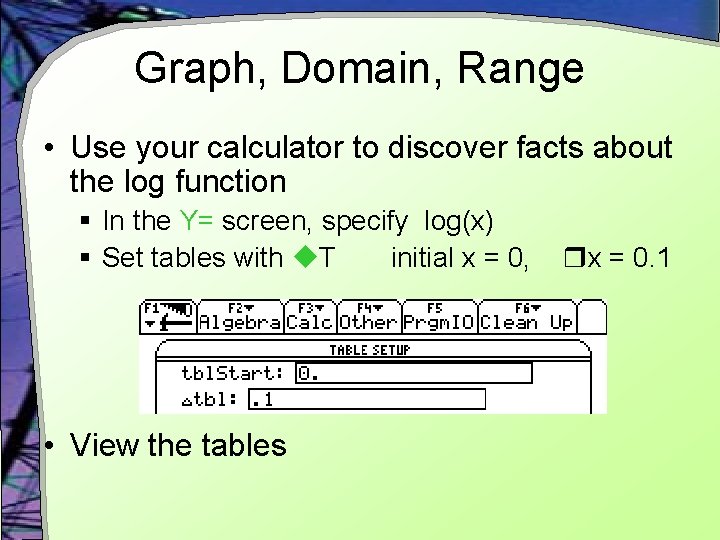
Graph, Domain, Range • Use your calculator to discover facts about the log function § In the Y= screen, specify log(x) § Set tables with T initial x = 0, • View the tables x = 0. 1

Graph, Domain, Range • Note domain for 0 < x < 1 • Change the x to 5, view again

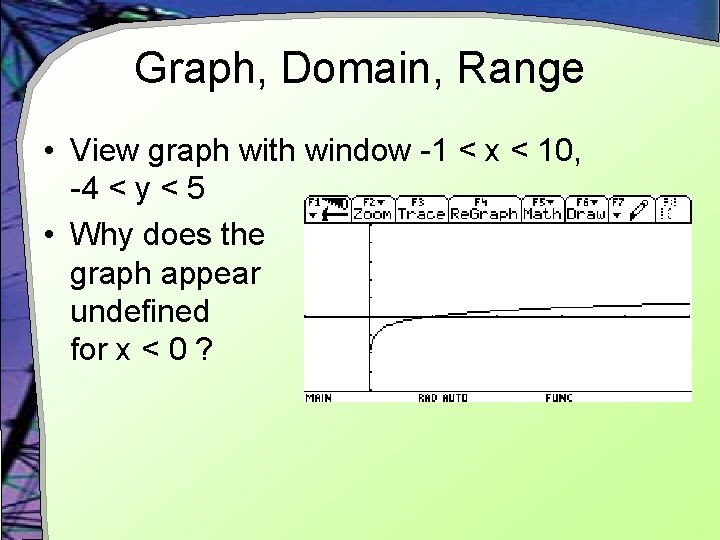
Graph, Domain, Range • View graph with window -1 < x < 10, -4 < y < 5 • Why does the graph appear undefined for x < 0 ?

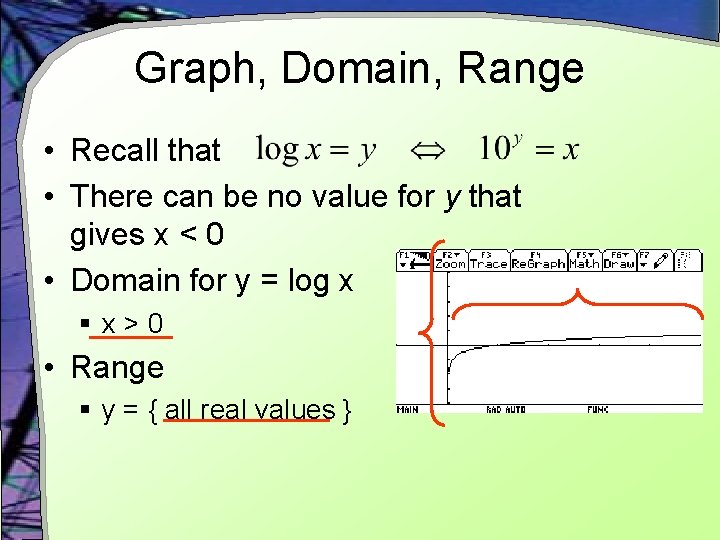
Graph, Domain, Range • Recall that • There can be no value for y that gives x < 0 • Domain for y = log x § x>0 • Range § y = { all real values }

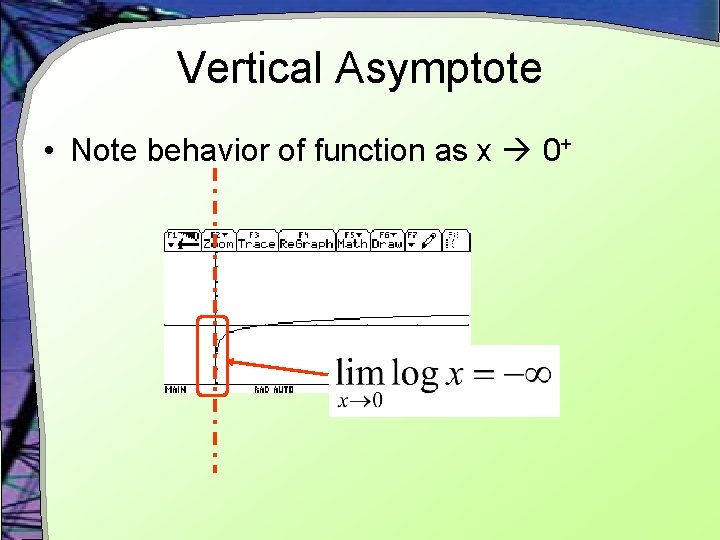
Vertical Asymptote • Note behavior of function as x 0+

Inverse Functions • Recall use of the Draw. Inv command on the graph screen You type in y 1(x)

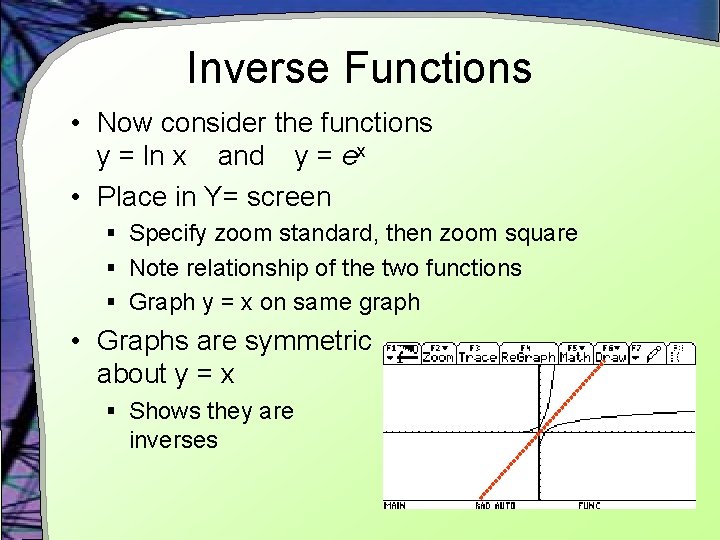
Inverse Functions • Now consider the functions y = ln x and y = ex • Place in Y= screen § Specify zoom standard, then zoom square § Note relationship of the two functions § Graph y = x on same graph • Graphs are symmetric about y = x § Shows they are inverses

Assignment • Lesson 4. 3 A • Page 173 • Exercises § 1 – 11 odd, 19 – 31 odd

Usefulness of Logarithms • Logarithms useful in measuring quantities which vary widely § Acidity (p. H) of a solution § Sound (decibels) § Earthquakes (Richter scale) Seismologists, Frank and Earnest

Chemical Acidity • p. H defined as p. H = -log[H+] § where [H+] is hydrogen ion concentration § measured in moles per liter • If seawater is [H+]= 1. 1*10 -8 § then –log(1. 1*10 -8) = 7. 96

Chemical Acidity • What would be the hydrogen ion concentration of vinegar with p. H = 3?

Logarithms and Orders of Magnitude • Consider increase of CDs on campus since 1990 § Suppose there were 1000 on campus in 1990 § Now there are 100, 000 on campus § The log of the ratio is the change in the order of magnitude

Logarithms and Orders of Magnitude • We use the log function because it “counts” the number of powers of 10 • This is necessary because of the vast range of some physical quantities we must measure § Sound intensity § Earthquake intensity

Decibels • Suppose I 0 is the softest sound the human ear can hear § measured in watts/cm 2 • And I is the watts/cm 2 of a given sound • Then the decibels of the sound is The log of the ratio

Decibels Approx. Decibel Level Example 0 Faintest sound heard by human ear. 30 Whisper, quiet library. 60 Normal conversation, sewing machine, typewriter. 90 Lawnmower, shop tools, truck traffic; 8 hours per day is the maximum exposure to protect 90% of people. 100 Chainsaw, pneumatic drill, snowmobile; 2 hours per day is the maximum exposure without protection. 115 Sandblasting, loud rock concert, auto horn; 15 minutes per day is the maximum exposure without protection. 140 Gun muzzle blast, jet engine; noise causes pain and even brief exposure injures unprotected ears. Maximum allowed noise with hearing protectors.

Decibels • If a sound doubles, how many units does its decibel rating increase? • Find out about hearing protection … § How many decibels does it reduce the sound § How much does that decrease the intensity of the sound?

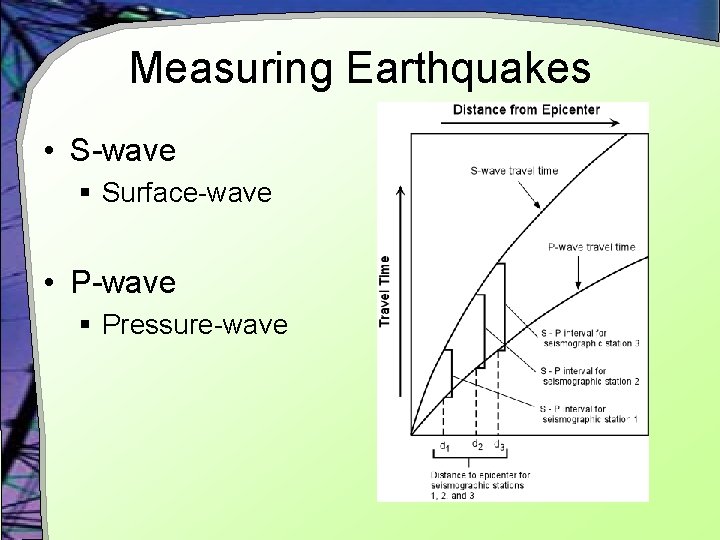
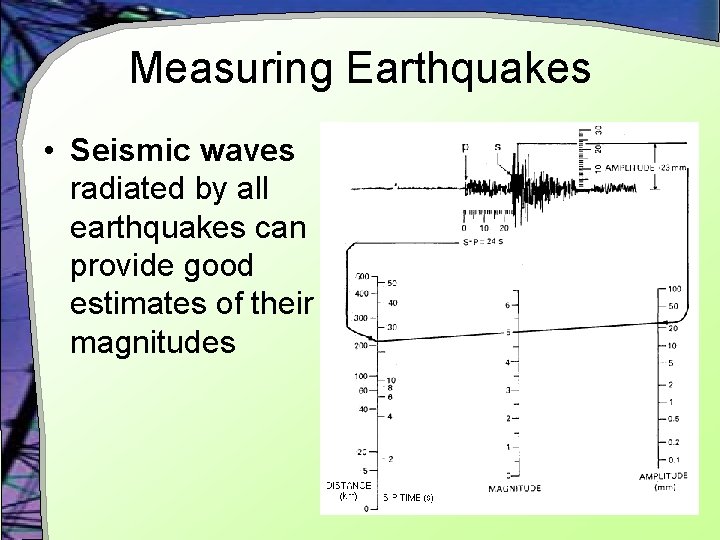
Measuring Earthquakes • S-wave § Surface-wave • P-wave § Pressure-wave

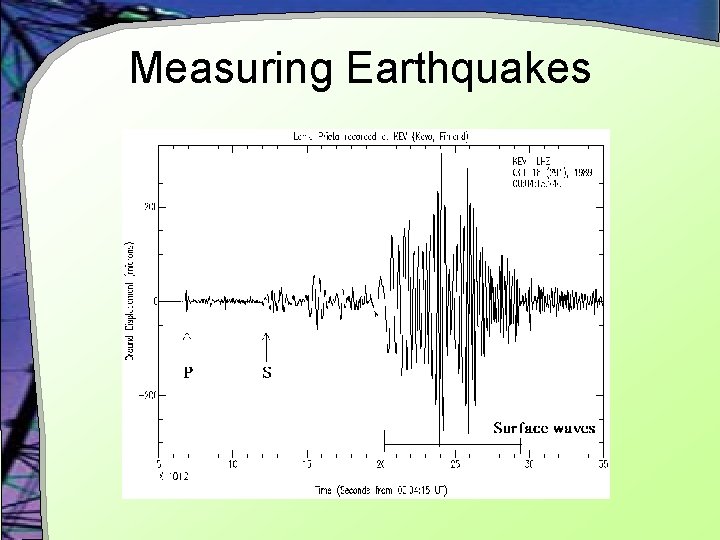
Measuring Earthquakes

Measuring Earthquakes • Seismic waves radiated by all earthquakes can provide good estimates of their magnitudes

Definition of Richter Scale • Magnitude of an earthquake with seismic waves of size W defined as • We measure a given earthquake relative to the strength of a "standard" earthquake

Comparable Magnitudes Richter Magnitude TNT for Seismic Energy Yield • • • • -1. 5 1. 0 1. 5 2. 0 2. 5 3. 0 3. 5 4. 0 4. 5 5. 0 5. 5 6. 0 6. 5 7. 0 6 30 320 1 4. 6 29 73 1, 000 5, 100 32, 000 80, 000 1 million 5 million 32 million • • • 7. 5 8. 0 8. 5 9. 0 10. 0 12. 0 160 million 1 billion 5 billion 32 billion 1 trillion 160 trillion ounces pounds tons tons tons tons tons Example (approximate) Breaking a rock on a lab table Large Blast at a Construction Site Large Quarry or Mine Blast Small Nuclear Weapon Average Tornado (total energy) Little Skull Mtn. , NV Quake, 1992 Double Spring Flat, NV Quake, 1994 Northridge, CA Quake, 1994 Hyogo-Ken Nanbu, Japan Quake, 1995; Largest Thermonuclear Weapon Landers, CA Quake, 1992 San Francisco, CA Quake, 1906 Anchorage, AK Quake, 1964 Chilean Quake, 1960 (San-Andreas type fault circling Earth) (Fault Earth in half through center, OR Earth's daily receipt of solar energy)

Assignment • Lesson 4. 3 B • Page 174 • Exercises § 13 – 17 all, 33 – 37 all