The Limits of Adiabatic Quantum Algorithms Alper Sarikaya

The Limits of Adiabatic Quantum Algorithms Alper Sarikaya Advised by Prof. Dave Bacon Computer Science & Engineering Chemistry University of Washington Undergraduate Research Symposium May 15, 2009 Quantum Computing Theory Group: http: //cs. washington. edu/homes/dabacon/qw/

Motivation • Transistors are getting smaller bits noisy bits • In 1994, Paul Shor showed that quantum algorithms have an exponential cm speed-up µm nm over their classical counterparts in factoring large prime numbers quantum bit pm

Quantum Computation • Qubit versus a classical bit. . where‘s the information stored? Deterministic Probabilistic 1 1 0. 6. 5 0. 4 0 0. 3 0 0. 5. 7 “Quantum” 1 -1 -1 • Adiabatically: take an incoming vector (input data), evolve the vector with an operator (a Hamiltonian); the answer is the smallest eigenvalue • Think linear algebra (Math 308)!

Simulating an Adiabatic Algorithm • Benefit of Quantum Algorithms: – Infinite precision analog computation can efficiently solve NP-complete problems • Adiabatic theorem - A physical system remains in its instantaneous eigenstate if a given perturbation is acting on it slowly enough and if there is a gap between the eigenvalue and the rest of the Hamiltonian's spectrum. - Max Born, Vladimir Fock (1928) • What is the benefit of building an adiabatic quantum computer? – Let’s compare the algorithm to a classical computer

• Testing efficiency hypothesis numerically: If the relationship between the eigenvalue gap and the number of qubits is negatively proportional, then an adiabatic quantum computer only offers a polynomial speedup over a classically-based counterpart. • To emulate a quantum computer classically, use the Markovian matrix as the operator in this study: where n is the number of qubits, β is varied between 0 and n, and the following two Hamiltonians are defined:

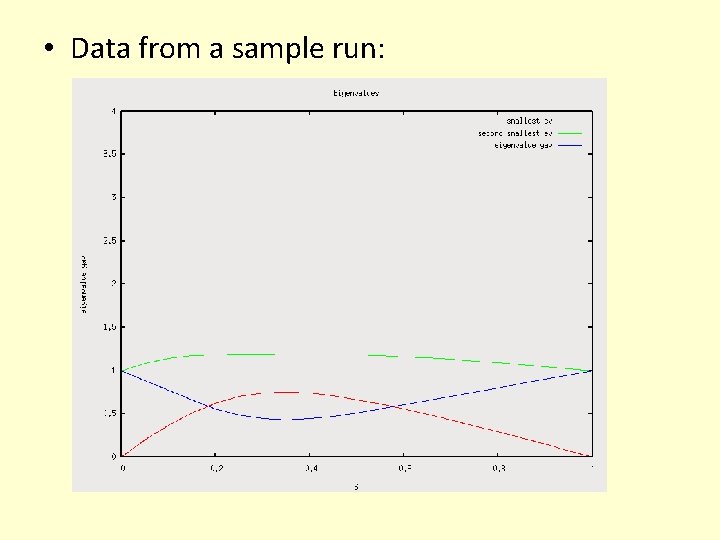
• Data from a sample run:

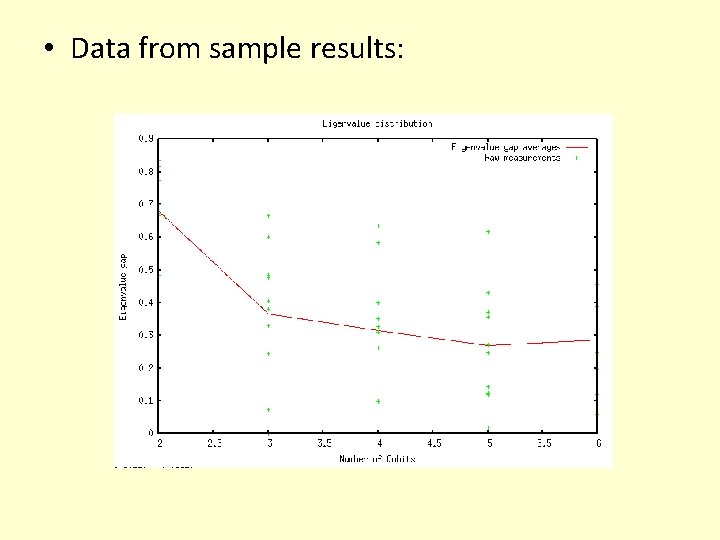
• Data from sample results:

Conclusions • There is indeed an inverse exponential relationship between the number of qubits and the smallest eigenvalue gap – Adiabatic quantum computers only offer a polynomial speedup! • This is only a numerical simulation of the hypothesis, not a proof

Future Directions • Move from numerical evidence in support of the hypothesis to a formal proof to conclusively uphold the efficiency concerns • Remember D-Wave? – Currently building an adiabatic quantum computer and gaining lots of capital from its promise – but it probably only offers a polynomial increase in efficiency!

Acknowledgments • Advisor: Professor Dave Bacon UW Computer Science & Engineering • Gregory Crosswhite UW Physics, Graduate Student • Quantum Computing Theory Group http: //cs. washington. edu/homes/dabacon/qw/ • This work supported in part by the National Science Foundation