The Limit of Polynomials Tomofumi Yuki INRIA Rennes

The Limit of Polynomials Tomofumi Yuki INRIA Rennes

Acknowledgements n Interesting discussions about polynomials n Paul Feautrier n Steven Derrien n Silviu-Ioan Filip n Year-Long Student Project n Adrien Chaffangeon n Adrien Gougeon n Timothee Anne IMPACT 2019 2

Limits of the Polyhedral Model n Strong framework for: n dependence analysis n program transformation n code generation n. . . n Strong limitation in exchange: n everything must be affine IMPACT 2019 3

Polynomial Extensions n Extend the class of functions (Feautrier 2015) n affine to polynomial n Lift restrictions of the polyhedral model: n polynomial scheduling n non-linear array accesses (e. g. , A[i*N+j]) n parametric tiling n + some work on code gen (IMPACT 2018) IMPACT 2019 4

Affine Scheduling n Ordering of operations n assign time stamps (affine functions) n model of loop transformations n dependences must be respected for (i = 1: N) for (j = 1: N) S 1(i, j); for (i = 1: N) S 2(i); Domain S 1: {i, j|1≤i≤N, 1≤j≤N} S 2: {i|1≤i≤N} for (i = 1: N) for (j = 1: N) S 1(i, j); S 2(i); Schedule sch 1(i, j) = (i, j) sch 2(i) = (i, N+1) IMPACT 2019 5

Farkas’ Lemma n Given polyhedral set D and affine function f is non-negative over D n iff f can be expressed as a linear combination of constraints defining D n Scheduling ≈ Positivity Check sch 1(op 1) > sch 2(op 2) f(op 1, op 2) > 0 n op 1 and op 2 are defined with polyhedral sets IMPACT 2019 6

Polynomial Scheduling n Handelman’s Theorem (simplified) n Given a polynomial f, and a set n f is strictly positive on D n iff it has the following representation Handelman Representation: linear combination of products of constraints IMPACT 2019 7

Two Research Questions n When do we need polynomial scheduling? n multi-dimensional affine is quite powerful Set Splitting? n static but. Index non-affine programs? n What are the implications of replacing Farkas’ Lemma with Handelman’s Theorem? non-negative / strictly positive n unbounded D / bounded D n No bound on degree of constraint products n IMPACT 2019 8

Implications for Scheduling n A class of polynomials does not have exact Handelman representation (Lasserre 2002) n Polynomial Scheduling Caveats: n a class of schedules is not explored n effectively acts as non-negativity certificate n constant matters Jean B. Lasserre. 2002. Semidefinite Programming vs. LP Relaxations for Polynomial Programming. Mathematics of Operations Research IMPACT 2019 9

Outline n Introduction n Farkas vs Handelman n Polynomial Optimization n Lasserre’s Results n Parametric Domains n Conclusion IMPACT 2019 10

Ex 1: Farkas’ Lemma n D: x∈[-1, 1] n x+1≥ 0 n 1 -x≥ 0 2 x+1 n Test if 2 x+1 is positive in D n Can 2 x+1 be expressed as n a(x+1)+b(1 -x)+c n where a, b, c≥ 0? 1 1 n No: 2 x+1 is not non-negative in D IMPACT 2019 11

Ex 2: Handelman’s Theorem n D: x∈[-1, 1] n x+1≥ 0 n 1 -x≥ 0 x 2+1 n Test if x 2+1 is positive in D n Consider degree 2 products: 1 [1, x+1, 1 -x, (x+1)2, (1 -x)2, (x+1)(1 -x)] 1 n Can x 2+1 be expressed with above? n Yes: (x+1)2+(1 -x)2 = 2 x 2+2 n 0. 5(x+1)2+0. 5(1 -x)2 = x 2+1 IMPACT 2019 12

Key Differences n The set D must be compact n not the case for Farkas’ Lemma n Potentially infinitely many terms n products of constraints introduce more terms n in practice: bound the degree (Σki) n Strict positivity n representation should give non-negativity IMPACT 2019 13

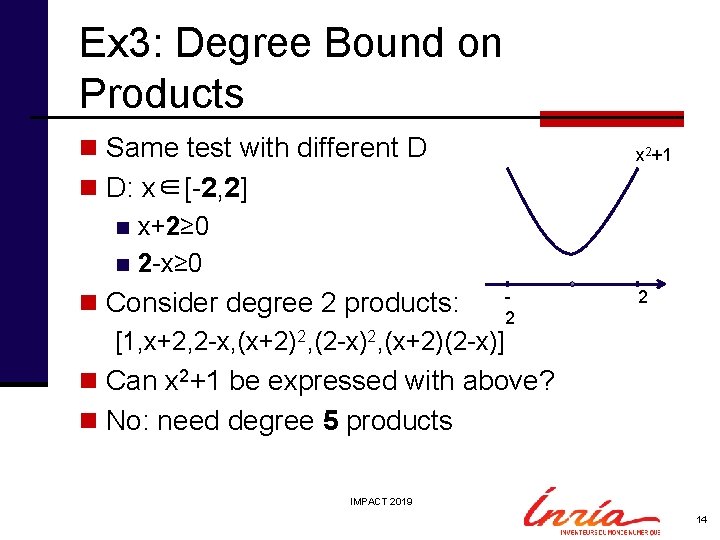
Ex 3: Degree Bound on Products n Same test with different D x 2+1 n D: x∈[-2, 2] n x+2≥ 0 n 2 -x≥ 0 n Consider degree 2 products: 2 [1, x+2, 2 -x, (x+2)2, (2 -x)2, (x+2)(2 -x)] 2 n Can x 2+1 be expressed with above? n No: need degree 5 products IMPACT 2019 14

Ex 4: Strict Positivity n Test for x 2 instead n D: x∈[-1, 1] n x+1≥ 0 n 1 -x≥ 0 x 2 n Consider degree 2 products: 1 [1, x+1, 1 -x, (x+1)2, (1 -x)2, (x+1)(1 -x)] 1 n Can x 2 be expressed with above? n No: you cannot express x 2 n even with high degree products IMPACT 2019 15

How is Scheduling Affected? n Polynomial Scheduling seems to “work” n but not the same as Farkas Scheduling n the impact of differences is unclear n Some answers from Polynomial Optimization n main results by Jean-Bernard Lasserre IMPACT 2019 16

Outline n Introduction n Farkas vs Handelman n Polynomial Optimization n Lasserre’s Results n Parametric Domains n Conclusion IMPACT 2019 17

Polynomial Optimization n Find the minimal value of a polynomial over a domain n links to positivity checks z 1 1 n Recall: positivity checks characterize positive functions over a domain IMPACT 2019 18

Ex 5: Finding the Minimum Value n D: x∈[-1, 1] x-x 2 n Find: min x-x 2 n Consider degree 2 products: 1 x+1 1 -x (x+1)2 (1 -x)2 (x+1)(1 -x) 1 1 IMPACT 2019 19

Ex 5: Finding the Minimum Value n D: x∈[-1, 1] x-x 2 n Find: min x-x 2 n Their linear combination: λ 0 + λ 1(x+1) + λ 2(1 -x) + λ 3(x+1)2 + λ 4(1 -x)2 + λ 5(x+1)(1 -x) 1 1 IMPACT 2019 20

Ex 5: Finding the Minimum Value n D: x∈[-1, 1] x-x 2 n Find: min x-x 2 n Expand the squares: λ 0 + λ 1(x+1) + λ 2(1 -x) + λ 3(x 2+2 x+1) + λ 4(x 2 -2 x+1) + λ 5(-x 2+1) 1 1 IMPACT 2019 21

Ex 5: Finding the Minimum Value n D: x∈[-1, 1] x-x 2 n Find: min x-x 2 1 n Factor by monomials: 1 (λ 0+λ 1+λ 2+λ 3+λ 4+λ 5) + x 2(λ 3+λ 4 -λ 5) min =1 + x (λ 1 -λ 2+2λ 3 -2λ 4) 1 =-1 λ 1=λ 5=1 x-x 2≥-2 IMPACT 2019 22

Ex 6: Finding the Minimum #2 n Find: min x 2 -x n Minimum is -0. 25 n Solution with different degrees: Degree 2 4 8 Solution -0. 5 -0. 333 -0. 286 16 32 -0. 267 -0. 258 1 1 fixed degree lower bound (relaxation to LP) NEVER reaches -0. 25!! IMPACT 2019 23

Lasserre’s Theorem n When exact solutions can be found n Theorem 3. 1 (Lasserre 2002) n M: bound on degree of constraint products n For a class of polynomials, solution to the relaxed problem approaches the exact solution as M→∞ (i. e. , never reached) n The class in question: n When a global minimizer is at the interior of D IMPACT 2019 24

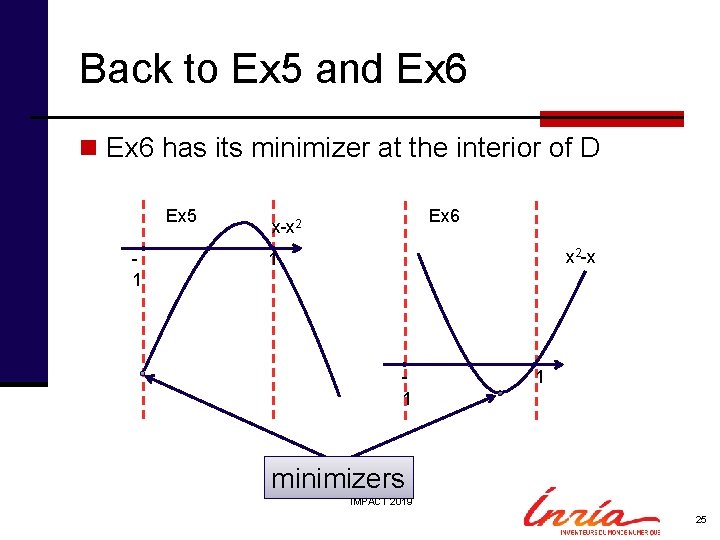
Back to Ex 5 and Ex 6 n Ex 6 has its minimizer at the interior of D Ex 5 1 Ex 6 x-x 2 x 2 -x 1 1 1 minimizers IMPACT 2019 25

What Does it Mean? n A class of polynomials cannot be found with polynomial scheduling n Example: x 2 for x∈[-1, 1] n x 2+1 needs M=2 n x 2+0. 25 needs M=5 n x 2 needs M=∞ x 2 n 1 1 n x 2 can never be found! n expressing x 2+c harder as c→ 0 IMPACT 2019 26

Relation to Strict Positivity n Lasserre’s Theorem shows when strict positivity in Handelman’s Theorem manifest n comes from M→∞ n The following are equivalent: Exact Solution to Polynomial Optimization Non-Negativity Certificate with Handelman n both require minimizers to be at the boundary IMPACT 2019 27

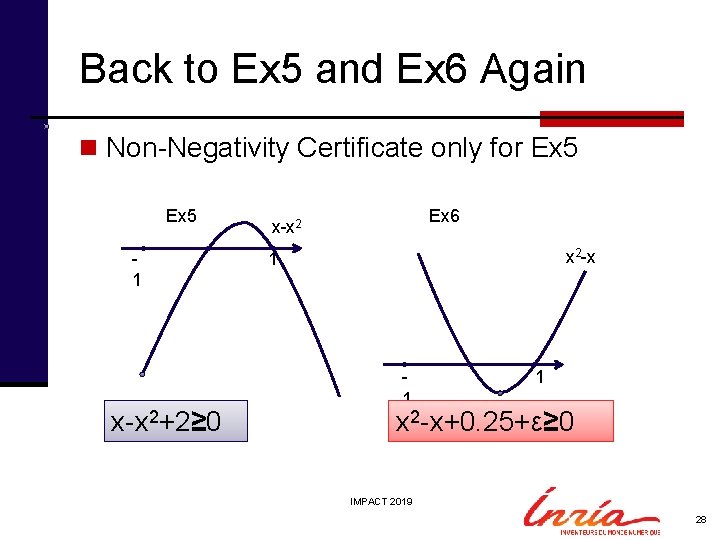
Back to Ex 5 and Ex 6 Again n Non-Negativity Certificate only for Ex 5 1 x-x 2+2≥ 0 Ex 6 x-x 2 x 2 -x 1 1 1 x 2 -x+0. 25+ε≥ 0 -x+0. 25>0 IMPACT 2019 28

What it Means for Scheduling n If Handelman Representation can be found with some M depends a lot on the polynomial n exploration space is sparse n Some are not expressible: n non-negative polynomials with global minimizer at interior n Constant Matters: n smaller constant need higher M IMPACT 2019 29

Optimization vs Scheduling n One subtle difference: n no constants in optimization context n Minimizer can be at the interior for scheduling x 2+1 1 1 x 2+1 found with M=2 x 2≥-1 is not exact LB of x 2 need “sufficiently high” M depending on the constant IMPACT 2019 30

Outline n Introduction n Farkas vs Handelman n Polynomial Optimization n Lasserre’s Results n Parametric Domains n Conclusion IMPACT 2019 31

On Parametric Domains n Everything so far: when set D is compact n matches hypotheses of Handelman’s Theorem n We use parametric domains all the time n usually not compact n Can we still use Handelman’s Theorem? IMPACT 2019 32

Problem with Parameters n D: x∈[-N, N]; Find: x 2+1 n family of D [-1, 1], [-2, 2], . . . n Every instance can be scaled to [-1, 1] x 2+0. 25 x 2+1 2 1 n Harder problem with higher values of N 2+1 for x∈[-N, N] n N→∞ x 2 for xx∈[-1, 1] No hope≈offinding IMPACT 2019 33

Parametric Solutions are Possible n D: x∈[-N, N]; Find: x 2+N 2 n All instances are equivalent: x 2+1 1 1 x 2+4 2 2 x 2+9 3 3 n x 2+N 2 can be found with M=2 n (x+N)2+(N-x)2 = 2 x 2+2 N 2 n solution for N=1 can be made parametric IMPACT 2019 34

Impact of Parameters n Further reduce the space of polynomials n the same linear combination must work for all parameter instances need monomials involving parameters n Example: x∈[-1, 1] x 2+1 x 2+0. 25 x 2 M 2 5 ∞ x∈[-N, N] x 2+N 2 x 2+0. 25 N 2 x 2 IMPACT 2019 35

Conclusion n Closer look into what it means to use Handelman’s Theorem for scheduling a good chunk of the space is excluded n especially with parameters n can be treated as non-negativity certificate n n Completely skipped ISS part! n led me to try and find polynomials with global minimizers at interior IMPACT 2019 36

Semi-Definite Programming? n SDP relxation n another approach to Polynomial Optimization n sum of squares instead of linear combination n Lasserre’s paper was about LP vs SDP n SDP is better! n Can we use SDP approach for scheduling? n seems promising n but compactness hypotheses remain IMPACT 2019 37

IMPACT 2019 38

Index-Set Splitting n Dependence Graph n no affine schedule n need PW-affine n Main reason: n affine function cannot change “direction” IMPACT 2019 39

Polynomial Guided ISS n Polynomials are multi-directional: j n e. g. , x 2 n Main idea: n first find a polynomial schedule n analyze polynomial n infer necessary pieces n Example: n (i-j)2 split at i=j i IMPACT 2019 40