The Law of Total Probability Let A 1

The Law of Total Probability Let A 1, A 2 and A 3 be three mutually exclusive and exhaustive events and let B denote some other event. Note for B to occur it has to be in conjunction with at least one of A 1, A 2 and A 3. Therefore, by applying the multiplication rule to a general situation of this type we obtain the following. The Law of Total Probability Let A 1, A 2, . . . , An be a set of mutually exclusive and exhaustive events. If B is any other event it follows that

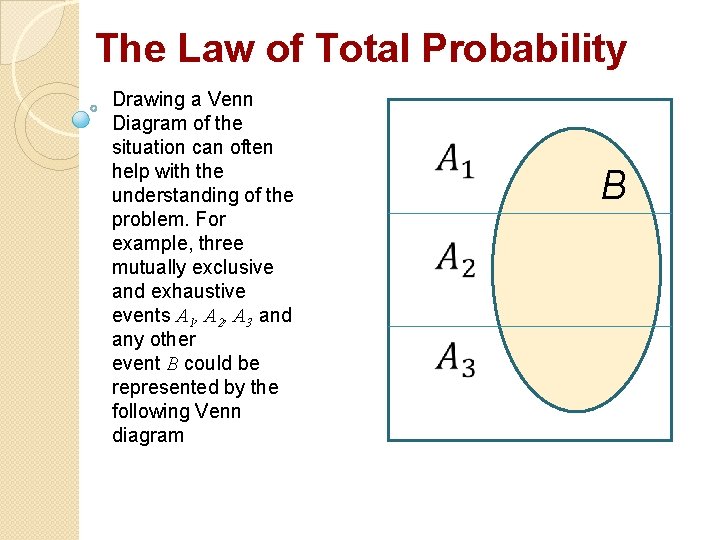
The Law of Total Probability Drawing a Venn Diagram of the situation can often help with the understanding of the problem. For example, three mutually exclusive and exhaustive events A 1, A 2, A 3 and any other event B could be represented by the following Venn diagram B

The Law of Total Probability Let A 1, A 2 and A 3 be three mutually exclusive and exhaustive events and let B denote some other event. Note for B to occur it has to be in conjunction with at least one of A 1, A 2 and A 3. Therefore, by applying the multiplication rule to a general situation of this type we obtain the following. The Law of Total Probability Let A 1, A 2, . . . , An be a set of mutually exclusive and exhaustive events. If B is any other event it follows that

The Law of Total Probability Example 1 There are three boxes, each containing a different number of light bulbs. The first box has 10 bulbs, of which four are dead, the second has six bulbs, of which one is dead, and the third box has eight bulbs of which three are dead. What is the probability of a dead bulb being selected when a bulb is chosen at random from one of the three boxes? Box 1 D Box 2 D Box 3 D

The Law of Total Probability Let A 1, A 2 and A 3 be three mutually exclusive and exhaustive events and let B denote some other event. Note for B to occur it has to be in conjunction with at least one of A 1, A 2 and A 3. Therefore, by applying the multiplication rule to a general situation of this type we obtain the following. The Law of Total Probability Let A 1, A 2, . . . , An be a set of mutually exclusive and exhaustive events. If B is any other event it follows that

The Law of Total Probability Example 2 Three boxes contain red and green balls. Box 1 has 5 red balls* and 5 green balls*, Box 2 has 7 red balls* and 3 green balls* and Box 3 contains 6 red balls* and 4 green balls*. The respective probabilities of choosing a box are 1/4, 1/6, 1/8. What is the probability that the ball chosen is green?

The Law of Total Probability Solution We begin by defining the following sets. Let, G = the ball chosen is green. B 1 = Box 1 is selected B 2 = Box 2 B 3 = Box 3 Then P(G|B 1) = 5/10, P(G|B 2) = 3/10 and P(G|B 3) = 4/10. Therefore, using the law of total probability we have

The Law of Total Probability Let A 1, A 2 and A 3 be three mutually exclusive and exhaustive events and let B denote some other event. Note for B to occur it has to be in conjunction with at least one of A 1, A 2 and A 3. Therefore, by applying the multiplication rule to a general situation of this type we obtain the following. The Law of Total Probability Let A 1, A 2, . . . , An be a set of mutually exclusive and exhaustive events. If B is any other event it follows that

The Law of Total Probability