The ladder problem And you Make a big

The ladder problem!!! And you Make a big fat drawing of this one to keep in your notes you wonderful students!!! As I also diagram the situation on the board

The problem: A ladder leaning on a FRICTIONLESS wall: Ladder mass = 15 kg Length of ladder is 10 m Θ = 60 O The main question to address here: What force of friction is required on the ground to stop the ladder from slipping? ? Θ

Ladder Forces • Identify all the forces acting on the ladder! + - F wall + FN F fr Fmgl -

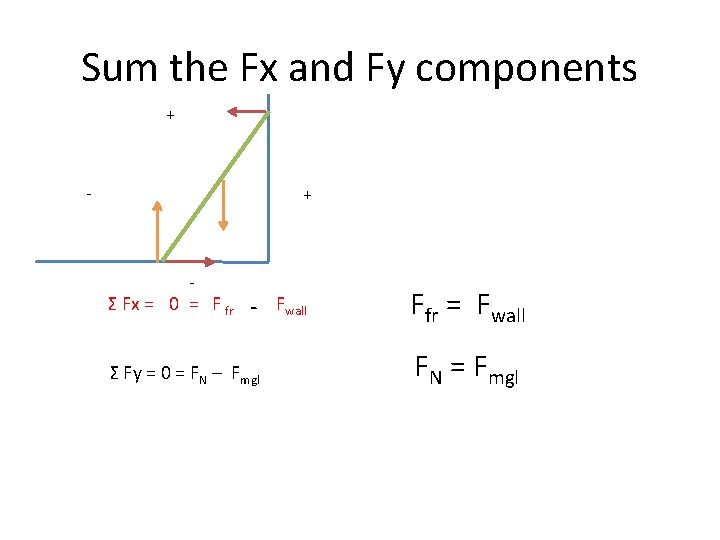
Sum the Fx and Fy components + - Σ Fx = 0 = F fr - Fwall Σ Fy = 0 = FN – Fmgl Ffr = Fwall FN = Fmgl

Consider TORQUE • Recall that the calculation of torque uses the forces perpendicular to the object that may rotate τ=F d where d is the distance to pivot • Since the ladder is not moving, the sum of the torques will be zero. Στ=0

If Ffr = Fwall • Then if we can calculate the Force of the wall, we can calculate the Force of friction needed to keep the ladder in place • We can calculate the force of the wall (and the force of friction) by looking at the torque relationships!!!!!

Calculate Torque ⏆wall = F⏊d = Fwall (cos 30) (10 m) ⏆ladder = F⏊d = Fmgl (cos 60) (5 m) Σ τ = 0 = τ wall – τ ladder so τ wall = τ ladder Fwall(cos 30)(10) = Fgl (cos 60) (5) Fwall(. 866) (10) = 15(9. 8) (. 5) (5) Fwall (8. 66) = 367. 5 Fwall = 42. 44 N The red arrows represent the perpendicular forces that are used in the calculation of torque.

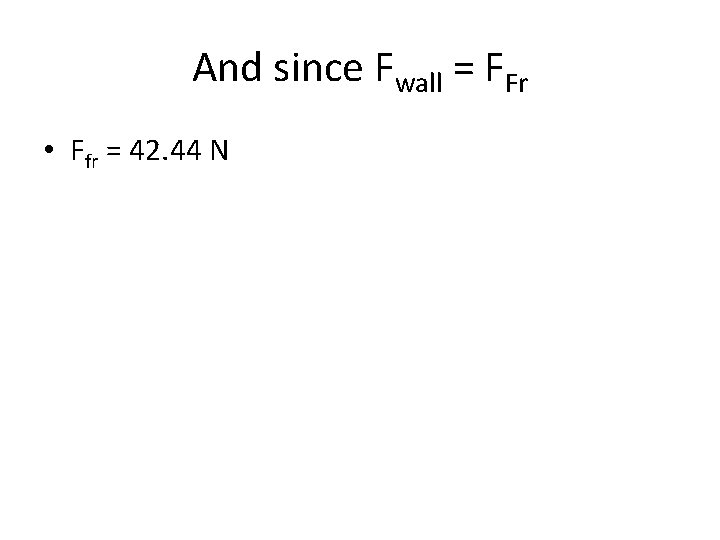
And since Fwall = FFr • Ffr = 42. 44 N

You try this one…. A ladder leaning on a FRICTIONLESS wall: Ladder mass = 25 kg Length of ladder is 7 m Θ = 40 O The main question to address here: What force of friction is required on the ground to stop the ladder from slipping? ?