The Kerr lens Transfer function of a lens

The Kerr lens Transfer function of a lens Spherical wave produced by a lens: Non-linear index: Plane wave Spherical wave In space: A better approach is to take the derivatives first: Identifying one gets:

The Kerr lens in time Depending in which order you proceed with an approximation, you could get different results. Example: calculation of the C element of an ABCD matrix, which is the second derivative in time of f. NL taken at the center of the pulse. 1) Approximate the Gaussian at the pulse center by a parabola, then take the second derivative: 1) Recognize there is no need for approximation. At t=0: and the C element is:

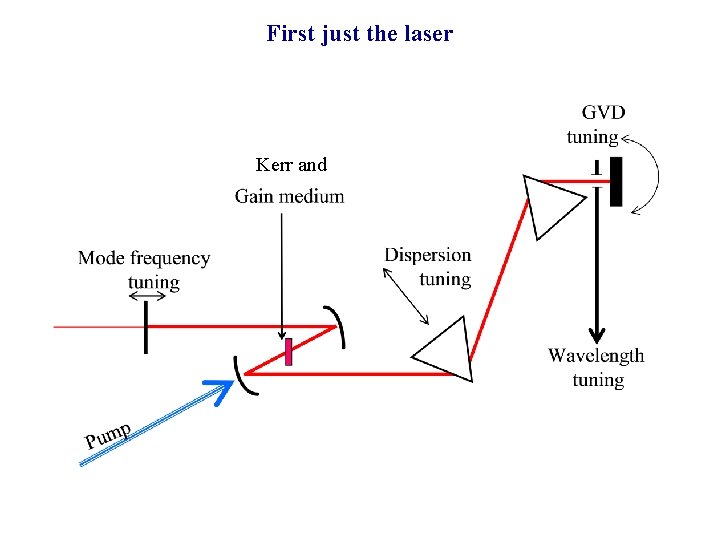
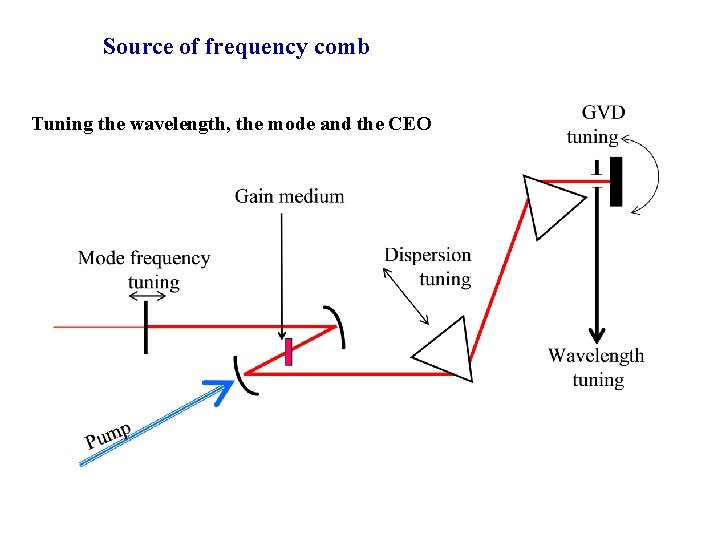
First just the laser Tuning the wavelength, the mode and the CEO Kerr and

Flashback: the temporal soliton Kerr effect and dispersion leads to the nonlinear Schroedinger equation The nonlinear Schroedinger equation leads to a soliton of order 1 The sech shaped pulse rattles back and forth in the cavity, producing a frequency comb First: just the laser how it produces cw, then a train of pulses or frequency comb Evolution of a single pulse in an ``ideal'' cavity How unequally spaced modes lead to a perfect frequency comb Amplitude modulation by Kerr lensing The frequency comb as seen by the experimentalist

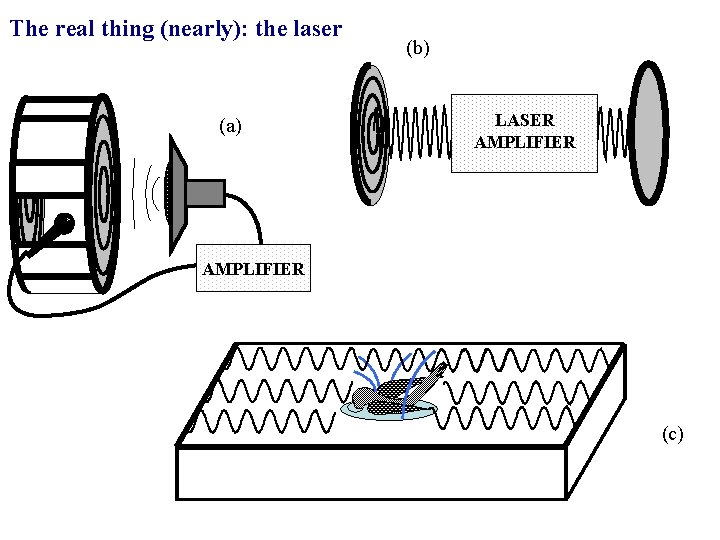
The real thing (nearly): the laser (a) (b) LASER AMPLIFIER (c)

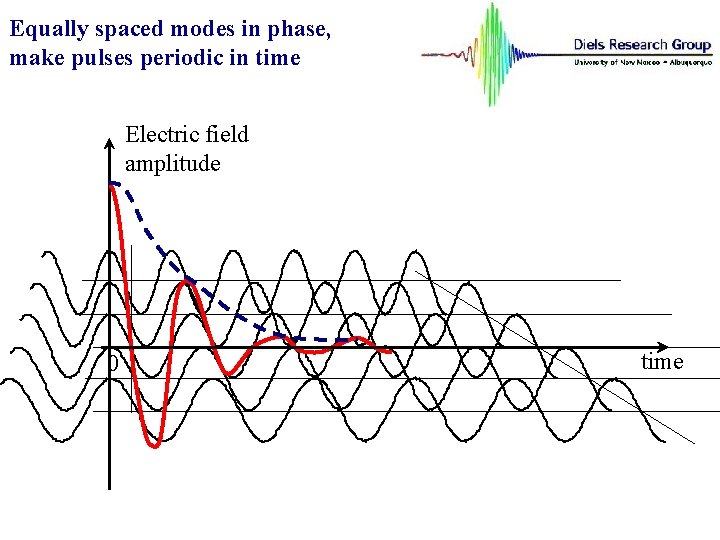
Equally spaced modes in phase, make pulses periodic in time Electric field amplitude 0 time

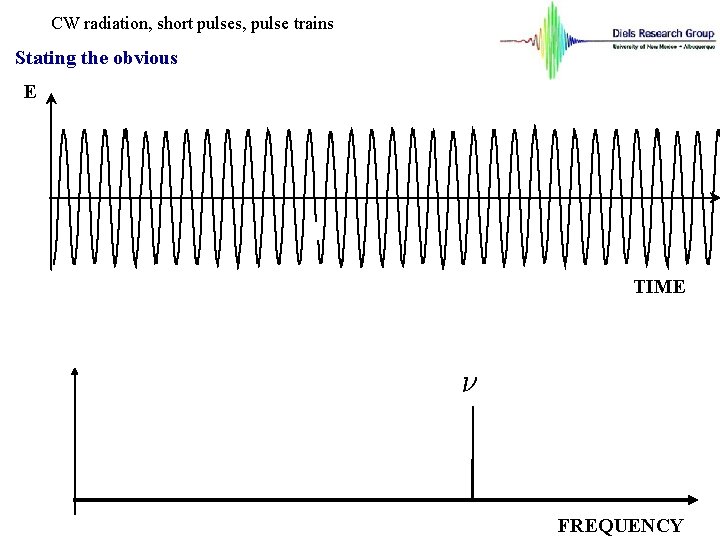
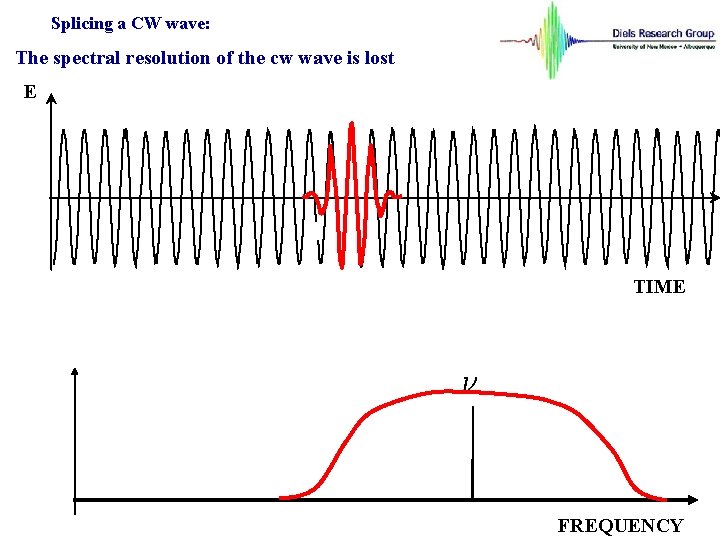
CW radiation, short pulses, pulse trains Stating the obvious E TIME FREQUENCY

Splicing a CW wave: The spectral resolution of the cw wave is lost E TIME FREQUENCY

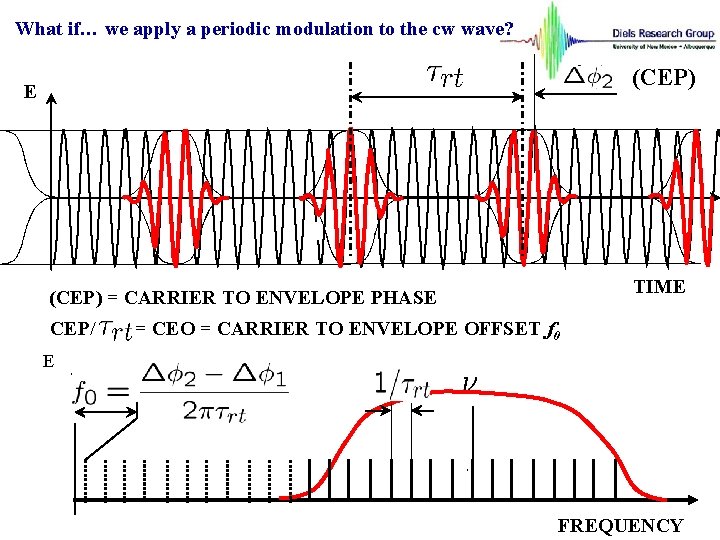
What if… we apply a periodic modulation to the cw wave? (CEP) E TIME (CEP) = CARRIER TO ENVELOPE PHASE CEP/ = CEO = CARRIER TO ENVELOPE OFFSET f 0 E FREQUENCY

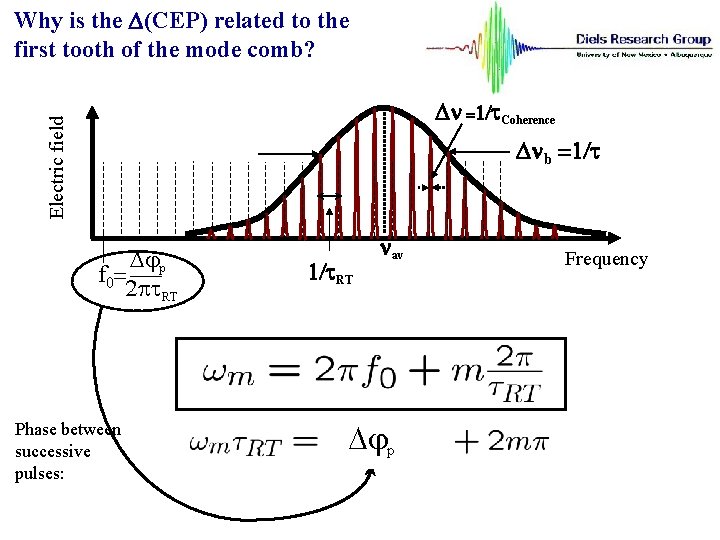
Why is the D(CEP) related to the first tooth of the mode comb? Electric field Dn =1/t. Coherence Dnb =1/t Djp f 0= 2 pt. RT Phase between successive pulses: 1/t. RT nav Djp Frequency

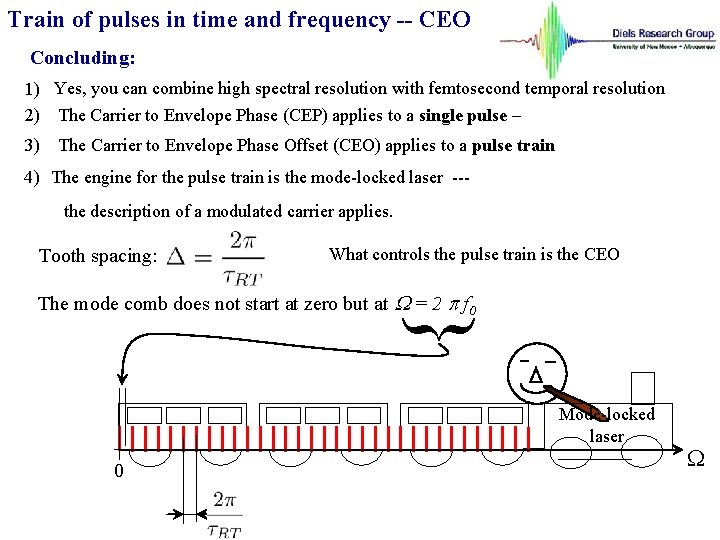
Train of pulses in time and frequency -- CEO Concluding: 1) Yes, you can combine high spectral resolution with femtosecond temporal resolution 2) The Carrier to Envelope Phase (CEP) applies to a single pulse – 3) The Carrier to Envelope Phase Offset (CEO) applies to a pulse train 4) The engine for the pulse train is the mode-locked laser --the description of a modulated carrier applies. Tooth spacing: What controls the pulse train is the CEO { The mode comb does not start at zero but at W = 2 p f 0 Mode-locked laser 0 W

Source of frequency comb Tuning the wavelength, the mode and the CEO

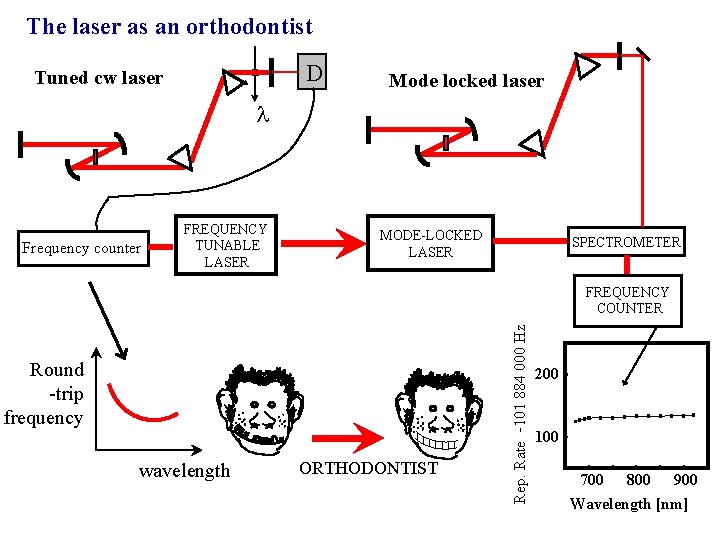
The laser as an orthodontist D Tuned cw laser Mode locked laser l Frequency counter FREQUENCY TUNABLE LASER MODE-LOCKED LASER SPECTROMETER Round -trip frequency wavelength ORTHODONTIST Rep. Rate - 101 884 000 Hz FREQUENCY COUNTER 200 100 700 800 900 Wavelength [nm]

Flashback: the temporal soliton Kerr effect and dispersion leads to the nonlinear Schroedinger equation The nonlinear Schroedinger equation leads to a soliton of order 1 The sech shaped pulse rattles back and forth in the cavity, producing a frequency comb First: just the laser how it produces cw, then a train of pulses or frequency comb Evolution of a single pulse in an ``ideal'' cavity How unequally spaced modes lead to a perfect frequency comb Amplitude modulation by Kerr lensing The frequency comb as seen by the experimentalist

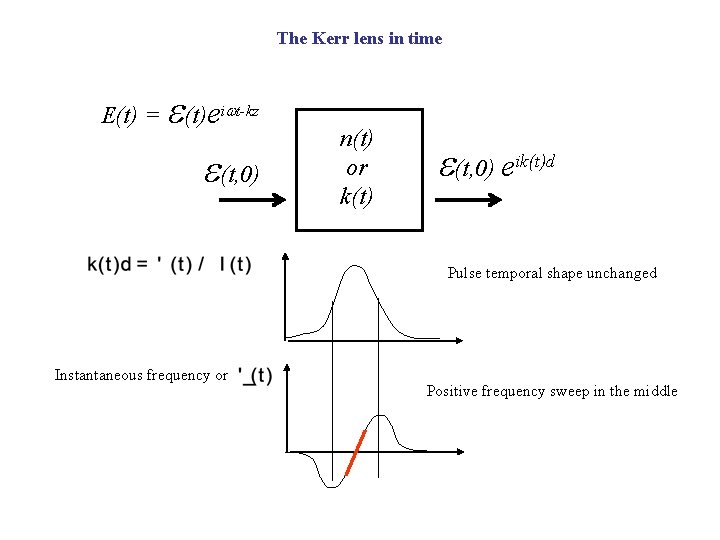
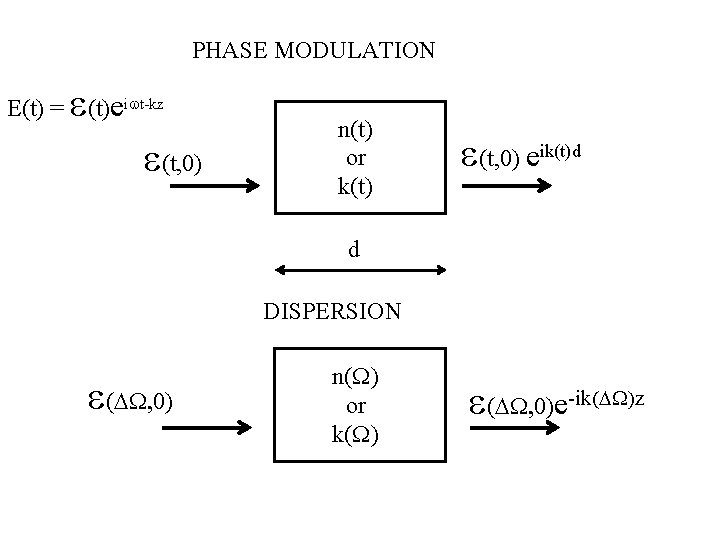
The Kerr lens in time e E(t) = (t)eiwt-kz e(t, 0) n(t) or k(t) e(t, 0) eik(t)d Pulse temporal shape unchanged Instantaneous frequency or Positive frequency sweep in the middle

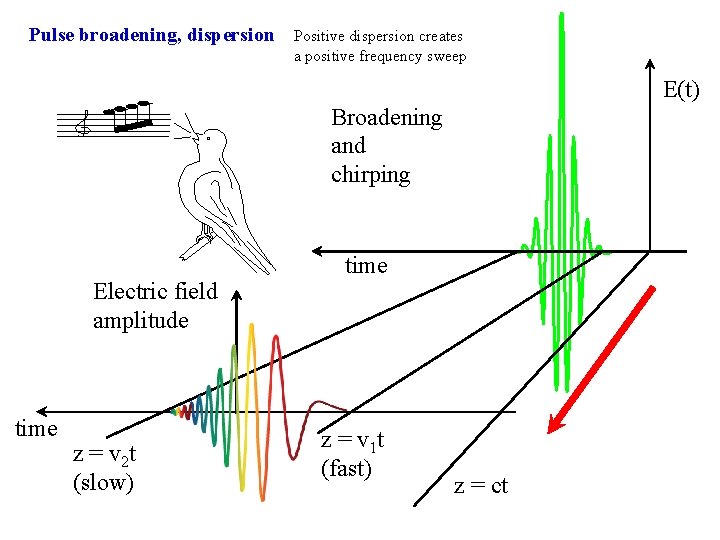
Pulse broadening, dispersion Positive dispersion creates a positive frequency sweep E(t) Broadening and chirping Electric field amplitude time z = v 2 t (slow) time z = v 1 t (fast) z = ct

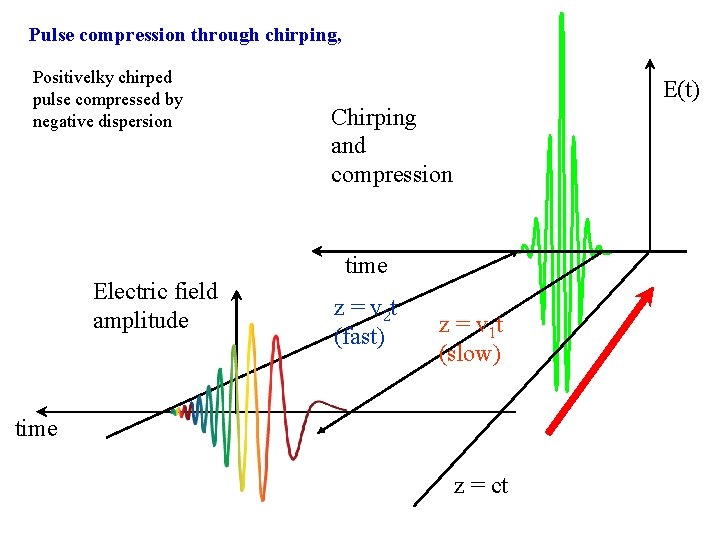
Pulse compression through chirping, Positivelky chirped pulse compressed by negative dispersion Electric field amplitude E(t) Chirping and compression time z = v 2 t (fast) z = v 1 t (slow) time z = ct

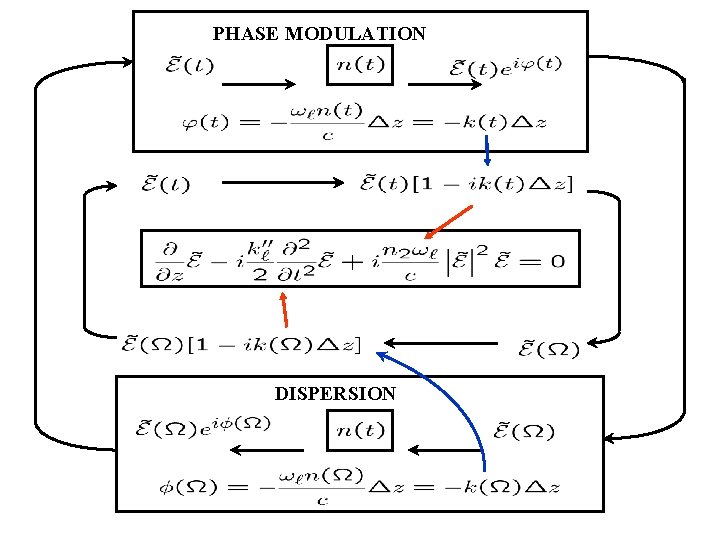
PHASE MODULATION e E(t) = (t)eiwt-kz e(t, 0) n(t) or k(t) e(t, 0) eik(t)d d DISPERSION e(DW, 0) n(W) or k(W) e(DW, 0)e-ik(DW)z

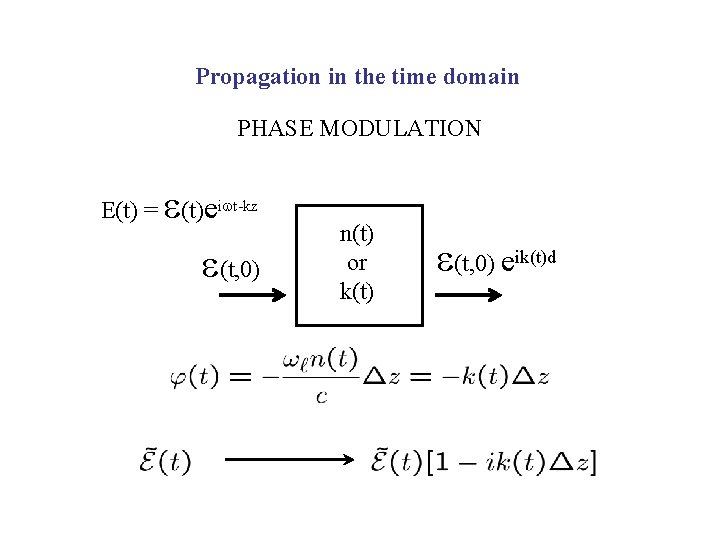
Propagation in the time domain PHASE MODULATION e E(t) = (t)eiwt-kz e(t, 0) n(t) or k(t) e(t, 0) eik(t)d

Propagation in the frequency domain DISPERSION e(DW, 0) n(W) or k(W) e(DW, 0)e-ik(DW)z Retarded frame and taking the inverse FT:

PHASE MODULATION DISPERSION

Equation in the retarded frame Characteristic field: Normalized distance: Solitons: solutions of the eigenvalue equation Characteristic time:

Why non-linear Schroedinger equation? Multiply by ]

Solution of the normalized NL Schroedinger equation The standard form is: Trial solution In these normalized units, there is an infinite family of solutions of ``order 1'', defined as the product of peak amplitude A by pulse duration ts being unity. But the correct “pulse area” is:

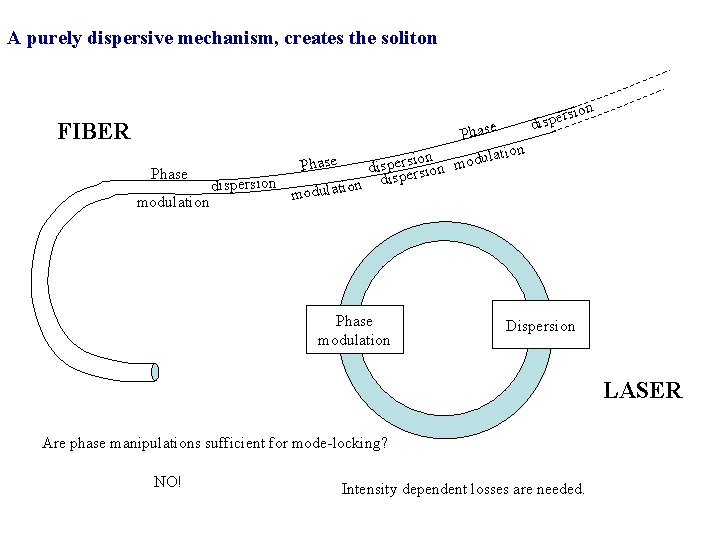
A purely dispersive mechanism, creates the soliton The soliton as a “canal wave” Recreation of the observation of John Russell for the 150 th anniversary of his observation in 1834.

Solution of the NL Schroedinger equation in physical units The leads to: which means that the soliton or order 1 corresponds to a balance between Kerr effect and dispersion. One can get to this relation between peak field, dispersion and nonlinear index by a simple “phase balancing act”.

Flashback: the temporal soliton Kerr effect and dispersion leads to the nonlinear Schroedinger equation The nonlinear Schroedinger equation leads to a soliton of order 1 The sech shaped pulse rattles back and forth in the cavity, producing a frequency comb First: just the laser how it produces cw, then a train of pulses or frequency comb Evolution of a single pulse in an ``ideal'' cavity How unequally spaced modes lead to a perfect frequency comb Amplitude modulation by Kerr lensing The frequency comb as seen by the experimentalist

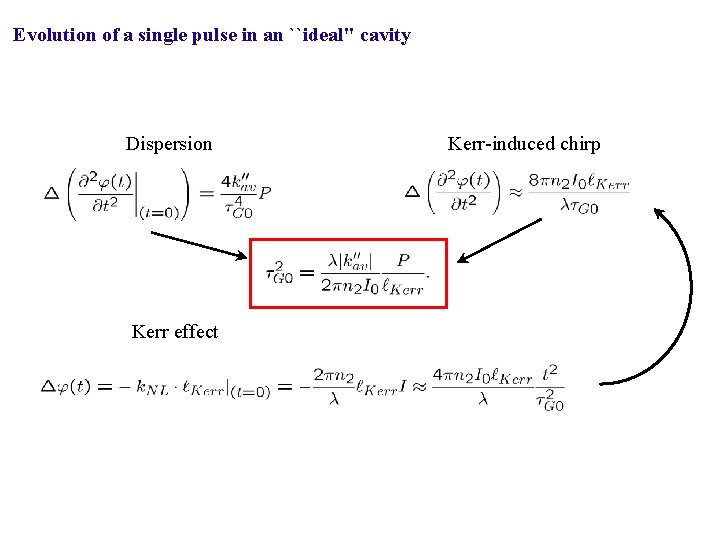
Evolution of a single pulse in an ``ideal'' cavity Dispersion Kerr effect Kerr-induced chirp

How unequally spaced modes lead to a perfect frequency comb Group delay Phase delay not equally spaced because nav = nav(w) Cavity modes: Unequally spaced modes, is contradictory to the fact that comb teeth are equally spaced. A cavity with ONLY Kerr modulation generates the pulse train: where F. T. where dispersion

Two related questions: As a pulse circulates in the cavity, does it evolve towards a steady state? Which mechanism makes the unequally spaced cavity modes Balance phase modulation by Kerr effect equidistant? and phase modulation by dispersion Evolution of a single pulse in an ``ideal'' cavity How unequally spaced modes lead to a perfect frequency comb SAME CONDITION

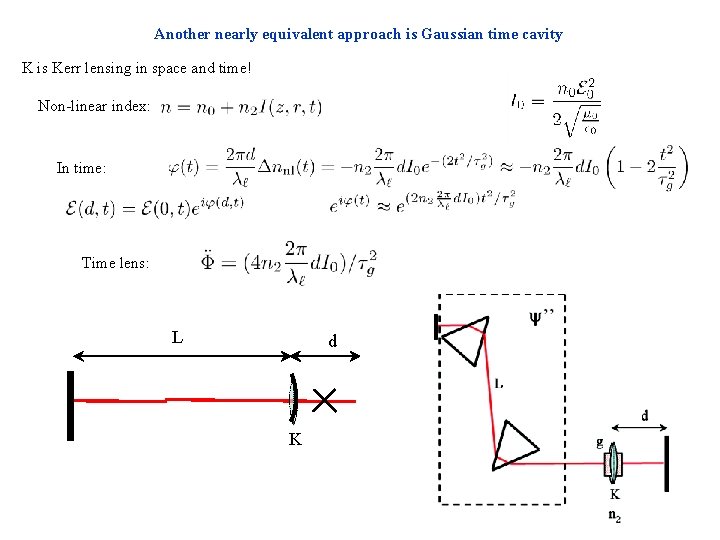
Another nearly equivalent approach is Gaussian time cavity K is Kerr lensing in space and time! Non-linear index: In time: Time lens: L d K

A purely dispersive mechanism, creates the soliton FIBER Phase tion a l n u o i d s e r s o a Ph dispe ersion m Phase disp n dispersion o i t a l u modulation Phase modulation r dispe sion Dispersion LASER Are phase manipulations sufficient for mode-locking? NO! Intensity dependent losses are needed.

Flashback: the temporal soliton Kerr effect and dispersion leads to the nonlinear Schroedinger equation The nonlinear Schroedinger equation leads to a soliton of order 1 The sech shaped pulse rattles back and forth in the cavity, producing a frequency comb First: just the laser how it produces cw, then a train of pulses or frequency comb Evolution of a single pulse in an ``ideal'' cavity How unequally spaced modes lead to a perfect frequency comb Amplitude modulation by Kerr lensing The frequency comb as seen by the experimentalist

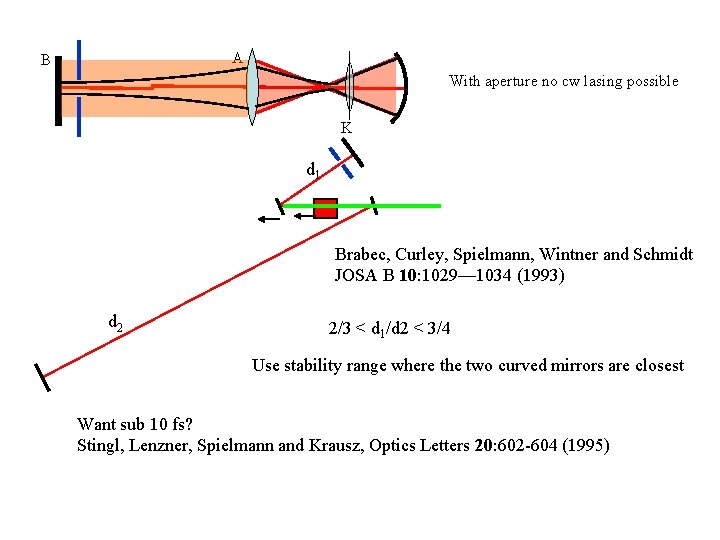
A B With aperture no cw lasing possible K d 1 Brabec, Curley, Spielmann, Wintner and Schmidt JOSA B 10: 1029— 1034 (1993) d 2 2/3 < d 1/d 2 < 3/4 Use stability range where the two curved mirrors are closest Want sub 10 fs? Stingl, Lenzner, Spielmann and Krausz, Optics Letters 20: 602 -604 (1995)

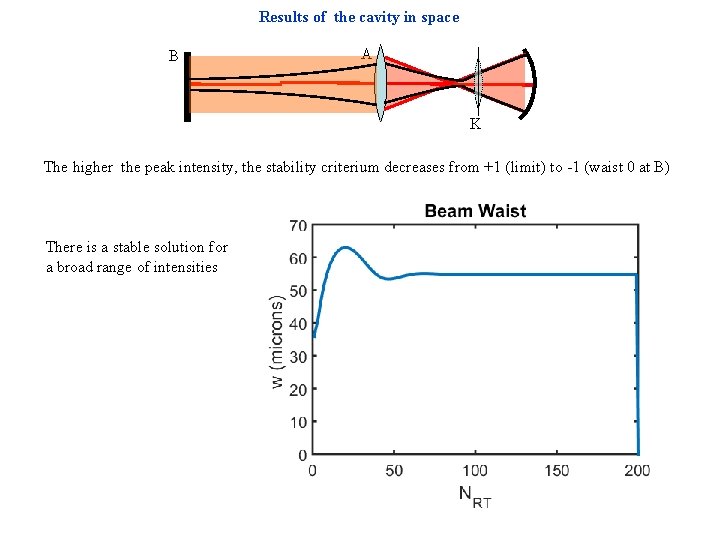
Results of the cavity in space B A K The higher the peak intensity, the stability criterium decreases from +1 (limit) to -1 (waist 0 at B) There is a stable solution for a broad range of intensities

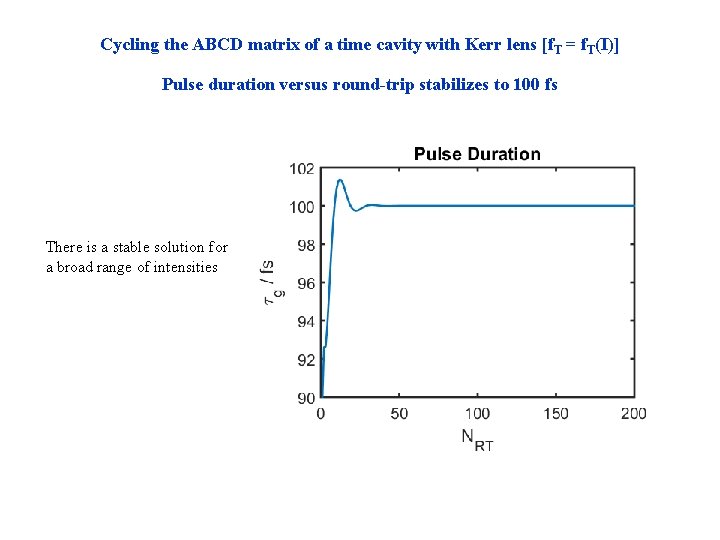
Cycling the ABCD matrix of a time cavity with Kerr lens [f. T = f. T(I)] Pulse duration versus round-trip stabilizes to 100 fs There is a stable solution for a broad range of intensities

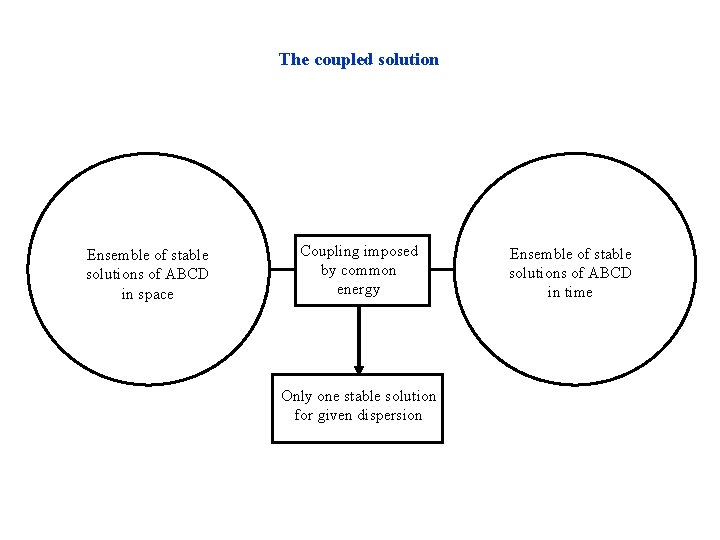
The coupled solution Ensemble of stable solutions of ABCD in space Coupling imposed by common energy Only one stable solution for given dispersion Ensemble of stable solutions of ABCD in time

Analogy of a pair of gyroscopes

Flashback: the temporal soliton Kerr effect and dispersion leads to the nonlinear Schroedinger equation The nonlinear Schroedinger equation leads to a soliton of order 1 The sech shaped pulse rattles back and forth in the cavity, producing a frequency comb First: just the laser how it produces cw, then a train of pulses or frequency comb Evolution of a single pulse in an ``ideal'' cavity How unequally spaced modes lead to a perfect frequency comb Amplitude modulation by Kerr lensing The frequency comb as seen by the experimentalist

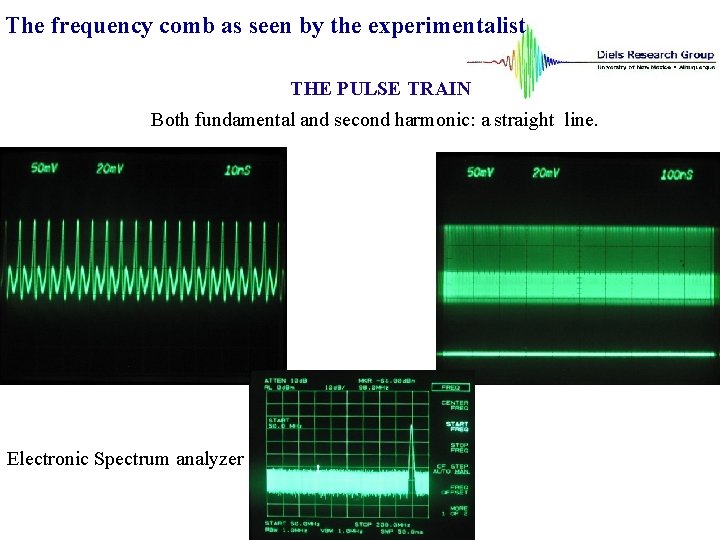
The frequency comb as seen by the experimentalist THE PULSE TRAIN Both fundamental and second harmonic: a straight line. Electronic Spectrum analyzer

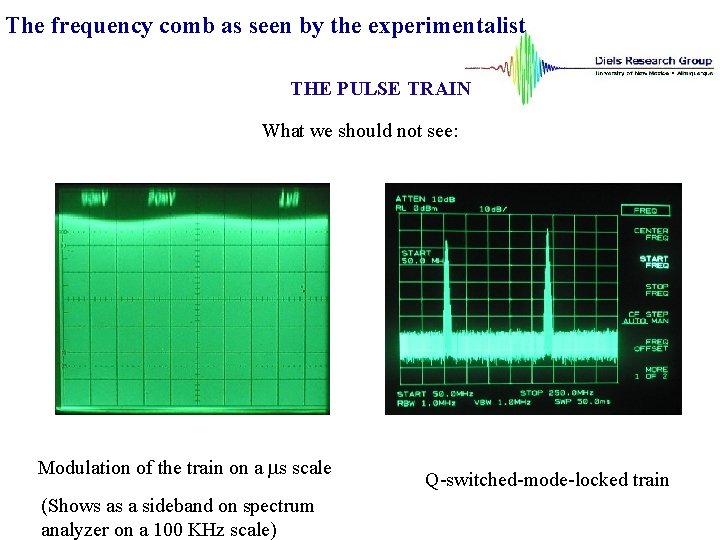
The frequency comb as seen by the experimentalist THE PULSE TRAIN What we should not see: Modulation of the train on a ms scale (Shows as a sideband on spectrum analyzer on a 100 KHz scale) Q-switched-mode-locked train

Concluding remarks The CEO is not a CEP! Carrier to Envelope Phase CEP property of a single ultrashort pulse Dimensionless! Carrier to Envelope Offset CEO property of a pulse train Dimension: frequency A CEO can be accurately measured, even when a CEP cannot be resolved