The Interval Constraint Solver For integer and real

The Interval Constraint Solver For integer and real variables

Outline ¡ ¡ ¡ Introduction & general overview Integer constraint solving Global constraints Reified constraints Real interval arithmetic Real constraint solving

Usage ¡ Load the interval constraint library by using : - lib(ic). at the beginning of your code, or type lib(ic). at the top-level ECLi. PSe prompt.

Functionality The IC library implements ¡ variables with integer or real domains ¡ basic equality, inequality and disequality constraints over linear and non-linear arithmetic expressions ¡ some “global” constraints for integer variables ¡ reified constraints ¡ search and optimisation facilities

Interval variables ¡ IC variables have a domain attached integer intervals : X{1. . 9} integer intervals with holes: Y{[2, 5. . 7]} real intervals: Z{-0. 5. . 3. 5} infinite intervals: 0. 5. . 1. 0 Inf} infinite integer intervals: 1. 0 Inf. . 3} W{V{-

Interval variables Vars : : Domain e. g. 1. . 9 X : : 1. . 9 Y Z W V 1. 0 Inf. . 3 ¡ ¡ : : : : [2, 5. . 7] -0. 5. . 3. 5 -0. 5. . 1. 0 Inf -1. 0 Inf. . 3 X #: : Y #: : [2, 5. . 7] Z $: : -0. 5. . 3. 5 W $: : -0. 5. . 1. 0 Inf V #: : - Attaches an initial domain to a variable or intersects its old domain with the new one. Type of bounds gives type of variable for : : (1. 0 Inf is considered type-neutral) ¡ ¡ #: : always imposes integrality $: : never imposes integrality

The basic set of constraints ¡ X #>= Y, Y #=< Z, X $>= Y, Y $=< Z Non-strict inequalities. ¡ X #> Y, Y #< Z, X $> Y, Y $< Z Strict inequalities. ¡ X #= Y, Y #= Z, X $= Y, Y $= Z Equality and disequality. ¡ X, Y, Z can be expressions + - * / ^ abs sqr exp ln sin cos min max sum. . . ¡ “#” constraints impose integrality, “$” constraints do not

Propagation behaviour ¡ Constraints are active: ? - [X, Y] : : 1. . 5, X #>= Y + 1. X = X{2. . 5}, Y = Y{1. . 4} Delayed goals: ic : (-(X{2. . 5}) + Y{1. . 4} =< -1) Yes ? - [X, Y] : : 1. . 5, X #>= Y + 1, Y #>= 3. X = X{[4, 5]}, Y = Y{[3, 4]} Delayed goals: ic : (-(X{[4, 5]}) + Y{[3, 4]} =< -1) Yes ? - [X, Y] : : 1. . 5, X #>= Y + 1, Y #>= 4. X = 5, Y = 4 Yes

Basic search support ¡ indomain(? Var) Instantiates Var to a value from its domain. Tries values from smallest to largest on backtracking. If X : : 1. . 3 then indomain(X) is the same as X=1 ; X=2 ; X=3 ¡ labeling(+Var. List) Invokes indomain/1 on each variable in the list. ¡ More sophisticated search covered in a later session

Exploring the search space ¡ Trying values from the domain ? - X : : 1. . 3. X = X{1. . 3} Yes ? - X : : 1. . 3, indomain(X). X = 1 More? (; ) X = 2 More? (; ) X = 3 Yes ? - X : : 1. . 2, Y : : 1. . 3, labeling([X, Y]). X = 1, Y = 1 More? (; ) X = 1, Y = 2 More? (; ) X = 1, Y = 3 More? (; ) X = 2, Y = 1 More? (; ) X = 2, Y = 2 More? (; ) X = 2, Y = 3 Yes

Standard example sendmore(Digits) : Digits = [S, E, N, D, M, O, R, Y], Digits : : 0. . 9, alldifferent(Digits), SEND + MORE = MONEY S #= 0, M #= 0, 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E #= 10000*M + 1000*O + 100*N + 10*E + Y, labeling(Digits).

Standard example ? - sendmore(Digits). Digits = [9, 5, 6, 7, 1, 0, 8, 2] More? (; ) No SEND 9567 MORE + 1085 = MONEY 10652

Other built-in constraints ¡ alldifferent(+List) All elements of the list are constrained to be pairwise different. ¡ integers(+List) All elements of the list are constrained to be integral. ¡ reals(+List) All elements of the list are constrained to be real. (Note this doesn’t mean they can’t also be integral: this is equivalent to List : : -1. 0 Inf. )

An arithmetic puzzle Is there a positive number which ¡ when divided by 3 gives a remainder of 1; ¡ when divided by 4 gives a remainder of 2; ¡ when divided by 5 gives a remainder of 3; and ¡ when divided by 6 gives a remainder of 4? model(X) X #> X #= (express the constraints with multiplications rather than divisions) : 0, A*3 B*4 C*5 D*6 + + 1, 2, 3, 4.

An arithmetic puzzle model(X) X #> X #= : 0, A*3 B*4 C*5 D*6 + + 1, 2, 3, 4. ? - model(X). X = X{58. . 1. 0 Inf} Delayed goals: ic: (-3*A{19. . 1. 0 Inf} + X{58. . 1. 0 Inf} =: = 1) ic: (-4*B{14. . 1. 0 Inf} + X{58. . 1. 0 Inf} =: = 2) ic: (-5*C{11. . 1. 0 Inf} + X{58. . 1. 0 Inf} =: = 3) ic: (X{58. . 1. 0 Inf} - 6*D{9. . 1. 0 Inf} =: = 4) Yes

An arithmetic puzzle ? - model(X). X = X{58. . 1. 0 Inf} Delayed goals: ic: (-3*A{19. . 1. 0 Inf} + X{58. . 1. 0 Inf} =: = 1) ic: (-4*B{14. . 1. 0 Inf} + X{58. . 1. 0 Inf} =: = 2) ic: (-5*C{11. . 1. 0 Inf} + X{58. . 1. 0 Inf} =: = 3) ic: (X{58. . 1. 0 Inf} - 6*D{9. . 1. 0 Inf} =: = 4) Yes ? - model(X), labeling([X]). X = 58 More? (; ) X = 118 More? (; ) X = 178 More? (; ). . .

N-ary constraints in lib(ic) ¡ S #= sum(List) Sum of N variables or sub-expressions. ¡ X #= min(List) Smallest of N variables or sub-expressions. ¡ X #= max(List) Largest of N variables or sub-expressions. ¡ alldifferent(List) All elements of the list are pairwise different.

Global constraints ¡ ¡ ¡ Constraints involving many variables Do more “global” reasoning Based on IC primitives : - lib(ic). ¡ Available in the libraries : : - lib(ic_global). lib(ic_cumulative). lib(ic_edge_finder 3).

Different constraint behaviours lib(ic) implementation of alldifferent/1 ? - [A, B, C]: : 1. . 3, D: : 1. . 5, ic: alldifferent([A, B, C, D]). A = A{1. . 3} B = B{1. . 3} C = C{1. . 3} D = D{1. . 5} Delayed goals: outof(A{1. . 3}, [], [B{1. . 3}, C{1. . 3}, D{1. . 5}]) outof(B{1. . 3}, [A{1. . 3}], [C{1. . 3}, D{1. . 5}]) outof(C{1. . 3}, [B{1. . 3}, A{1. . 3}], [D{1. . 5}]) outof(D{1. . 5}, [C{1. . 3}, B{1. . 3}, A{1. . 3}], []) Yes

Different constraint behaviours ¡ lib(ic_global) implementation ? - [A, B, C] : : 1. . 3, D: : 1. . 5, ic_global: alldifferent([A, B, C, D]). A = A{1. . 3} B = B{1. . 3} C = C{1. . 3} D = D{[4, 5]} Delayed goals: alldifferent([A{1. . 3}, B{1. . 3}, C{1. . 3}], 1) Yes

Why is it better? Primitive constraints see only e. g. A 1 2 3 4 5 D 1 2 3 4 5 #= ¡ Global view enables more reasoning: 1 A alldifferent B C D 2 3 4 5

More constraints in lib(ic_global) (I) alldifferent(+List, ++Capacity) declarative: No value in List occurs more than Capacity times. behaviour: Changes in the list variables affect other list variables. element(? Index, ++List, ? Value) declarative: The Index'th element of List is equal to Value. behaviour: Changes to either Index or Value may affect the other variable.

The element/3 constraint ¡ Defines a mapping from one variable to another: ? - element(I, [1, 3, 6, 3, 2], V). I = I{1. . 5} V = V{[1. . 3, 6]} Delayed goals: element(I{1. . 5}, [1, 3, 6, 3, 2], V{[1. . 3, 6]}) Yes ? - element(I, [1, 3, 6, 3, 2], V), V #= 3. I = I{[1, 3, 5]} V = V{[1, 2, 6]} Delayed goals: element(I{[1, 3, 5]}, [1, 3, 6, 3, 2], V{[1, 2, 6]}) Yes

More constraints in lib(ic_global) (II) ordered(++Rel, +List) declarative: List is an ordered list. behaviour: Changes in the list variables affect other list variables. ordered_sum(+List, ? Sum) declarative: List is an ordered list and the sum of its elements is Sum. behaviour: Changes in the list variables affect Sum and other list variables, and vice-versa. sorted(? List, ? Sorted. List) declarative: Sorted. List is a sorted permutation of List. behaviour: Change of bounds in one list may affect the other. sorted(? List, ? Sorted. List, ? Positions) declarative: Sorted. List is a sorted permutation of List, and Positions describes how the elements are permuted. behaviour: Change of bounds in any list may affect others.

Benefits of “global view” again ¡ Separate constraints for order and sum: ? - length(L, 3), L : : 0. . 20, ordered(=<, L), sum(L)#=10. L = [_1709{[0. . 10]}, _1722{[0. . 10]}, _1735{[0. . 10]}] ¡ Combined constraint: ? - length(L, 3), L : : 0. . 20, ordered_sum(L, 10). L = [_1694{[0. . 3]}, _1707{[0. . 5]}, _1720{[4. . 10]}] ¡ More inferences are possible! Remember that constraints operate locally

More constraints in lib(ic_global) (III) atmost(++N, +List, ++Value) declarative: At most N elements of List have value Value. behaviour: Changes in the list variables affect other list variables. occurrences(++Value, +List, ? N) declarative: Value occurs N times in List. behaviour: Changes in the list variables affect N and vice versa. lexico_le(+List 1, +List 2) declarative: List 1 is lexicographically less than or equal to List 2. behaviour: Change of bounds in one list may affect the other.

Scheduling constraints cumulative(+Starts, +Durations, +Resource. Usages, ++Resource. Limit) 4 3 3 2 4 1 cumulative([S 1, S 2, S 3, S 4], [1, 4, 2, 2], [1, 1, 3, 2], 4) 2 1 1 2 3 4 5 6. . . disjunctive(+Starts, +Durations) Same as cumulative(Starts, Durations, [1, . . . , 1], 1)

Scheduling constraints implementations ¡ The declarative constraints cumulative(+Starts, +Durations, +Resource. Usages, ++Resource. Limit) disjunctive(+Starts, +Durations) ¡ Three implementation variants lib(ic_cumulative) - linear algorithm on each change lib(ic_edge_finder) - quadratic algorithm lib(ic_edge_finder 3) - cubic algorithm ¡ More work, more propagation Edge-finder detects failures earlier Edge-finder gives more bound propagation

Reified constraints

Basic IC constraints revisited ¡ X #= Y #=(X, Y) #=(X, Y, B) ¡ #>=(X, Y) X #>= Y #>=(X, Y, B) ¡ X #< Y #<(X, Y) #<(X, Y, B) #=(X, Y) X #= Y etc. #=(X, Y, B) ¡ ¡ etc. Boolean variables B indicate truth of constraint

Reified constraints X #> Y X #= Y #>(X, Y, B) #=(X, Y, B) B=1 if the constraint is satisfied (entailed) ¡ B=0 if the constraint is false (disentailed) ¡ B{0. . 1} while unknown B can be set to ¡ 1 to enforce the constraint ¡ 0 to enforce its negation ¡

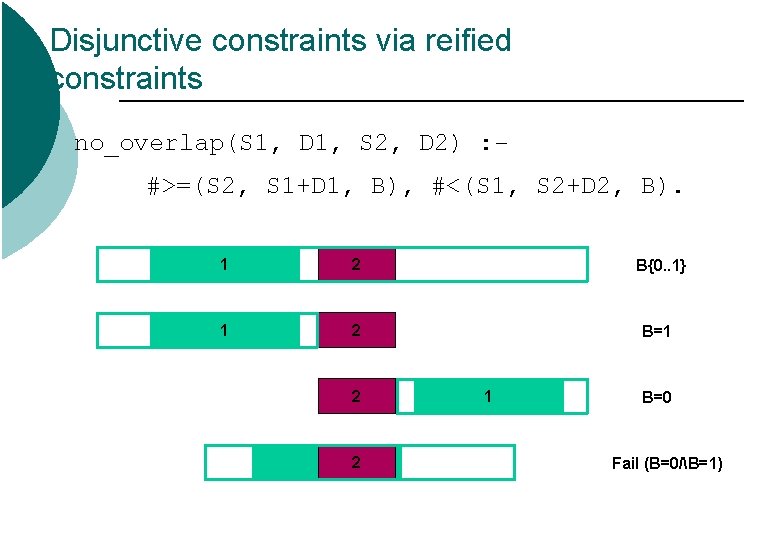
Disjunctive constraints via reified constraints no_overlap(S 1, D 1, S 2, D 2) : #>=(S 2, S 1+D 1, B), #<(S 1, S 2+D 2, B). 1 2 B{0. . 1} 1 2 B=1 2 1 B=0 Fail (B=0/B=1)

Constraint connectives ¡ neg C Negation of constraint C ¡ C 1 and C 2 ¡ C 1 or C 2 ¡ C 1 => C 2 C 1 implies C 2 E. g. X #= 0 => Y #> 0

Embedding reified constraints ¡ Constraints can appear in other expressions Evaluate to their reified boolean Sometimes the easiest way to reify a constraint ¡ B #= (X #>= Y + 2) ¡ 1 #= (X 1 #< Y 1 + (X 2 #=< Y 2)) ¡ This is how the constraint connectives (and, or, etc. ) are actually implemented

Disjunctive constraints via reified constraints (II) Note that the following are all equivalent: ¡ #>=(S 2, S 1+D 1, B), #<(S 1, S 2+D 2, B) ¡ (S 2 #>= S 1+D 1) #= (S 1 #< S 2+D 2) ¡ S 2 #>= S 1+D 1 or S 1 #>= S 2+D 2

Interval Arithmetic and Constraints

Interval Arithmetic Real values often can’t be represented exactly by floating point numbers ¡ Calculations introduce rounding errors Problems: ¡ Is the result really a solution? ¡ Were solutions missed? ¡

Interval Arithmetic Solution: ¡ Represent each real value by a pair of floating point bounds ¡ Arithmetic performed on intervals, with appropriate rounding ¡ A ground interval expresses that the exact real value lies somewhere between its bounds

Interval Arithmetic Two kinds of intervals: ¡ “Ground” interval Approximates a single (ground) real value Bounds never change ¡ “Variable” interval Approximates the domain of a real variable Bounds can be updated

Interval Arithmetic Problem: ¡ Arithmetic comparison now only partial ¡ E. g. is 0. 12__0. 16 = 0. 13__0. 15? > ? < ? Solution: ¡ Leave incomparable comparisons as delayed goals ¡ Presence of delayed goals indicates that the solution is a “candidate” only ¡ User decides if delayed goals indicate a problem

The bounded real data type ¡ ¡ Written lwb__upb, where lwb and upb are the lower and upper floating point bounds, respectively (e. g. 0. 12__0. 16) Not usually entered directly: normally occur as result of computation ¡ breal/1 tests whether a term is a bounded real ¡ breal/2 converts other numeric types to bounded reals ¡ breal_min/2, breal_max/2 and breal_bounds/3 can be used to obtain the floating point bounds of a bounded real

The bounded real data type ? - X is sqrt(breal(2)). X = 1. 4142135623730949__1. 4142135623730954 Yes ? - Y is float(1) / 10, X is Y + Y + Y + Y. X = 0. 9999999989 Y = 0. 1 Yes ? - Y is breal(1) / 10, X is Y + Y + Y + Y. X = 0. 9999999911__1. 000000009 Y = 0. 0999999992__0. 1000000002 Yes

Working with Bounded Reals ¡ Take care with arithmetic comparisons if arguments might be bounded reals E. g. X > 0, X =: = 0, etc. will leave delayed goals behind if X spans 0 ¡ Decide what should happen and design tests appropriately E. g. X > 0, not X =< 0, and not X > 0 are equivalent for most numeric types, but do different things for bounded reals

IC for real variables ¡ IC’s general constraints ($=/2, $=</2, etc. ) work for: real variables integer variables a mix of both ¡ ¡ Propagation is performed using safe arithmetic Integrality preserved where possible

Propagation behaviour (I) ¡ For integers, just like integer constraints: ? - [X, Y] : : 1. . 5, X $>= Y + 1. X = X{2. . 5}, Y = Y{1. . 4} Delayed goals: ic : (-(X{2. . 5}) + Y{1. . 4} =< -1) Yes ? - [X, Y] : : 1. . 5, X $>= Y + 1, Y $>= 3. X = X{[4, 5]}, Y = Y{[3, 4]} Delayed goals: ic : (-(X{[4, 5]}) + Y{[3, 4]} =< -1) Yes ? - [X, Y] : : 1. . 5, X $>= Y + 1, Y $>= 4. X = 5, Y = 4 Yes

Propagation behaviour (II) ¡ For reals, uses safe arithmetic: ? - [X, Y] : : 1. 0. . 5. 0, X $>= Y + 1. X = X{1. 999999998. . 5. 0} Y = Y{1. 0. . 4. 000000009} Delayed goals: ic : (-(X{1. 999999998. . 5. 0}) + Y{1. 0. . 4. 000000009} =< -1) Yes ? - [X, Y] : : 1. 0. . 5. 0, X $>= Y + 1, Y $>= 3. X = X{3. 999999996. . 5. 0} Y = Y{3. 0. . 4. 000000009} Delayed goals: ic : (-(X{3. 999999996. . 5. 0}) + Y{3. 0. . 4. 000000009} =< -1) Yes

Propagation behaviour (III) ¡ Variables don’t usually end up ground: ? - [X, Y] : : 1. 0. . 5. 0, X $>= Y + 1, Y $>= 4. X = X{4. 999999991. . 5. 0} Y = Y{4. 0. . 4. 000000009} Delayed goals: ic : (-(X{4. 999999991. . 5. 0}) + Y{4. 0. . 4. 000000009} =< -1 Yes

Solving real constraints ¡ IC provides two methods for solving real constraints ¡ locate/2, 3 good when there a finite number of discrete solutions Works by splitting domains ¡ squash/3 good for refining bounds on a continuous feasible region Works by trying to prove parts of domains infeasible

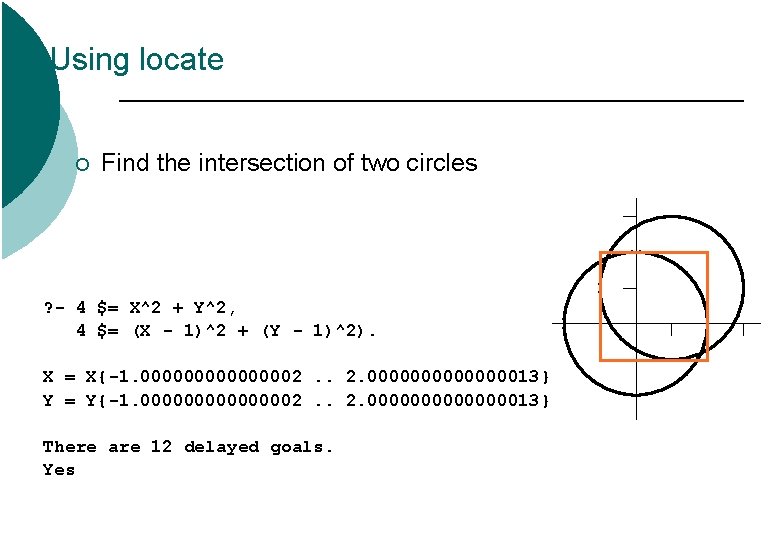
Using locate ¡ Find the intersection of two circles ? - 4 $= X^2 + Y^2, 4 $= (X - 1)^2 + (Y - 1)^2). X = X{-1. 00000002. . 2. 000000013} Y = Y{-1. 00000002. . 2. 000000013} There are 12 delayed goals. Yes

Using locate ? - 4 $= X^2 + Y^2, 4 $= (X - 1)^2 + (Y – 1)^2, locate([X, Y], 1 e-5). X = X{-0. 82287566035527082. . -0. 822875644848199} Y = Y{1. 8228756448481993. . 1. 8228756603552705} There are 12 delayed goals. More ? ; X = X{1. 8228756448481993. . 1. 8228756603552705} Y = Y{-0. 82287566035527082. . -0. 822875644848199} There are 12 delayed goals. Yes

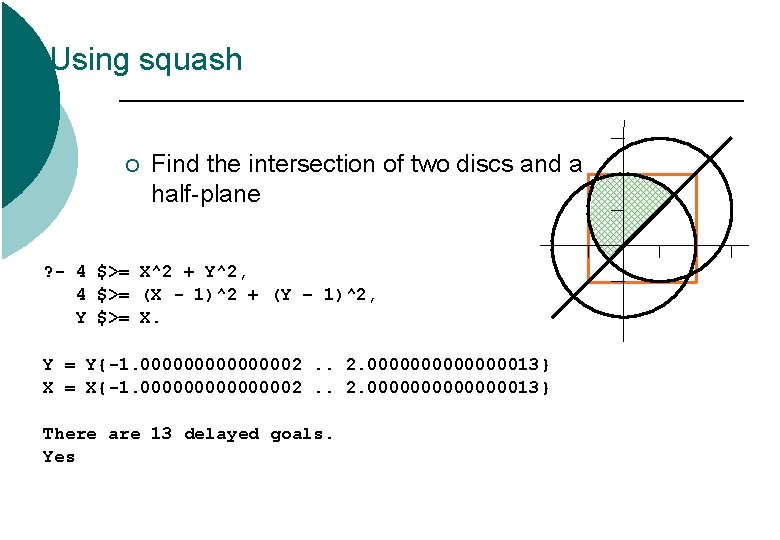
Using squash ¡ Find the intersection of two discs and a half-plane ? - 4 $>= X^2 + Y^2, 4 $>= (X - 1)^2 + (Y – 1)^2, Y $>= X. Y = Y{-1. 00000002. . 2. 000000013} X = X{-1. 00000002. . 2. 000000013} There are 13 delayed goals. Yes

Using squash ? - 4 $>= X^2 + Y^2, 4 $>= (X - 1)^2 + (Y – 1)^2, Y $>= X, squash([X, Y], 1 e-5, lin). X = X{-1. 00000002. . 1. 4142135999632603} Y = Y{-0. 41421359996326107. . 2. 000000013} There are 13 delayed goals. Yes

IC Example (modelling, abstraction) George is contemplating buying a farm which is a very strange shape, comprising a large triangular lake with a square field on each side. ¡ ¡ The area of the lake is exactly seven acres. The area of each field is an exact whole number of acres. What is the smallest possible total area of the three fields? C 7 A B

IC Example - Model farm(F, A, B, C) : [A, B, C] : : 0. 0. . 1. 0 Inf, triangle_area(A, B, C, 7), [F, FA, FB, FC] : : 1. 0 Inf, integral square_area(A, FA), square_area(B, FB), square_area(C, FC), F #= FA+FB+FC, % The 3 sides of the lake % The lake area is 7 % The square areas are C 7 A % Avoid symmetric solutions FA $>= FB, FB $>= FC. B

IC Example - Abstraction triangle_area(A, B, C, Area) : S $>= 0, S $= (A+B+C)/2, Area $= sqrt(S*(S-A)*(S-B)*(S-C)). square_area(A, Area) : Area $= sqr(A). C 7 A B

IC Example - Search solve(F, A, B, C) : farm(F, A, B, C), % the model indomain(F), % ensure that solution is minimal locate([A, B, C], 0. 01). ? - solve(F, A, B, C). F = 50 A = A{4. 4721359549995787. . 4. 4721359549995805} B = B{4. 12310562561766. . 4. 1231056256176615} C = C{3. 6055512754639887. . 3. 6055512754639896} There are 23 delayed goals. More? C 7 A B

Exercises ¡ ¡ Try the SEND+MORE=MONEY problem for yourself Try the exercises from “Getting Started with Interval Constraints” in the tutorial manual (section 8. 9 in my copy, on page 84 (+10)) Try the first search exercise Look at “Working with Real Numbers and Variables” (chapter 9) in the tutorial manual