The International System of Units Quantity Unit Name

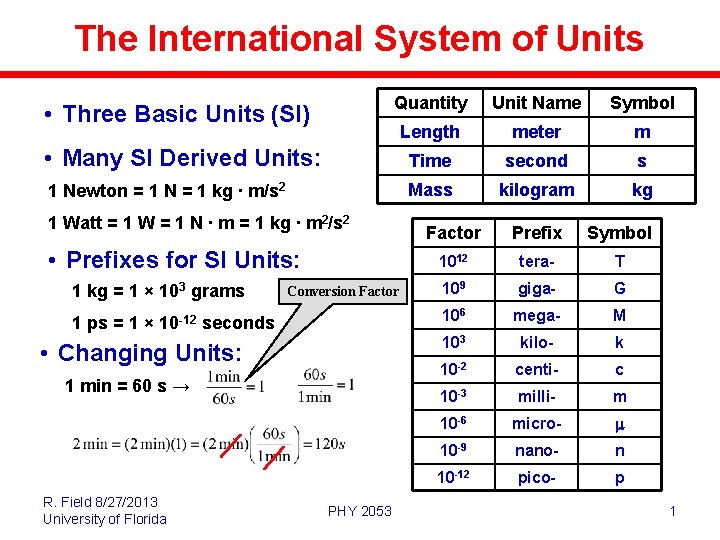
The International System of Units Quantity Unit Name Symbol Length meter m • Many SI Derived Units: Time second s 1 Newton = 1 N = 1 kg ∙ m/s 2 Mass kilogram kg • Three Basic Units (SI) 1 Watt = 1 W = 1 N ∙ m = 1 kg ∙ m 2/s 2 • Prefixes for SI Units: 1 kg = 1 × 103 grams Conversion Factor 1 ps = 1 × 10 -12 seconds • Changing Units: 1 min = 60 s → R. Field 8/27/2013 University of Florida PHY 2053 Factor Prefix Symbol 1012 tera- T 109 giga- G 106 mega- M 103 kilo- k 10 -2 centi- c 10 -3 milli- m 10 -6 micro- m 10 -9 nano- n 10 -12 pico- p 1

distance: meter 1791: one ten-millionth of a quadrant of the Earth… --1889: platinum-iridium bar --1983: The meter is the length of the path traveled by light in vacuum during a time interval of 1 / (299, 792, 458) of a second (i. e. , by definition, c = 299, 792, 458 m/s) R. Field 8/27/2013 University of Florida PHY 2053 2

time: second Since long ago (Egyptians and Greeks): 1 day = 24 hours 1 s = (1/24) x (1/60) of the full Earth turn However, the Earth rotation period varies by a few ms… 1967: The second is the duration of 9, 192, 631, 770 periods of the radiation emitted by caesium-133 atom R. Field 8/27/2013 University of Florida PHY 2053 3

mass: kilogram 1799: 10 x 10 cm 3 of water 1 u = 1. 66053886 × 10 --1899: platinum-iridium cylinder (d=h=39 mm) -27 kg atomic mass unit (u): • 12 u = mass of 12 C atom • universal, reproducible, nor requiring an artifact Density: The density of a material, r, is the mass per unit volume: r = m/V r(water) = 1. 00 g/cm 3 R. Field 8/27/2013 University of Florida PHY 2053 4

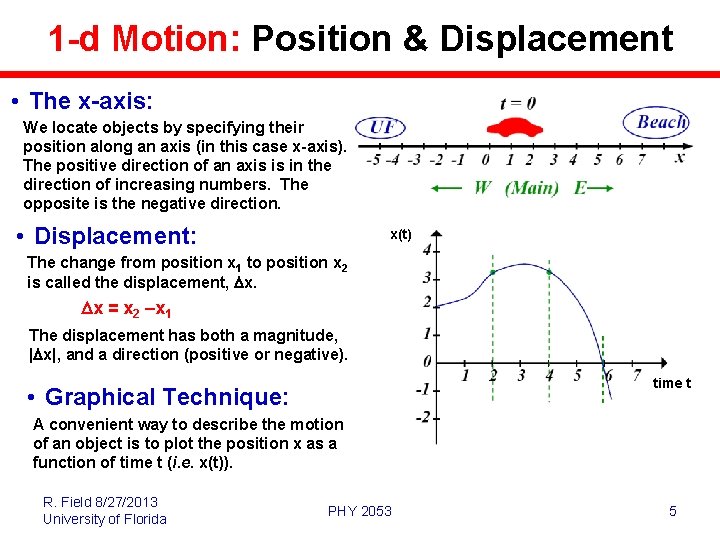
1 -d Motion: Position & Displacement • The x-axis: We locate objects by specifying their position along an axis (in this case x-axis). The positive direction of an axis is in the direction of increasing numbers. The opposite is the negative direction. • Displacement: x(t) The change from position x 1 to position x 2 is called the displacement, Dx. Dx = x 2 –x 1 The displacement has both a magnitude, |Dx|, and a direction (positive or negative). time t • Graphical Technique: A convenient way to describe the motion of an object is to plot the position x as a function of time t (i. e. x(t)). R. Field 8/27/2013 University of Florida PHY 2053 5

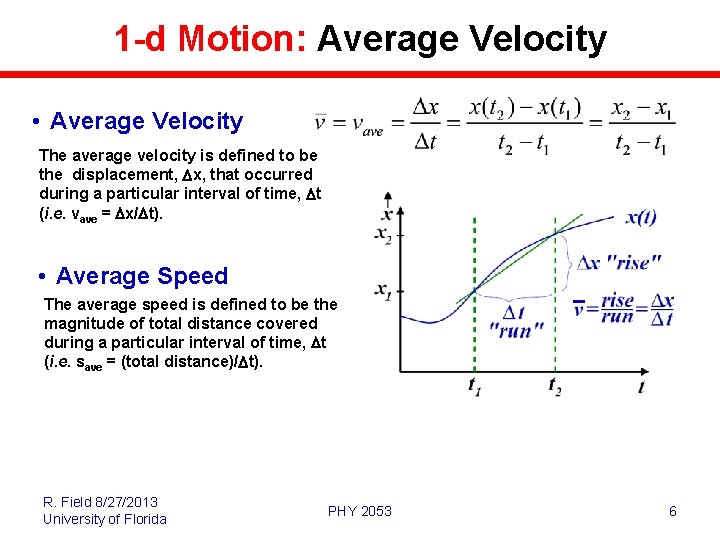
1 -d Motion: Average Velocity • Average Velocity The average velocity is defined to be the displacement, Dx, that occurred during a particular interval of time, Dt (i. e. vave = Dx/Dt). • Average Speed The average speed is defined to be the magnitude of total distance covered during a particular interval of time, Dt (i. e. save = (total distance)/Dt). R. Field 8/27/2013 University of Florida PHY 2053 6

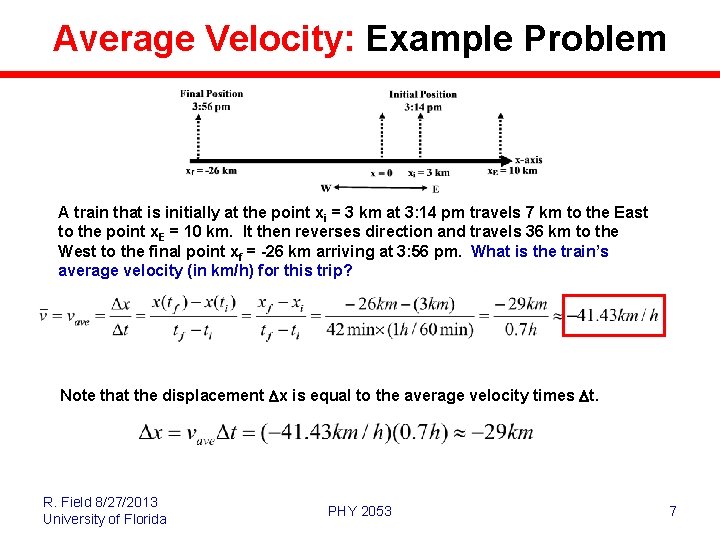
Average Velocity: Example Problem A train that is initially at the point xi = 3 km at 3: 14 pm travels 7 km to the East to the point x. E = 10 km. It then reverses direction and travels 36 km to the West to the final point xf = -26 km arriving at 3: 56 pm. What is the train’s average velocity (in km/h) for this trip? Note that the displacement Dx is equal to the average velocity times Dt. R. Field 8/27/2013 University of Florida PHY 2053 7

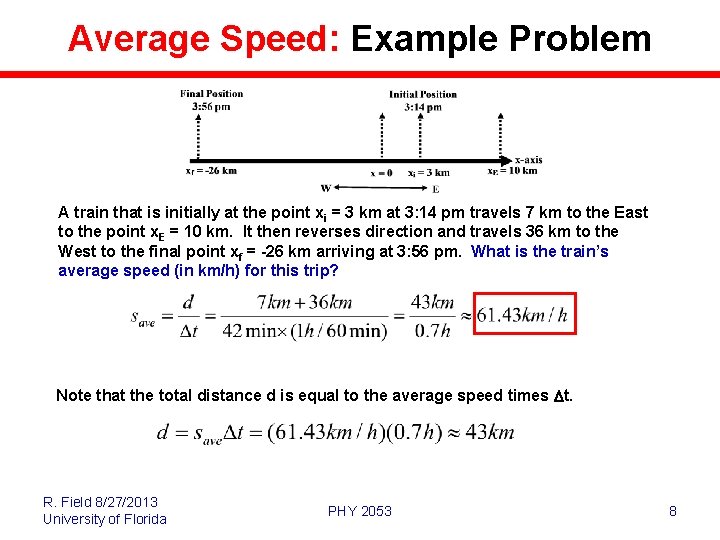
Average Speed: Example Problem A train that is initially at the point xi = 3 km at 3: 14 pm travels 7 km to the East to the point x. E = 10 km. It then reverses direction and travels 36 km to the West to the final point xf = -26 km arriving at 3: 56 pm. What is the train’s average speed (in km/h) for this trip? Note that the total distance d is equal to the average speed times Dt. R. Field 8/27/2013 University of Florida PHY 2053 8

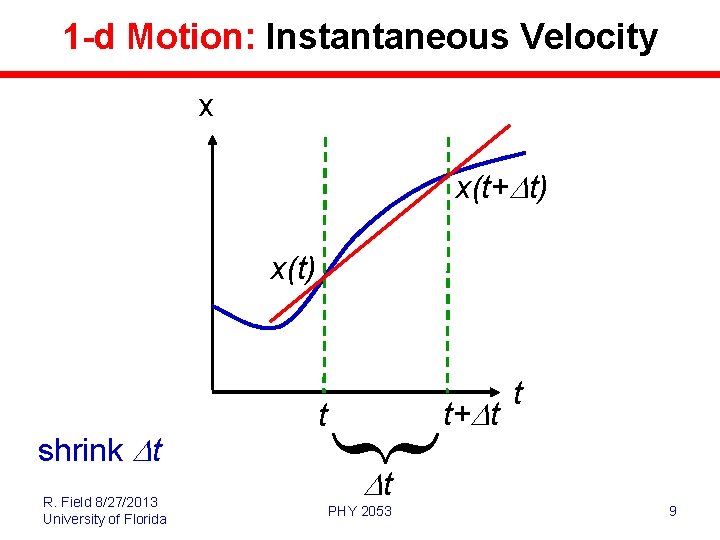
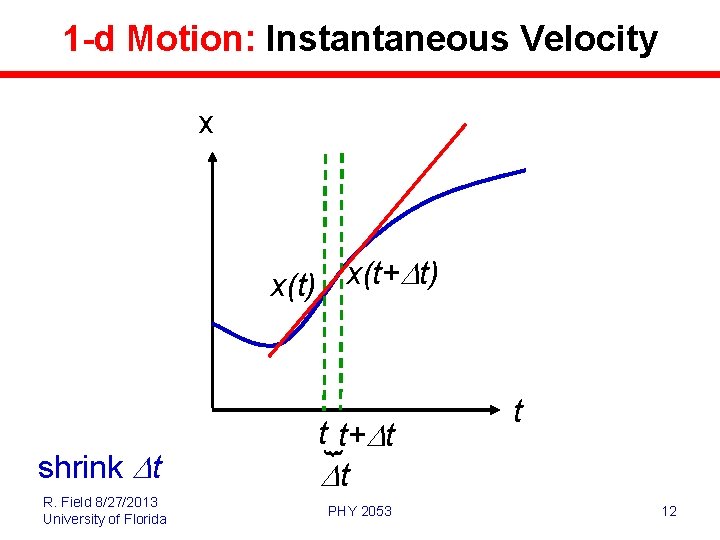
1 -d Motion: Instantaneous Velocity x x(t+Dt) x(t) R. Field 8/27/2013 University of Florida shrink Dt t t+Dt t Dt PHY 2053 9

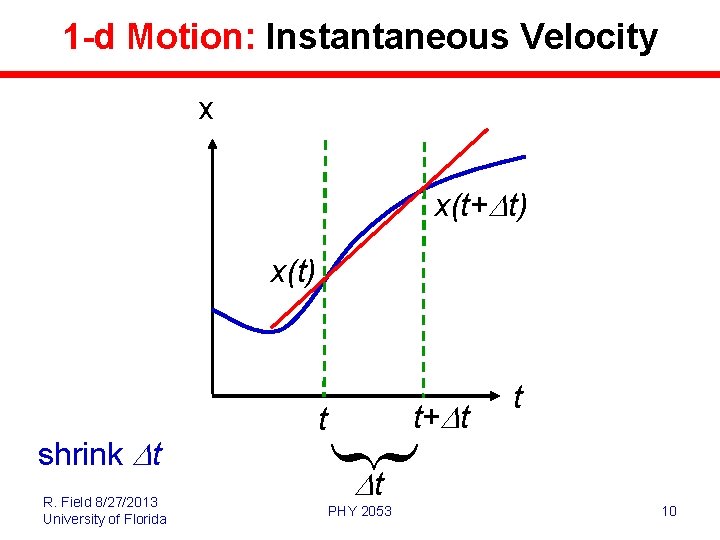
1 -d Motion: Instantaneous Velocity x x(t+Dt) x(t) R. Field 8/27/2013 University of Florida shrink Dt t+Dt t t Dt PHY 2053 10

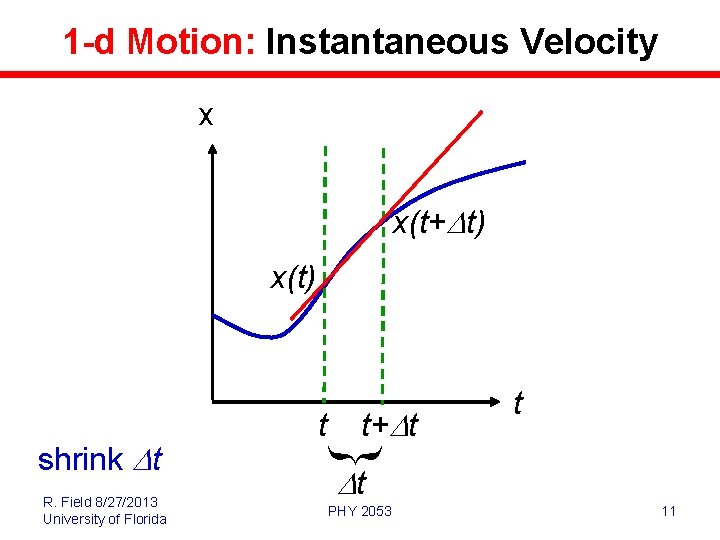
1 -d Motion: Instantaneous Velocity x x(t+Dt) x(t) R. Field 8/27/2013 University of Florida t+Dt shrink Dt t t Dt PHY 2053 11

1 -d Motion: Instantaneous Velocity x x(t+ D t) x(t) R. Field 8/27/2013 University of Florida shrink Dt t t+Dt Dt t PHY 2053 12

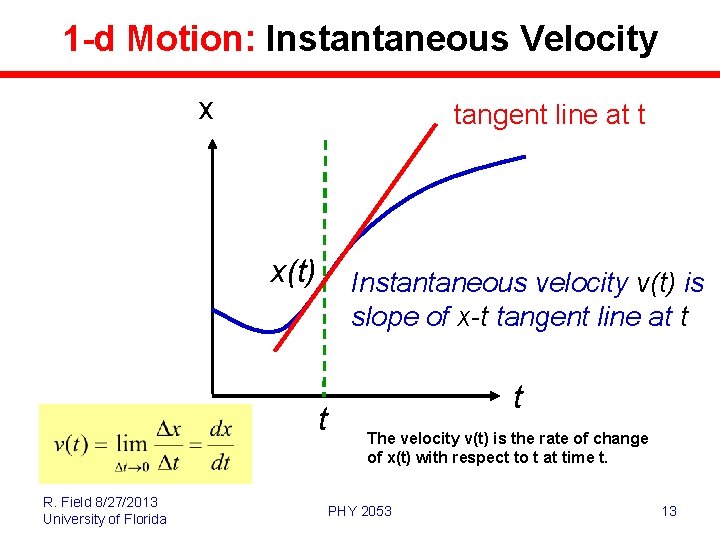
1 -d Motion: Instantaneous Velocity x tangent line at t x(t) Instantaneous velocity v(t) is slope of x-t tangent line at t t R. Field 8/27/2013 University of Florida t The velocity v(t) is the rate of change of x(t) with respect to t at time t. PHY 2053 13

1 -d Motion: Acceleration • Acceleration When a particles velocity changes, the particle is said to undergo acceleration (i. e. accelerate). v v(t) v 2 • Average Acceleration Dv “rise” v 1 The average acceleration is defined to be the change in velocity, Dv, that occurred during a particular interval of time, Dt (i. e. aave = Dv/Dt). • Instantaneous Acceleration a Dv v The acceleration a(t) is the rate of change of v(t) with respect to t at time t. v(t) R. Field 8/27/2013 University of Florida PHY 2053 Instantaneous acceleration a(t) is slope of v-t tangent line at t 14

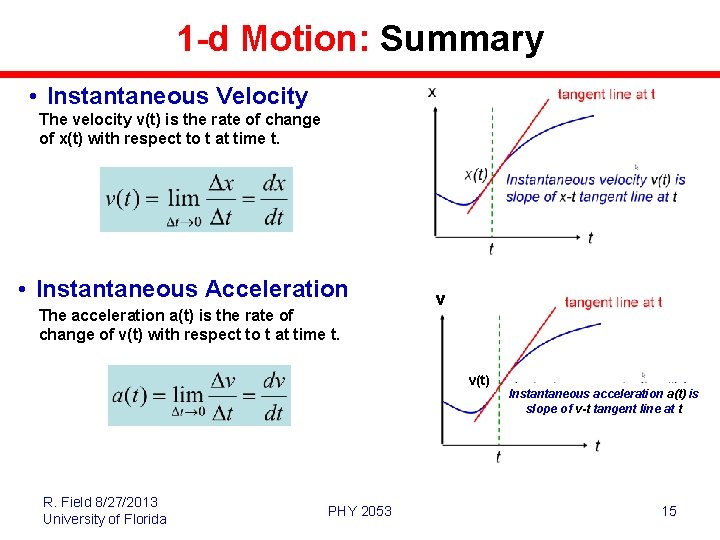
1 -d Motion: Summary • Instantaneous Velocity The velocity v(t) is the rate of change of x(t) with respect to t at time t. • Instantaneous Acceleration The acceleration a(t) is the rate of change of v(t) with respect to t at time t. v v(t) R. Field 8/27/2013 University of Florida PHY 2053 Instantaneous acceleration a(t) is slope of v-t tangent line at t 15