The Ins and Outs of Gradual Type Inference

The Ins and Outs of Gradual Type Inference Aseem Rastogi Stony Brook University Avik Chaudhuri Basil Hosmer Adobe Systems

Gradually Typed Code e. g. , a Flash application Statically Dynamically type Typed Code in Action. Script casts missing annotations = dynamic types fully annotated with static types 2

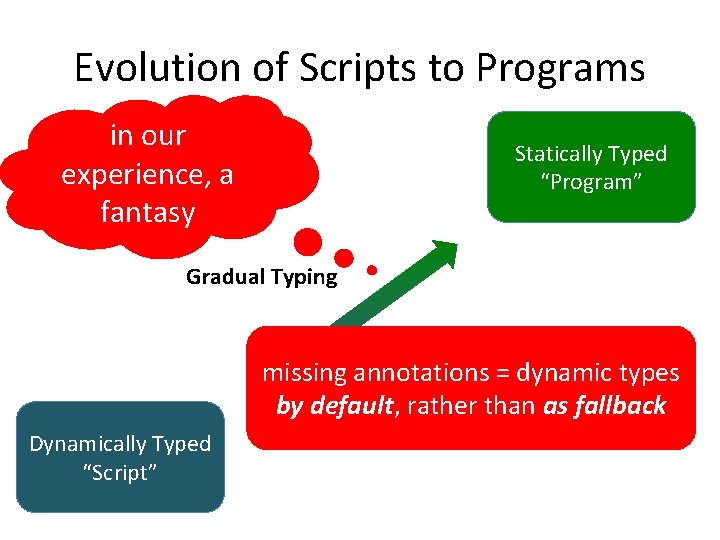
Evolution of Scripts to Programs in our experience, a fantasy Statically Typed “Program” Gradual Typing incrementally adding missingannotations = dynamic types for performance by default, rather than as fallback Dynamically Typed “Script”

Annoying Trade-Off Can this Performance Annotation trade-off be Penalty Burden eliminated? 4

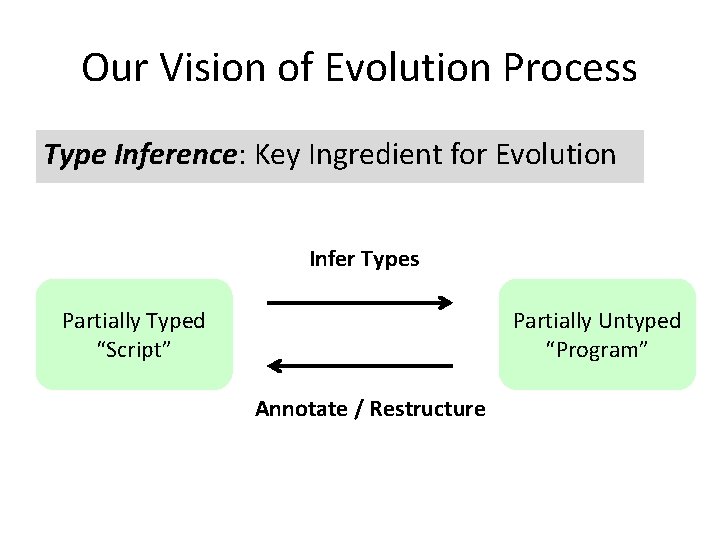
Our Vision of Evolution Process Type Inference: Key Ingredient for Evolution Infer Types Partially Typed “Script” Partially Untyped “Program” Annotate / Restructure

Our Contributions Gradual Type • Type Inference Algorithm for programs should not Gradually Typed Languages Inference Practical Motivation Goal Non Goal break, even when run in • arbitrary Improve Performance of environments Flash Applications must admit reasoning outside • Backward Compatibility … by eliminating the static typeas many type casts as system possible • Increase Safety / Eliminate Errors 6

Gradual Type Inference 7

A Gradually Typed Program function foo(n: Number) { var s = 0; var i = s; while(i < n) { s = s + i; i = i + 1; } return s; } 8

Gradual Typing: No Type Inference function foo(n: Number): * { var s: * = 0; var i: * = s; while(i < n) { s = s + i; i = i + 1; } return s; } Missing Type = Dynamic Type 9

Gradual Typing: No Type Inference function foo(n: Number): * < : (Number, Number) Boolean + : (Number, Number) Number { var s: * = �Number ▷ *� 0; var i: * = s; Type Casts while(i < n) { s = s + i; i = i + 1; } return s; Missing Type = Dynamic Type } 10

Gradual Typing: No Type Inference function foo(n: Number): * < : (Number, Number) Boolean + : (Number, Number) Number { var s: * = �Number ▷ *� 0; var i: * = s; while(�* ▷ Number�i < n) { s = s + i; i = i + 1; } return s; Missing Type = Dynamic Type } 11

Gradual Typing: No Type Inference function foo(n: Number): * < : (Number, Number) Boolean + : (Number, Number) Number { var s: * = �Number ▷ *� 0; var i: * = s; while(�* ▷ Number�i < n) { s = �Number ▷ *�(�* ▷ Number�s + �* ▷ Number�i); i = i + 1; } return s; Missing Type = Dynamic Type } 12

Gradual Typing: No Type Inference function foo(n: Number): * < : (Number, Number) Boolean + : (Number, Number) Number { var s: * = �Number ▷ *� 0; var i: * = s; while(�* ▷ Number�i < n) { s = �Number ▷ *�(�* ▷ Number�s + �* ▷ Number�i); i = �Number ▷ *�(�* ▷ Number�i + 1); } return s; Missing Type = Dynamic Type } 13

Gradual Typing: No Type Inference function foo(n: Number): * Performance { Penalty var s: * = �Number ▷ *� 0; var i: * = s; while(�* ▷ Number�i < n) { s = �Number ▷ *�(�* ▷ Number�s + �* ▷ Number�i); i = �Number ▷ *�(�* ▷ Number�i + 1); } return s; Missing Type = Dynamic Type } 14

Gradual Typing: Type Inference function foo(n: Number): Foo! { Unknown types represented as var s: S = 0; type variables, var i: I = s; solved to static types where possible, while(i < n) { dynamic type as fallback s = s + i; i = i + 1; } Missing Type = Unknown Type return s; Missing Type = Dynamic Type } 15

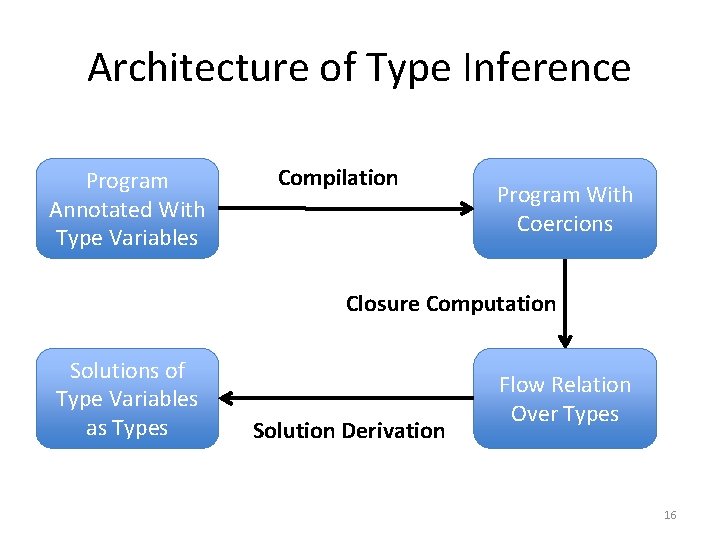
Architecture of Type Inference Program Annotated With Type Variables Compilation Program With Coercions Closure Computation Solutions of Type Variables as Types Solution Derivation Flow Relation Over Types 16

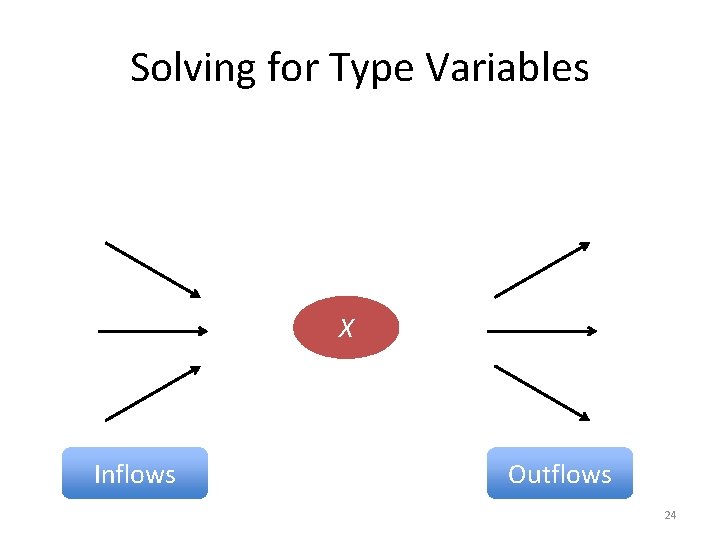
Coercions … are of the form T 1 ▷ T 2 “term of type T 1 flows into context of type T 2” T ▷ X is an inflow for type variable X X ▷ T is an outflow for type variable X 17

Generating Coercions function foo(n: Number): Foo! { var s: S = �Number ▷ S� 0; var i: I = s; while(i < n) { s = s + i; i = i + 1; } return s; } Number ▷ S 18

Generating Coercions function foo(n: Number): Foo! { var s: S = �Number ▷ S� 0; var i: I = �S ▷ I�s; while(i < n) { s = s + i; i = i + 1; } return s; } Number ▷ S S▷I 19

Generating Coercions function foo(n: Number): Foo! { var s: S = �Number ▷ S� 0; var i: I = �S ▷ I�s; while(�I ▷ Number�i < n) { s = s + i; i = i + 1; } return s; } Number ▷ S S▷I I ▷ Number 20

Generating Coercions Number ▷ S function foo(n: Number): Foo! { S▷I var s: S = �Number ▷ S� 0; I ▷ Number var i: I = �S ▷ I�s; S ▷ Number while(�I ▷ Number�i < n) { s = �Number ▷ S> (�S ▷ Number�s + �I ▷ Number�i); i = i + 1; } return s; } 21

Generating Coercions Number ▷ S function foo(n: Number): Foo! { S▷I var s: S = �Number ▷ S� 0; I ▷ Number var i: I = �S ▷ I�s; S ▷ Number while(�I ▷ Number�i < n) { s = �Number ▷ S�(�S ▷ Number�s + �I ▷ Number�i); i = �Number ▷ I�(�I ▷ Number�i + 1); Number ▷ I } return s; } 22

Generating Coercions Number ▷ S function foo(n: Number): Foo! { S▷I var s: S = �Number ▷ S� 0; I ▷ Number var i: I = �S ▷ I�s; S ▷ Number while(�I ▷ Number�i < n) { s = �Number ▷ S�(�S ▷ Number�s + �I ▷ Number�i); i = �Number ▷ I�(�I ▷ Number�i + 1); Number ▷ I } return �S ▷ Foo!�s; S ▷ Foo! } 23

Solving for Type Variables X Inflows Outflows 24

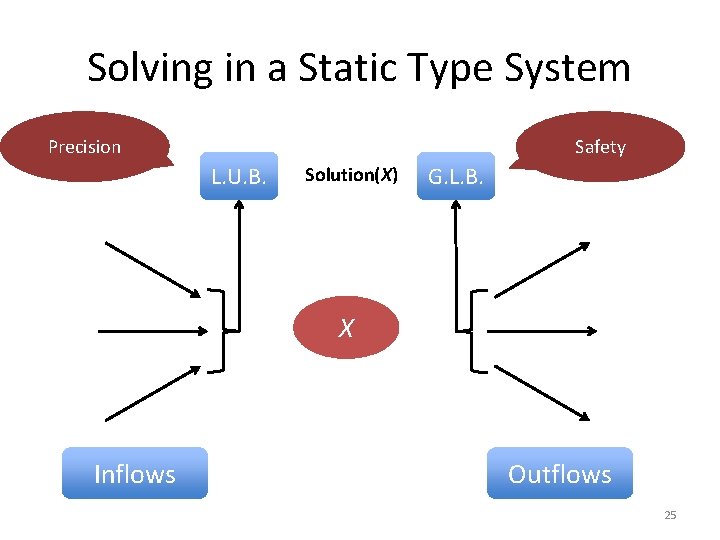
Solving in a Static Type System Precision Safety L. U. B. Solution(X) G. L. B. X Inflows Outflows 25

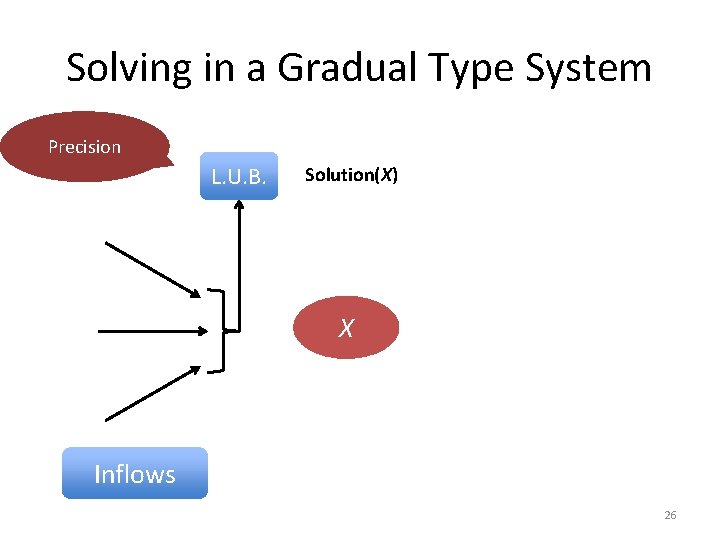
Solving in a Gradual Type System Precision L. U. B. Solution(X) X Inflows 26

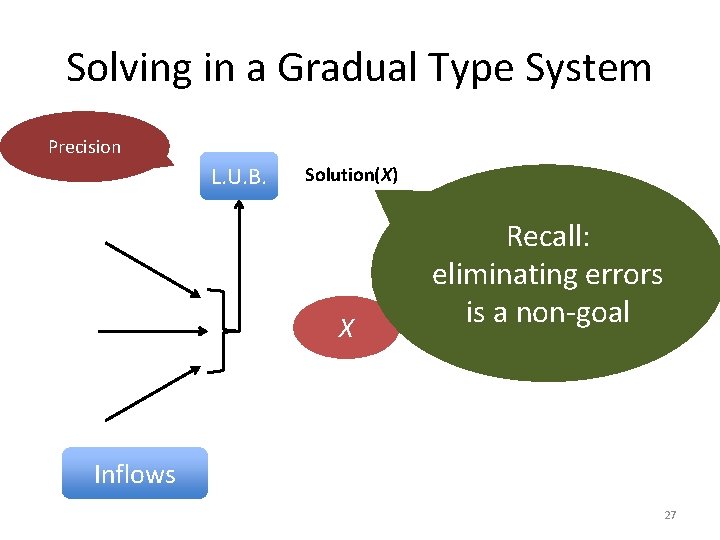
Solving in a Gradual Type System Precision L. U. B. Solution(X) X Recall: eliminating errors is a non-goal Inflows 27

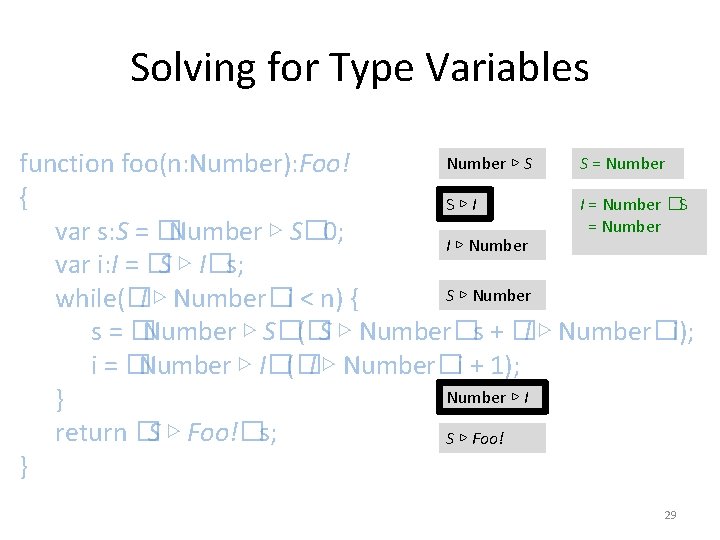
Solving for Type Variables Number ▷ S S = Number function foo(n: Number): Foo! { S▷I var s: S = �Number ▷ S� 0; I ▷ Number var i: I = �S ▷ I�s; S ▷ Number while(�I ▷ Number�i < n) { s = �Number ▷ S�(�S ▷ Number�s + �I ▷ Number�i); i = �Number ▷ I�(�I ▷ Number�i + 1); Number ▷ I } return �S ▷ Foo!�s; S ▷ Foo! } 28

Solving for Type Variables Number ▷ S S = Number function foo(n: Number): Foo! { S▷I I = Number �S = Number var s: S = �Number ▷ S� 0; I ▷ Number var i: I = �S ▷ I�s; S ▷ Number while(�I ▷ Number�i < n) { s = �Number ▷ S�(�S ▷ Number�s + �I ▷ Number�i); i = �Number ▷ I�(�I ▷ Number�i + 1); Number ▷ I } return �S ▷ Foo!�s; S ▷ Foo! } 29

Solving for Type Variables Number ▷ S S = Number function foo(n: Number): Foo! { S▷I I = Number �S = Number var s: S = �Number ▷ S� 0; I ▷ Number var i: I = �S ▷ I�s; S ▷ Number while(�I ▷ Number�i < n) { s = �Number ▷ S�(�S ▷ Number�s + �I ▷ Number�i); i = �Number ▷ I�(�I ▷ Number�i + 1); Number ▷ I } return �S ▷ Foo!�s; S ▷ Foo! = S = Number } 30

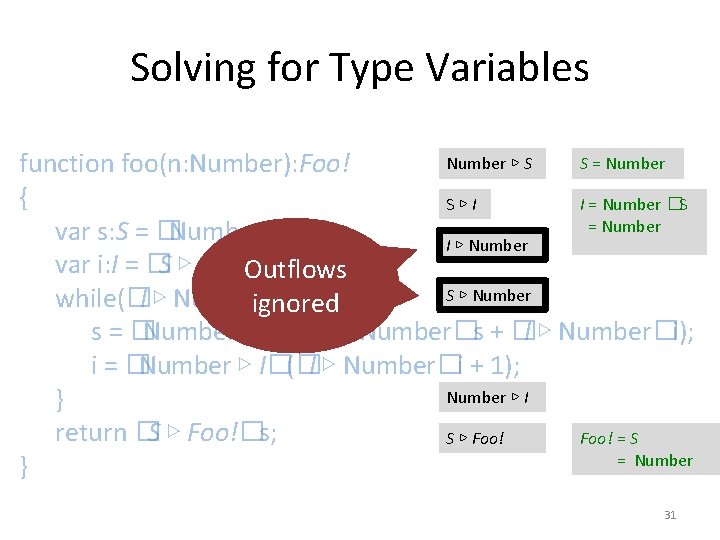
Solving for Type Variables Number ▷ S S = Number function foo(n: Number): Foo! { S▷I I = Number �S = Number var s: S = �Number ▷ S� 0; I ▷ Number var i: I = �S ▷ I�s; Outflows S ▷ Number while(�I ▷ Number� i < n) { ignored s = �Number ▷ S�(�S ▷ Number�s + �I ▷ Number�i); i = �Number ▷ I�(�I ▷ Number�i + 1); Number ▷ I } return �S ▷ Foo!�s; S ▷ Foo! = S = Number } 31

Annotated Program function foo(n: Number): Number { var s: Number = �Number ▷ Number� 0; var i: Number = �Number ▷ Number�s; while(�Number ▷ Number�i < n) { s = �Number ▷ Number�(�Number ▷ Number�s + �Number ▷ Number�i); i = �Number ▷ Number�(�Number ▷ Number�i + 1); } return �Number ▷ Number�s; } 32

Annotated Program: No Casts function foo(n: Number): Number { var s: Number = 0; var i: Number = s; while(i < n) { s = s + i; i = i + 1; } return s; } 33

Summarizing… Key Idea (1) Consider Only Inflows to Solve Type Variables 34

Type Inference for Higher Order Types var x: X = function(y: Number): Number { … }; If(b) { x = function(y: Boolean): Number { … }; x(true); } 35

Type Inference for Higher Order Types var x: X = function(y: Number): Number { … }; If(b) { Number x = function(y: Boolean): Number { … }; x(true); Boolean } Number ▷ X 36

Type Inference for Higher Order Types var x: X = function(y: Number): Number { … }; If(b) { Number x = function(y: Boolean): Number { … }; x(true); Boolean } X=⊥ Number ▷ X Number 37

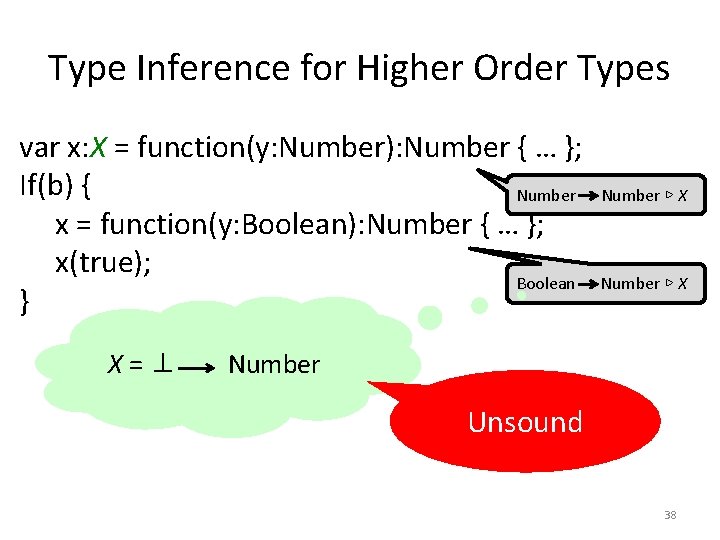
Type Inference for Higher Order Types var x: X = function(y: Number): Number { … }; If(b) { Number x = function(y: Boolean): Number { … }; x(true); Boolean } X=⊥ Number ▷ X Number Unsound 38

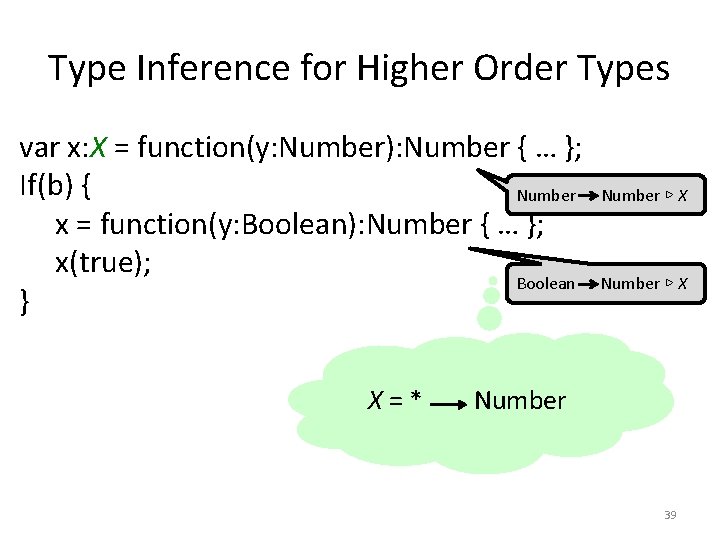
Type Inference for Higher Order Types var x: X = function(y: Number): Number { … }; If(b) { Number x = function(y: Boolean): Number { … }; x(true); Boolean } X=* Number ▷ X Number 39

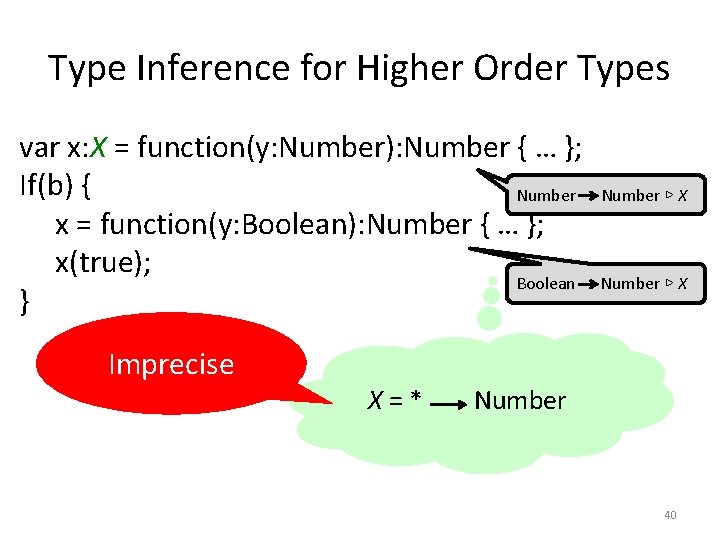
Type Inference for Higher Order Types var x: X = function(y: Number): Number { … }; If(b) { Number x = function(y: Boolean): Number { … }; x(true); Boolean } Number ▷ X Imprecise X=* Number 40

Type Inference for Higher Order Types var x: X = function(y: Number): Number { … }; If(b) { Number x = function(y: Boolean): Number { … }; x(true); Boolean } X = Boolean Number ▷ X Number 41

Higher Order Types: Kinds 42

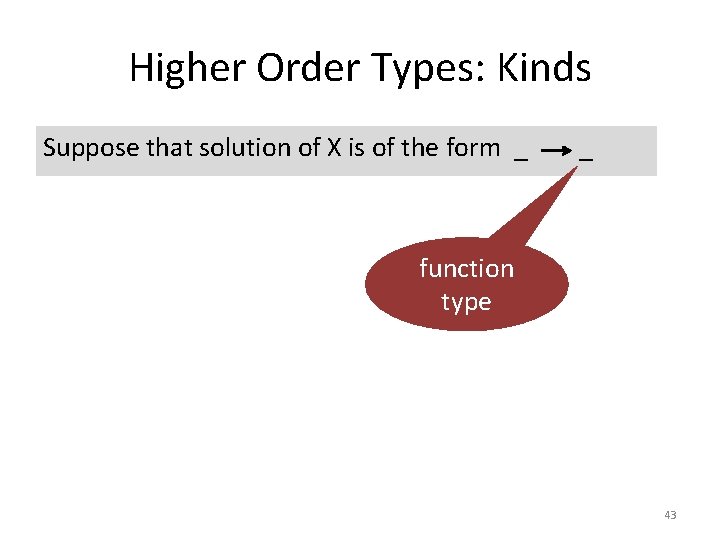
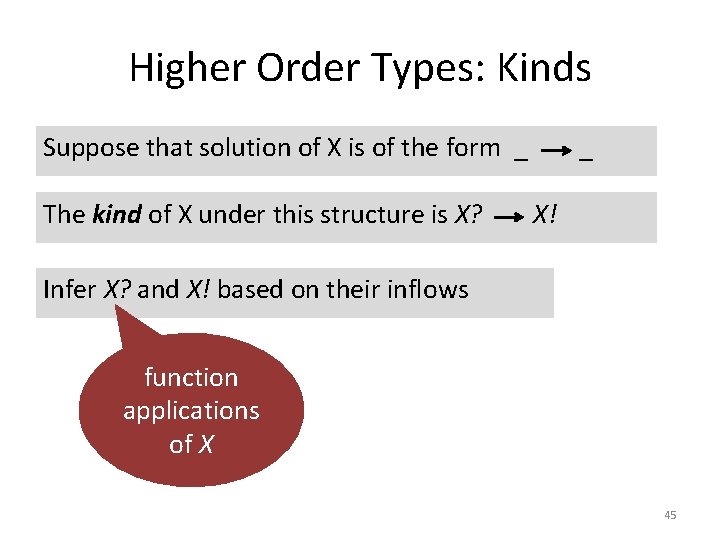
Higher Order Types: Kinds Suppose that solution of X is of the form _ _ function type 43

Higher Order Types: Kinds Suppose that solution of X is of the form _ The kind of X under this structure is X? _ X! 44

Higher Order Types: Kinds Suppose that solution of X is of the form _ The kind of X under this structure is X? _ X! Infer X? and X! based on their inflows function applications of X 45

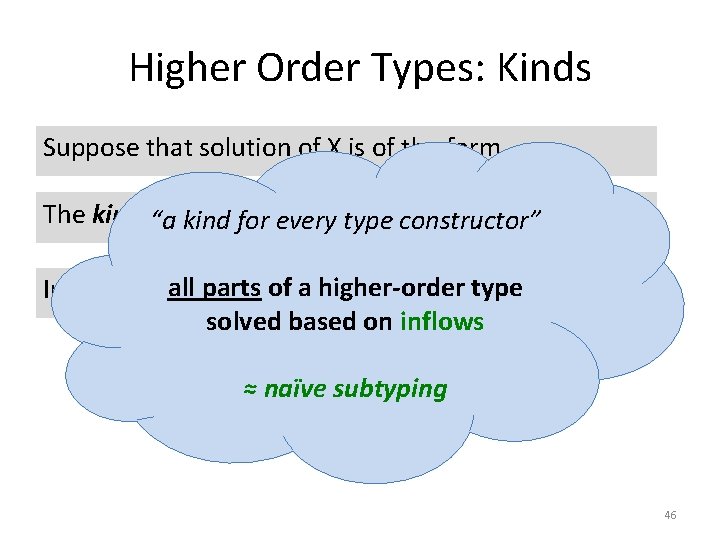
Higher Order Types: Kinds Suppose that solution of X is of the form _ _ The kind of under structure is X? X! “a Xkind for this every type constructor” ofon a higher-order Infer X? andall. X!parts based their Inflows type solved based on inflows ≈ naïve subtyping 46

Type Inference for Higher Order Types var x: X = function(y: Number): Number { … }; Number ▷ X if(b) { Boolean x = function(y: Boolean): Number { … }; Number ▷ X? X! x(true); X? X! ▷ X } Boolean Number ▷ X 47

Type Inference for Higher Order Types var x: X = function(y: Number): Number { … }; Number ▷ X if(b) { x = function(y: Boolean): Number. Boolean { … }; Number ▷ X? X! x(true); X? X! ▷ X } Boolean Number ▷ X Boolean ▷ X? 48

Type Inference for Higher Order Types var x: X = function(y: Number): Number { … }; Number ▷ X if(b) { x = function(y: Boolean): Number. Boolean { … }; Number ▷ X? X! x(true); X? X! ▷ X } Boolean Number ▷ X Boolean ▷ X? X? ▷ Boolean Number ▷ X! 49

Type Inference for Higher Order Types var x: X = function(y: Number): Number { … }; Number ▷ X if(b) { x = function(y: Boolean): Number. Boolean { … }; Number ▷ X? X! x(true); X? X! ▷ X } Boolean Number ▷ X Boolean ▷ X? X? ▷ Boolean Number ▷ X! X? ▷ Number 50

Type Inference for Higher Order Types var x: X = function(y: Number): Number { … }; Number ▷ X if(b) { x = function(y: Boolean): Number. Boolean { … }; Number ▷ X? X! x(true); X? X! ▷ X } Boolean X? = Boolean Number ▷ X Boolean ▷ X? X? ▷ Boolean Number ▷ X! X? ▷ Number 51

Type Inference for Higher Order Types var x: X = function(y: Number): Number { … }; Number ▷ X if(b) { x = function(y: Boolean): Number. Boolean { … }; Number ▷ X? X! x(true); X? X! ▷ X } Boolean X? = Boolean Number ▷ X Boolean ▷ X? X? ▷ Boolean X! = Number ▷ X! X? ▷ Number 52

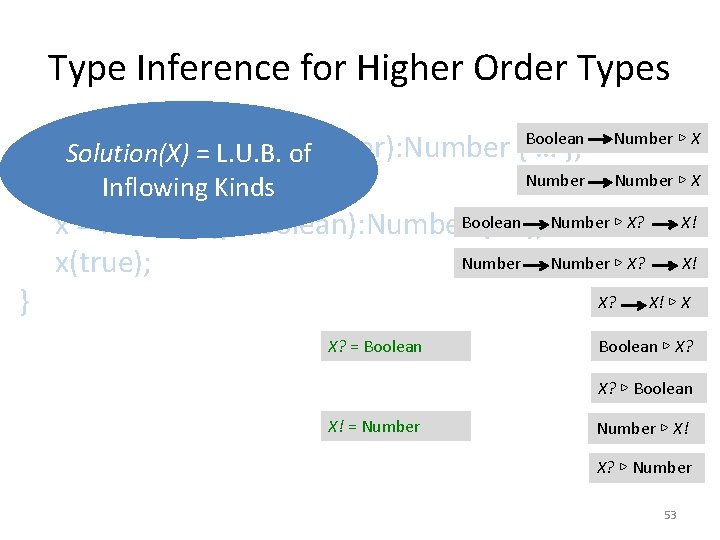
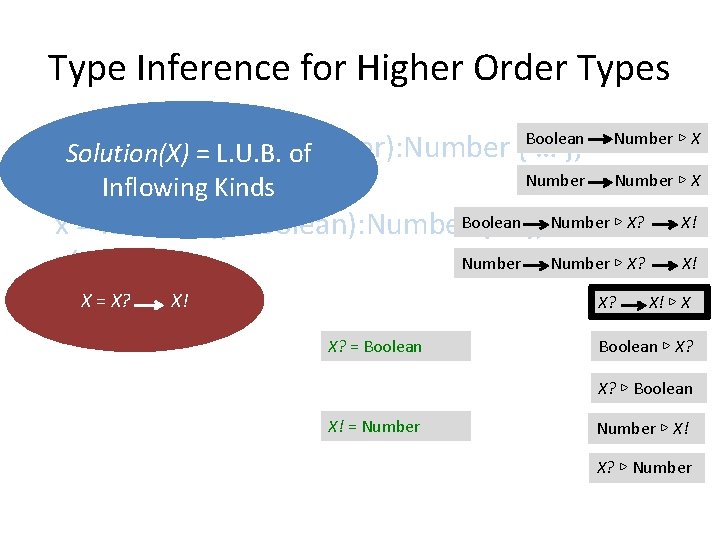
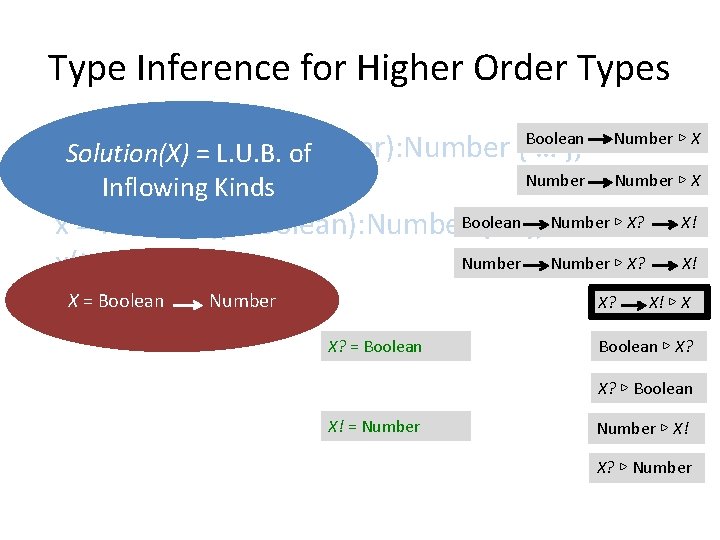
Type Inference for Higher Order Types var Solution(X) x: X = function(y: Number): Number { … }; = L. U. B. of Number ▷ X if(b) { Inflowing Kinds x = function(y: Boolean): Number. Boolean { … }; Number ▷ X? X! x(true); X? X! ▷ X } Boolean X? = Boolean Number ▷ X Boolean ▷ X? X? ▷ Boolean X! = Number ▷ X! X? ▷ Number 53

Type Inference for Higher Order Types var Solution(X) x: X = function(y: Number): Number { … }; = L. U. B. of Number ▷ X if(b) { Inflowing Kinds x = function(y: Boolean): Number. Boolean { … }; Number ▷ X? X! x(true); X = X? X! ▷ X } Boolean X? = Boolean Number ▷ X Boolean ▷ X? X? ▷ Boolean X! = Number ▷ X! X? ▷ Number

Type Inference for Higher Order Types var Solution(X) x: X = function(y: Number): Number { … }; = L. U. B. of Number ▷ X if(b) { Inflowing Kinds x = function(y: Boolean): Number. Boolean { … }; Number ▷ X? X! x(true); X? X! ▷ X } X = Boolean Number Boolean X? = Boolean Number ▷ X Boolean ▷ X? X? ▷ Boolean X! = Number ▷ X! X? ▷ Number

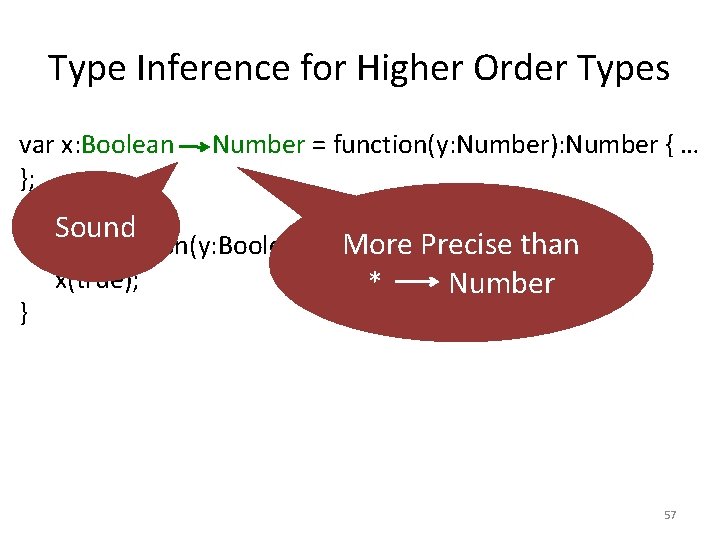
Type Inference for Higher Order Types var x: Boolean Number = function(y: Number): Number { … }; if(b) { x = function(y: Boolean): Number { … }; x(true); } 56

Type Inference for Higher Order Types var x: Boolean Number = function(y: Number): Number { … }; if(b) { Sound x = function(y: Boolean): Number { … }; than More Precise x(true); * Number } 57

Summarizing… Key Idea (2) Use Kinds to Infer Higher Order Types 58

Public Functions function foo(x: Foo? ): Foo! { if(b) { return x + 1; } else { return 0; } } foo(1); 59

Public Functions function foo(x: Foo? ): Foo! { Foo? ▷ Number if(b) { return x + 1; Number ▷ Foo! } else { return 0; Number ▷ Foo! } } foo(1); Number ▷ Foo? Foo! = Number Foo? = Number 60

Public Functions function foo(x: *): * { if(b) { return x + 1; } else { return 0; } } function foo(x: Number): Number { if(b) { return x + 1; } else { return 0; } } foo(1); 61

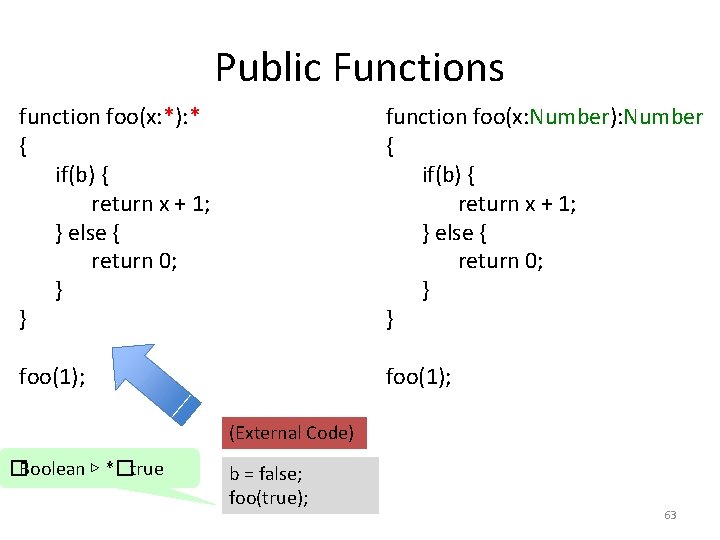
Public Functions function foo(x: *): * { if(b) { return x + 1; } else { return 0; } } function foo(x: Number): Number { if(b) { return x + 1; } else { return 0; } } foo(1); (External Code) b = false; foo(true); 62

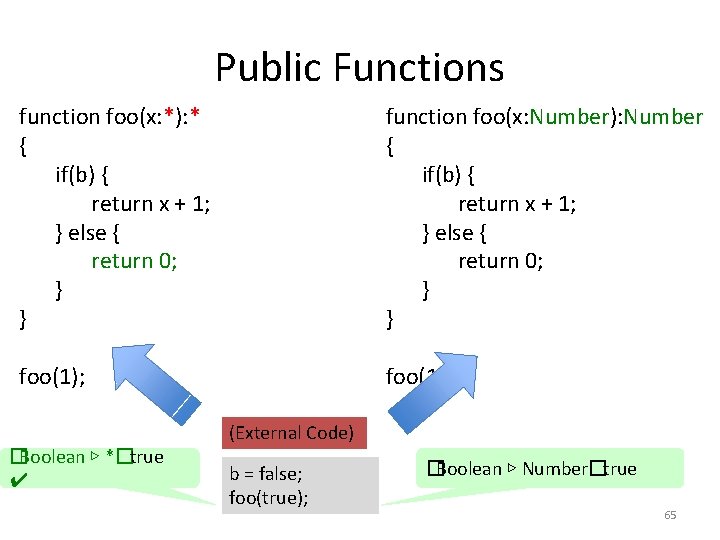
Public Functions function foo(x: *): * { if(b) { return x + 1; } else { return 0; } } function foo(x: Number): Number { if(b) { return x + 1; } else { return 0; } } foo(1); (External Code) �Boolean ▷ *�true b = false; foo(true); 63

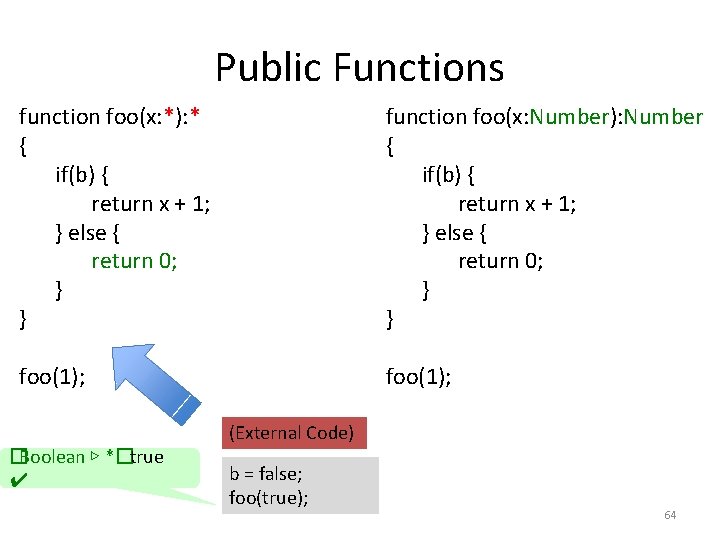
Public Functions function foo(x: *): * { if(b) { return x + 1; } else { return 0; } } function foo(x: Number): Number { if(b) { return x + 1; } else { return 0; } } foo(1); �Boolean ▷ *�true ✔ (External Code) b = false; foo(true); 64

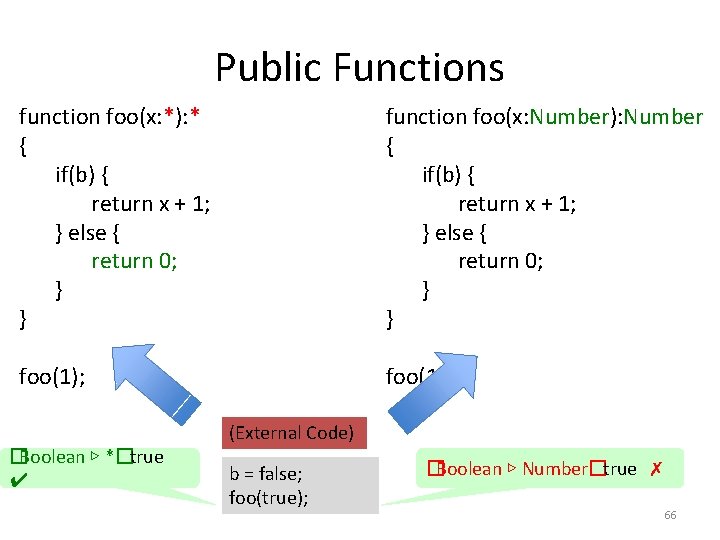
Public Functions function foo(x: *): * { if(b) { return x + 1; } else { return 0; } } function foo(x: Number): Number { if(b) { return x + 1; } else { return 0; } } foo(1); �Boolean ▷ *�true ✔ (External Code) b = false; foo(true); �Boolean ▷ Number�true 65

Public Functions function foo(x: *): * { if(b) { return x + 1; } else { return 0; } } function foo(x: Number): Number { if(b) { return x + 1; } else { return 0; } } foo(1); �Boolean ▷ *�true ✔ (External Code) b = false; foo(true); �Boolean ▷ Number�true ✗ 66

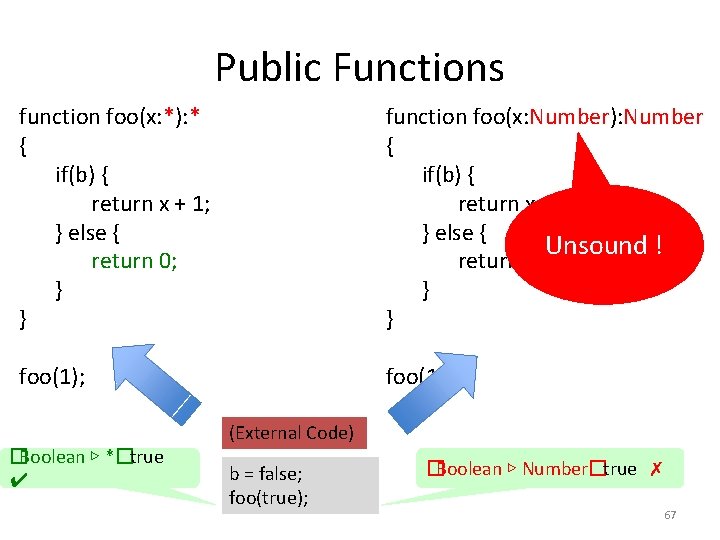
Public Functions function foo(x: *): * { if(b) { return x + 1; } else { return 0; } } function foo(x: Number): Number { if(b) { return x + 1; } else { Unsound ! return 0; } } foo(1); �Boolean ▷ *�true ✔ (External Code) b = false; foo(true); �Boolean ▷ Number�true ✗ 67

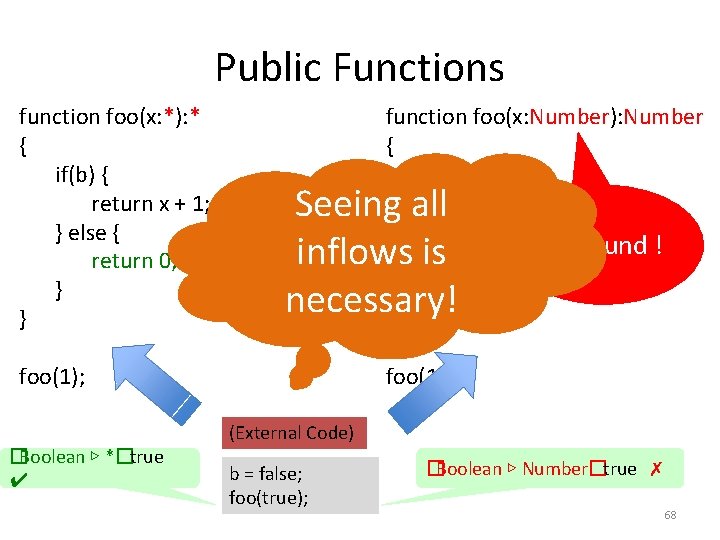
Public Functions function foo(x: *): * { if(b) { return x + 1; } else { return 0; } } function foo(x: Number): Number { if(b) { return x + 1; } else { Unsound ! return 0; } } Seeing all inflows is necessary! foo(1); �Boolean ▷ *�true ✔ foo(1); (External Code) b = false; foo(true); �Boolean ▷ Number�true ✗ 68

Where do we not see all inflows? Type variables in negative positions in the type of the program Unsafe to infer explicit annotation OR infer * 69

Summarizing… Key Idea (3) Seeing All Inflows is Necessary 70

Local Functions function bar(y: Number): Bar! { function foo(x: Foo? ): Foo! { if(b) { return x + 1; } else { return 0; } } return foo(y); } 71

Local Functions function bar(y: Number): Bar! { function foo(x: Number): Number { if(b) { return x + 1; } else { return 0; } } return foo(y); } 72

Local Functions function bar(y: Number): Bar! { function foo(x: Number): Number { if(b) { Sound ! return x + 1; } else { return 0; foo can’t be called from } External Code } return foo(y); } 73

Local Functions that Escape function bar(y: Number): Bar! { function foo(x: Foo? ): Foo! { if(b) { return x + 1; } else { return 0; } } foo(y); return foo; } 74

Local Functions that Escape function bar(y: Number): Bar! { function foo(x: Number): Number { if(b) { return x + 1; } else { return 0; } } foo(y); return foo; } 75

Local Functions that Escape function bar(y: Number): Bar! { function foo(x: Number): Number { if(b) { return x + 1; } else { Unsound ! return 0; } } foo(y); return foo; } (External Code) b = false; f = bar(1); f(true); 76

Local Functions that Escape function bar(y: Number): Bar! { function foo(x: Number): Number { if(b) { return x + 1; } else { Unsound ! return 0; Need escape } analysis? } foo(y); return foo; } (External Code) b = false; f = bar(1); f(true); 77

Local Functions that Escape function bar(y: Number): Bar! { function foo(x: Foo? ): Foo! { if(b) { return x + 1; } else { return 0; } } foo(y); return foo; } 78

Local Functions that Escape function bar(y: Number): Bar! { function foo(x: Foo? ): Foo! { if(b) { return x + 1; } else { return 0; } } Foo? Foo! ▷ Bar! foo(y); return foo; } 79

Local Functions that Escape function bar(y: Number): Bar! { function foo(x: Foo? ): Foo! { if(b) { return x + 1; } else { return 0; } } foo(y); return foo; } Foo? Foo! ▷ Bar!? Bar!! ▷ Bar! 80

Local Functions that Escape function bar(y: Number): Bar! { function foo(x: Foo? ): Foo! { if(b) { return x + 1; } else { return 0; } } foo(y); return foo; } Foo? Foo! ▷ Bar!? Bar!! ▷ Bar!? ▷ Foo? Foo! ▷ Bar!! 81

Local Functions that Escape function bar(y: Number): Bar! { function foo(x: Foo? ): Foo! { if(b) { return x + 1; } else { return 0; } } foo(y); return foo; } Foo? Foo! ▷ Bar!? Bar!! ▷ Bar!? ▷ Foo? Foo! ▷ Bar!! Bar!? is in a negative position in type of program 82

Local Functions that Escape function bar(y: Number): Bar! { function foo(x: Foo? ): Foo! { if(b) { return x + 1; } else { return 0; } } foo(y); return foo; } Foo? Foo! ▷ Bar!? Bar!! ▷ Bar!? ▷ Foo? Foo! ▷ Bar!! Bar!? is in a negative position in type of program Bar!? = * 83

Local Functions that Escape function bar(y: Number): Bar! { function foo(x: Foo? ): Foo! { if(b) { return x + 1; } else { return Foo? 0; = Bar!? = * ✔ } } foo(y); return foo; } Foo? Foo! ▷ Bar!? Bar!! ▷ Bar!? ▷ Foo? Foo! ▷ Bar!! Bar!? is in a negative position in type of program Bar!? = * 84

Local Functions that Escape Foo? Foo! ▷ Bar! function bar(y: Number): Bar! { Foo? Foo! ▷ Bar!? Bar!! function foo(x: Foo? ): Foo! { Bar!? Bar!! ▷ Bar! Foo? = * if(b) { Bar!? ▷ Foo? return x + 1; Foo! ▷ Bar!! } else { return Foo? 0; = Bar!? = * ✔ Bar!? is in a negative position } in type of program } Bar!? = * foo(y); return foo; 85 }

No Escape Analysis Necessary Polarity-based restriction on type of program + Closure compuation are already sufficient 86

Summarizing… Key Idea (4) Flows Encode Escape Analysis 87

Properties of Inference Algorithm Time Complexity: O(N 2) (“usually” O(N 3) for Languages with Subtyping) Preservation of Runtime Semantics: Programs do not break Proofs for a They can be composed with External Calculus Code of Functions and Objects 88

Implementation and Evaluation Implemented the Algorithm for Action. Script Source Language of Flash Applications 89

Implementation and Evaluation Implemented the Algorithm for Action. Script Evaluated on V 8 and Sun. Spider Benchmarks 90

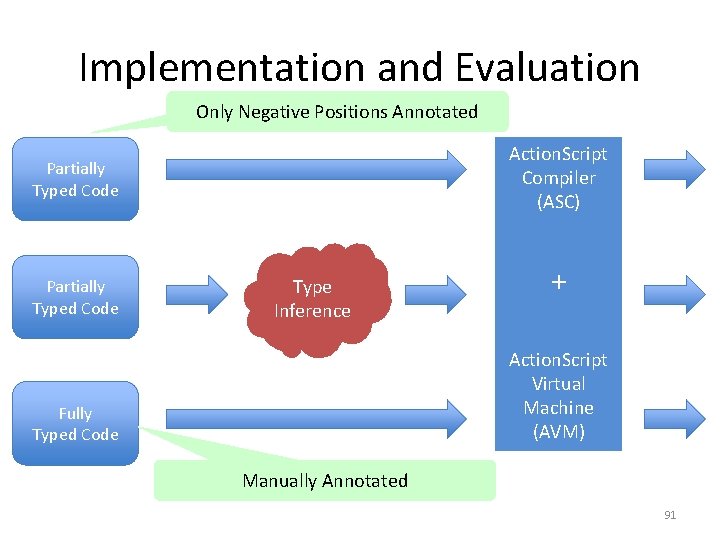
Implementation and Evaluation Only Negative Positions Annotated Action. Script Compiler (ASC) Partially Typed Code Type Inference + Action. Script Virtual Machine (AVM) Fully Typed Code Manually Annotated 91

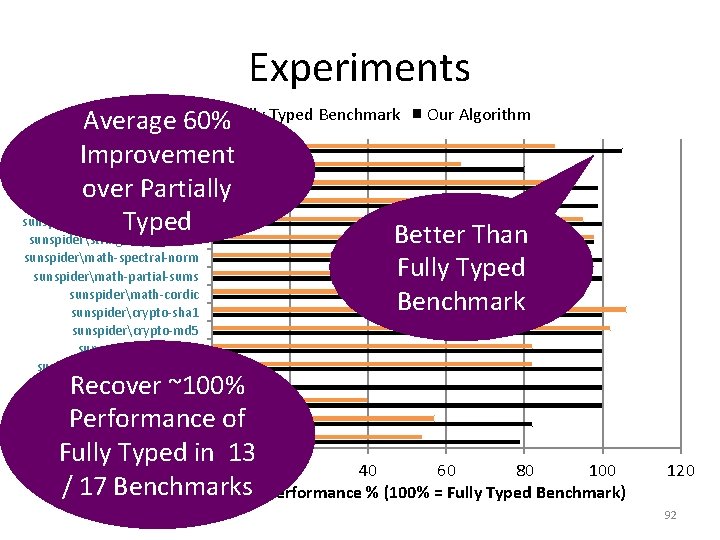
Experiments Partially Typed Benchmark Our Algorithm Average 60% v 8richards Improvement v 8raytrace v 8deltablue over Partially sunspiders 3 d-morph sunspiderstring-validate-input Typed Better Than sunspiderstring-unpack-code sunspidermath-spectral-norm sunspidermath-partial-sums sunspidermath-cordic sunspidercrypto-sha 1 sunspidercrypto-md 5 sunspidercrypto-aes sunspiderbitops-nsieve-bits sunspiderbitops-bitwise-and sunspiderbitops-bits-in-byte sunspideraccess-nsieve sunspideraccess-fankkuch Recover ~100% Performance of Fully Typed in 13 0 / 17 Benchmarks Fully Typed Benchmark 20 40 60 80 100 Performance % (100% = Fully Typed Benchmark) 120 92

Experiments Partially Typed Benchmark v 8richards v 8raytrace v 8deltablue sunspiders 3 d-morph sunspiderstring-validate-input sunspiderstring-unpack-code sunspidermath-spectral-norm sunspidermath-partial-sums sunspidermath-cordic sunspidercrypto-sha 1 sunspidercrypto-md 5 sunspidercrypto-aes sunspiderbitops-nsieve-bits sunspiderbitops-bitwise-and sunspiderbitops-bits-in-byte sunspideraccess-nsieve sunspideraccess-fankkuch Array Reads Number vs int 0 Our Algorithm Object Property Reads Range Analysis Improves Performance 20 40 60 80 100 Performance % (100% = Fully Typed Benchmark) 120 93

Things We Did Not Talk About • • How Do We Tighten Closure Computation? Do We Provide Blame Guarantees? Can Precise Types Decrease Performance? Are the Types We Infer Optimal? See Our Paper ! 94

Conclusion • Type Inference for Gradually Typed Languages • Improve performance of Flash Applications – Infer Precise Static Types for Missing Types – Consider Only Inflows for Solutions – Kinds as Solutions of Higher-Order Types • Goal: Backward Compatibility – Polarity-based Restriction on Type of Program – Escape Analysis via Closure Computation 95