The Independent Particle Approximation We approximate the strong

The Independent Particle Approximation • We approximate the strong electrostatic forces between e-s by treating the force on each electron independently, which includes force from nucleus and other electrons • Inner electrons can shield the nuclear charge, leading to “screening” Screening electron cloud The effective potential energy felt by an electron +Ze r electron Zeff is the effective charge that the electron feels and depends on r. Note that when r is inside all other electrons when r is outside all other electrons Unlike in hydrogen, in multielectron atoms the dependence of the potential energy on r due to screening lifts the degeneracy between the n states

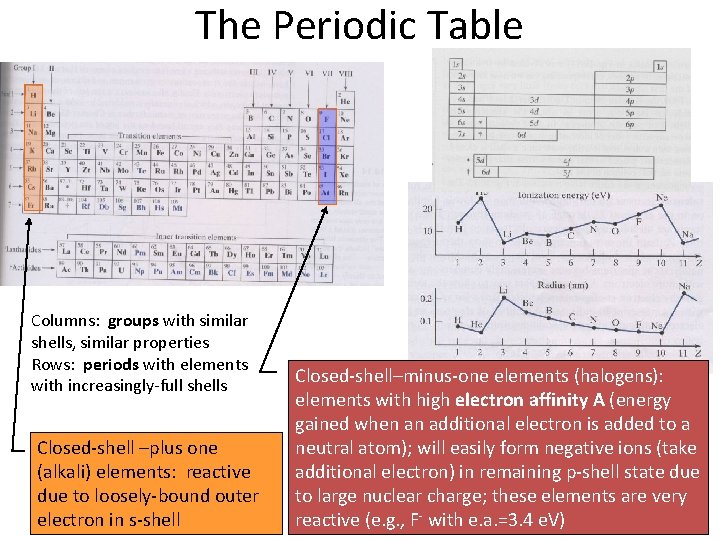
The Periodic Table Columns: groups with similar shells, similar properties Rows: periods with elements with increasingly-full shells Closed-shell –plus one (alkali) elements: reactive due to loosely-bound outer electron in s-shell Closed-shell–minus-one elements (halogens): elements with high electron affinity A (energy gained when an additional electron is added to a neutral atom); will easily form negative ions (take additional electron) in remaining p-shell state due to large nuclear charge; these elements are very reactive (e. g. , F- with e. a. =3. 4 e. V)

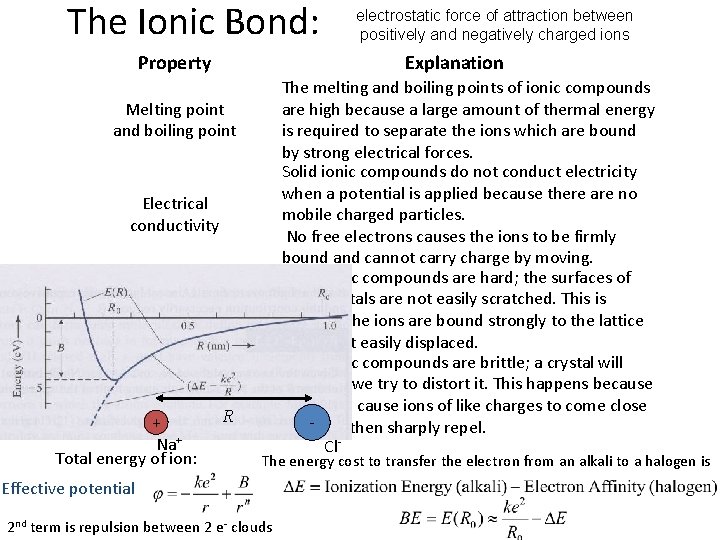
The Ionic Bond: Property Explanation Melting point and boiling point Electrical conductivity Hardness Brittleness + Na+ Total energy of ion: electrostatic force of attraction between positively and negatively charged ions R The melting and boiling points of ionic compounds are high because a large amount of thermal energy is required to separate the ions which are bound by strong electrical forces. Solid ionic compounds do not conduct electricity when a potential is applied because there are no mobile charged particles. No free electrons causes the ions to be firmly bound and cannot carry charge by moving. Most ionic compounds are hard; the surfaces of their crystals are not easily scratched. This is because the ions are bound strongly to the lattice and aren't easily displaced. Most ionic compounds are brittle; a crystal will shatter if we try to distort it. This happens because distortion cause ions of like charges to come close together then sharply repel. Cl The energy cost to transfer the electron from an alkali to a halogen is Effective potential 2 nd term is repulsion between 2 e- clouds

e. g. : F 2, HF • • The Covalent Bond The covalent bond is formed by sharing of outer shell electrons between atoms rather than by electron transfer. This lowers the energy of the system since electrons are attracted to both nuclei (stronger effective Coulomb potential) As an example, consider the H 2+ molecular ion (two protons, one e-): As the distance between the atoms is decreased, significant interference between the wave functions occur • In the bonding (symmetric) y+ state electron has a larger probability of being attracted by both protons – this state is the one responsible for the molecule formation. Therefore, the bonding state has a lower energy than the antibonding (antisymmetric). •

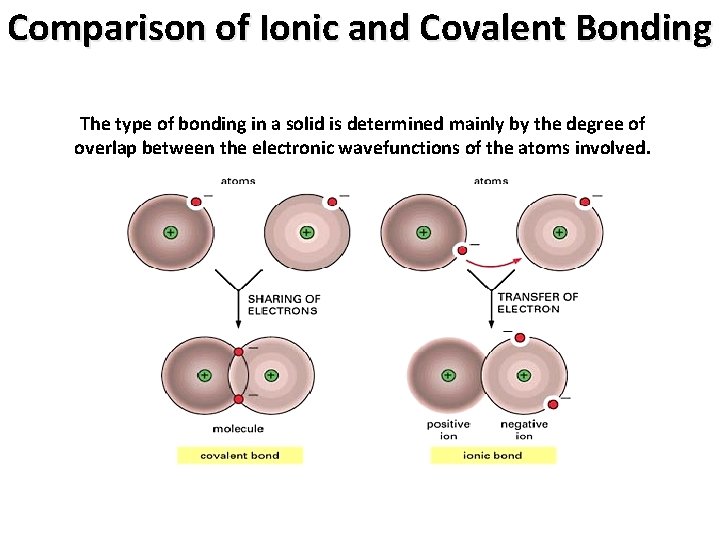
Comparison of Ionic and Covalent Bonding The type of bonding in a solid is determined mainly by the degree of overlap between the electronic wavefunctions of the atoms involved.

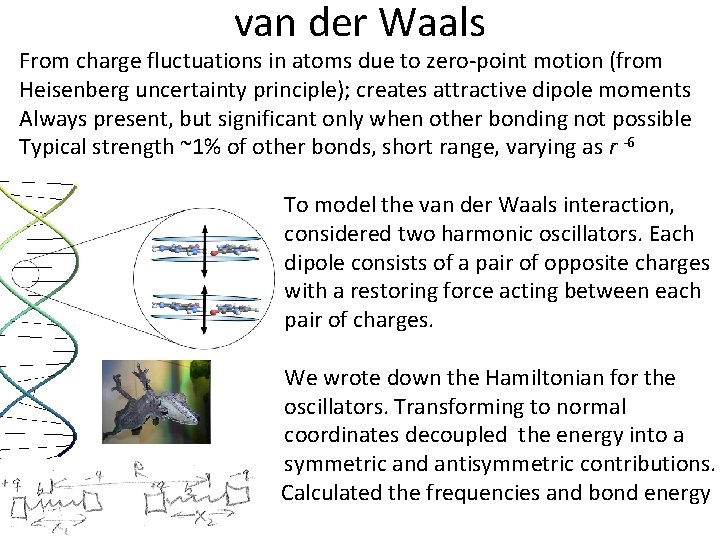
van der Waals From charge fluctuations in atoms due to zero-point motion (from Heisenberg uncertainty principle); creates attractive dipole moments Always present, but significant only when other bonding not possible Typical strength ~1% of other bonds, short range, varying as r -6 To model the van der Waals interaction, considered two harmonic oscillators. Each dipole consists of a pair of opposite charges with a restoring force acting between each pair of charges. We wrote down the Hamiltonian for the oscillators. Transforming to normal coordinates decoupled the energy into a symmetric and antisymmetric contributions. Calculated the frequencies and bond energy

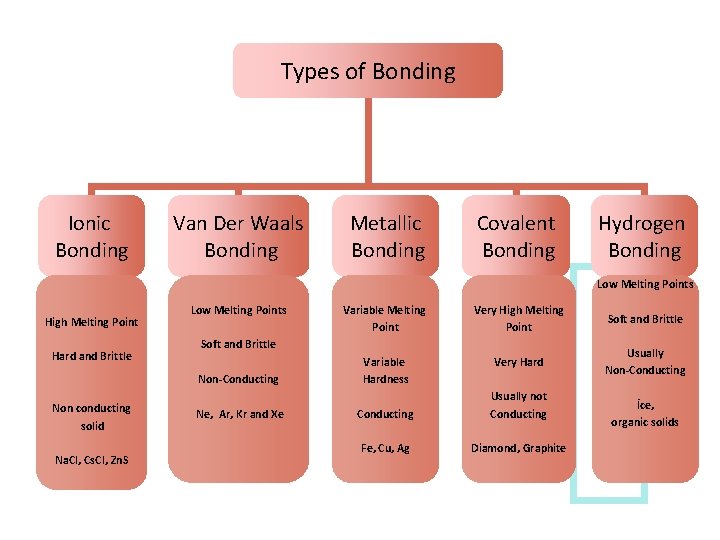
Types of Bonding Ionic Bonding Van Der Waals Bonding Metallic Bonding Covalent Bonding Hydrogen Bonding Low Melting Points High Melting Point Hard and Brittle Low Melting Points Na. Cl, Cs. Cl, Zn. S Very High Melting Point Soft and Brittle Variable Hardness Very Hard Usually Non-Conducting Soft and Brittle Non-Conducting Non conducting solid Variable Melting Point Ne, Ar, Kr and Xe Conducting Usually not Conducting Fe, Cu, Ag Diamond, Graphite İce, organic solids

C 2: Translational Lattice Vectors – 2 D A lattice is a set of points such that a translation from any point in the lattice by a vector; P R n = n 1 a + n 2 b locates an exactly equivalent point, i. e. a point with the same environment as P. This is translational symmetry. Point D (n 1, n 2) = (0, 2) Point F (n 1, n 2) = (0, -1) Point P (n 1, n 2) = (3, 2) The vectors a, b are known as lattice vectors and (n 1, n 2) is a pair of integers whose values depend on the lattice point.

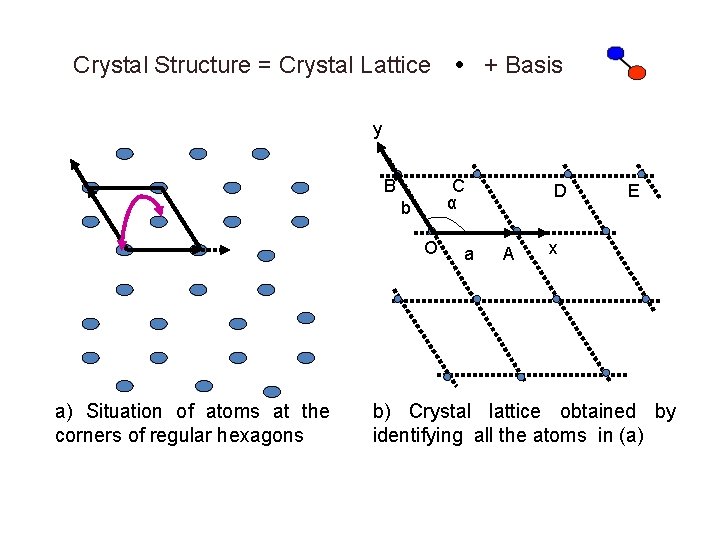
Crystal Structure = Crystal Lattice + Basis y B C α b O a) Situation of atoms at the corners of regular hexagons a D A E x b) Crystal lattice obtained by identifying all the atoms in (a)

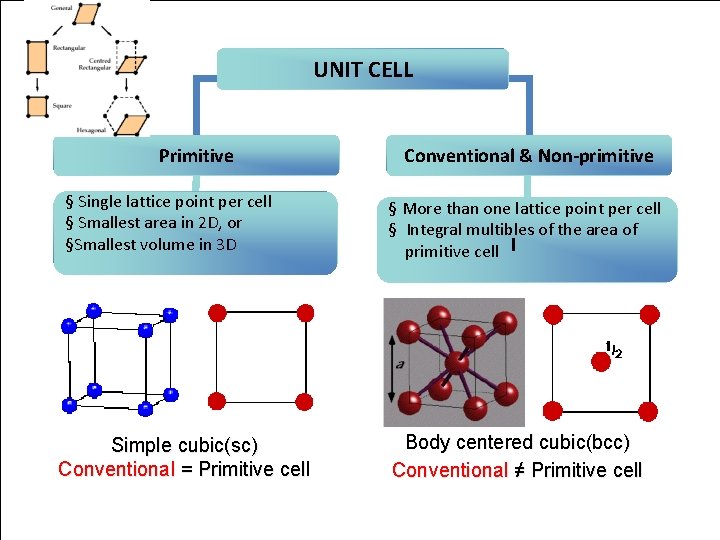
UNIT CELL Primitive § Single lattice point per cell § Smallest area in 2 D, or §Smallest volume in 3 D Simple cubic(sc) Conventional = Primitive cell Conventional & Non-primitive § More than one lattice point per cell § Integral multibles of the area of primitive cell Body centered cubic(bcc) Conventional ≠ Primitive cell Crystal Structure 10

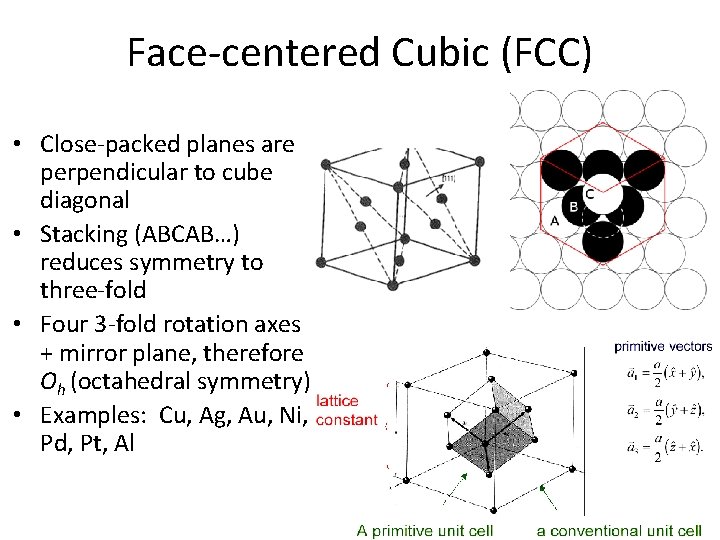
Face-centered Cubic (FCC) • Close-packed planes are perpendicular to cube diagonal • Stacking (ABCAB…) reduces symmetry to three-fold • Four 3 -fold rotation axes + mirror plane, therefore Oh (octahedral symmetry) • Examples: Cu, Ag, Au, Ni, Pd, Pt, Al

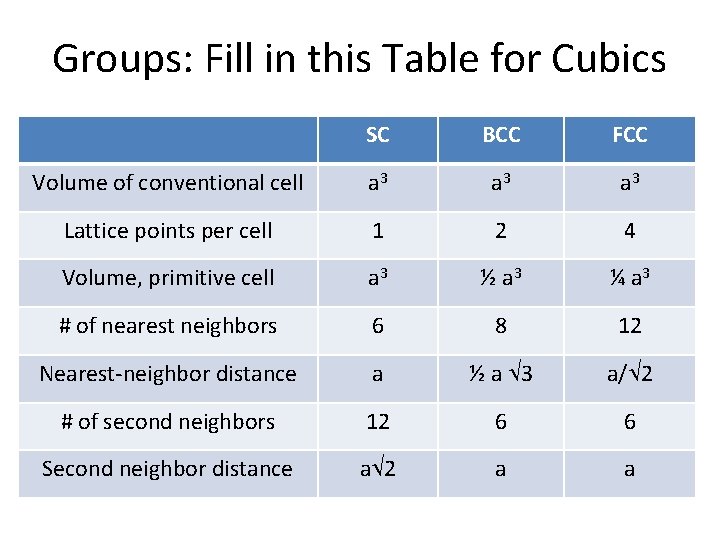
Groups: Fill in this Table for Cubics SC BCC FCC Volume of conventional cell a 3 a 3 Lattice points per cell 1 2 4 Volume, primitive cell a 3 ½ a 3 ¼ a 3 # of nearest neighbors 6 8 12 Nearest-neighbor distance a ½ a 3 a/ 2 # of second neighbors 12 6 6 Second neighbor distance a 2 a a

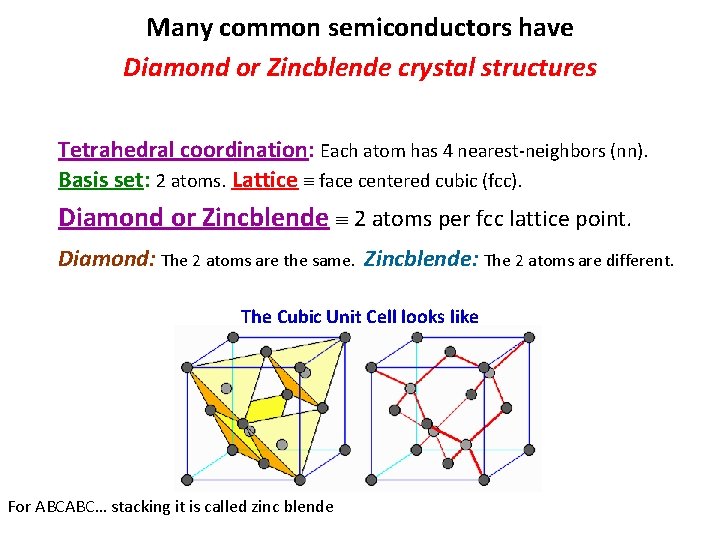
Many common semiconductors have Diamond or Zincblende crystal structures Tetrahedral coordination: Each atom has 4 nearest-neighbors (nn). Basis set: 2 atoms. Lattice face centered cubic (fcc). Diamond or Zincblende 2 atoms per fcc lattice point. Diamond: The 2 atoms are the same. Zincblende: The 2 atoms are different. The Cubic Unit Cell looks like For ABCABC… stacking it is called zinc blende

Group: Cs. Cl • The figure shows the crystal structure of Cs. Cl. Take the lattice constant as a, all the bonds shown have the same length. The grey atoms are Cs and the green ones are Cl. • What are the primitive Bravais lattice and the associated basis for this crystal (including the locations of these atoms in terms of lattice parameter a)? • What is the distance to the nearest neighbors of Cs?

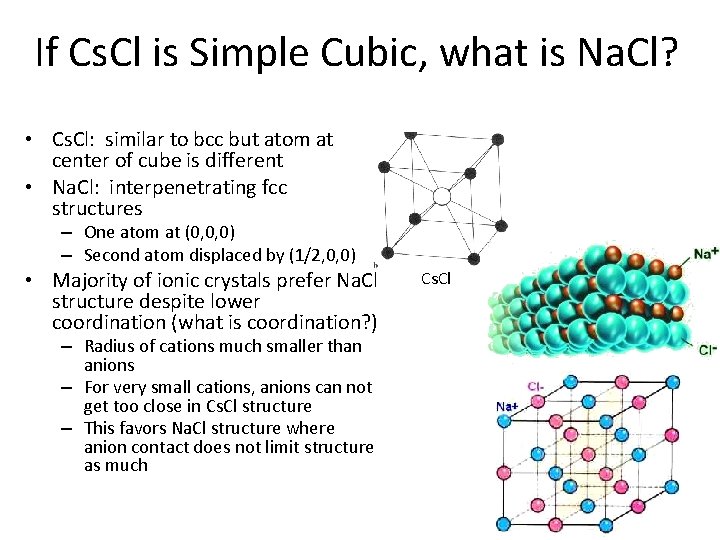
If Cs. Cl is Simple Cubic, what is Na. Cl? • Cs. Cl: similar to bcc but atom at center of cube is different • Na. Cl: interpenetrating fcc structures – One atom at (0, 0, 0) – Second atom displaced by (1/2, 0, 0) • Majority of ionic crystals prefer Na. Cl structure despite lower coordination (what is coordination? ) – Radius of cations much smaller than anions – For very small cations, anions can not get too close in Cs. Cl structure – This favors Na. Cl structure where anion contact does not limit structure as much Cs. Cl Na. Cl

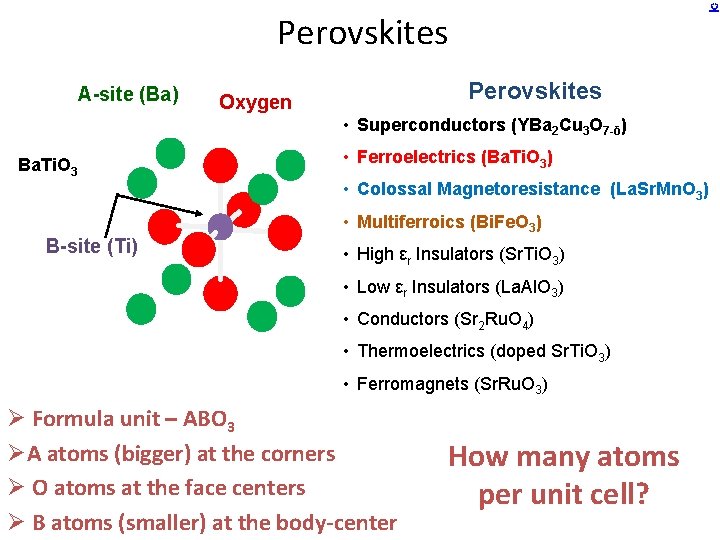
Perovskites A-site (Ba) Perovskites Oxygen • Superconductors (YBa 2 Cu 3 O 7 -δ) Ba. Ti. O 3 • Ferroelectrics (Ba. Ti. O 3) • Colossal Magnetoresistance (La. Sr. Mn. O 3) B-site (Ti) • Multiferroics (Bi. Fe. O 3) • High εr Insulators (Sr. Ti. O 3) • Low εr Insulators (La. Al. O 3) • Conductors (Sr 2 Ru. O 4) • Thermoelectrics (doped Sr. Ti. O 3) • Ferromagnets (Sr. Ru. O 3) Ø Formula unit – ABO 3 ØA atoms (bigger) at the corners Ø O atoms at the face centers Ø B atoms (smaller) at the body-center How many atoms per unit cell?

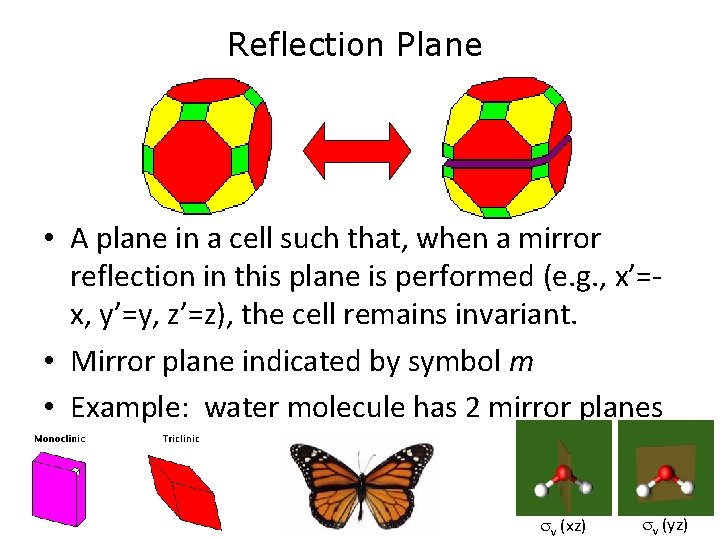
Reflection Plane • A plane in a cell such that, when a mirror reflection in this plane is performed (e. g. , x’=x, y’=y, z’=z), the cell remains invariant. • Mirror plane indicated by symbol m • Example: water molecule has 2 mirror planes v (xz) v (yz)

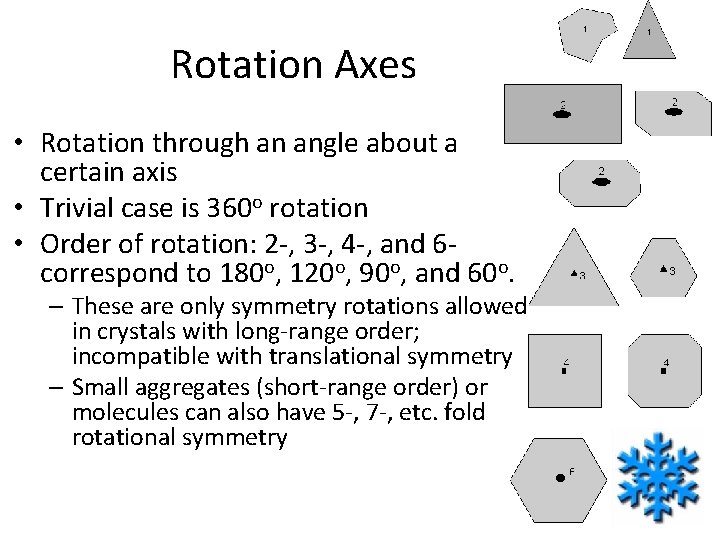
Rotation Axes • Rotation through an angle about a certain axis • Trivial case is 360 o rotation • Order of rotation: 2 -, 3 -, 4 -, and 6 correspond to 180 o, 120 o, 90 o, and 60 o. – These are only symmetry rotations allowed in crystals with long-range order; incompatible with translational symmetry – Small aggregates (short-range order) or molecules can also have 5 -, 7 -, etc. fold rotational symmetry

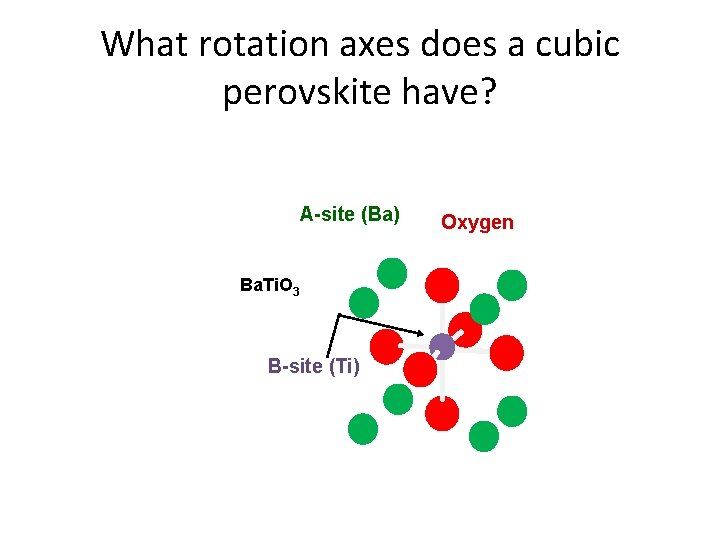
What rotation axes does a cubic perovskite have? A-site (Ba) Ba. Ti. O 3 B-site (Ti) Oxygen

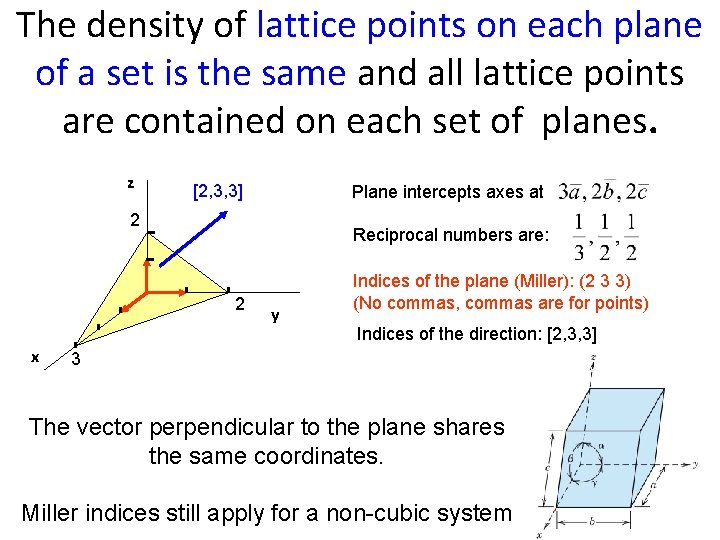
The density of lattice points on each plane of a set is the same and all lattice points are contained on each set of planes. z [2, 3, 3] Plane intercepts axes at 2 Reciprocal numbers are: 2 x y Indices of the plane (Miller): (2 3 3) (No commas, commas are for points) Indices of the direction: [2, 3, 3] 3 The vector perpendicular to the plane shares the same coordinates. Miller indices still apply for a non-cubic system

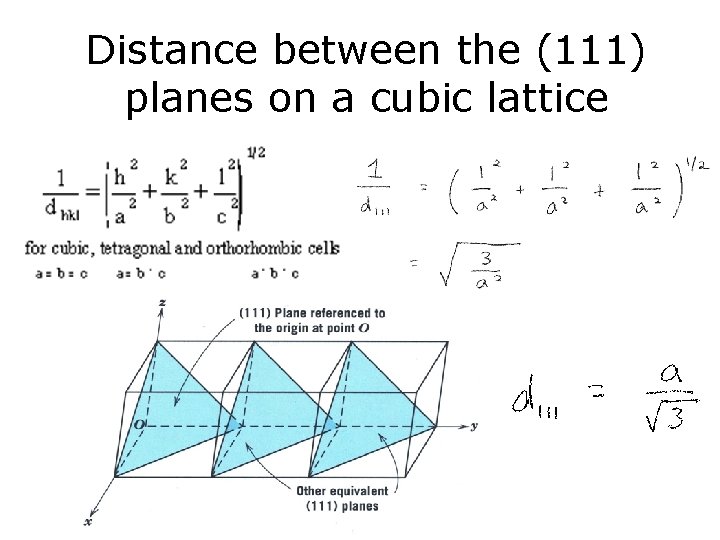
Distance between the (111) planes on a cubic lattice

Review: Reciprocal Lattice The reciprocal lattice is composed of all points lying at positions from the origin, so that there is one point in the reciprocal lattice for each set of planes (hkl) in the real-space lattice. Suppose G can be decomposed into basis vectors: (h, k, l integers) Note: a has dimensions of length, g has dimensions of length-1 Ghkl is perpendicular to (hkl) plane The basis vectors gi define a reciprocal lattice: 1. for every real lattice there’s a reciprocal lattice 2. reciprocal lattice vector g 1 is perpendicular to plane defined by a 2 and a 3 + cyclic permutations is volume of unit cell a’s are not unique, but volume is

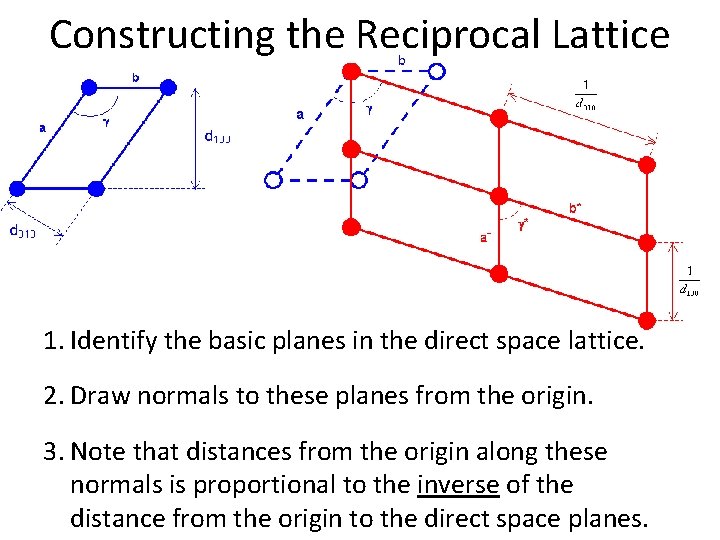
Constructing the Reciprocal Lattice 1. Identify the basic planes in the direct space lattice. 2. Draw normals to these planes from the origin. 3. Note that distances from the origin along these normals is proportional to the inverse of the distance from the origin to the direct space planes.

Reciprocal Lattices to SC, FCC and BCC Direct lattice SC BCC FCC Reciprocal lattice Volume of RL Direct Reciprocal Simple cubic bcc fcc bcc

DIFFRACTION • Diffraction is a wave phenomenon in which the apparent bending and spreading of waves when they meet an obstruction is measured. • Light, radio, sound and water waves. • Diffraction is optimally sensitive to the periodic nature of the solid’s atomic structure. Width Variable (500 -1500 nm) Wavelength Constant (600 nm) Distance d = Constant

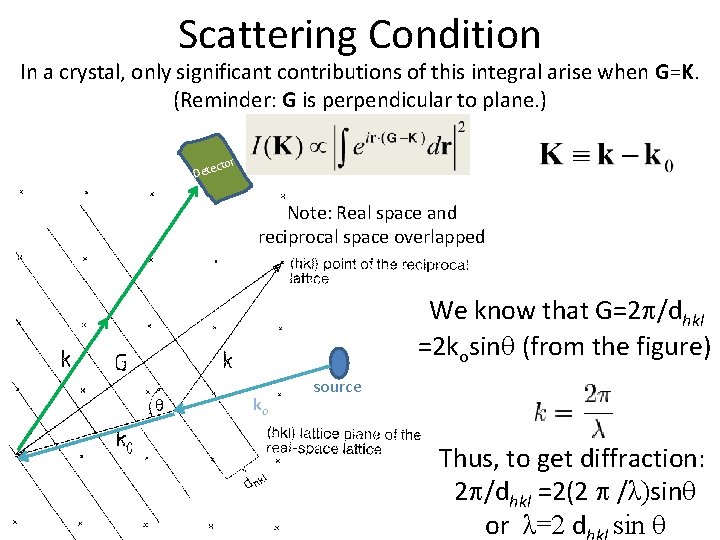
Scattering Condition In a crystal, only significant contributions of this integral arise when G=K. (Reminder: G is perpendicular to plane. ) Dete ctor Note: Real space and reciprocal space overlapped We know that G=2 /dhkl =2 kosin (from the figure) ko source Thus, to get diffraction: 2 /dhkl =2(2 /λ)sin or λ=2 d sin

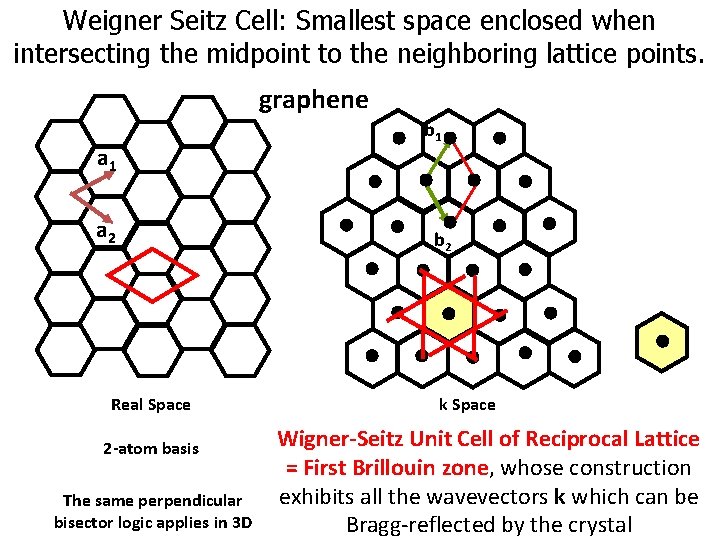
Weigner Seitz Cell: Smallest space enclosed when intersecting the midpoint to the neighboring lattice points. graphene a 1 a 2 Real Space 2 -atom basis The same perpendicular bisector logic applies in 3 D b 1 b 2 k Space Wigner-Seitz Unit Cell of Reciprocal Lattice = First Brillouin zone, whose construction exhibits all the wavevectors k which can be Bragg-reflected by the crystal

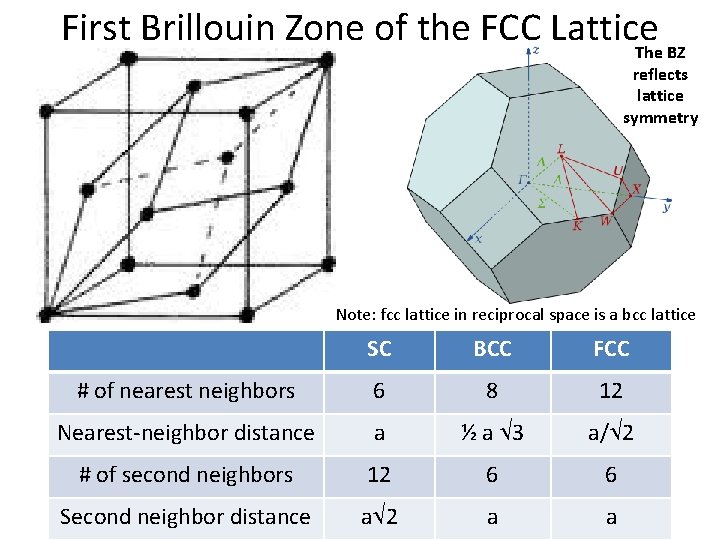
First Brillouin Zone of the FCC Lattice The BZ reflects lattice symmetry Note: fcc lattice in reciprocal space is a bcc lattice SC BCC FCC 6 8 12 Nearest-neighbor distance a ½ a 3 a/ 2 # of second neighbors 12 6 6 Second neighbor distance a 2 a a FCC Primitive and # of nearest Unit neighbors Conventional Cells

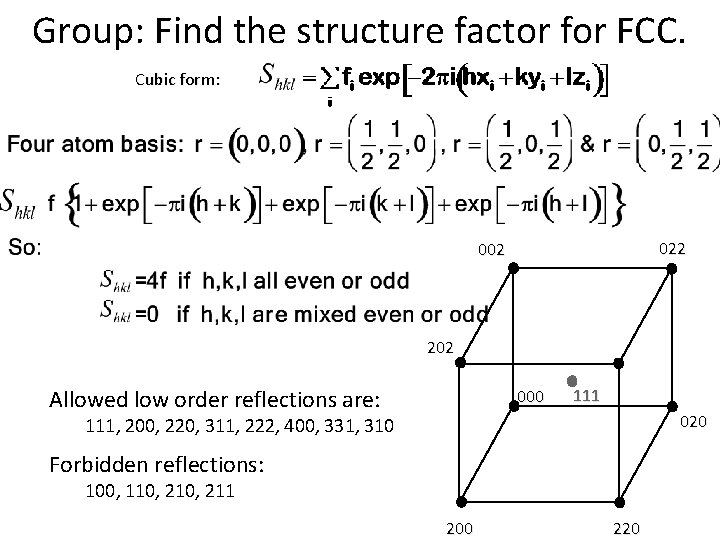
Group: Find the structure factor for FCC. Cubic form: 022 002 202 Allowed low order reflections are: 000 111 020 111, 200, 220, 311, 222, 400, 331, 310 Forbidden reflections: 100, 110, 211 200 220

Structure Factor Ni 3 Al (L 12) structure Simple cubic lattice, with a four atom basis Again, since simple cubic, intensity at all points. But each point is ‘chemically sensitive’.

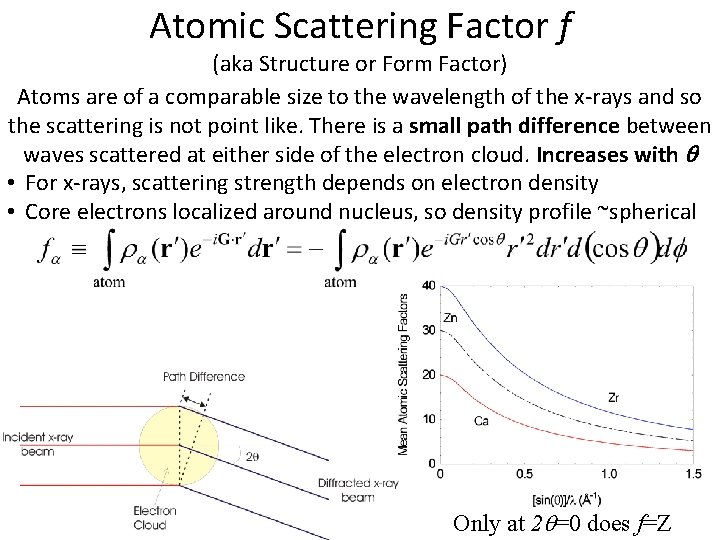
Atomic Scattering Factor f (aka Structure or Form Factor) Atoms are of a comparable size to the wavelength of the x-rays and so the scattering is not point like. There is a small path difference between waves scattered at either side of the electron cloud. Increases with • For x-rays, scattering strength depends on electron density • Core electrons localized around nucleus, so density profile ~spherical Only at 2 =0 does f=Z

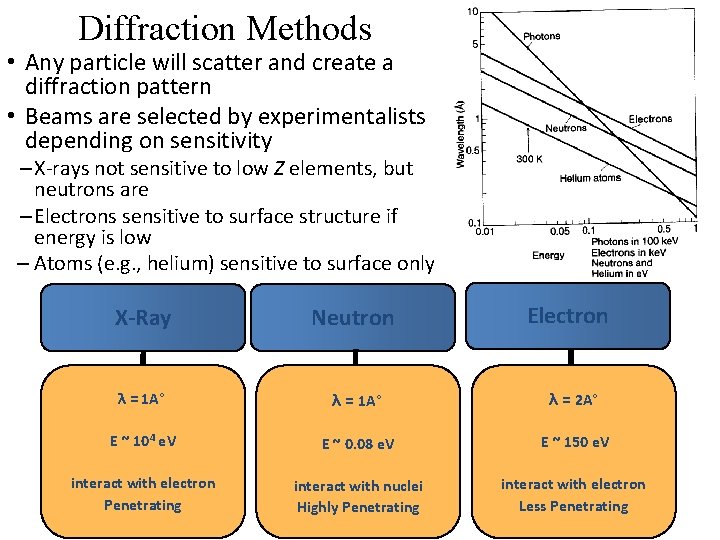
Diffraction Methods • Any particle will scatter and create a diffraction pattern • Beams are selected by experimentalists depending on sensitivity – X-rays not sensitive to low Z elements, but neutrons are – Electrons sensitive to surface structure if energy is low – Atoms (e. g. , helium) sensitive to surface only Electron X-Ray Neutron λ = 1 A° λ = 2 A° E ~ 104 e. V E ~ 0. 08 e. V E ~ 150 e. V interact with electron Penetrating interact with nuclei Highly Penetrating interact with electron Less Penetrating

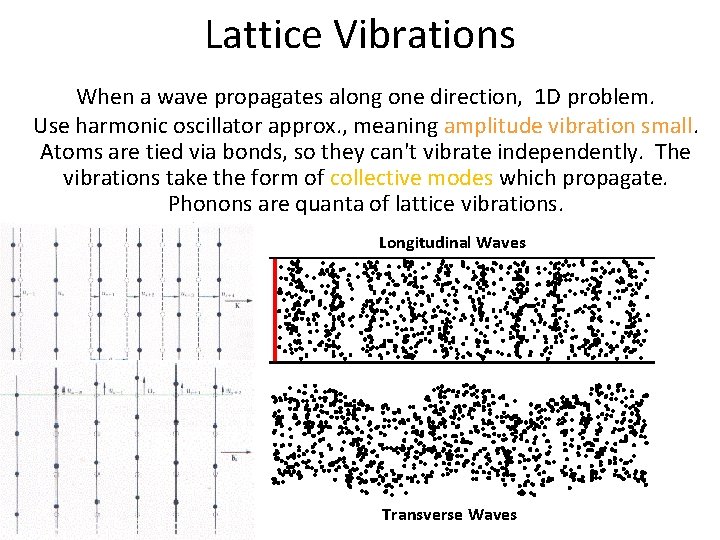
Lattice Vibrations When a wave propagates along one direction, 1 D problem. Use harmonic oscillator approx. , meaning amplitude vibration small. Atoms are tied via bonds, so they can't vibrate independently. The vibrations take the form of collective modes which propagate. Phonons are quanta of lattice vibrations. Longitudinal Waves Transverse Waves

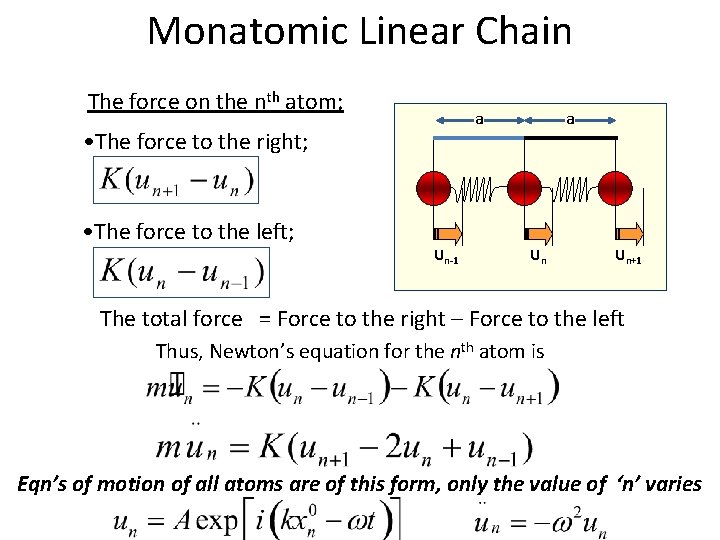
Monatomic Linear Chain The force on the nth atom; a • The force to the right; • The force to the left; Un-1 a Un Un+1 The total force = Force to the right – Force to the left Thus, Newton’s equation for the nth atom is Eqn’s of motion of all atoms are of this form, only the value of ‘n’ varies

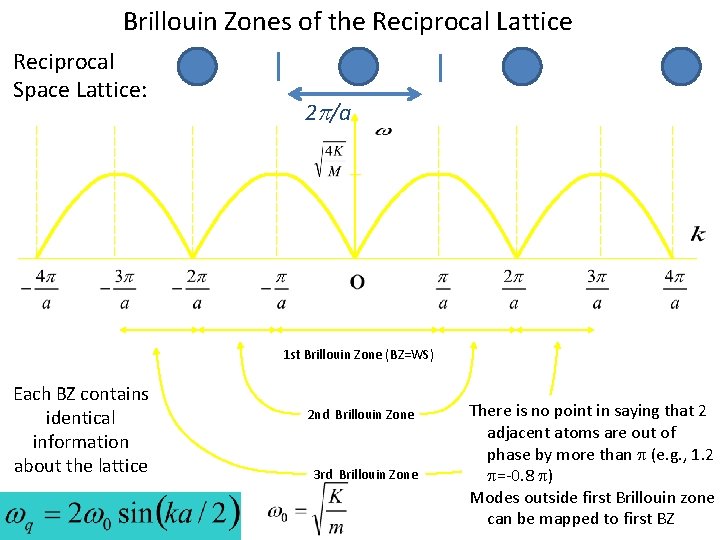
Brillouin Zones of the Reciprocal Lattice Reciprocal Space Lattice: 2 p/a 1 st Brillouin Zone (BZ=WS) Each BZ contains identical information about the lattice 2 nd Brillouin Zone 3 rd Brillouin Zone There is no point in saying that 2 adjacent atoms are out of phase by more than (e. g. , 1. 2 =-0. 8 ) Modes outside first Brillouin zone can be mapped to first BZ

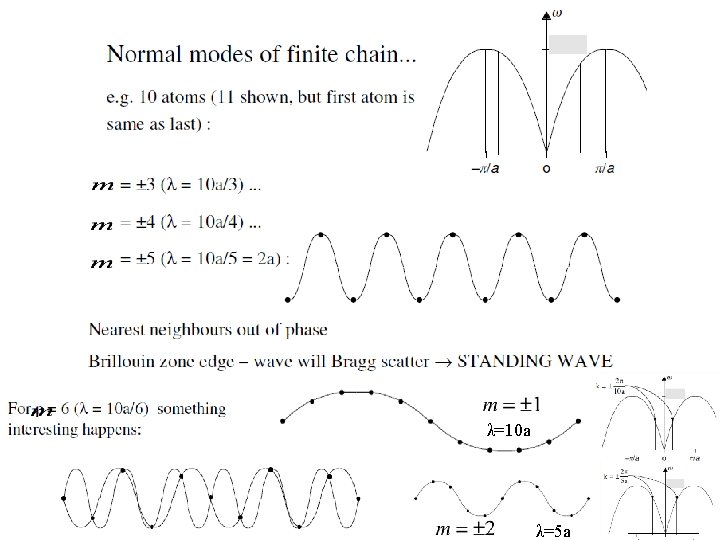
λ=10 a λ=5 a

Wave velocity • GROUP VELOCITY is velocity of energy transfer • If vphase > vgroup, wave is dispersive • vphase= k/k • The slope of the dispersion curve gives the group velocity. • Near the origin k = 0 the phase and group velocity must be the same (dispersionless) • The edges of the FBZ correspond to neighboring atoms moving in opposite directions. The energy cannot propagate along the crystal. Standing wave at the boundaries of the BZ (λ=2 a)

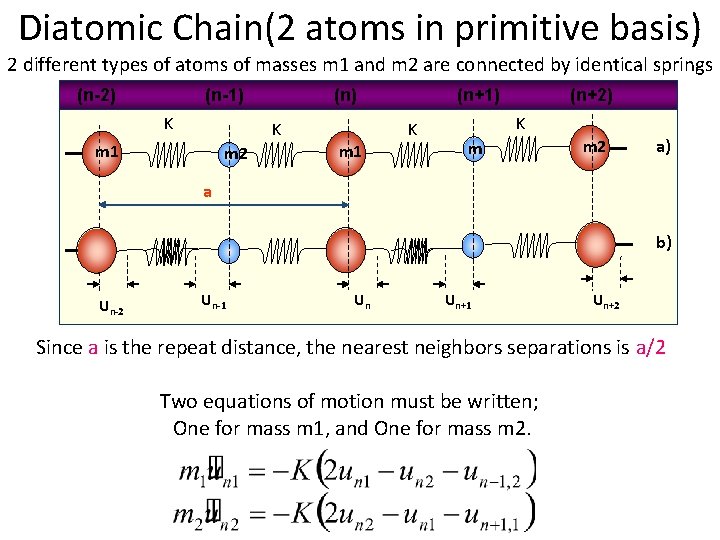
Diatomic Chain(2 atoms in primitive basis) 2 different types of atoms of masses m 1 and m 2 are connected by identical springs (n-2) (n-1) K (n) K m 1 m 2 (n+1) K m 1 (n+2) K m m 2 a) a b) Un-2 Un-1 Un Un+1 Un+2 Since a is the repeat distance, the nearest neighbors separations is a/2 Two equations of motion must be written; One for mass m 1, and One for mass m 2.

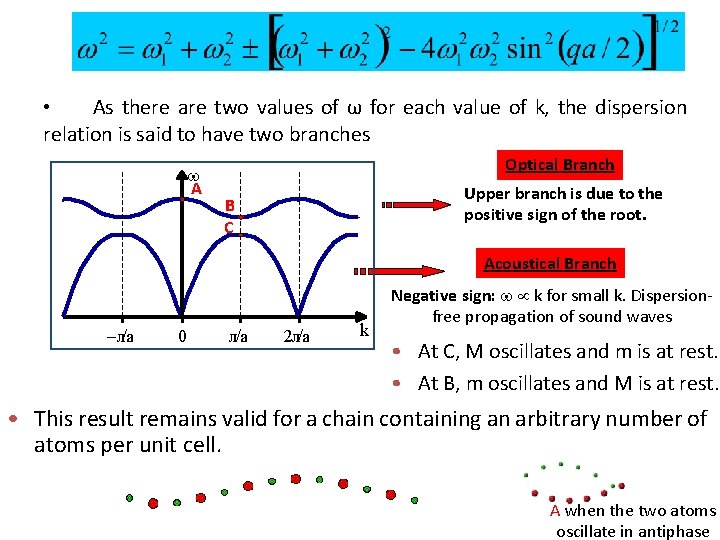
• As there are two values of ω for each value of k, the dispersion relation is said to have two branches A Optical Branch Upper branch is due to the positive sign of the root. B C Acoustical Branch –л/a 0 л/a 2 л/a k Negative sign: k for small k. Dispersionfree propagation of sound waves • At C, M oscillates and m is at rest. • At B, m oscillates and M is at rest. • This result remains valid for a chain containing an arbitrary number of atoms per unit cell. A when the two atoms oscillate in antiphase

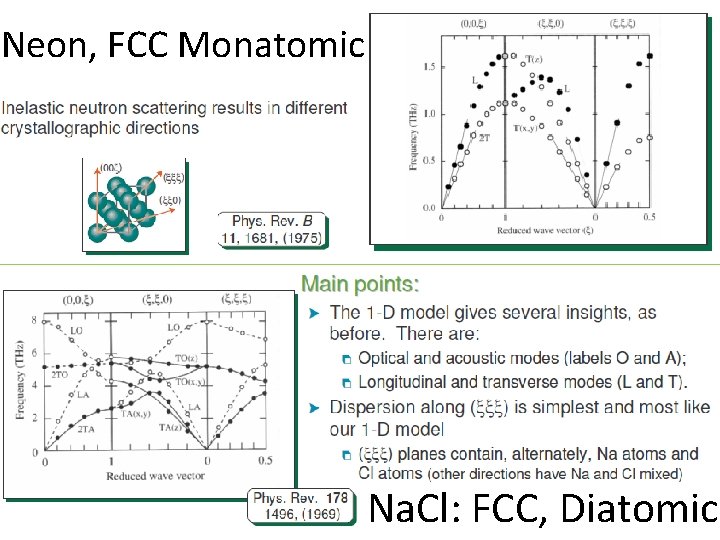
Neon, FCC Monatomic Na. Cl: FCC, Diatomic

3 D Dispersion curves • Every crystal has 3 acoustic branches, 1 longitudinal and 2 transverse • Every additional atom in the primitive basis contributes 3 further optical branches (again 2 transverse and 1 longitudinal) • P atoms/primitive unit cell means 3 acoustic branches and 3(p-1) optical branches=3 p branches • One for each degree of freedom

Stress Tensor Forces divided by an area are called stresses. The stresses/tractions tk (or k) along axis k are. . . in components we can write this as where ij is the stress tensor and nj is a surface normal. The stress tensor describes the forces acting on planes within a body. Due to the symmetry condition there are only six independent elements. The vector normal to the corresponding surface The direction of the force vector acting on that surface

We can therefore write: Similarly, the strain tensor can be written as: Additional simplification of the stress-strain relationship can be realized through simplifying the matrix notation for stresses and strains. We can replace the indices as follows: Voigt’s notation:

• For the generalized case, Hooke’s law may be expressed as: where, • Both Sijkl and Cijkl are fourth-rank tensor quantities. • The consequence of the symmetry in the stress and strain tensors is that only 36 components of the compliance and stiffness tensors are independent and distinct terms. But only one-half of the non-diagonal terms are independent constants since Cij = Cji Independent terms

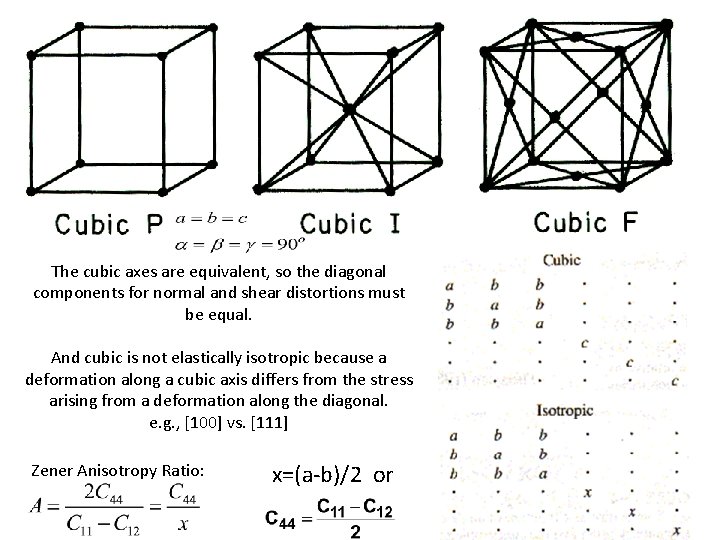
The cubic axes are equivalent, so the diagonal components for normal and shear distortions must be equal. And cubic is not elastically isotropic because a deformation along a cubic axis differs from the stress arising from a deformation along the diagonal. e. g. , [100] vs. [111] Zener Anisotropy Ratio: x=(a-b)/2 or

• These quantized normal modes of vibration are called PHONONS • PHONONS are massless quantum mechanical particles which have no classical analogue. – They behave like particles in momentum space or k space. • Phonons are one example of many like this in many different areas of physics. Such quantum mechanical particles are often called “Quasiparticles” Examples of other Quasiparticles: Photons: Quantized Normal Modes of electromagnetic waves. Magnons: Quantized Normal Modes of magnetic excitations in magnetic solids Excitons: Quantized Normal Modes of electron-hole pairs Polaritons: Quantized Normal Modes of electric polarization excitations in solids + Many Others!!!

Phonon spectroscopy = Conditions for: inelastic scattering Constraints: Conservation laws of Momentum Energy In all interactions involving phonons, energy must be conserved and crystal momentum must be conserved to within a reciprocal lattice vector.