The importance of visualization 12 V 1 0

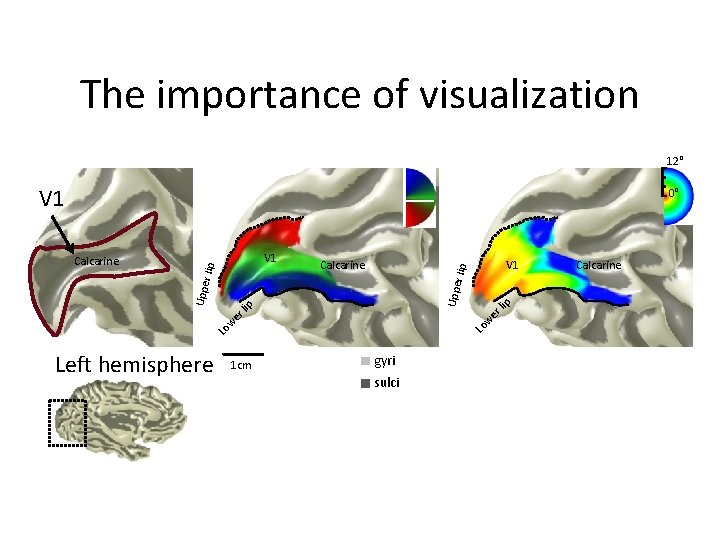
The importance of visualization 12° V 1 0° 1 cm ip rl ip we rl Lo we Lo Left hemisphere V 1 r lip Calcarine Uppe r lip V 1 Uppe Calcarine gyri sulci Calcarine

The importance of visualization • Precision • Understanding, understanding

Visualization should offer precise communication Why precision? (a) (b)

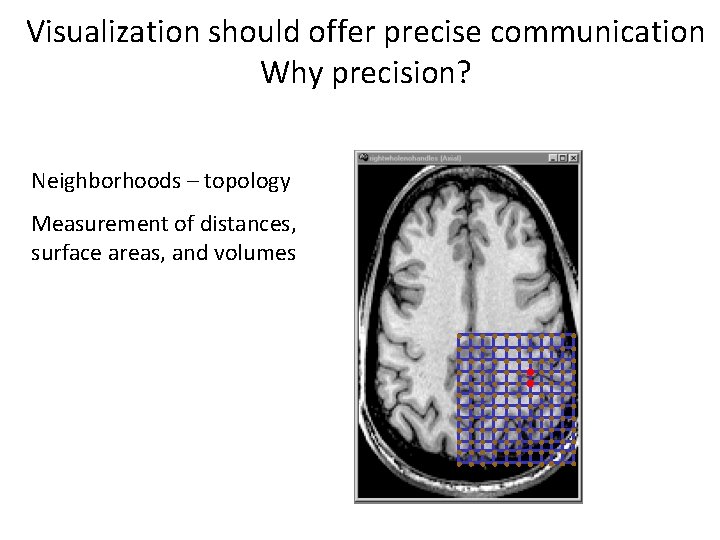
Visualization should offer precise communication Why precision? Neighborhoods – topology Measurement of distances, surface areas, and volumes

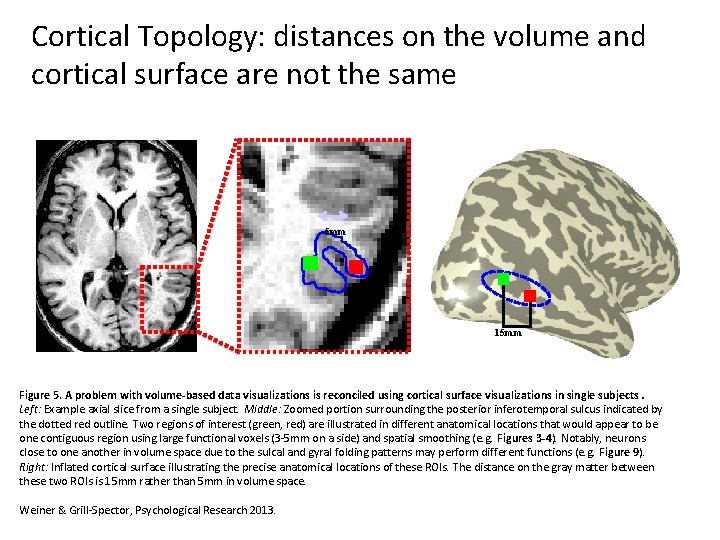
Cortical Topology: distances on the volume and cortical surface are not the same 5 mm 15 mm Figure 5. A problem with volume-based data visualizations is reconciled using cortical surface visualizations in single subjects. Left: Example axial slice from a single subject. Middle: Zoomed portion surrounding the posterior inferotemporal sulcus indicated by the dotted red outline. Two regions of interest (green, red) are illustrated in different anatomical locations that would appear to be one contiguous region using large functional voxels (3 -5 mm on a side) and spatial smoothing (e. g. Figures 3 -4). Notably, neurons close to one another in volume space due to the sulcal and gyral folding patterns may perform different functions (e. g. Figure 9). Right: Inflated cortical surface illustrating the precise anatomical locations of these ROIs. The distance on the gray matter between these two ROIs is 15 mm rather than 5 mm in volume space. Weiner & Grill-Spector, Psychological Research 2013.

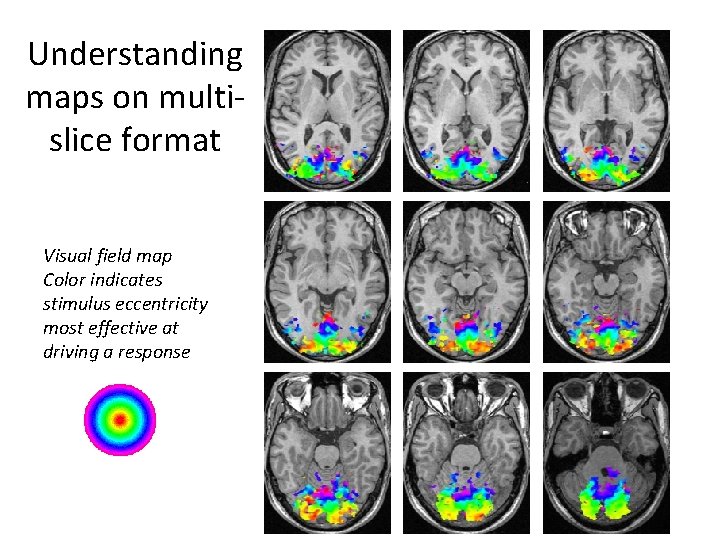
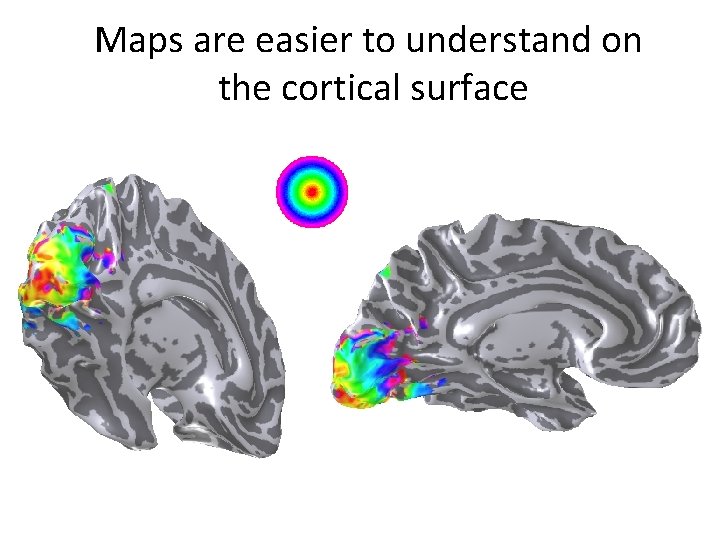
Understanding maps on multislice format Visual field map Color indicates stimulus eccentricity most effective at driving a response

Maps are easier to understand on the cortical surface

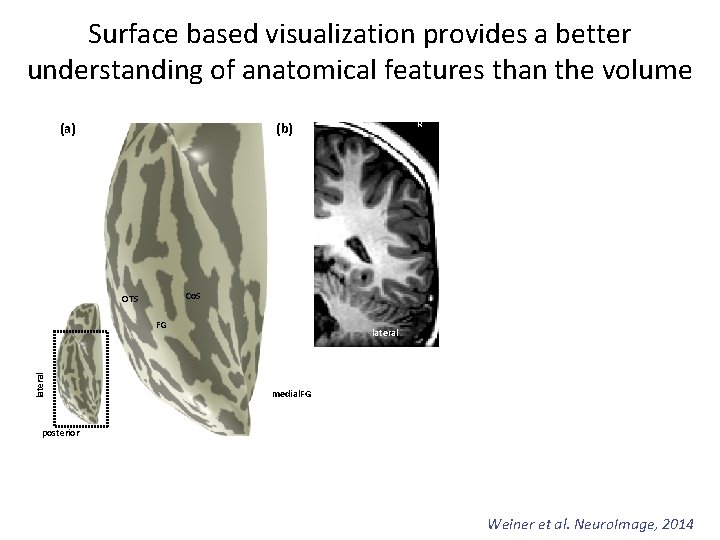
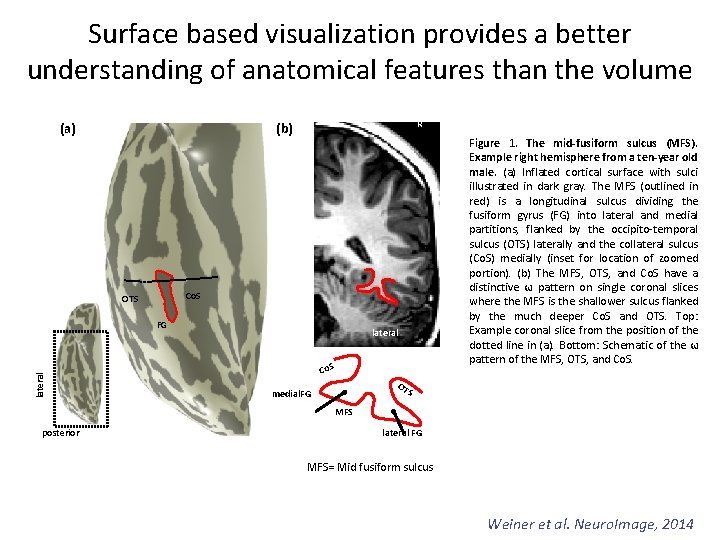
Surface based visualization provides a better understanding of anatomical features than the volume (a) Co. S OTS FG lateral R (b) lateral medial. FG posterior Weiner et al. Neuro. Image, 2014

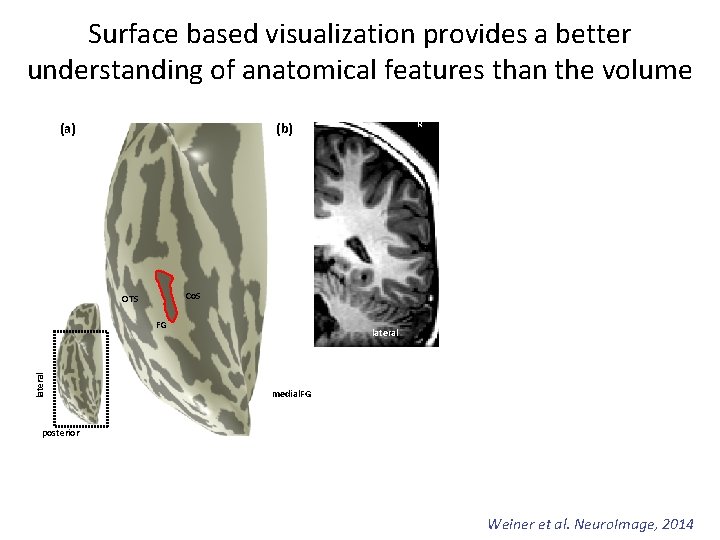
Surface based visualization provides a better understanding of anatomical features than the volume (a) Co. S OTS FG lateral R (b) lateral medial. FG posterior Weiner et al. Neuro. Image, 2014

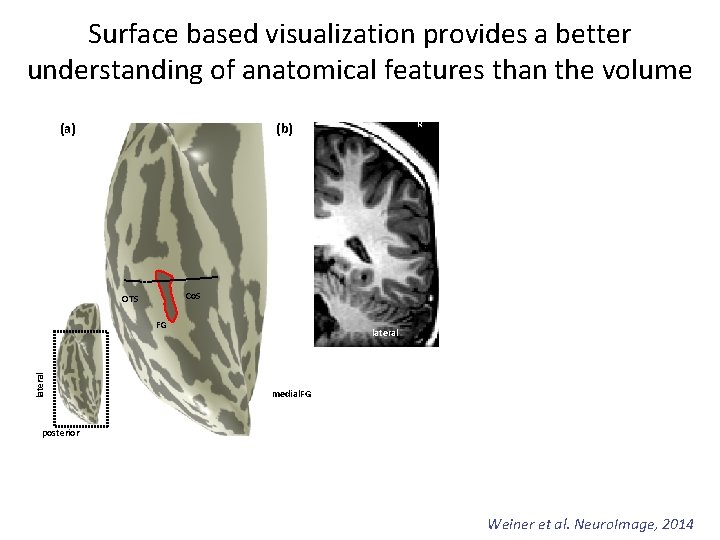
Surface based visualization provides a better understanding of anatomical features than the volume (a) Co. S OTS FG lateral R (b) lateral medial. FG posterior Weiner et al. Neuro. Image, 2014

Surface based visualization provides a better understanding of anatomical features than the volume (a) R (b) Co. S OTS FG lateral Figure 1. The mid-fusiform sulcus (MFS). Example right hemisphere from a ten-year old male. (a) Inflated cortical surface with sulci illustrated in dark gray. The MFS (outlined in red) is a longitudinal sulcus dividing the fusiform gyrus (FG) into lateral and medial partitions, flanked by the occipito-temporal sulcus (OTS) laterally and the collateral sulcus (Co. S) medially (inset for location of zoomed portion). (b) The MFS, OTS, and Co. S have a distinctive ω pattern on single coronal slices where the MFS is the shallower sulcus flanked by the much deeper Co. S and OTS. Top: Example coronal slice from the position of the dotted line in (a). Bottom: Schematic of the ω pattern of the MFS, OTS, and Co. S. lateral Co. S OT S medial. FG MFS posterior lateral FG MFS= Mid fusiform sulcus Weiner et al. Neuro. Image, 2014

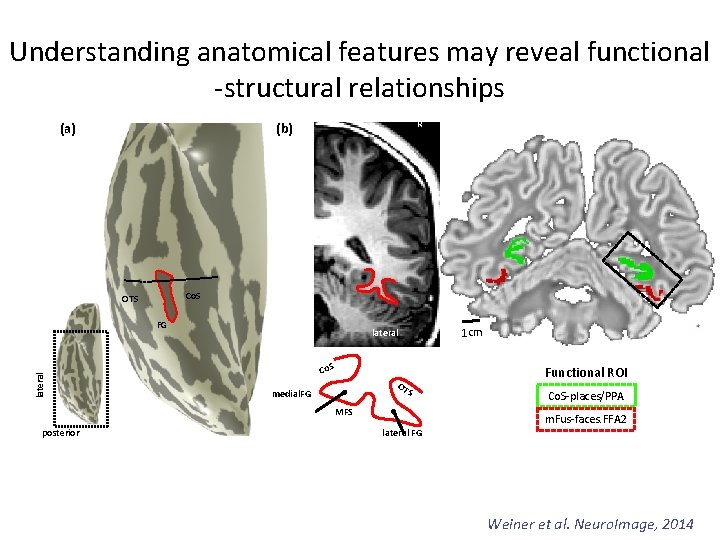
Understanding anatomical features may reveal functional -structural relationships (a) R (b) Co. S OTS lateral FG 1 cm lateral Co. S Functional ROI OT S medial. FG MFS posterior lateral FG Co. S-places/PPA m. Fus-faces. FFA 2 Weiner et al. Neuro. Image, 2014

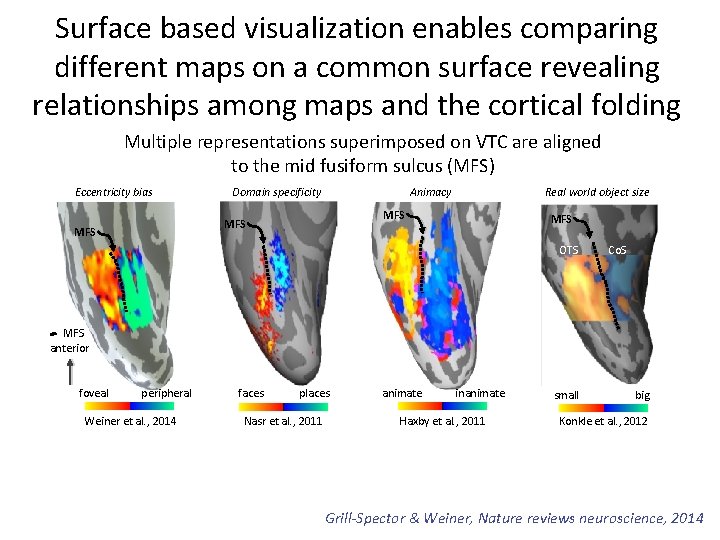
Surface based visualization enables comparing different maps on a common surface revealing relationships among maps and the cortical folding Multiple representations superimposed on VTC are aligned to the mid fusiform sulcus (MFS) Eccentricity bias Domain specificity Animacy MFS MFS Real world object size MFS OTS Co. S MFS anterior foveal peripheral Weiner et al. , 2014 faces places Nasr et al. , 2011 animate inanimate Haxby et al. , 2011 small big Konkle et al. , 2012 Grill-Spector & Weiner, Nature reviews neuroscience, 2014

Visualization techniques How to manual • Iso-voxel • Gray/white segmentation • Surface boundaries (Marching cubes) • Surface smoothing

(0. 9375, 1. 2) mm If the original scan did not obtain isotropic voxels

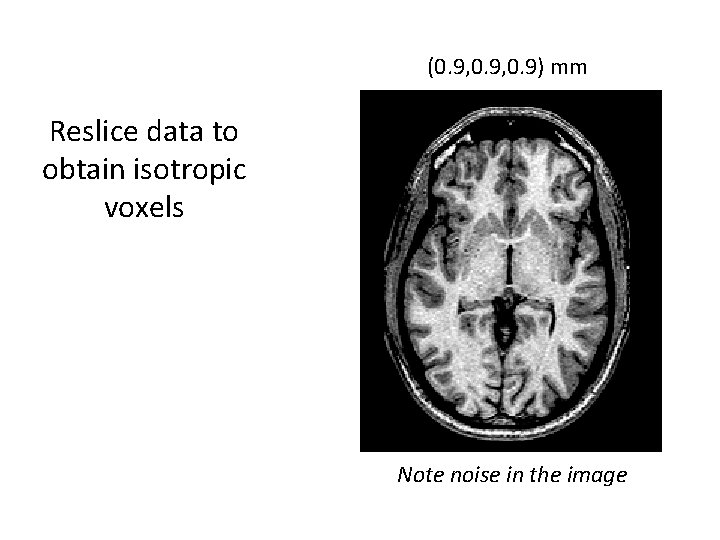
(0. 9, 0. 9) mm Reslice data to obtain isotropic voxels Note noise in the image

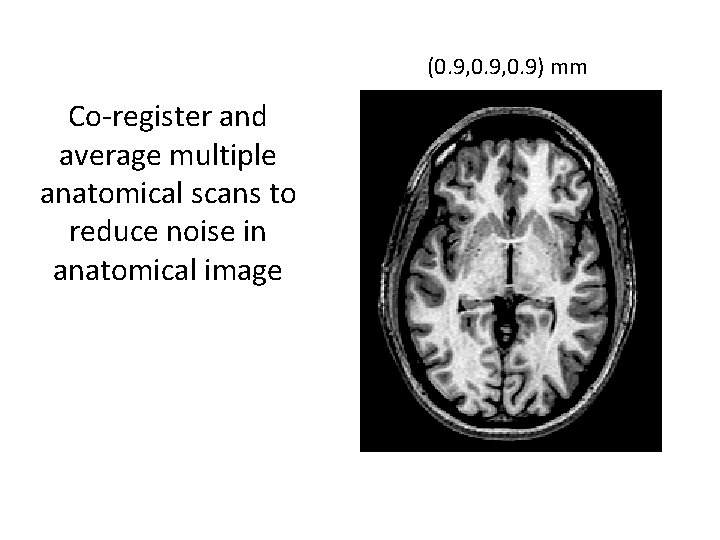
(0. 9, 0. 9) mm Co-register and average multiple anatomical scans to reduce noise in anatomical image

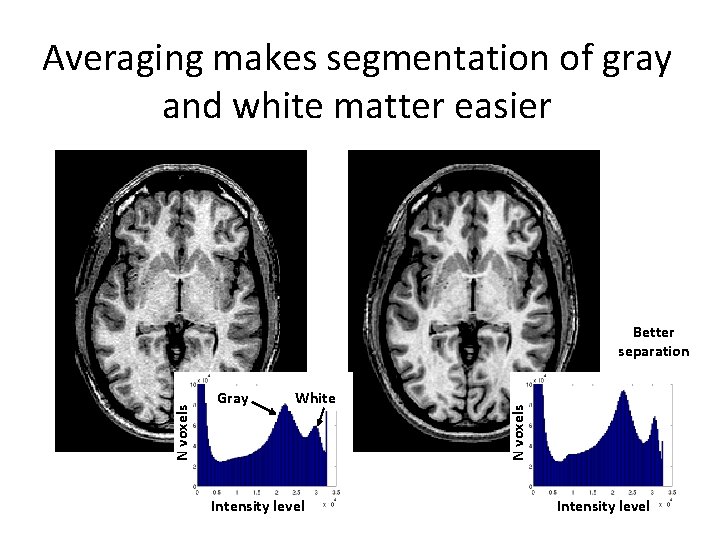
Averaging makes segmentation of gray and white matter easier Gray White Intensity level N voxels Better separation Intensity level

Visualization techniques How to manual • Iso-voxel • Segment brain into gray and white matter • Surface boundaries (Marching cubes) • Surface smoothing

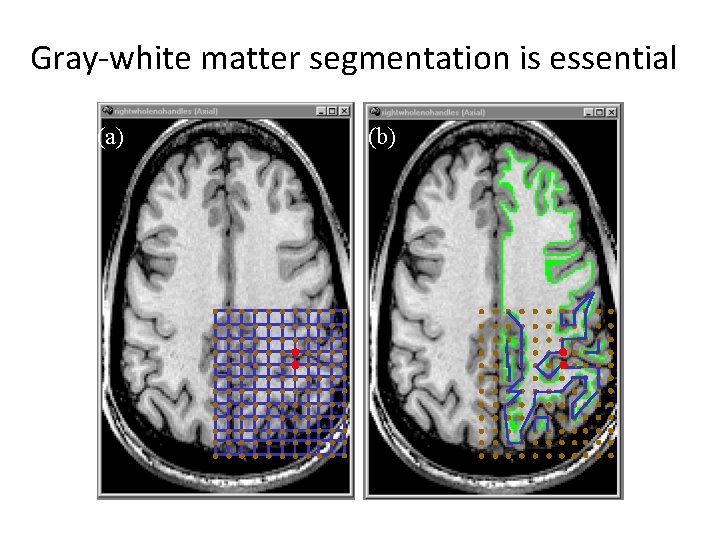
Gray-white matter segmentation is essential (a) (b)

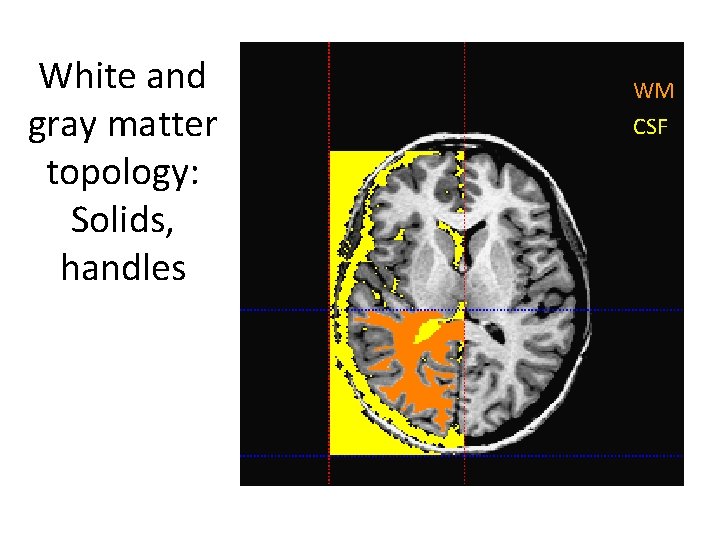
White and gray matter topology: Solids, handles WM CSF

White Matter Topology: Avoiding Cavities and Handles Cavity (hole) Handle • Euler number is a means of determining the presence of such imperfections • Algorithms for locating and replacing exist (Kriegeskorte and Goebel)

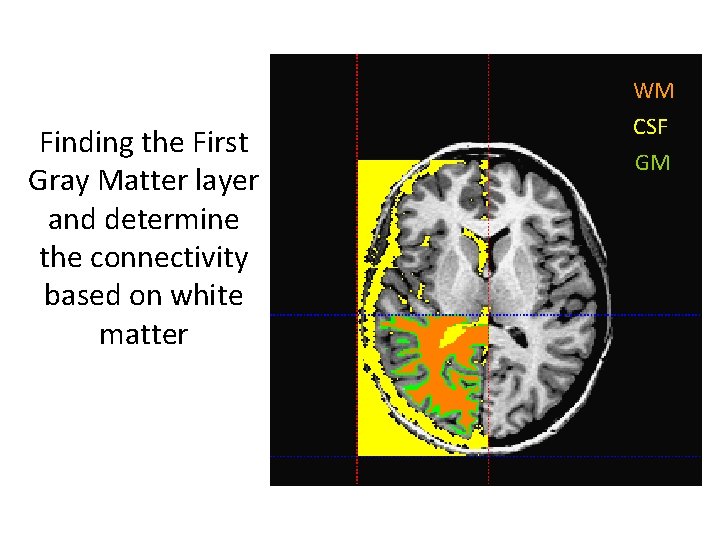
Finding the First Gray Matter layer and determine the connectivity based on white matter WM CSF GM

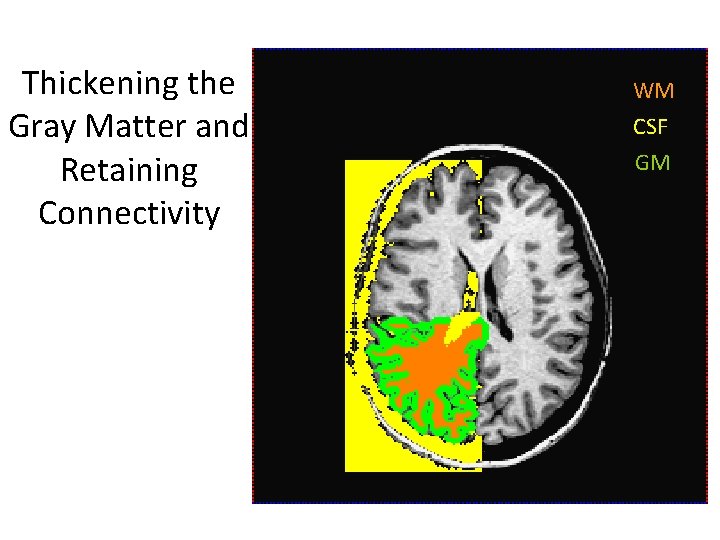
Thickening the Gray Matter and Retaining Connectivity WM CSF GM

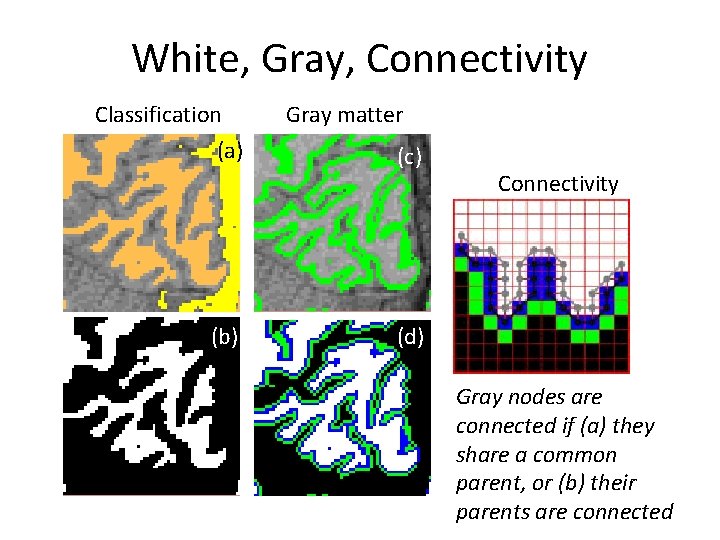
White, Gray, Connectivity Classification (a) (b) Gray matter (c) Connectivity (d) Gray nodes are connected if (a) they share a common parent, or (b) their parents are connected

The Importance of Being a Mesh From the white matter classification we create • A surface mesh for visualization • A gray node connection graph • Gray nodes are properly connected • No connections across sulci • Visualization simplified • Measurement of area and distance

Visualization techniques How to manual • Iso-voxel • Segment brain into gray and white matter • Determine the surface boundaries (Marching cubes algorithm) • Surface smoothing

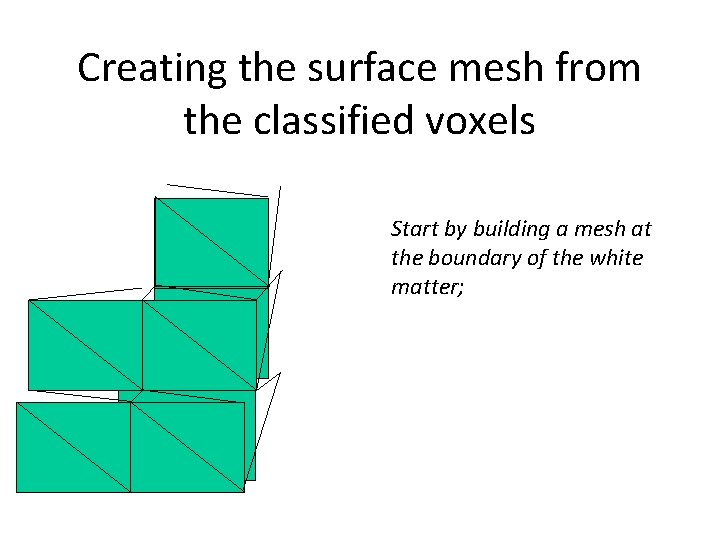
Creating the surface mesh from the classified voxels Start by building a mesh at the boundary of the white matter;

Surface boundary identification “Marching squares” Black: Shape Green: Inside vertices Red: New vertices. Draw boundary through these. There are basically only a few lines we can draw for the boundaries. The first step is to calculate the corners that are inside the shape (represented by the green dots). We can now insert some vertices, since we know which points are inside and which are outside we can guess that a vertex should be positioned approximately halfway between an inside corner and any outside corners that are connected by the edge of a cell. The diagram shows the discussed vertices as small red dots

Surface boundary identification “Marching squares” Black: Shape Green: Inside vertices Red: New vertices. Draw boundary through these. There are basically only a few lines we can draw for the boundaries. The diagram shows the matching surface formed by joining the vertices with lines

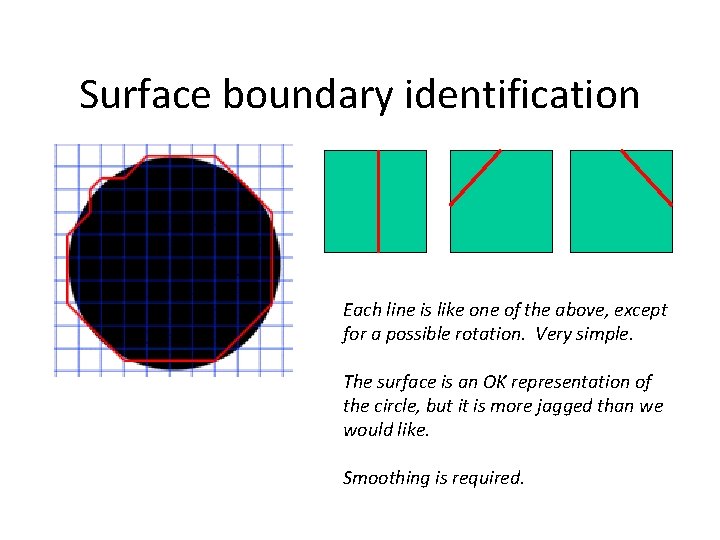
Surface boundary identification Each line is like one of the above, except for a possible rotation. Very simple. The surface is an OK representation of the circle, but it is more jagged than we would like. Smoothing is required.

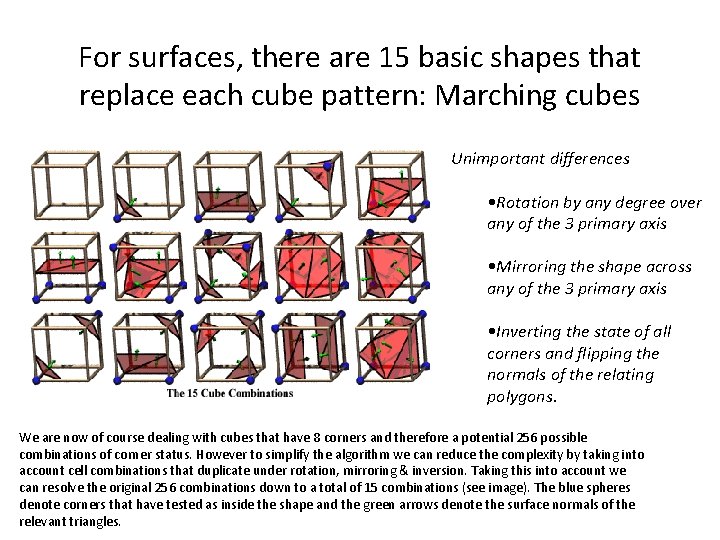
For surfaces, there are 15 basic shapes that replace each cube pattern: Marching cubes Unimportant differences • Rotation by any degree over any of the 3 primary axis • Mirroring the shape across any of the 3 primary axis • Inverting the state of all corners and flipping the normals of the relating polygons. We are now of course dealing with cubes that have 8 corners and therefore a potential 256 possible combinations of corner status. However to simplify the algorithm we can reduce the complexity by taking into account cell combinations that duplicate under rotation, mirroring & inversion. Taking this into account we can resolve the original 256 combinations down to a total of 15 combinations (see image). The blue spheres denote corners that have tested as inside the shape and the green arrows denote the surface normals of the relevant triangles.

Visualization techniques How to manual • Iso-voxel • Segment brain into gray and white matter • Determine the surface boundaries (Marching cubes algorithm) • Smooth the resultant cortical surface

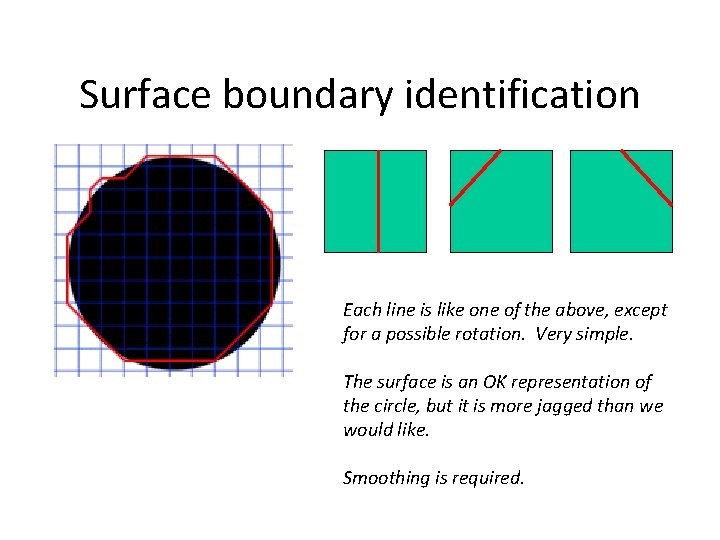
Surface boundary identification Each line is like one of the above, except for a possible rotation. Very simple. The surface is an OK representation of the circle, but it is more jagged than we would like. Smoothing is required.

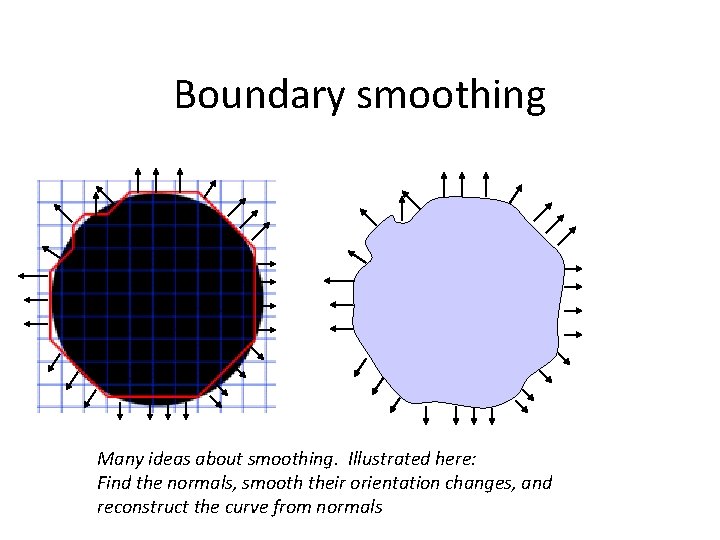
Boundary smoothing Many ideas about smoothing. Illustrated here: Find the normals, smooth their orientation changes, and reconstruct the curve from normals

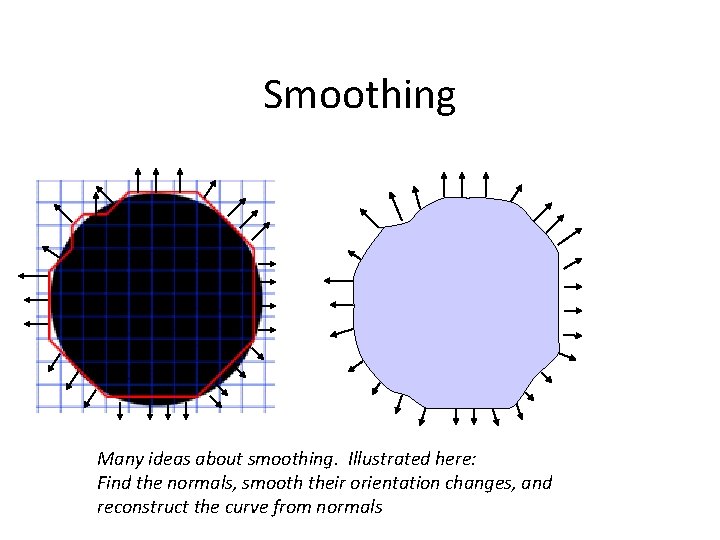
Smoothing Many ideas about smoothing. Illustrated here: Find the normals, smooth their orientation changes, and reconstruct the curve from normals

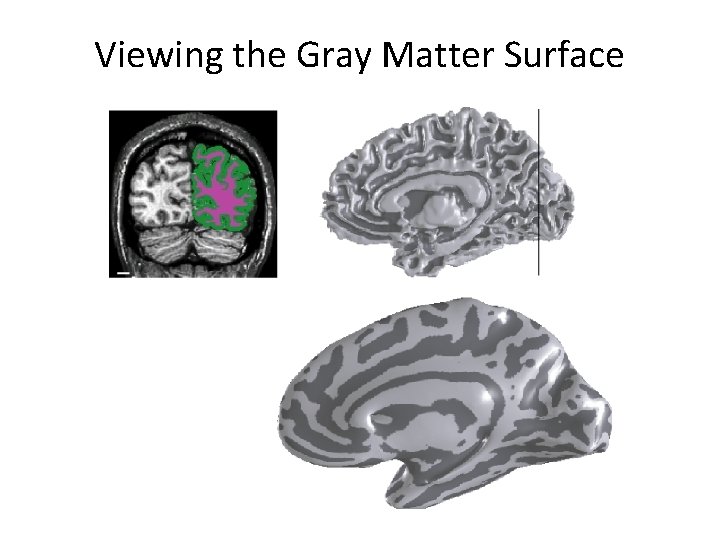
Viewing the Gray Matter Surface

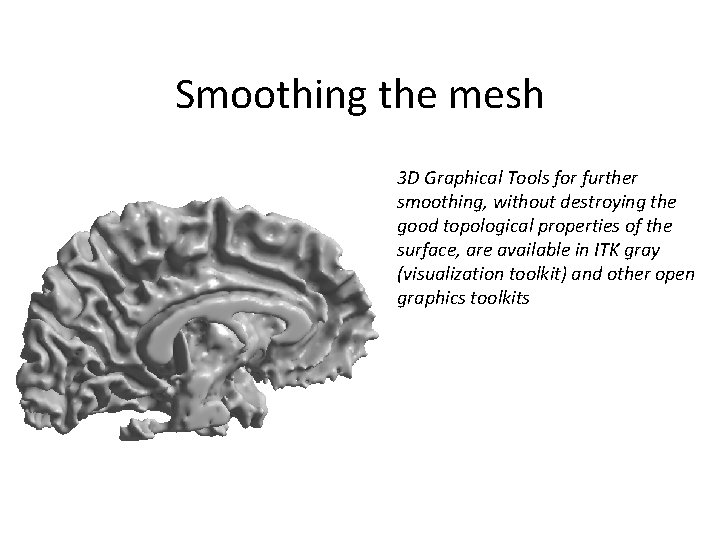
Smoothing the mesh 3 D Graphical Tools for further smoothing, without destroying the good topological properties of the surface, are available in ITK gray (visualization toolkit) and other open graphics toolkits

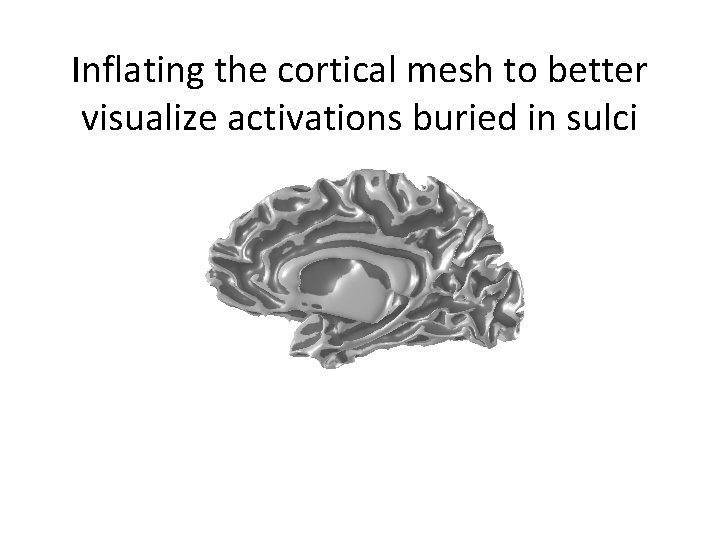
Inflating the cortical mesh to better visualize activations buried in sulci

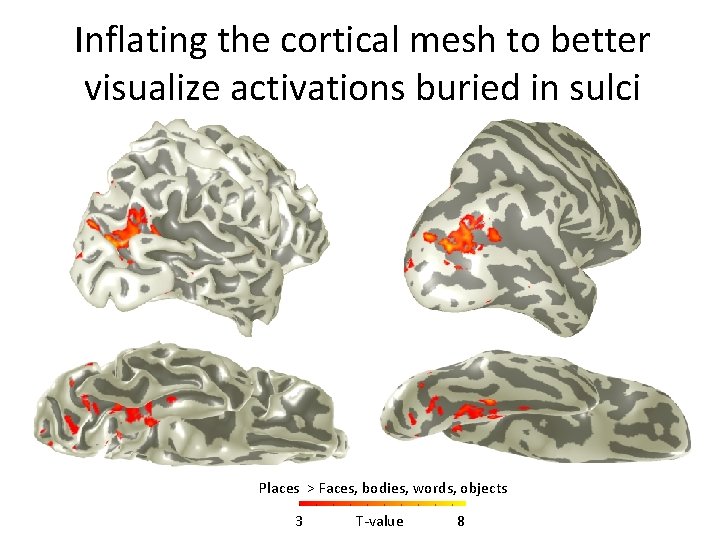
Inflating the cortical mesh to better visualize activations buried in sulci Places > Faces, bodies, words, objects 3 T-value 8

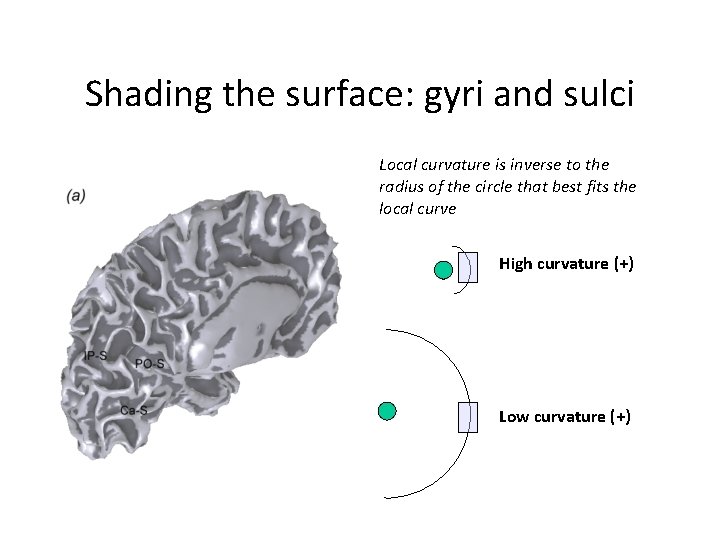
Shading the surface: gyri and sulci Local curvature is inverse to the radius of the circle that best fits the local curve High curvature (+) Low curvature (+)

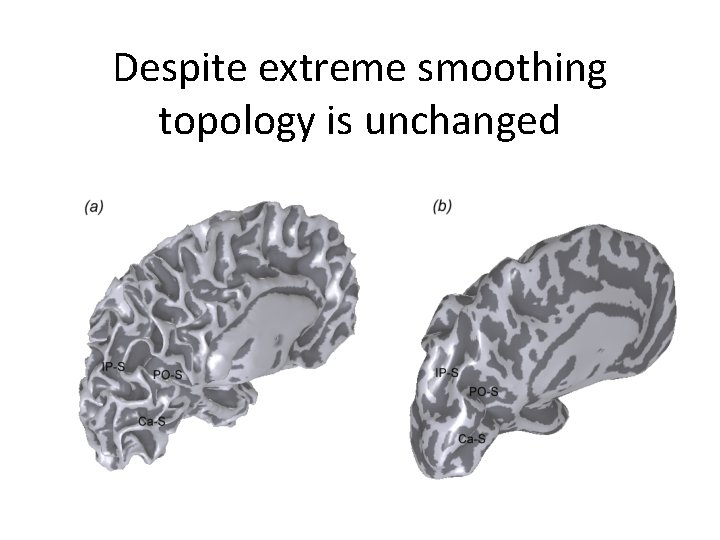
Despite extreme smoothing topology is unchanged