The Importance of Data Transformation in Machine Learning

The Importance of Data Transformation in Machine Learning: Application to PCA Unsupervised Classification of Turbidite Channels, New Zealand PNN Supervised Classification of Salt, Gulf of Mexico Thang Ha, David Lubo, Ichie Yasutaka, Bradley Wallet, and Kurt Marfurt AASPI Consortium Meeting, 2019

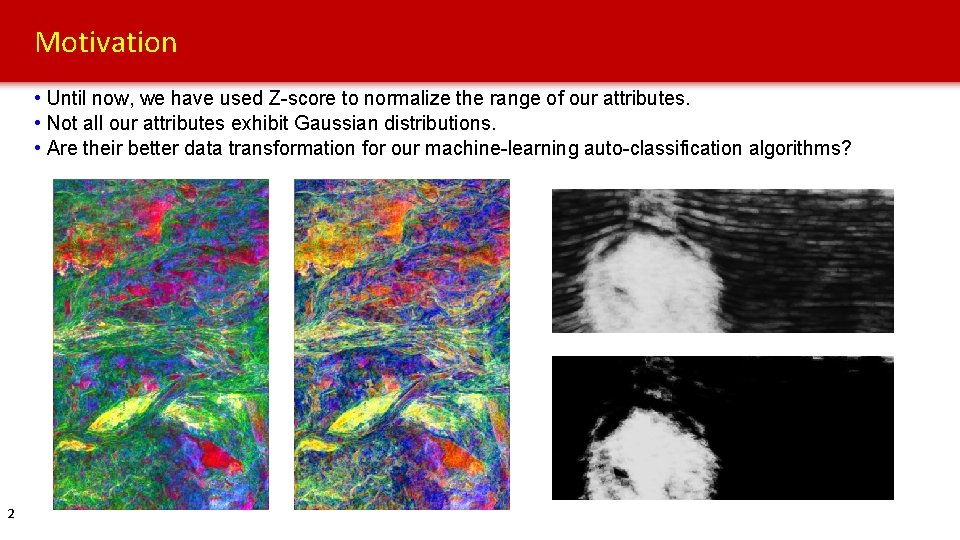
Motivation • Until now, we have used Z-score to normalize the range of our attributes. • Not all our attributes exhibit Gaussian distributions. • Are their better data transformation for our machine-learning auto-classification algorithms? 2

Outline • Motivation • Case Study 1: Unsupervised PCA analysis of a Turbidite Channel System o Geologic Background o Z-score vs Log-normal o PCA Sensitivity to Data Shifting and Scaling • Case Study 2: PNN Supervised Classification of Salt o Facies-by-facies vs all-at-once Data Transformation • Future Work • Conclusions 3

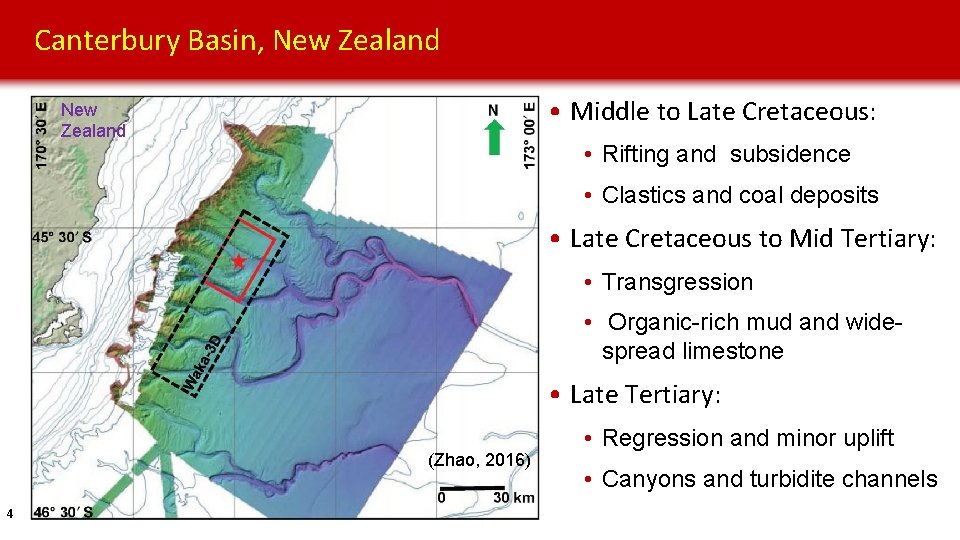
Canterbury Basin, New Zealand • Middle to Late Cretaceous: New Zealand • Rifting and subsidence • Clastics and coal deposits • Late Cretaceous to Mid Tertiary: • Transgression • Organic-rich mud and widespread limestone • Late Tertiary: (Zhao, 2016) 4 • Regression and minor uplift • Canyons and turbidite channels

Input Attributes for Principal Component Analysis (PCA) Curvedness Coherent Energy Low 5 High Low GLCM Entropy High Low High 0 8000 ft

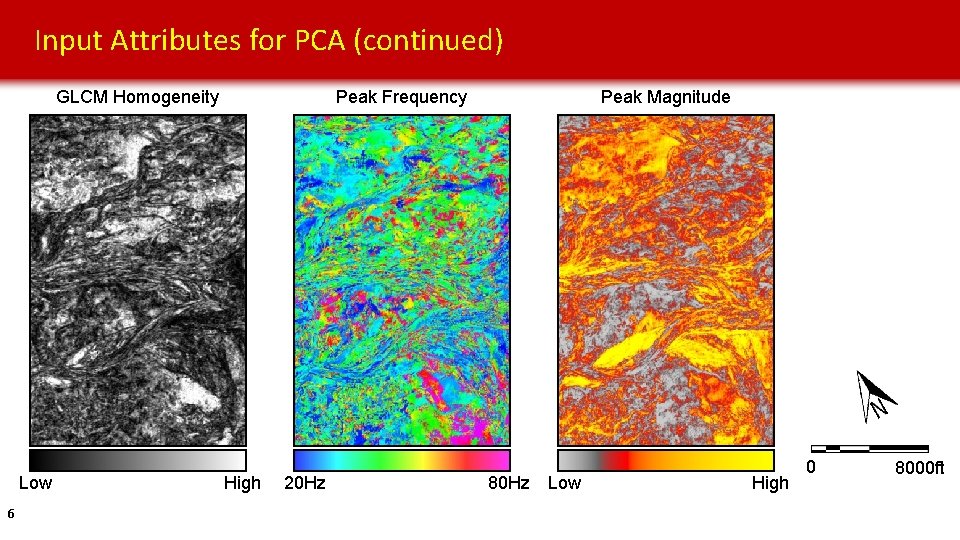
Input Attributes for PCA (continued) Peak Frequency GLCM Homogeneity Low 6 High 20 Hz Peak Magnitude 80 Hz Low High 0 8000 ft

Outline • Motivation • Case Study 1: Unsupervised PCA analysis of a Turbidite Channel System o Geologic Background o Z-score vs Log-normal o PCA Sensitivity to Data Shifting and Scaling • Case Study 2: PNN Supervised Classification of Salt o Facies-by-facies vs all-at-once Data Transformation • Future Work • Conclusions 7

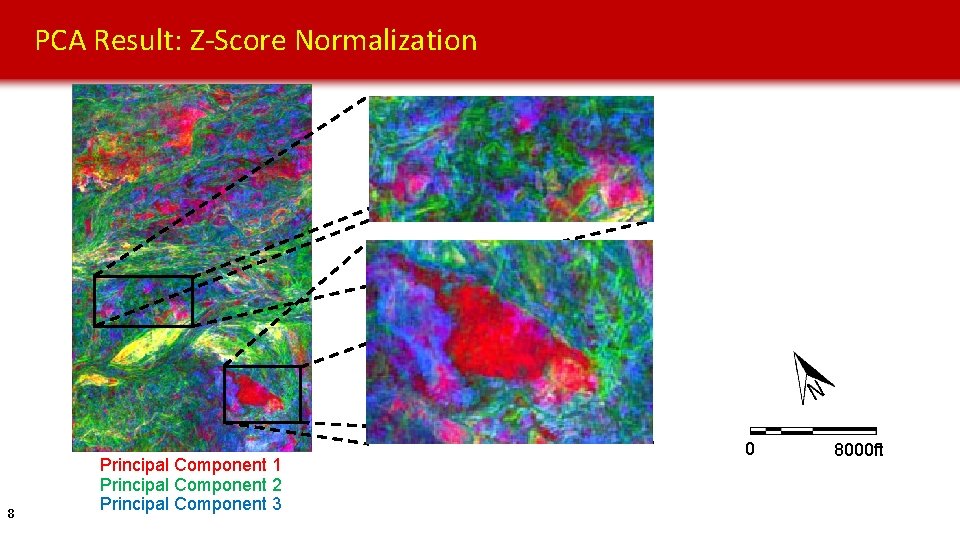
PCA Result: Z-Score Normalization 8 Principal Component 1 Principal Component 2 Principal Component 3 0 8000 ft

PCA Result: Logarithmic Normalization 9 Principal Component 1 Principal Component 2 Principal Component 3 0 8000 ft

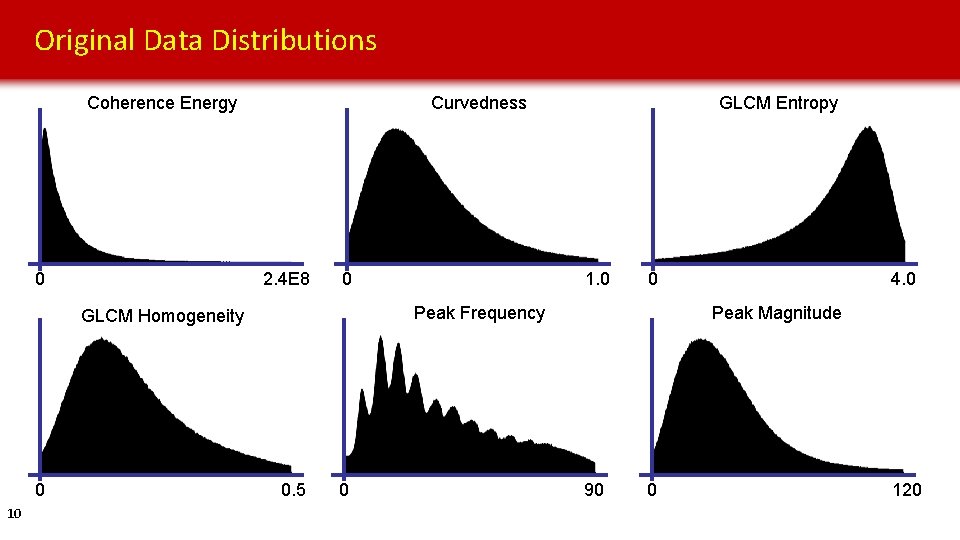
Original Data Distributions Coherence Energy 0 Curvedness 2. 4 E 8 0 10 1. 0 0 Peak Frequency GLCM Homogeneity 0 GLCM Entropy 0. 5 0 4. 0 Peak Magnitude 90 0 120

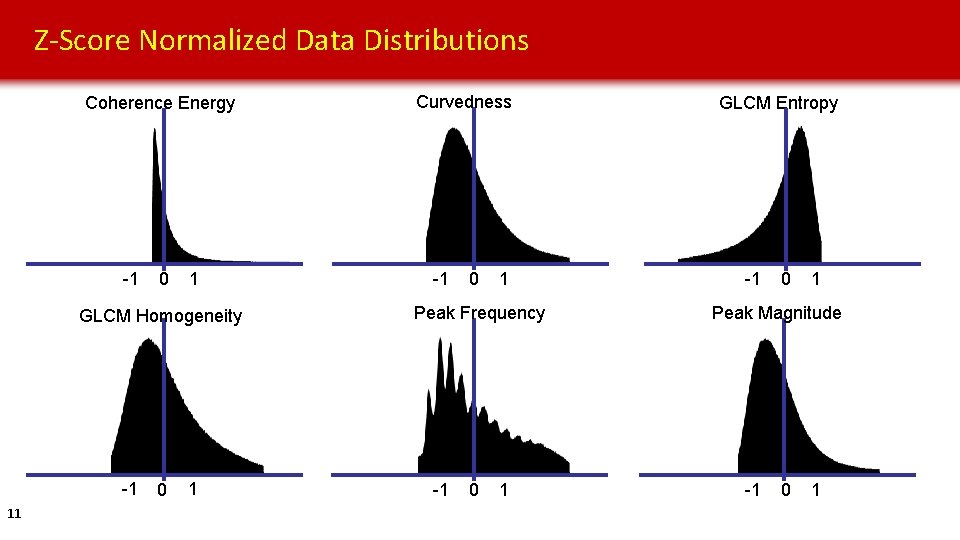
Z-Score Normalized Data Distributions Coherence Energy -1 0 1 GLCM Homogeneity -1 11 0 1 Curvedness -1 0 1 Peak Frequency -1 0 1 GLCM Entropy -1 0 1 Peak Magnitude -1 0 1

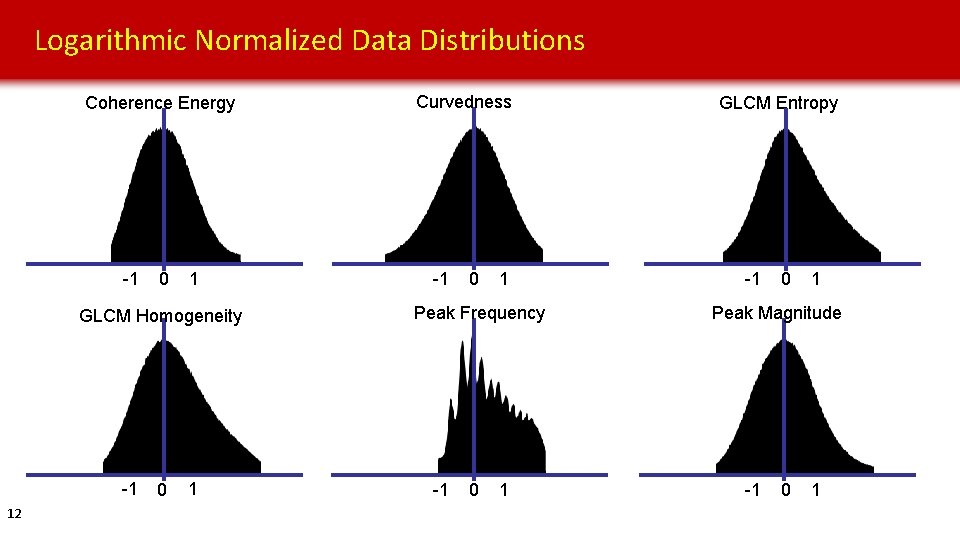
Logarithmic Normalized Data Distributions Coherence Energy -1 0 1 GLCM Homogeneity -1 12 0 1 Curvedness -1 0 1 Peak Frequency -1 0 1 GLCM Entropy -1 0 1 Peak Magnitude -1 0 1

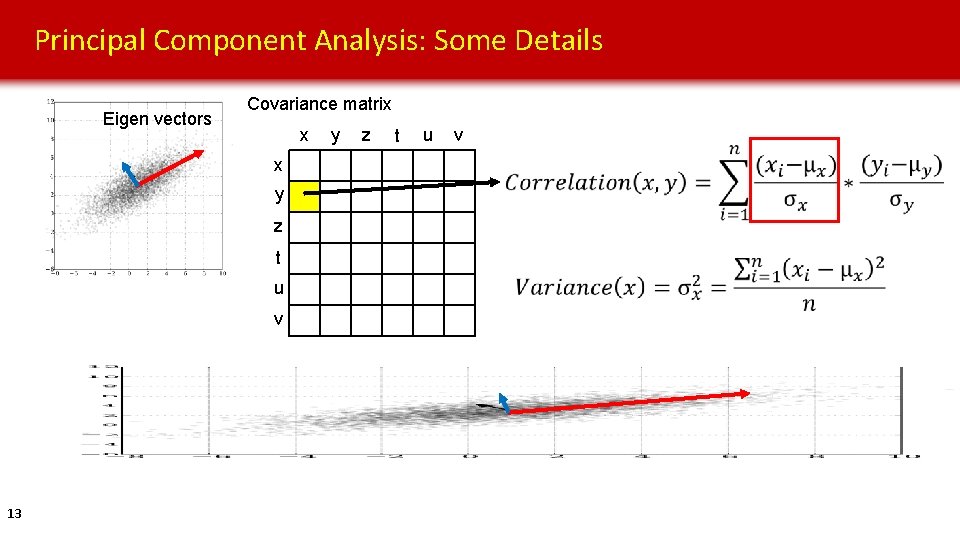
Principal Component Analysis: Some Details Eigen vectors Covariance matrix x x y z t u v 13 y z t u v

Data Transformation: Generalize Z-Score Normalization 14 AASPI Logarithmic Normalization

Logarithmic Normalization: Expectation vs Reality Your Face 15

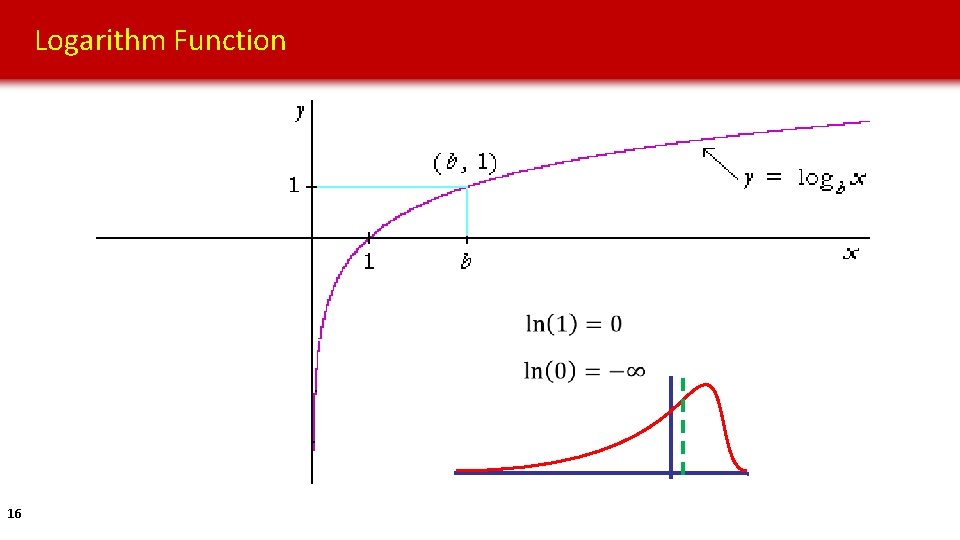
Logarithm Function 16

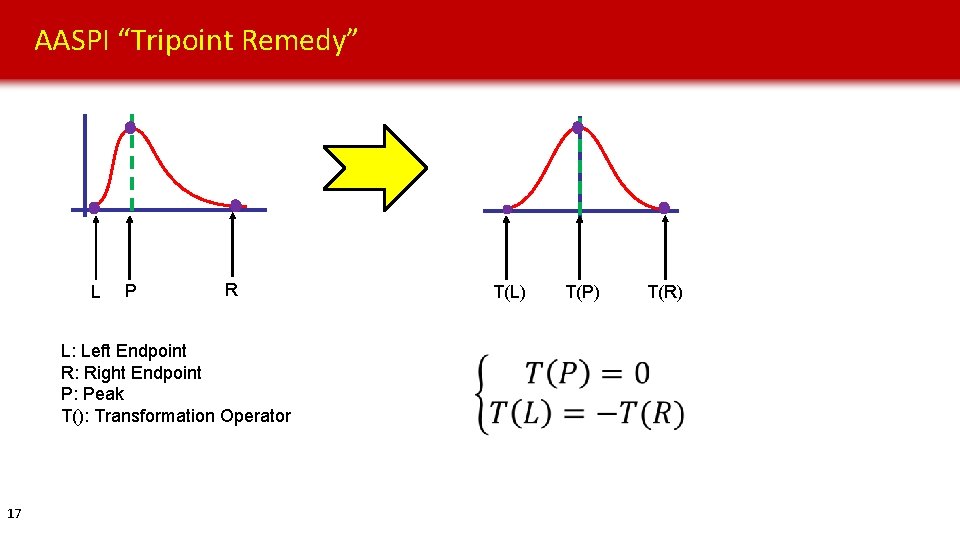
AASPI “Tripoint Remedy” L P R L: Left Endpoint R: Right Endpoint P: Peak T(): Transformation Operator 17 T(L) T(P) T(R)

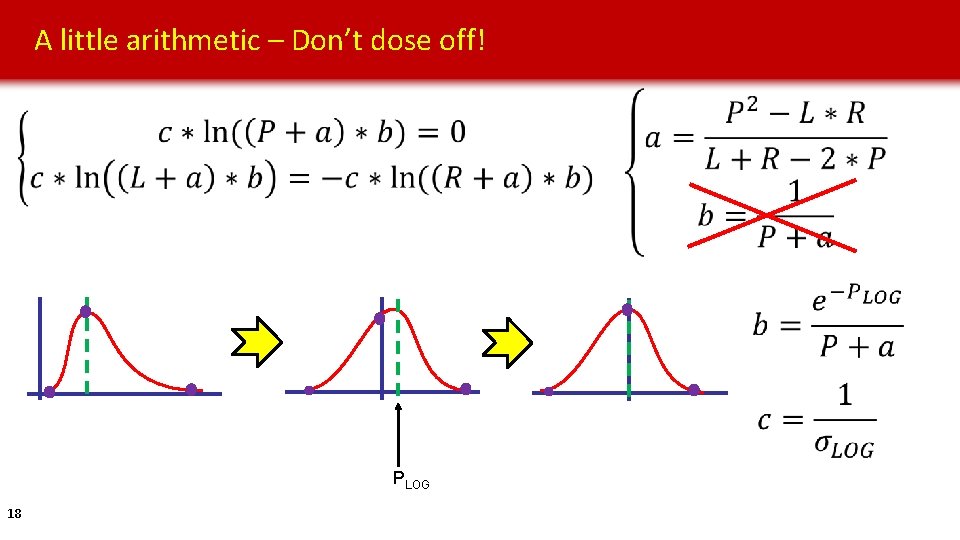
A little arithmetic – Don’t dose off! PLOG 18

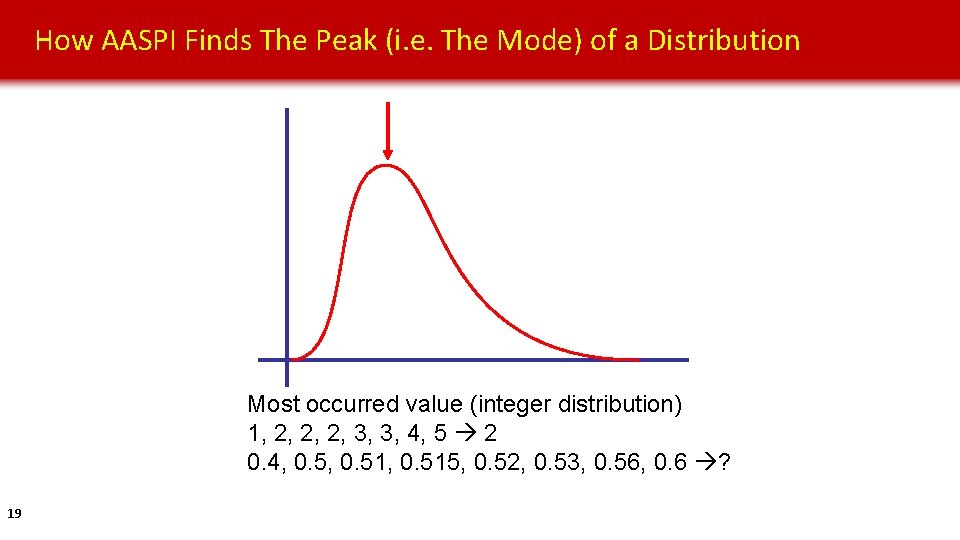
How AASPI Finds The Peak (i. e. The Mode) of a Distribution Most occurred value (integer distribution) 1, 2, 2, 2, 3, 3, 4, 5 2 0. 4, 0. 51, 0. 515, 0. 52, 0. 53, 0. 56, 0. 6 ? 19

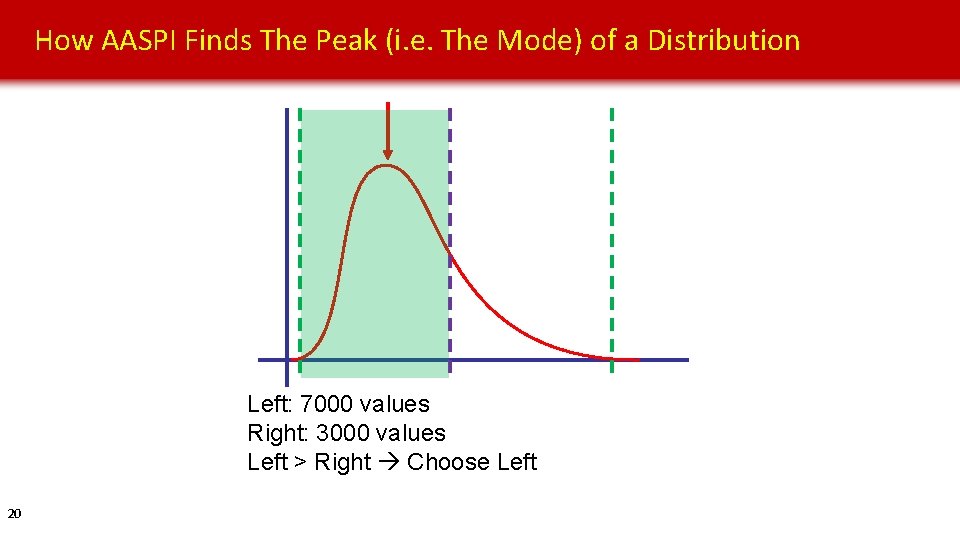
How AASPI Finds The Peak (i. e. The Mode) of a Distribution Left: 7000 values Right: 3000 values Left > Right Choose Left 20

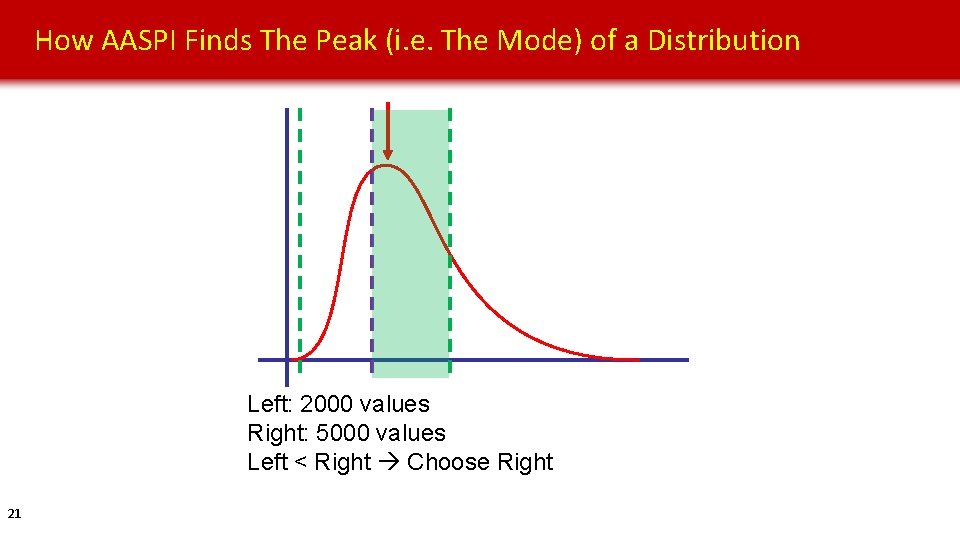
How AASPI Finds The Peak (i. e. The Mode) of a Distribution Left: 2000 values Right: 5000 values Left < Right Choose Right 21

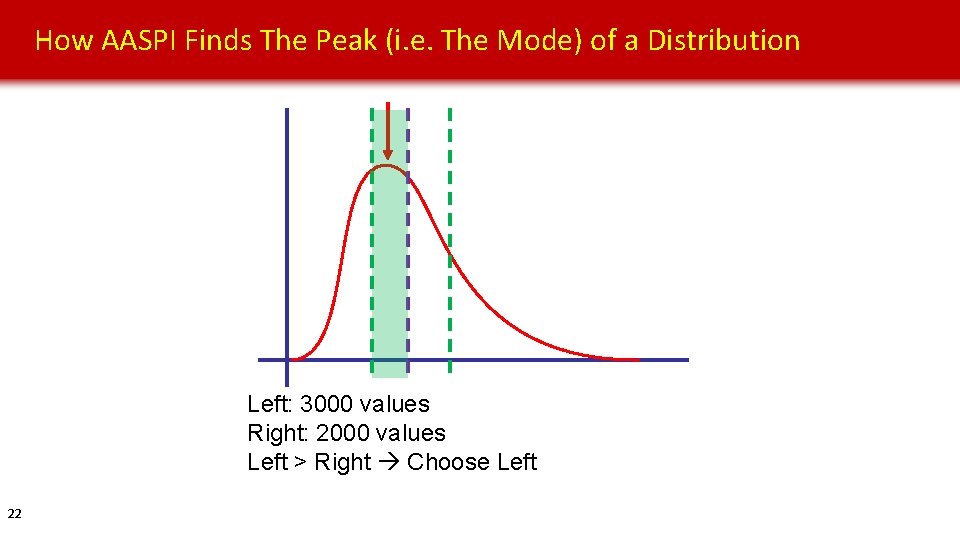
How AASPI Finds The Peak (i. e. The Mode) of a Distribution Left: 3000 values Right: 2000 values Left > Right Choose Left 22

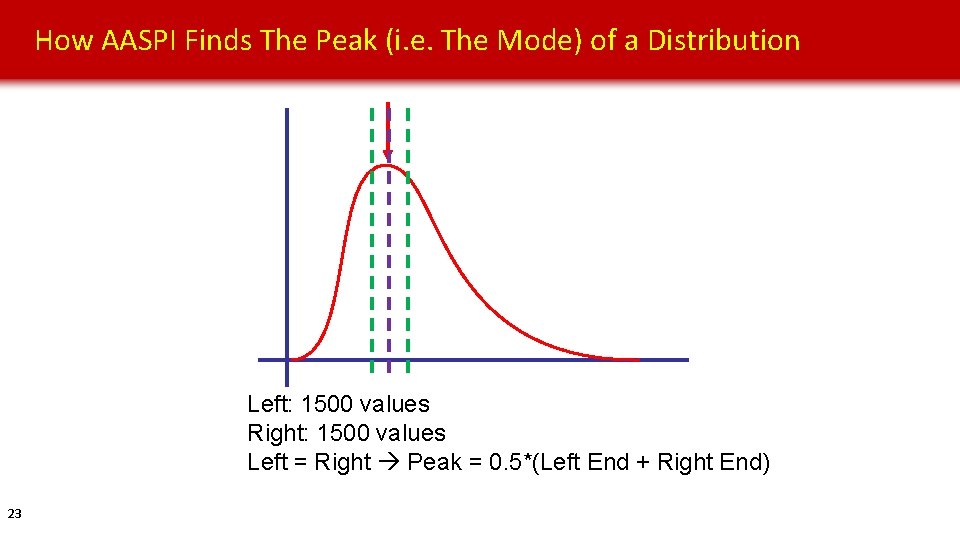
How AASPI Finds The Peak (i. e. The Mode) of a Distribution Left: 1500 values Right: 1500 values Left = Right Peak = 0. 5*(Left End + Right End) 23

No more MATH, I promise… • Motivation • Case Study 1: Unsupervised PCA analysis of a Turbidite Channel System o Geologic Background o Z-score vs Log-normal o PCA Sensitivity to Data Shifting and Scaling • Case Study 2: PNN Supervised Classification of Salt o Facies-by-facies vs all-at-once Data Transformation • Future Work • Conclusions 24

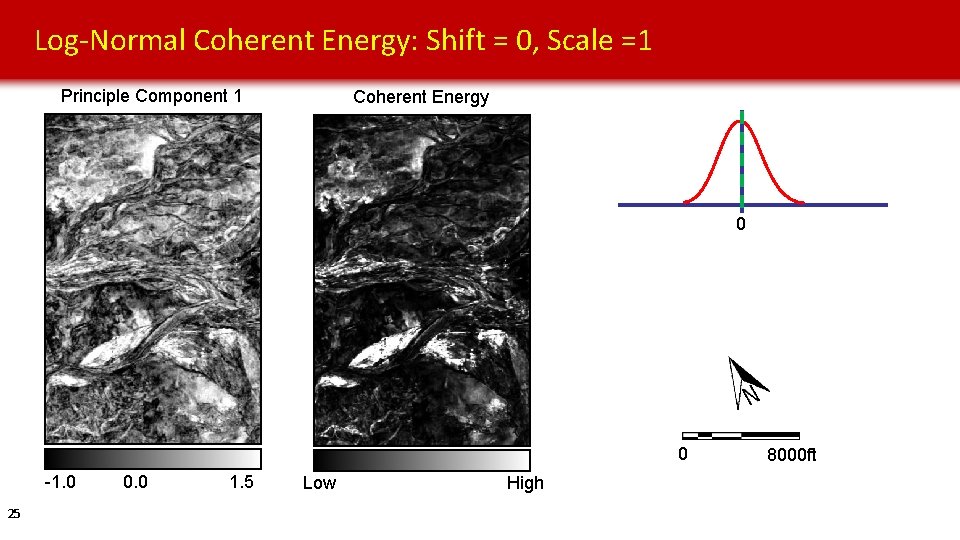
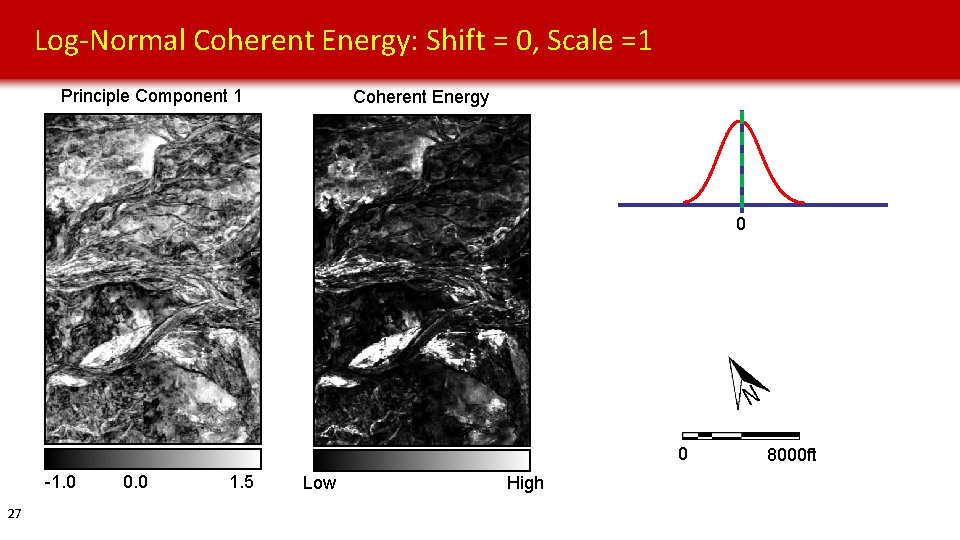
Log-Normal Coherent Energy: Shift = 0, Scale =1 Principle Component 1 Coherent Energy 0 0 -1. 0 25 0. 0 1. 5 Low High 8000 ft

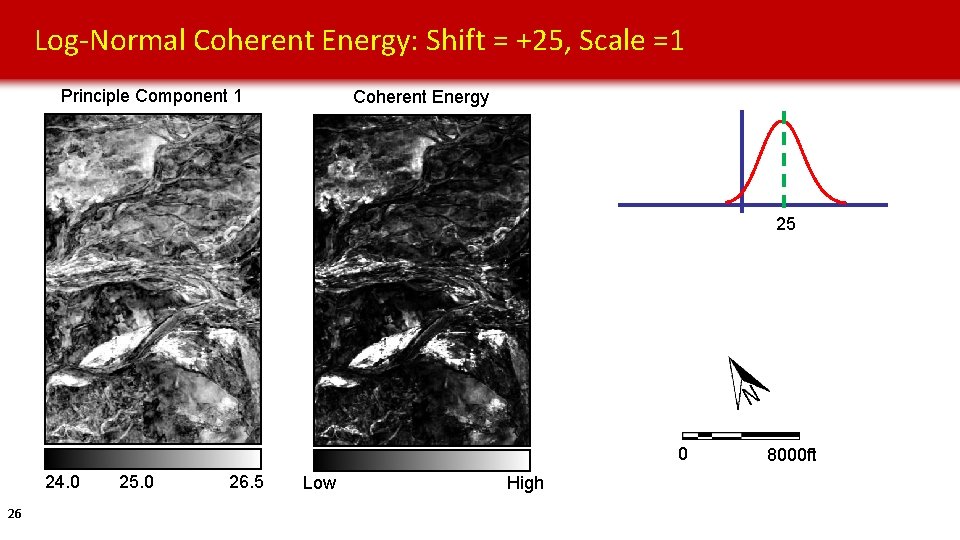
Log-Normal Coherent Energy: Shift = +25, Scale =1 Principle Component 1 Coherent Energy 25 0 24. 0 26 25. 0 26. 5 Low High 8000 ft

Log-Normal Coherent Energy: Shift = 0, Scale =1 Principle Component 1 Coherent Energy 0 0 -1. 0 27 0. 0 1. 5 Low High 8000 ft

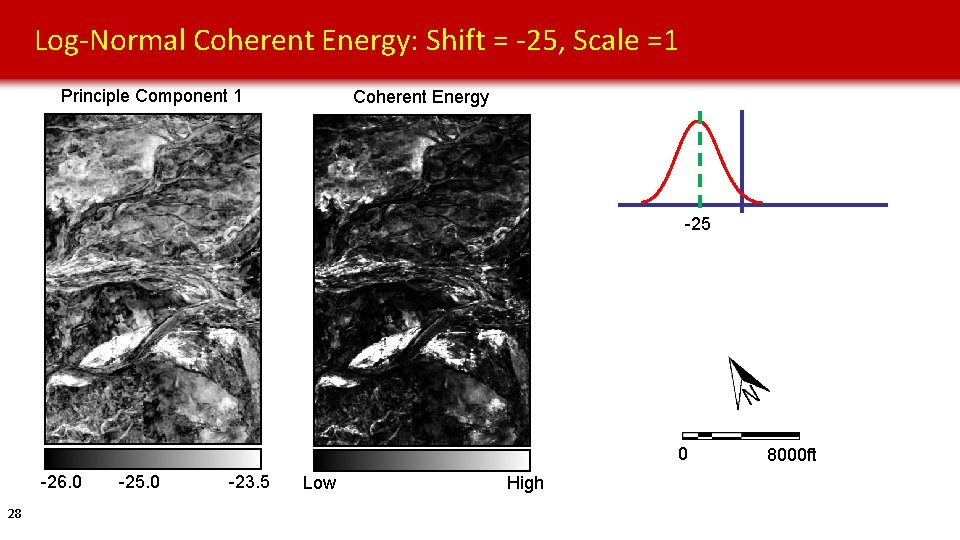
Log-Normal Coherent Energy: Shift = -25, Scale =1 Principle Component 1 Coherent Energy -25 0 -26. 0 28 -25. 0 -23. 5 Low High 8000 ft

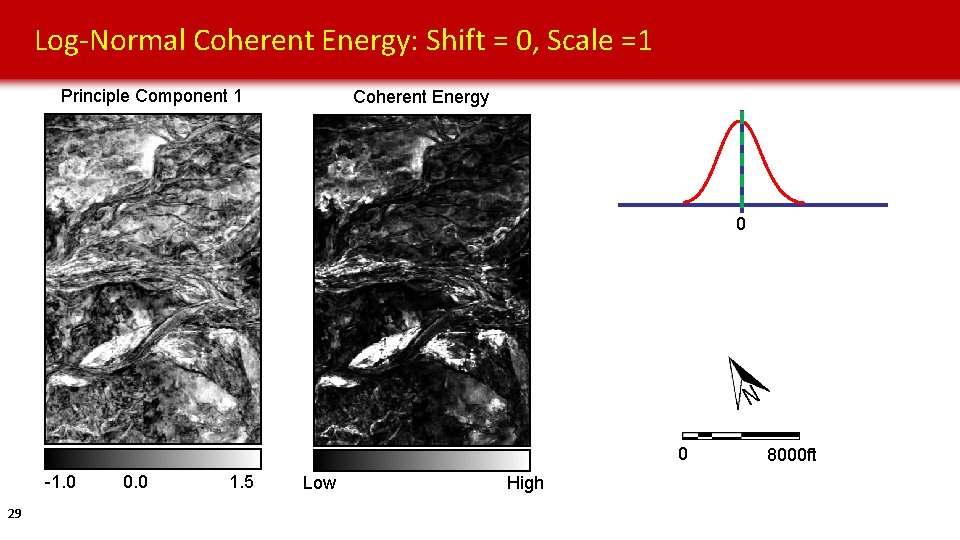
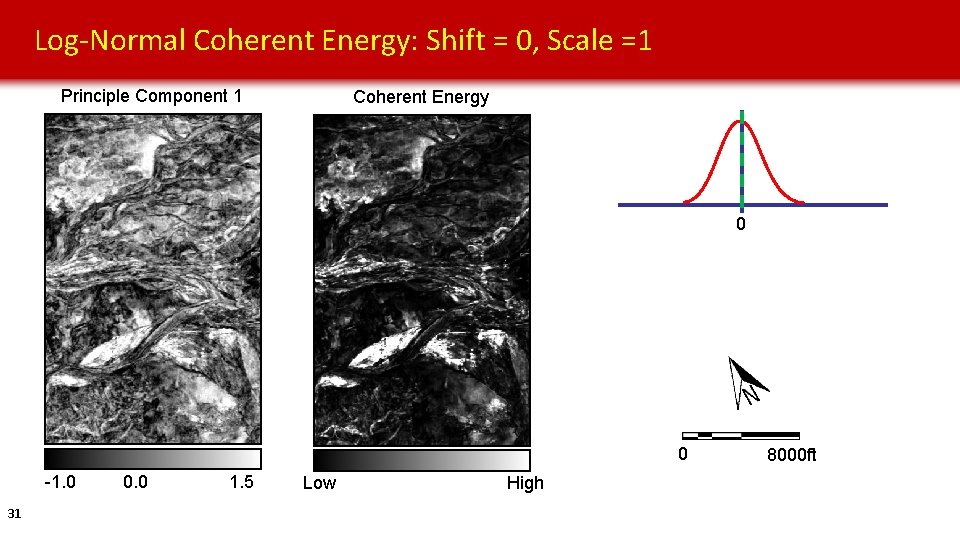
Log-Normal Coherent Energy: Shift = 0, Scale =1 Principle Component 1 Coherent Energy 0 0 -1. 0 29 0. 0 1. 5 Low High 8000 ft

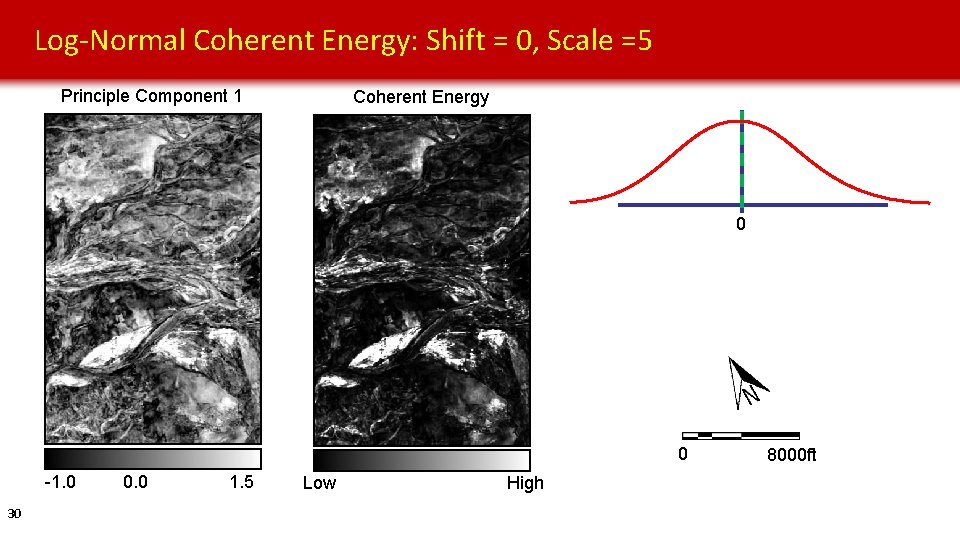
Log-Normal Coherent Energy: Shift = 0, Scale =5 Principle Component 1 Coherent Energy 0 0 -1. 0 30 0. 0 1. 5 Low High 8000 ft

Log-Normal Coherent Energy: Shift = 0, Scale =1 Principle Component 1 Coherent Energy 0 0 -1. 0 31 0. 0 1. 5 Low High 8000 ft

Log-Normal Coherent Energy: Shift = 0, Scale =0. 2 Principle Component 1 Coherent Energy 0 0 -1. 0 32 0. 0 1. 5 Low High 8000 ft

Outline • Motivation • Case Study 1: Unsupervised PCA analysis of a Turbidite Channel System o Geologic Background o Z-score vs Log-normal o PCA Sensitivity to Data Shifting and Scaling • Case Study 2: PNN Supervised Classification of Salt (Eugene Island, GOM) o Facies-by-facies vs all-at-once Data Transformation • Future Work • Conclusions 33

Gulf of Mexico: Corendered seismic amplitude and coherece Time (s) Amplitude Positive 0 1. 0 Negative 1. 5 Coherence High 2. 0 Low 2. 5 34 0 10000 ft

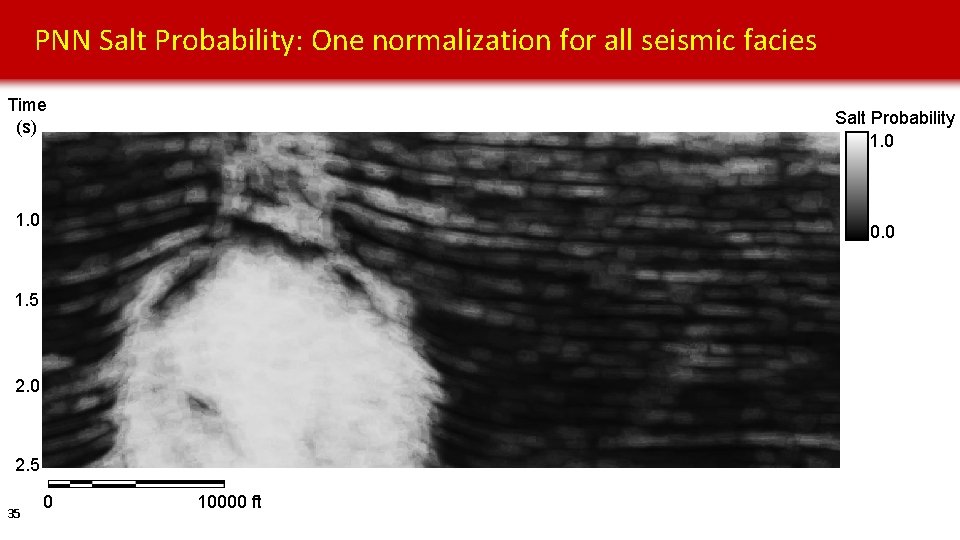
PNN Salt Probability: One normalization for all seismic facies Time (s) Salt Probability 1. 0 0. 0 1. 5 2. 0 2. 5 35 0 10000 ft

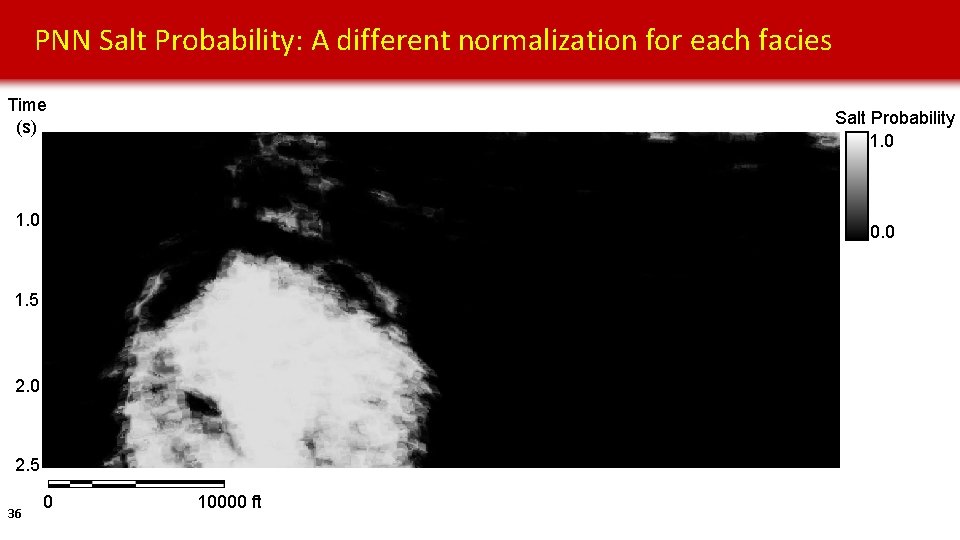
PNN Salt Probability: A different normalization for each facies Time (s) Salt Probability 1. 0 0. 0 1. 5 2. 0 2. 5 36 0 10000 ft

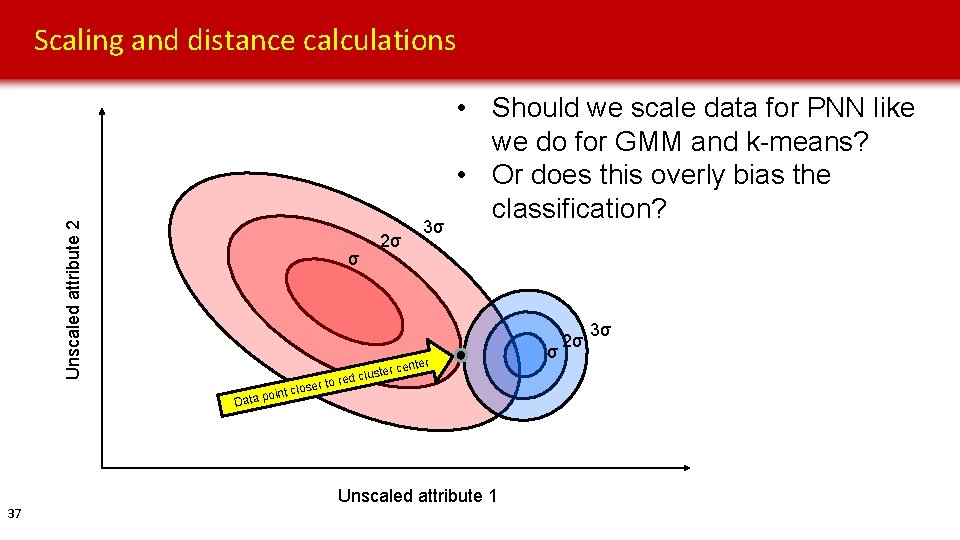
Unscaled attribute 2 Scaling and distance calculations σ oint cl Data p 37 2σ 3σ • Should we scale data for PNN like we do for GMM and k-means? • Or does this overly bias the classification? er r cent e t s u l ed c er to r os Unscaled attribute 1 σ 2σ 3σ

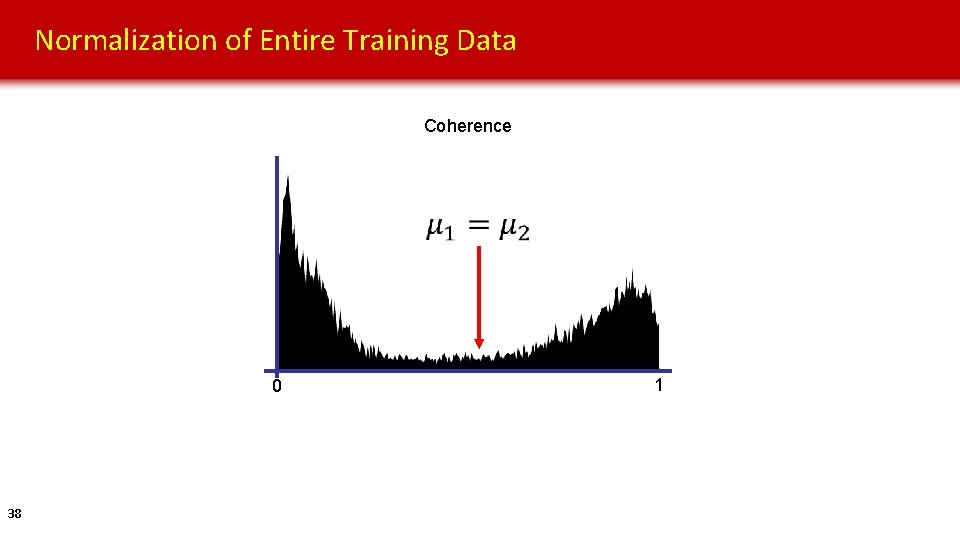
Normalization of Entire Training Data Coherence 0 38 1

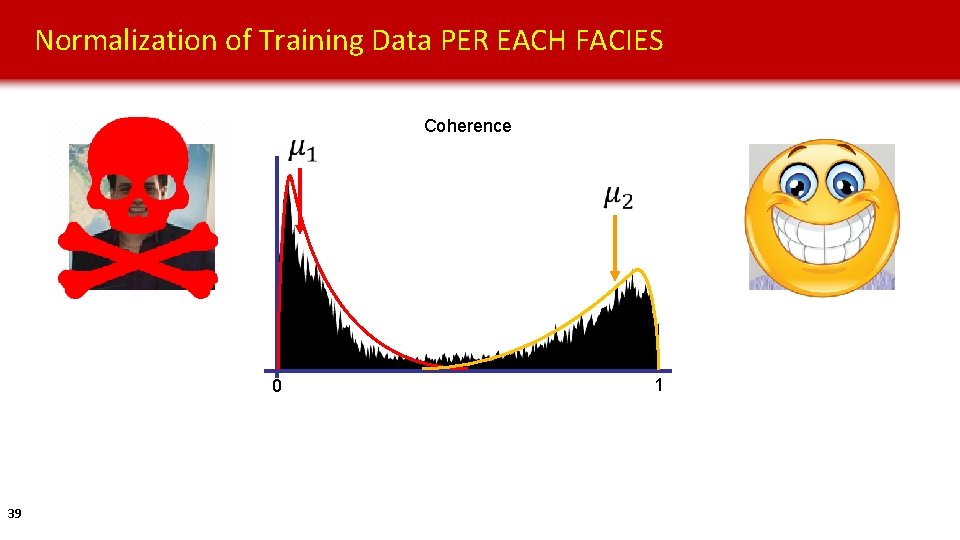
Normalization of Training Data PER EACH FACIES Coherence 0 39 1

Future Work • Test different data transformations on other machine-learning algorithms, such as SOM, GTM, GMM, PSVM, RFC, etc. 40

Conclusions • Data transformation significantly changes the results of PCA unsupervised classification. • The results of PCA have better color contrast, higher level of details, and are potentially capable of differentiating more seismic facies when transformed data distributions approach Gaussian distributions. • Logarithmic normalization, when computed correctly, can approximate an allpositive data distribution by a Gaussian distribution. • Per-facies transformation makes PNN supervised classification more robust than all-at-once transformation, but could be too biased (and possibly overfitting? ) 41

Any questions?