The Impact of Communication Locality on LargeScale Multiprocessor

The Impact of Communication Locality on Large-Scale Multiprocessor Performance Author: Kirk Johnson Mel Tsai CS 258 5/8/2002 1

Introduction • Analytical study of Non-Uniform Communication Latency (NUCL) architectures • Attempts to: ® Show that only linear speedups are possible as average communication latency decreases ® Show that speedups due to exploiting physical locality aren’t great as machine sizes scale 2

The Analytical Model • Study draws conclusions from mathematical formulations of the system components: 1. The application 2. Transactions initiated by the application 3. The network 3

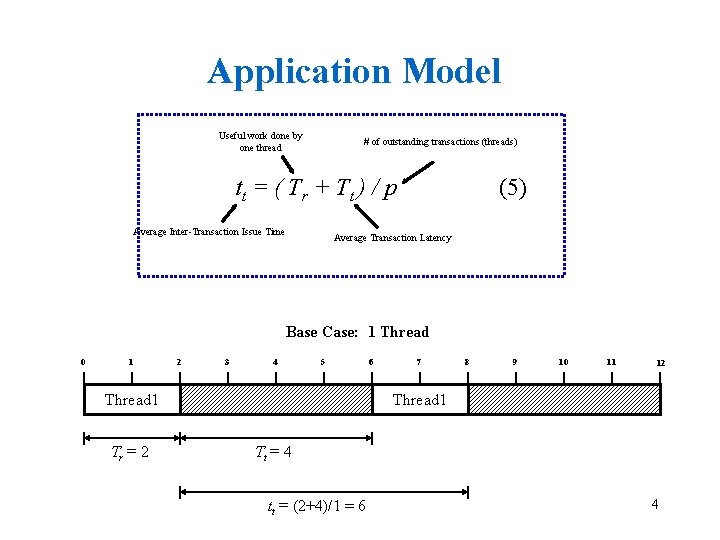
Application Model Useful work done by one thread # of outstanding transactions (threads) t t = ( Tr + Tt ) / p Average Inter-Transaction Issue Time (5) Average Transaction Latency Base Case: 1 Thread 0 1 2 3 4 5 Thread 1 Tr = 2 6 7 8 9 10 11 12 Thread 1 Tt = 4 tt = (2+4)/1 = 6 4

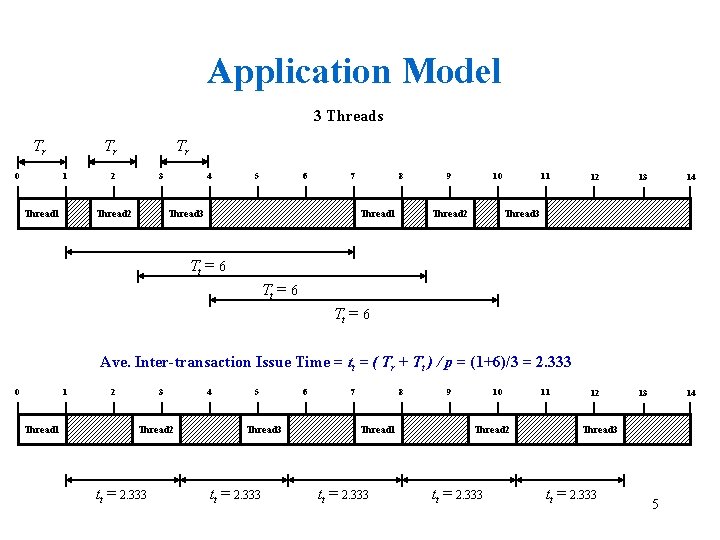
Application Model 3 Threads Tr Tr 0 1 Thread 1 Tr 2 3 Thread 2 4 5 6 7 Thread 3 8 Thread 1 9 10 Thread 2 11 12 13 14 Thread 3 Tt = 6 Ave. Inter-transaction Issue Time = tt = ( Tr + Tt ) / p = (1+6)/3 = 2. 333 0 1 Thread 1 2 3 Thread 2 tt = 2. 333 4 5 Thread 3 tt = 2. 333 6 7 8 Thread 1 tt = 2. 333 9 10 Thread 2 tt = 2. 333 11 Thread 3 tt = 2. 333 5

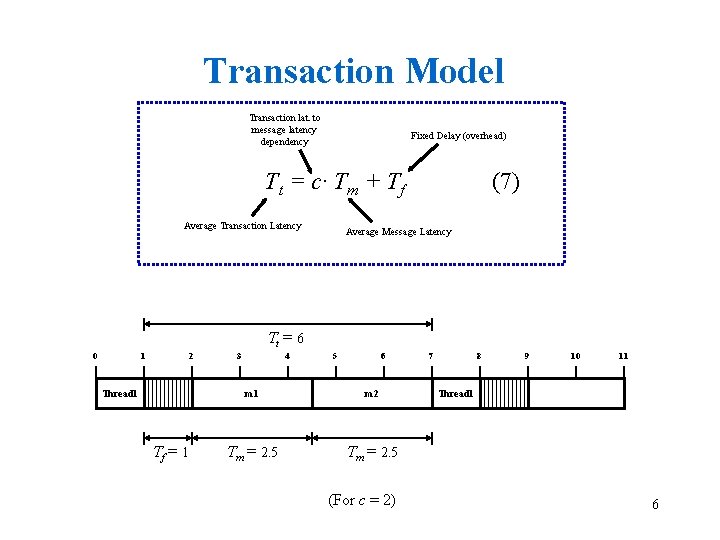
Transaction Model Transaction lat. to message latency dependency Fixed Delay (overhead) Tt = c· Tm + Tf Average Transaction Latency (7) Average Message Latency Tt = 6 0 1 2 Thread 1 Tf = 1 3 4 5 6 m 1 m 2 Tm = 2. 5 (For c = 2) 7 8 9 10 11 Thread 1 6

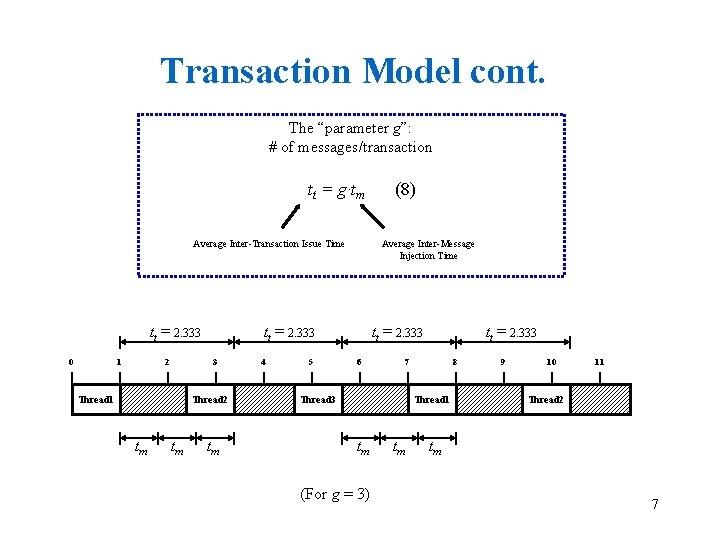
Transaction Model cont. The “parameter g”: # of messages/transaction tt = g·tm Average Inter-Transaction Issue Time tt = 2. 333 0 1 2 Thread 1 Thread 2 tm tm Average Inter-Message Injection Time tt = 2. 333 3 tm 4 5 (8) tt = 2. 333 6 tt = 2. 333 7 Thread 3 8 Thread 1 tm (For g = 3) tm 9 10 11 Thread 2 tm 7

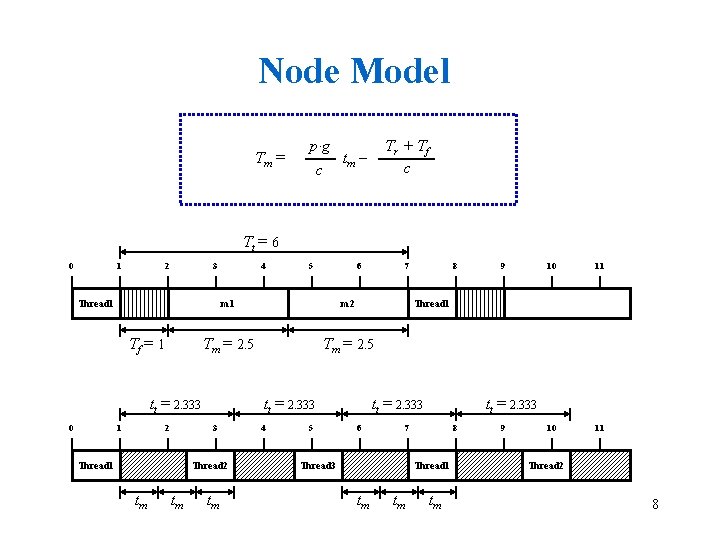
Node Model Tm = p·g c Tr + Tf c tm – Tt = 6 0 1 2 3 Thread 1 Tf = 1 4 1 2 Tm = 2. 5 tm tm 4 5 8 9 10 11 Thread 1 tt = 2. 333 Thread 2 tm 7 m 2 3 Thread 1 6 m 1 tt = 2. 333 0 5 tt = 2. 333 6 tt = 2. 333 7 Thread 3 8 Thread 1 tm tm tm 9 Thread 2 8

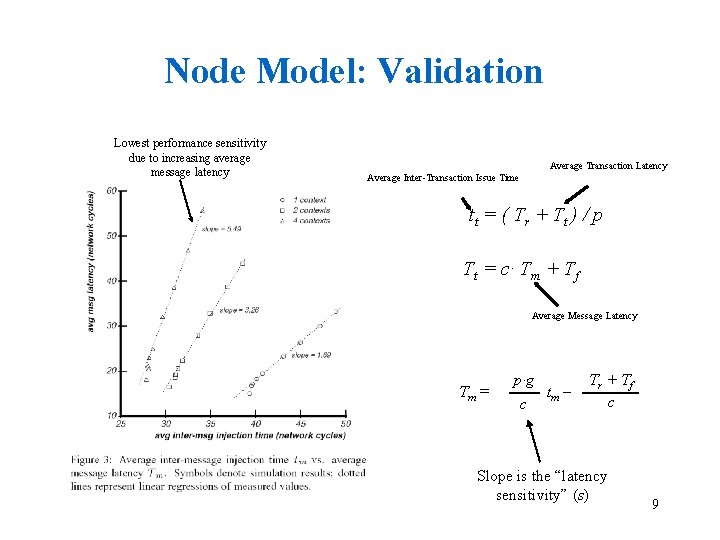
Node Model: Validation Lowest performance sensitivity due to increasing average message latency Average Transaction Latency Average Inter-Transaction Issue Time t t = ( Tr + Tt ) / p Tt = c· Tm + Tf Average Message Latency Tm = p·g c tm – Tr + Tf c Slope is the “latency sensitivity” (s) 9

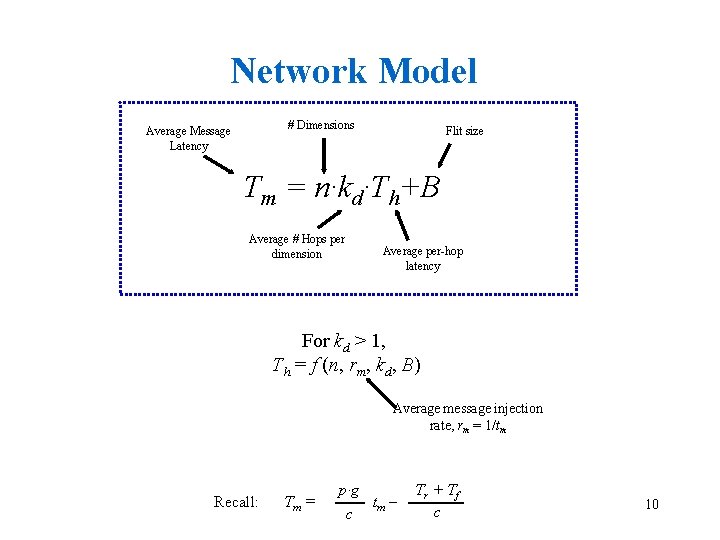
Network Model # Dimensions Average Message Latency Flit size Tm = n·kd·Th+B Average # Hops per dimension Average per-hop latency For kd > 1, Th = f (n, rm, kd, B) Average message injection rate, rm = 1/tm Recall: Tm = p·g c tm – Tr + Tf c 10

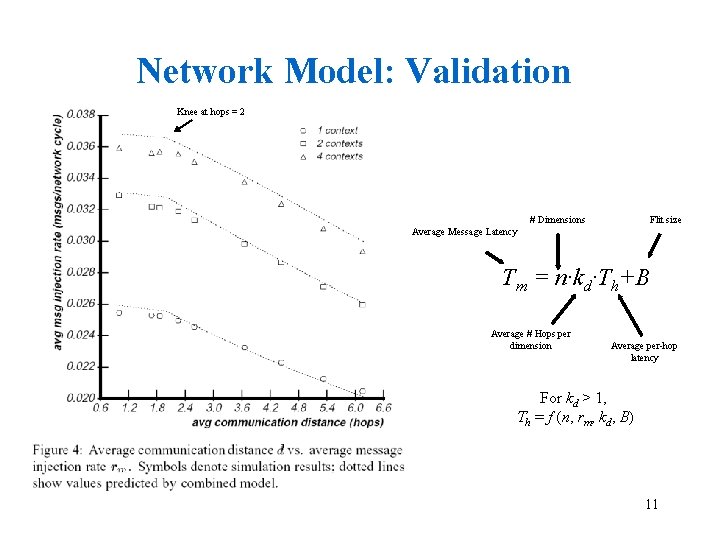
Network Model: Validation Knee at hops = 2 # Dimensions Flit size Average Message Latency Tm = n·kd·Th+B Average # Hops per dimension Average per-hop latency For kd > 1, Th = f (n, rm, kd, B) 11

“L ine ar” Network Model: Validation #2 # Dimensions Flit size Average Message Latency Knee at hops = 2 Tm = n·kd·Th+B Average # Hops per dimension Average per-hop latency For kd > 1, Th = f (n, rm, kd, B) 12

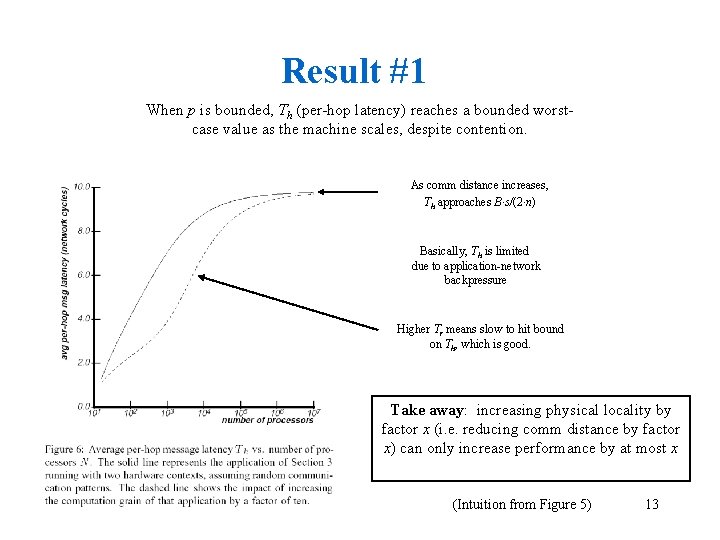
Result #1 When p is bounded, Th (per-hop latency) reaches a bounded worstcase value as the machine scales, despite contention. As comm distance increases, Th approaches B·s/(2·n) Basically, Th is limited due to application-network backpressure Higher Tr means slow to hit bound on Th, which is good. Take away: increasing physical locality by factor x (i. e. reducing comm distance by factor x) can only increase performance by at most x (Intuition from Figure 5) 13

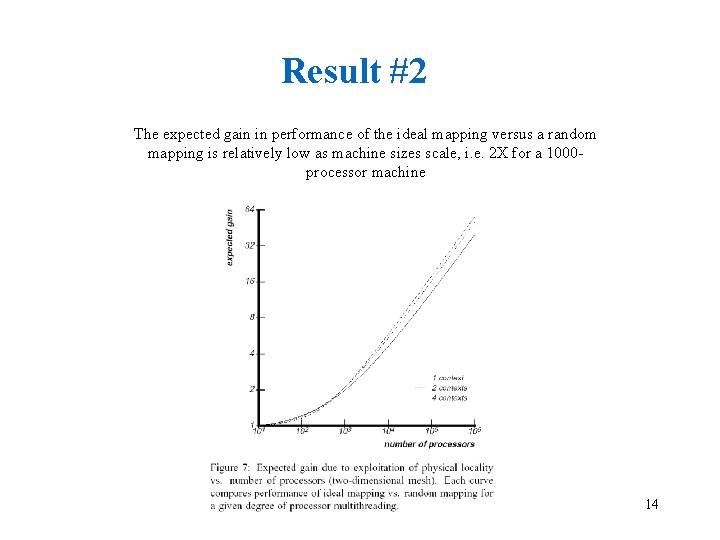
Result #2 The expected gain in performance of the ideal mapping versus a random mapping is relatively low as machine sizes scale, i. e. 2 X for a 1000 processor machine 14

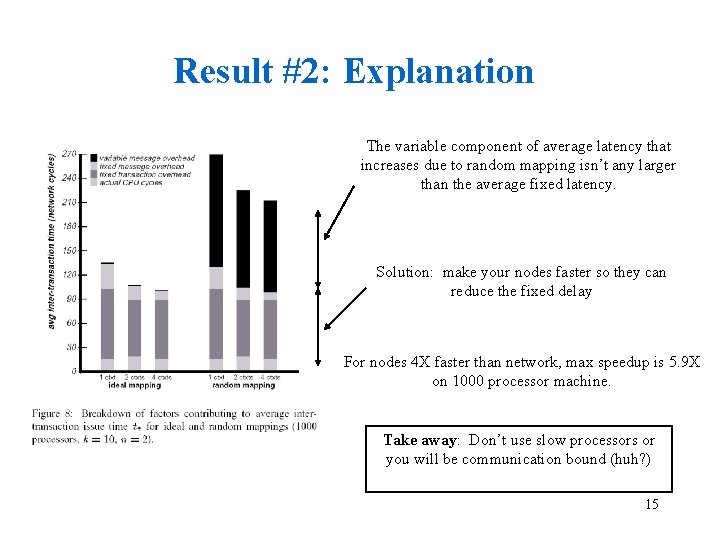
Result #2: Explanation The variable component of average latency that increases due to random mapping isn’t any larger than the average fixed latency. Solution: make your nodes faster so they can reduce the fixed delay For nodes 4 X faster than network, max speedup is 5. 9 X on 1000 processor machine. Take away: Don’t use slow processors or you will be communication bound (huh? ) 15