The Hyperbola A hyperbola is the collection of

The Hyperbola

A hyperbola is the collection of points in the plane the difference of whose distances from two fixed points, called the foci, is a constant.

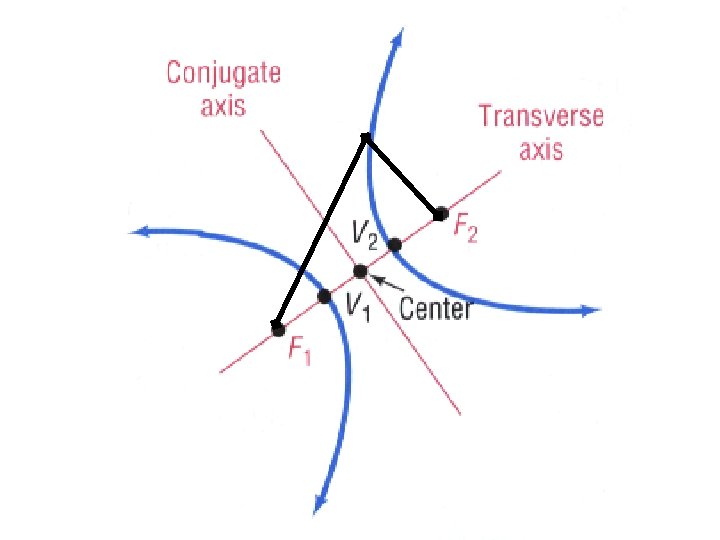
Hyperbola with Transverse Axis Parallel to the x-Axis; Center at (h, k) where b 2 = c 2 - a 2.

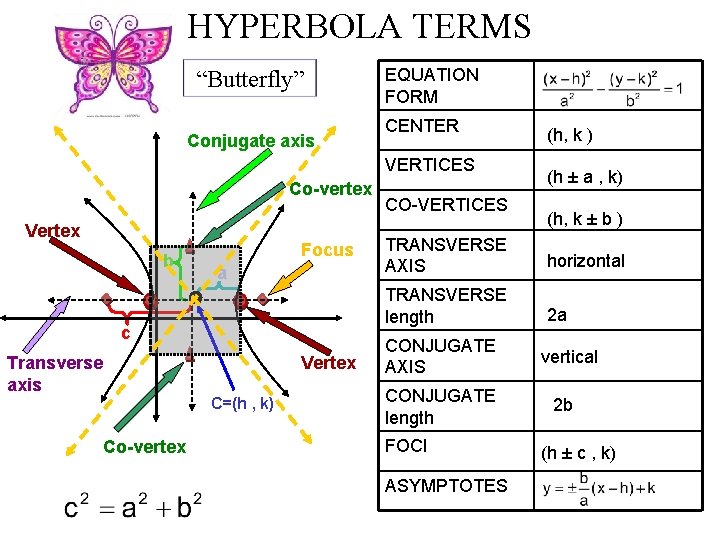
HYPERBOLA TERMS “Butterfly” Conjugate axis EQUATION FORM CENTER VERTICES Co-vertex Vertex b Focus a c Transverse axis Vertex C=(h , k) Co-vertex CO-VERTICES (h, k ) (h ± a , k) (h, k ± b ) TRANSVERSE AXIS horizontal TRANSVERSE length 2 a CONJUGATE AXIS CONJUGATE length FOCI ASYMPTOTES vertical 2 b (h ± c , k)

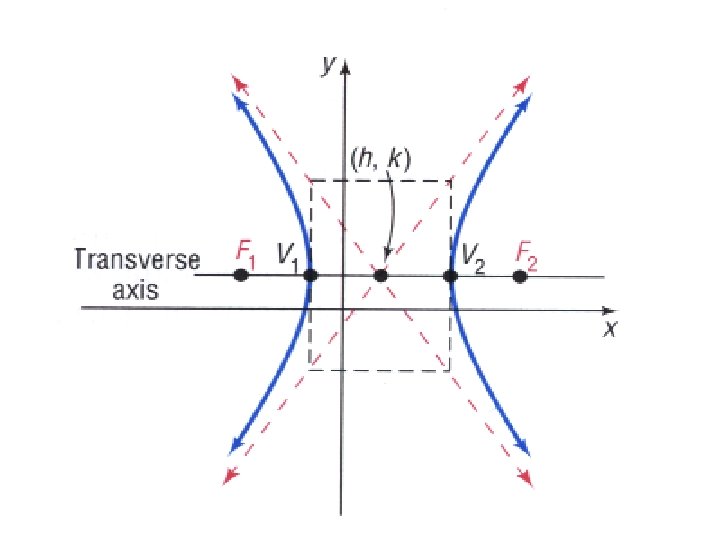
Hyperbola with Transverse Axis Parallel to the y-Axis; Center at (h, k) where b 2 = c 2 - a 2.

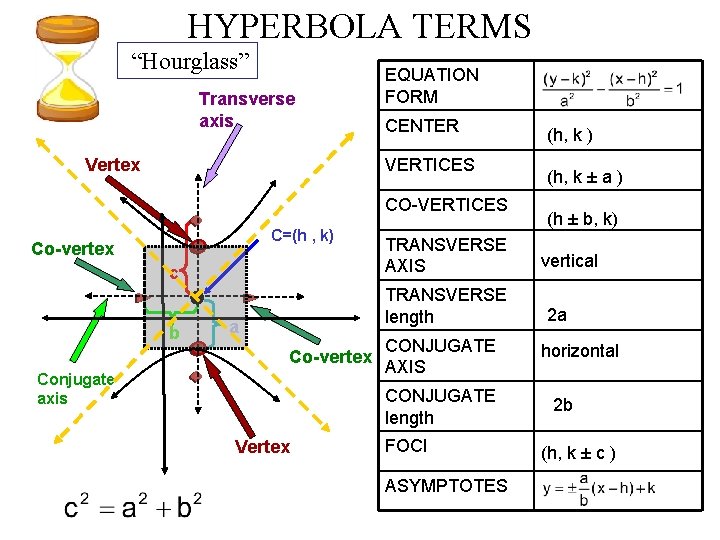
HYPERBOLA TERMS “Hourglass” Transverse axis Vertex EQUATION FORM CENTER VERTICES CO-VERTICES C=(h , k) Co-vertex c b TRANSVERSE AXIS TRANSVERSE length a Co-vertex Conjugate axis CONJUGATE AXIS CONJUGATE length Vertex FOCI ASYMPTOTES (h, k ) (h, k ± a ) (h ± b, k) vertical 2 a horizontal 2 b (h, k ± c )

Summary • If x term is positive, hyperbola opens left & right • If y term is positive, hyperbola opens up & down • a is always the positive 2 denominator

1. 2. 3. 4. Questions to ask yourself: What is the orientation of the hyperbola? What is the center (h, k)? What is “a” (the distance from the center to the vertex)? What is “b”? (use whatever information you can to find “b”)

Write the equation of the hyperbola given… • • • Draw a graph with given info Use given info to get measurement Find the center first Center is in middle of vertices, so (h , k) = (0 , 2) A = distance from center to vertices, so a = 5 Also, the conjugate length = 2 b Since conjugate = 12 Then b = 6 Use standard form • • Need values for h, k, a and b We know a = 5 and b = 6 The center is (0, 2) Plug into formula A = (-5, 2) major conjugate vertices are at (-5, 2) and (5, 2) conjugate axis of length 12 B = (5, 2)

Write the equation of the hyperbola given… center is at (-3, 2) foci at (-3, 2± 13) and major axis is 10 • • Draw a graph with given info Use given info to get measurements Find the center first Center is in middle of vertices, so (h , k) = (0 , 2) A = distance from center to vertices, so a = 5 We still don’t have b …. • • • Use the formula c² = a² + b² Since a = 5 and c = 13 then…. b = 12 (pythagorean triplet) F(-3, 2+13) Use standard form • • • Need values for h, k, a and b We know a = 5 and b = 12 and center is (0, 2) Plug into formula F(-3, 2 -13)

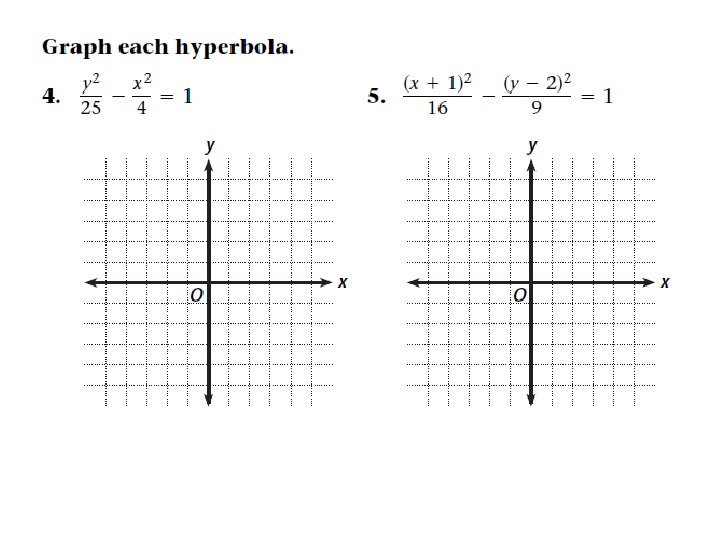
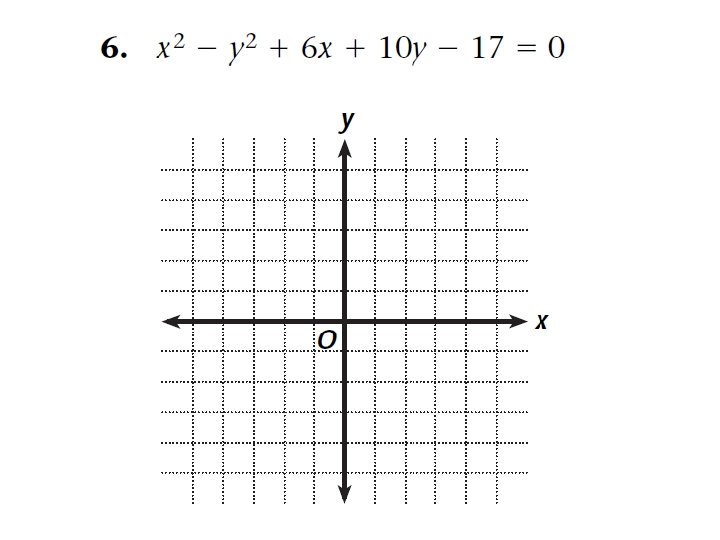
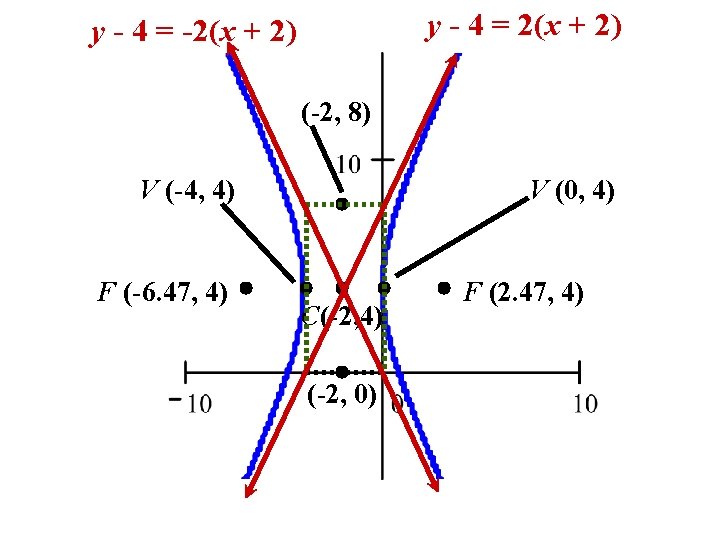
Find the center, transverse axis, vertices, foci, and asymptotes of

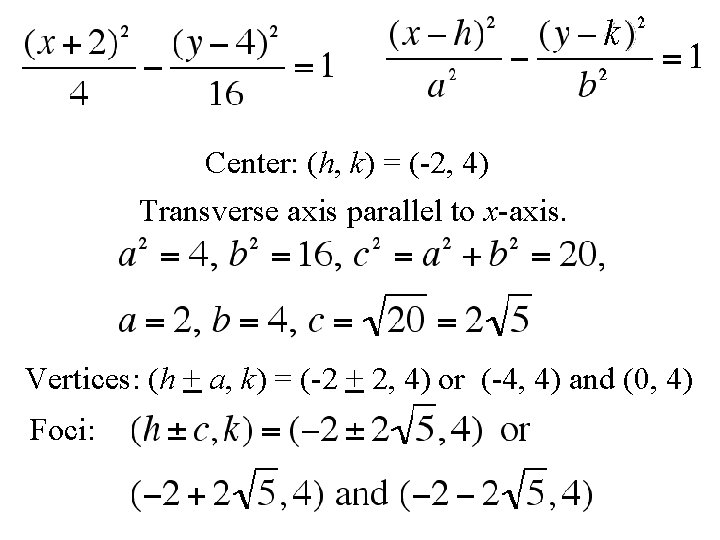
Center: (h, k) = (-2, 4) Transverse axis parallel to x-axis. Vertices: (h + a, k) = (-2 + 2, 4) or (-4, 4) and (0, 4) Foci:

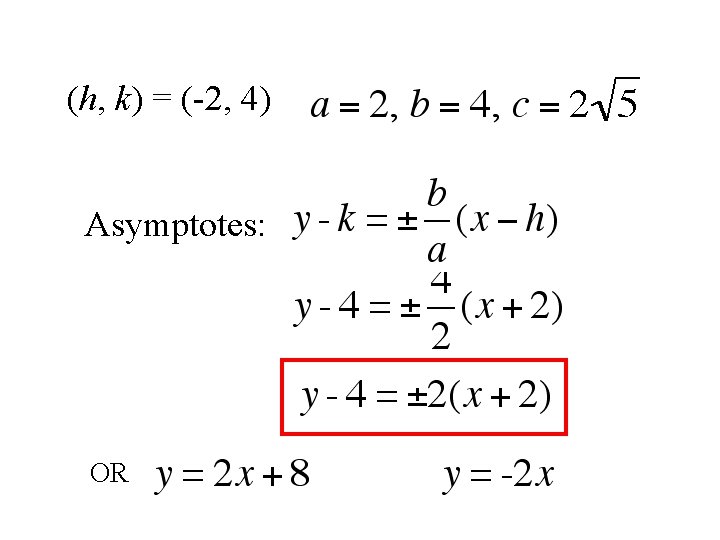
(h, k) = (-2, 4) Asymptotes: OR