The Hopf Bifurcation and the Brusselator Connor Smith

The Hopf Bifurcation and the Brusselator Connor Smith and Oliver Morfin December 3, 2010

Outline • Hopf Bifurcation – Limit Cycle – Conditions • The Jacobian Matrix • The T-D Plane • The Brusselator – Proof – Phase portraits • Conclusion 2

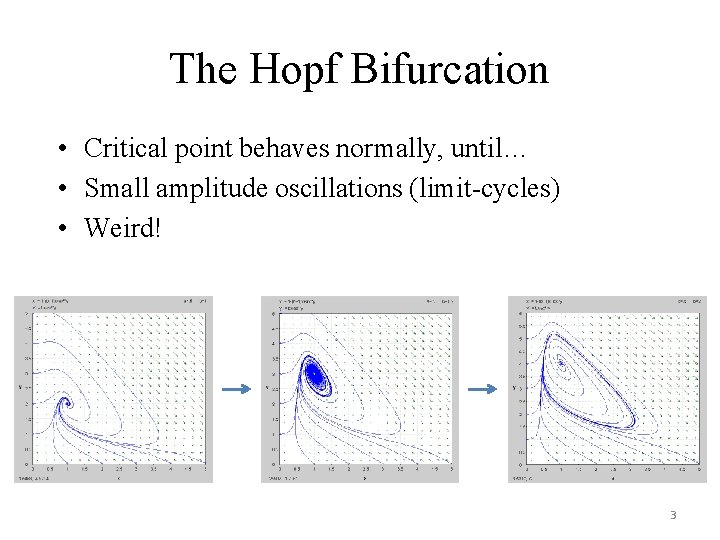
The Hopf Bifurcation • Critical point behaves normally, until… • Small amplitude oscillations (limit-cycles) • Weird! 3

A Limit Cycle • Closed trajectory in phase space • Solution curves converge and become periodic selfsustained oscillations • Example: Van der Pol Oscillator Image: http: //www. wolframalpha. com/entities/calculators/van_der_Pol_oscillator/ov/bm/om/ 4

The Jacobian Matrix • Non-linear system of differential equations: • Linearize by finding the Jacobian at the critical point: • Get the eigenvalues: 5

Using the Trace-Determinant Plane • When α = αH, two conditions must be true: 1. The TJ = 0 & DJ > 0 and, 2. The real part of the eigenvalues satisfy the condition: • Hopf bifurcation! Image: http: //www. math. sunysb. edu/~scott/Book 331/Fixed_Point_Analysis. html 6

The Brusselator • Autocatalytic chemical reaction sequence: • Rate equations: 7

First We Computed • Equilibrium point: • Jacobian matrix: • Trace & Determinant: 8

Then… • Hopf bifurcation TJ = 0 & DJ > 0 • a > 0 and b >0 – Therefore DJ = a > 0, as required. – • Since the system only has one equilibrium point a Hopf bifurcation occurs when. • To prove that we have a Hopf bifurcation, there are two conditions… 9

Condition #1 • Eigenvalues of zero at. – λ’s of are purely imaginary and non- are imaginary T 2 - 4 D <0 – We know: – Given TJ =0, and – Thus T disappears as required. 10

Condition #2 • The rate of change of the real part is greater than zero at. • For any eigenvalue λ, • Since a is a fixed constant: Thus, by #1 and #2, a Hopf bifurcation occurs at 11

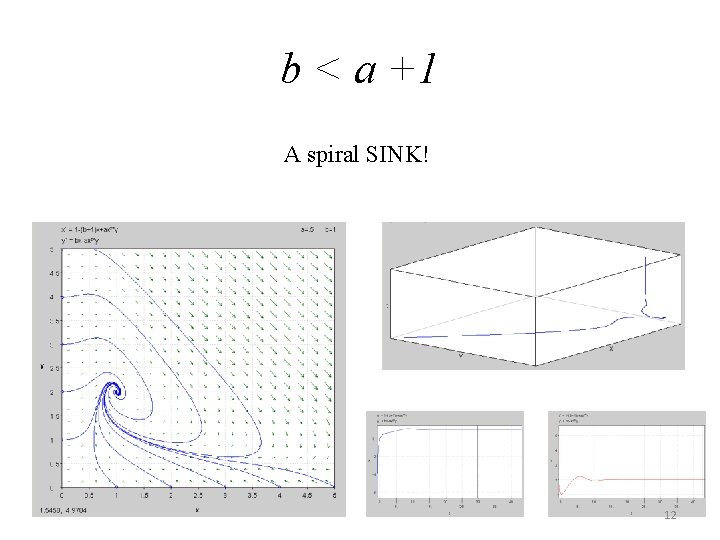
b < a +1 A spiral SINK! 12

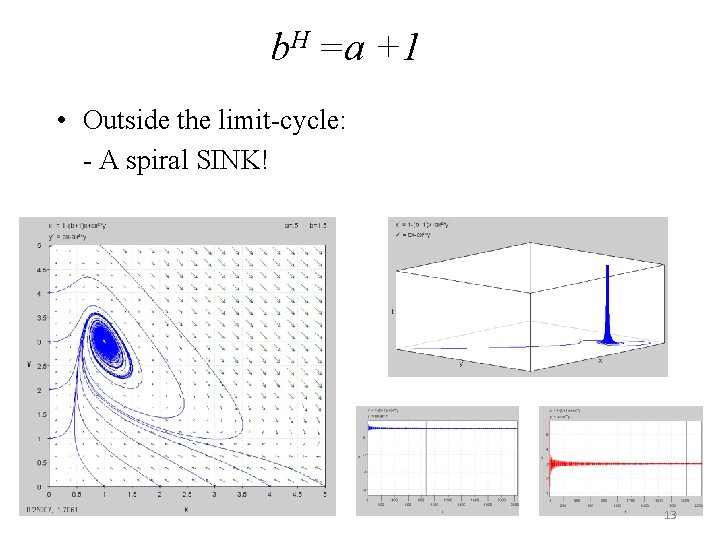
b. H =a +1 • Outside the limit-cycle: - A spiral SINK! 13

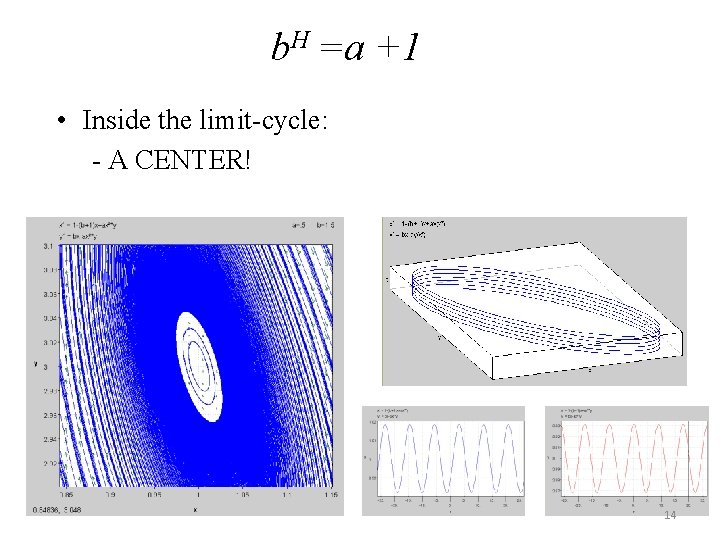
b. H =a +1 • Inside the limit-cycle: - A CENTER! 14

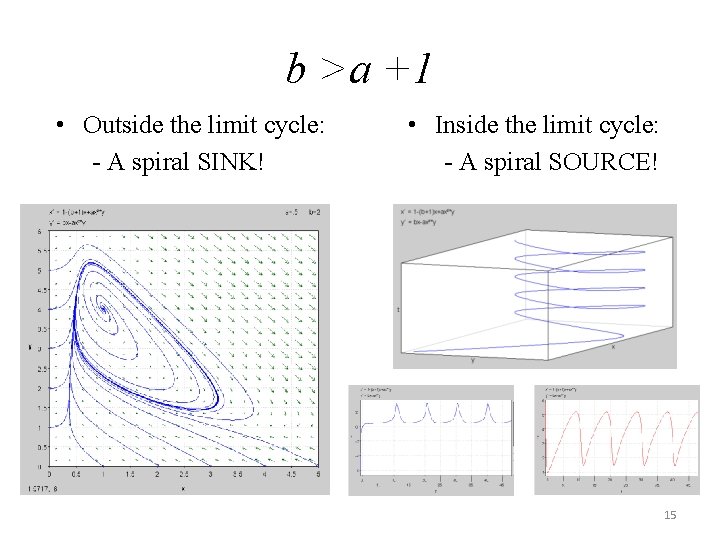
b >a +1 • Outside the limit cycle: - A spiral SINK! • Inside the limit cycle: - A spiral SOURCE! 15

Conclusion • Characteristics of a Hopf bifurcation • How to find and determine the properties of a Hopf bifurcation • Analysis of the Brusselator’s Hopf bifurcation 16

References • Arrowsmith, D. K. , and C. M. Place. Ordinary Differential Equations: A Qualitative Approach with Applications. London: Chapman and Hall, 1982. • Ault, Shaun; Holmgreen, Erik. “Dynamics of the Brusselator” Academia. edu, 16 March 2003. 11/27/10 <http: //fordham. academia. edu/Shaun. Ault/Papers/83373/Dynamics_of_the_ Brusselator> • Franke, Reiner. "A Precise Statement of the Hopf Bifurcation Theorem and Some Remarks. " 1 -6 pp. • <http: //www. bwl. uni-kiel. de/gwif/files/handouts/dmt/Hopf. Precise. pdf>. • Guckenheimer, John; Myers, Mark; and Sturmfels, Bernd. "Computing Hopf Bifurcations I. " Society for Industrial and Applied Mathematics Journal on Numerical Analysis 34 (1997): 1 -21 pp. 11/11/10 <http: //www. jstor. org/stable/2952033>. • Kuznetsov, Yuri A. "Andronov-Hopf Bifurcation. " Scholarpedia, 2006. • Pernarowski, Mark. "Hopf Bifurcations - an Introduction. " Montana State University, 2004. 1 -2. • Wiens, Elmer G. "Bifurcations and Two Dimensional Flows. " Egwald Mathematics. • Graphs were created using PPlane (math. rice. edu/~dfield/dfpp. html) 17