The Helical Luttinger Liquid and the Edge of

The Helical Luttinger Liquid and the Edge of Quantum Spin Hall Systems Congjun Wu Kavli Institute for Theoretical Physics, UCSB B. Andrei Bernevig, and Shou-Cheng Zhang Physics Department, Stanford University Ref: C. Wu, B. A. Bernevig, and S. C. Zhang, Phys. Rev. Lett. 96, 106401 (2006). March Meeting, 03/15/2006, 3: 42 pm. 1

Introduction • Spin Hall effect (SHE): Use electric field to generate transverse spin current in spin-orbit (SO) coupling systems. S. Murakami et al. , Science 301 (2003); J. Sinova et al. PRL 92, 126603 (2004). Y. Kato et al. , PRL 93, 176001 (2004); J. Wunderlich et al. PRL 94, 47204 (2005). • Quantum SHE systems: bulk is gapped; no charge current. • Gapless edge modes support spin transport. F. D. M. Haldane, PRL 61, 2015 (1988); Kane et al. , cond-mat/0411737, Phys. Rev. Lett. 95, 146802 (2005); B. A. Bernevig et al. , cond-mat/0504147, to appear in PRL; X. L Qi et al. , condmat/0505308; L. Sheng et al. , PRL 95, 136602 (2005); D. N. Sheng et al, cond-mat/0603054. • Stability of the gapless edge modes against impurity, disorder under strong interactions. C. Wu, B. A. Bernevig, and S. C. Zhang, cond-mat/0508273, to appear in Phys. Rev. Lett; C. Xu and J. Moore, PRB, 45322 (2006). 2

QSHE edges: Helical Luttinger liquids (HLL) • Edge modes are characterized by helicity. • Right-movers with spin up, and left-movers with spin down: • n-component HLL: n-branches of time-reversal pairs (T 2=-1). upper edge lower edge • HLL with an odd number of components are special. chiral Luttinger liquids in quantum Hall edges break TR symmetry; spinless non-chiral Luttinger liquids: T 2=1; non-chiral spinful Luttinger have an. Wu even number of Kaneliquids et al. , PRL 2005, et al. , PRL 2006. branches of TR pairs. 3

The no-go theorem for helical Luttinger liquids • 1 D HLL with an odd number of components can NOT be constructed in a purely 1 D lattice system. E EF -p • Double degeneracy occurs at k=0 and p. • Periodicity of the Brillouin zone. p • HLL with an odd number of components can appear as the edge states of a 2 -D system. H. B. Nielsen et al. , Nucl Phys. B 185, 20 (1981); C. Wu et al. , Phys. Rev. Lett. 96, 106401 (2006). 4

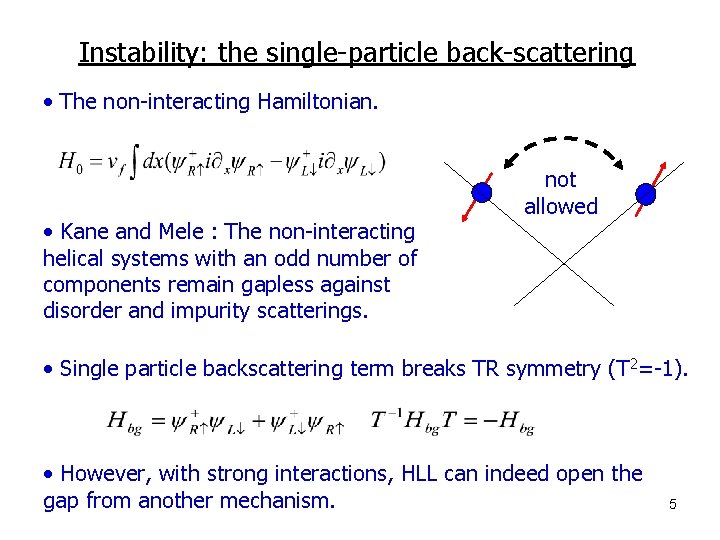
Instability: the single-particle back-scattering • The non-interacting Hamiltonian. • Kane and Mele : The non-interacting helical systems with an odd number of components remain gapless against disorder and impurity scatterings. not allowed • Single particle backscattering term breaks TR symmetry (T 2=-1). • However, with strong interactions, HLL can indeed open the gap from another mechanism. 5

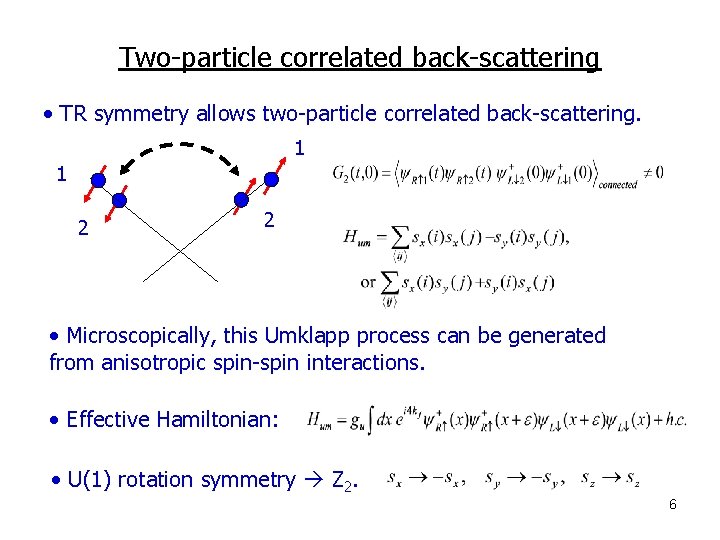
Two-particle correlated back-scattering • TR symmetry allows two-particle correlated back-scattering. 1 1 2 2 • Microscopically, this Umklapp process can be generated from anisotropic spin-spin interactions. • Effective Hamiltonian: • U(1) rotation symmetry Z 2. 6

Bosonization+Renormalization group • Sine-Gordon theory at kf=p/2. • If K<1/2 (strong repulsive interaction), the gap D opens. Order parameters 2 kf SDW orders Nx (gu<0) or Ny at (gu>0). • TR symmetry is spontaneously broken in the ground state. • At , TR symmetry much be restored by thermal fluctuations and the gap remains. 7

Random two-particle back-scattering • Scattering amplitudes variables. are quenched Gaussian Giamarchi, Quantum physics in one dimension, oxford press (2004). • If K<3/8, gap D opens. SDW order is spatially disordered but static in the time domain. • TR symmetry is spontaneously broken. • At small but finite temperatures, gap remains but TR is restored by thermal fluctuations. 8

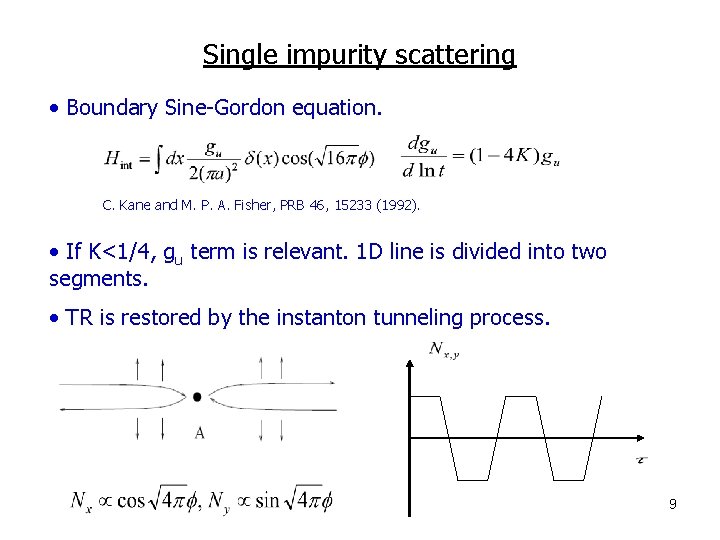
Single impurity scattering • Boundary Sine-Gordon equation. C. Kane and M. P. A. Fisher, PRB 46, 15233 (1992). • If K<1/4, gu term is relevant. 1 D line is divided into two segments. • TR is restored by the instanton tunneling process. 9

Kondo problem: magnetic impurity scattering • Poor man RG: critical coupling Jz is shifted by interactions. • If K<1 (repulsive interaction), the Kondo singlet can form with ferromagnetic couplings. 10

Summary • Helical Luttinger liquid (HLL) as edge states of QSHE systems. • No-go theorem: HLL with odd number of components can not be constructed in a purely 1 D lattice system. • Instability problem: Two-particle correlated back-scattering is allowed by TR symmetry, and becomes relevant at: Kc<1/2 for Umklapp scattering at commensurate fillings. Kc<3/8 for random disorder scattering. Kc<1/4 for a single impurity scattering. • Critical Kondo coupling Jz is shifted by interaction effects. 11