The Greedy Algorithm for Edit Distance with Moves

Edit Distance Minimum Number of: • Character insertions • Character deletions • Character changes

Edit Distance with Moves Minimum Number of: • Character insertions • Character deletions •

Known Results • Problem is NP-Hard (Shapira, Storer) • OPT lognlog*n – appoximation (Cormode

Minimum Common String Partition Problem (MCSP) |S| = |T| - S and T contain

Edit Dsitance and Moves and MCSP (Shapira, Storer) 1. OPTMCSP(S, T) ≤ 3 OPTEDM(S,

OPTMCSP(S, T) ≤ 3 OPTEDM(S, T)+1 Every move adds at most 3 blocks to

OPTMCSP(S, T) ≤ 3 OPTEDM(S, T)+1 Given an instance of MCSP Solve the EDM

Reduction into Move only Operations S = abcae T = abcd S 1 =

OPTEDM(S, T) ≤ OPTMCSP(S’, T’) -1 Reduce into move only sequence: We get to

Greedy Algorithm for MCSP Mark identical disjoint blocks of maximum size S = abcbabcdcb

Greedy Algorithm for MCSP Chorbak et. al. Greedy = (|S|0. 43 OPT) - |Σ|

(n 0. 43 OPT) Bound for GREEDY A 0 =a B 0 =

(n 0. 43 OPT) Bound for GREEDY Ai = Ai-1 Bi-1 Ci-1 Bi-1

(n 0. 46 OPT) Bound for GREEDY Ai = Bi-1 Ai-1 Ci-1 Ai-1

Open Problems • Get a better bound on the performance ratio of Greedy (sqrt(n)

Slides: 27

Download presentation

The Greedy Algorithm for Edit Distance with Moves Nira Shafrir – Tel Aviv University Joint with: Haim Kaplan – Tel Aviv University

Edit Distance Minimum Number of: • Character insertions • Character deletions • Character changes To convert S into T Can be Computed using DP in O(|S||T|) S = abcde f S 1 = bcde T = bcfeg S 2 = bcfeg

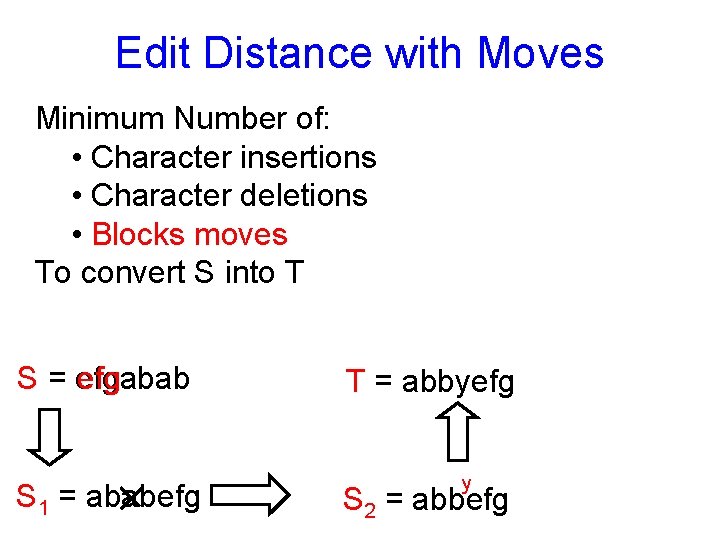
Edit Distance with Moves Minimum Number of: • Character insertions • Character deletions • Blocks moves To convert S into T S = efgabab efg S 1 = ababefg T = abbyefg y S 2 = abbefg

Known Results • Problem is NP-Hard (Shapira, Storer) • OPT lognlog*n – appoximation (Cormode Muthukrishnan) • Shapira and Storer – Edit distance with moves can be reduced to the Minimum Common String Partition Problem (MCSP)

Minimum Common String Partition Problem (MCSP) |S| = |T| - S and T contain the same multiset of characters. Find minimum partition into identical disjoint blocks S = abccbdau T = aucbdabc

Edit Dsitance and Moves and MCSP (Shapira, Storer) 1. OPTMCSP(S, T) ≤ 3 OPTEDM(S, T)+1 2. OPTEDM(S, T) = OPTEDM(S’, T’) ≤ OPTMCSP(S’, T’)-1

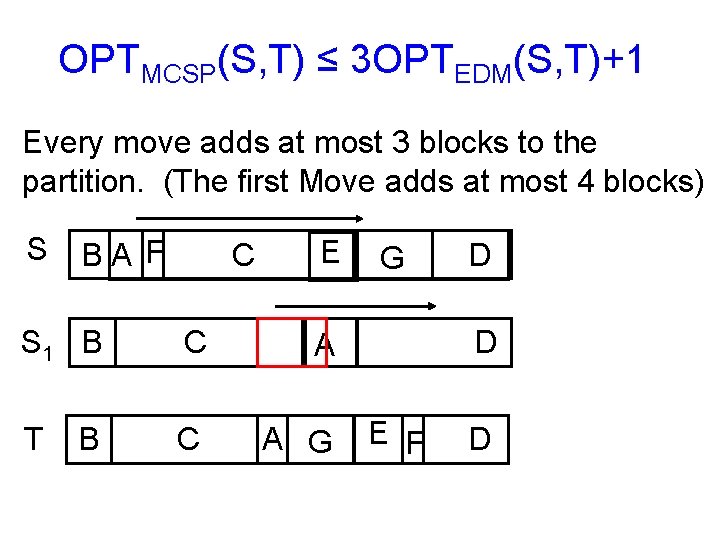
OPTMCSP(S, T) ≤ 3 OPTEDM(S, T)+1 Every move adds at most 3 blocks to the partition. (The first Move adds at most 4 blocks) S BA F C E S 1 B C A T C A G B G D D E F D

OPTMCSP(S, T) ≤ 3 OPTEDM(S, T)+1 Every move adds at most 3 blocks to the partition. (The first Move adds at most 4 blocks) S = xababycddcz a S 1 =xabbaycddcz y S 2 =xabbacddcyz abba T =xcddcyabbaz

OPTMCSP(S, T) ≤ 3 OPTEDM(S, T)+1 Every move adds at most 3 blocks to the partition. (The first Move adds at most 4 blocks) S = xababycddcz a S 1 =xabbaycddcz y S 2 =xabbacddcyz abba T =xcddcyabbaz S = xababycddcz T =xcddcyabbaz

OPTMCSP(S, T) ≤ 3 OPTEDM(S, T)+1 Given an instance of MCSP Solve the EDM problem. The solution AEDM defines a solution BMCSP for MCSP. |BMCSP| ≤ 3|AEDM|+1 OPTMCSP ≤ 3 OPTEDM+1

OPTEDM(S, T) ≤ OPTMCSP(S’, T’) -1

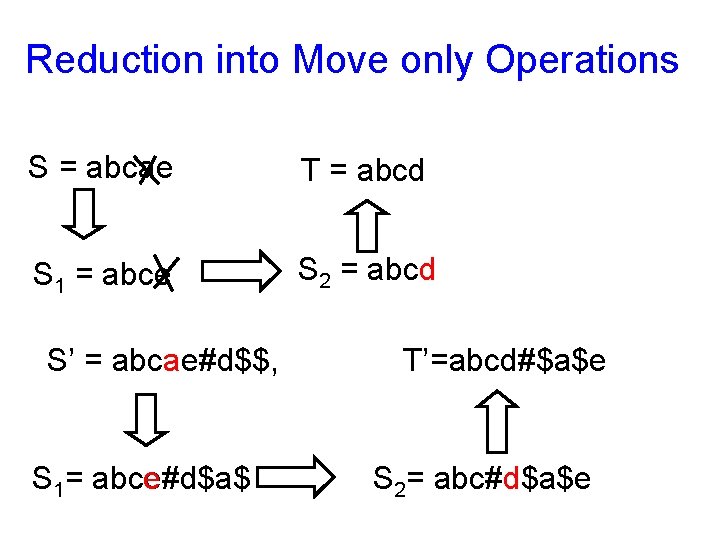
Reduction into Move only Operations S = abcae T = abcd S 1 = abce S 2 = abcd S’ = abcae#d$$, a S 1= abce#d$a$ e T’=abcd#$a$e S 2= abc#d$a$e d

OPTEDM(S, T) ≤ OPTMCSP(S’, T’) -1 Reduce into move only sequence: We get to strings S’, T’ with the same multiset of characters Solve MCSP(S’, T’) Number of Moves ≤ Number of Blocks -1 (Worst case: S’=abcd, T’=dcba (3 moves)) OPTEDM ≤ OPTMCSP -1

Greedy Algorithm for MCSP Mark identical disjoint blocks of maximum size S = abcbabcdcb T = bcdcbabcba S = abcbabcdcb T = bcdcbabcbc

Greedy Algorithm for MCSP Chorbak et. al. Greedy = (|S|0. 43 OPT) - |Σ| = |S|0. 43 Greedy = O(|S|0. 69 OPT) Our result: Greedy = (|S|0. 46 OPT) - |Σ| = O(log n)

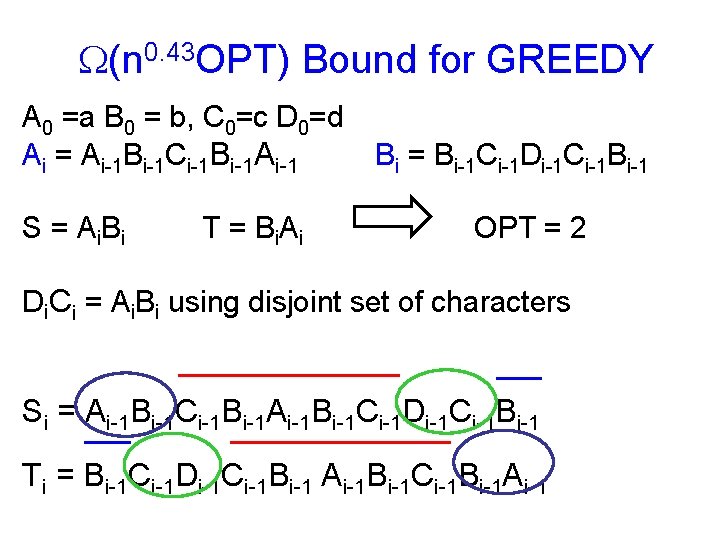
(n 0. 43 OPT) Bound for GREEDY A 0 =a B 0 = b, C 0=c D 0=d Ai = Ai-1 Bi-1 Ci-1 Bi-1 Ai-1 S = A i. B i T = B i. A i Bi = Bi-1 Ci-1 Di-1 Ci-1 Bi-1 OPT = 2 Di. Ci = Ai. Bi using disjoint set of characters Si = Ai-1 Bi-1 Ci-1 Bi-1 Ai-1 Bi-1 Ci-1 Di-1 Ci-1 Bi-1 Ti = Bi-1 Ci-1 Di-1 Ci-1 Bi-1 Ai-1 Bi-1 Ci-1 Bi-1 Ai-1

(n 0. 43 OPT) Bound for GREEDY Ai = Ai-1 Bi-1 Ci-1 Bi-1 Ai-1 Bi = Bi-1 Ci-1 Di-1 Ci-1 Bi-1 Si = Ai-1 Bi-1 Ci-1 Bi-1 Ai-1 Bi-1 Ci-1 Di-1 Ci-1 Bi-1 Ti = Bi-1 Ci-1 Di-1 Ci-1 Bi-1 Ai-1 Bi-1 Ci-1 Bi-1 Ai-1 R(i) = number of blocks GREEDY finds on Si, Ti R(i) = 2 + 2 R(i-1) = 2 i n = |Si| = 5|Si-1| = 2*5 i 2 i i log 2 5 5 R(i) = = = 5 ilog 52 = nlog 52 |Σi| = 2| Σi-1| = 2 i = n 0. 43

(n 0. 43 OPT) Bound for GREEDY Ai = Ai-1 Bi-1 Ci-1 Bi-1 Ai-1 Bi = Bi-1 Ci-1 Di-1 Ci-1 Bi-1 S 1 = abcbabcdcb T 1 = bcdcbabcba A 1 = abcba B 1 = bcdcb C 1 = fghgf D 1 = efgfe A 1 B 1 C 1 B 1 A 1 B 1 C 1 D 1 C 1 B 1 S 2 = abcbabcdcbfghgfbcdcbabcba bcdcbfghgfefghgfbcdcb T 2 = bcdcbfghgfefghgfbcdcb abcbabcdcbfghgfbcdcbabcba

Improving the Lower Bound for Greedy

(n 0. 46 OPT) Bound for GREEDY Ai = Bi-1 Ai-1 Ci-1 Ai-1 Bi-1 S i = A i. B i T i = B i. A i Bi = Ai-1 Ci-1 di. Ci-1 Ai-1 OPT = 2 Ci = Ai-1 Ci-1 ei. Ci-1 Ai-1 di 2 new symbols |Ci| = |Bi| Si = Bi-1 Ai-1 Ci-1 Ai-1 Bi-1 Ai-1 Ci-1 di. Ci-1 Ai-1 Ti = Ai-1 Ci-1 di. Ci-1 Ai-1 Bi-1 Ai-1 Ci-1 Ai-1 Bi-1

(n 0. 46 OPT) Bound for GREEDY Ai = Bi-1 Ai-1 Ci-1 Ai-1 Bi-1 Bi = Ai-1 Ci-1 di. Ci-1 Ai-1 Si = Bi-1 Ai-1 Ci-1 Ai-1 Bi-1 Ai-1 Ci-1 di. Ci-1 Ai-1 Ti = Ai-1 Ci-1 di. Ci-1 Ai-1 Bi-1 Ai-1 Ci-1 Ai-1 Bi-1 Ci = Ai-1 Ci-1 ei. Ci-1 Ai-1 ei, di 2 new symbols |Ci| = |Bi|≤|Ai|, ½|Si| |Ai| = 2|Ai-1| + 3|Bi-1| |Bi| = |Ci| = 2|Ai-1|+2|Bi-1| +1 |Ci-1 Ai-1 Bi-1 Ai-1 Ci-1| = 2|Ai-1| + 3|Bi-1| = |Ai| Largest common blocks Ai, Ci-1 Ai-1 Bi-1 Ai-1 Ci-1

(n 0. 46 OPT) Bound for GREEDY Ai = Bi-1 Ai-1 Ci-1 Ai-1 Bi-1 Bi = Ai-1 Ci-1 di. Ci-1 Ai-1 Si = Bi-1 Ai-1 Ci-1 Ai-1 Bi-1 Ai-1 Ci-1 di. Ci-1 Ai-1 Ti = Ai-1 Ci-1 di. Ci-1 Ai-1 Bi-1 Ai-1 Ci-1 Ai-1 Bi-1 Ci = Ai-1 Ci-1 ei. Ci-1 Ai-1 ei, di 2 new symbols |Ci| = |Bi|≤|Ai|, ½|Si| n= |Si| =|Ai| +|Bi| = 4|Ai-1| + 5|Bi-1| + 1 = 4(|Ai-1 I+|Bi-1|)+|Bi-1| + 1 ≤ 4. 5|Si-1| +1 = 4. 5 i |Σi| = 2 + | Σi-1| = 2 i = O(log n)

(n 0. 46 OPT) Bound for GREEDY Ai = Bi-1 Ai-1 Ci-1 Ai-1 Bi-1 Bi = Ai-1 Ci-1 di. Ci-1 Ai-1 Si = Bi-1 Ai-1 Ci-1 Ai-1 Bi-1 Ai-1 Ci-1 di. Ci-1 Ai-1 Ti = Ai-1 Ci-1 di. Ci-1 Ai-1 Bi-1 Ai-1 Ci-1 Ai-1 Bi-1 n= |Si| = 4. 5 i R(i) = number of blocks GREEDY finds on Si, Ti R(i) = 2 + 2 R(i-1) = 2 i R(i) = 2 i = 4. 5 log 4. 52 i = 4. 5 ilog 4. 52 = n 0. 46 |

(n 0. 46 OPT) Bound for GREEDY Ai = Bi-1 Ai-1 Ci-1 Ai-1 Bi-1 Bi = Ai-1 Ci-1 di. Ci-1 Ai-1 S 1 = bacabacdca T 1 = acdcabacab A 1 = bacab B 1 = acdca C 1 = aceca B 1 A 1 C 1 A 1 B 1 A 1 C 1 d 2 C 1 A 1 S 2 = acdcabacecabacdca bacabacecagacecabacab T 2 = bacabacecagacecabacab acdcabacecabacdca

(n 0. 46 OPT) Bound for GREEDY Ai = Bi-1 Ai-1 Ci-1 Ai-1 Bi-1 S 1 = bacabacdca Bi = Ai-1 Ci-1 di. Ci-1 Ai-1 A 1 = bacab, B 1= acdca T 1 = acdcabacab A 1 = bacab B 1 = acdca C 1 = aceca B 1 A 1 C 1 A 1 B 1 A 1 C 1 d 2 C 1 A 1 S 2 = acdcabacecabacdca bacabacecagacecabacab T 2 = bacabacecagacecabacab acdcabacecabacdca A 1 C 1 d 2 C 1 A 1 B 1 A 1 C 1 A 1 B 1

Open Problems • Get a better bound on the performance ratio of Greedy (sqrt(n) ? ) • Is there a constant approximation for the problems? • Try to get O(log n) approximation for MCSP (and for Edit distance with moves)