The Greatest Unsolved Problem in Mathematics Part 2

The Greatest Unsolved Problem in Mathematics Part 2 The Riemann hypothesis Are all the zeta function zeroes on the ‘halfline’ ? Who cares?

We care! Researchers suspect that proving the RH may reveal new techniques that would affect factoring and cryptography. Parts of modern cryptography such as key exchange and digital signatures assume that factoring large numbers is a ‘hard problem’ … too hard for all the computing power in the world. Links between zeta zeroes and the physics of the quantum world would be revealed. More on this later… Just because … The Universe is telling us something beautiful about numbers and primes. Although we may not know what the question is (with apologies to Douglas Adams). Mathematicians, computer scientists, statisticians and physicists would get to party hard. And someone will win the $1, 000 Clay prize (more on that later).

There are two way of attacking the Riemann hypothesis Brain power Raw power Anything else you can think of…

Some quick mental preparation EXCURSION Large Numbers

million (mega) billion (giga) World population ~ 7. 65 billion trillion (tera) About 2 trillion observable galaxies quadrillion (peta) Total insects on Earth ~ 10 quintillion Estimated number of atoms in the Earth Number of different shuffles of a 52 card deck (for comparison) Number of atomic particles in the observable universe (low estimate) Numbers without names Physical comparisons become impossible after this point. A googol (not an official name) Towers of Powers Number of books in Jorge Luis Borges' Library of Babel EXCURSION Stars in the observable Universe Molecules in a glass of water septillion (yotta) Number of ants on Earth quintillion (exa) Numbers with names Grains of sand in the jar

Other Interesting Numbers Total internet traffic in 2016 1. 2 zetabytes Total data stored 250 exabytes Sun’s power 386 yotawatt The human heart → 3 to 4 watt Eurostar electric locomotive → 12, 000 watt Belgian Doel Nuclear Power Station → 1, 040, 000 watt Human energy consumption 2013 → 18, 000, 000 watt/hour EXCURSION

Brain Power

The Greatest Unsolved Problem in Mathematics After Riemann’s 1859 paper… Nothing much happens for 35 years. The 20 th century brings a new generation of ‘middle players’

1896 — The Prime Number Theorem is Proved Breakthrough Jacques Hadamard and Charles Jean de la Vallée Poussin independently prove the Prime Number Theorem about 100 years after Legendre and Gauss stated it. 1890 s Party!

1900 – Hilbert’s 23 Problems David Hilbert presented ten of twenty three problems (1, 2, 6, 7, 13, 16, 19, 21, 22) at the Paris International Congress of Mathematicians, speaking on August 8 th in the Sorbonne.

Hardy–Littlewood Godfrey Harold Hardy 1877– 1947 John Edensor Littlewood 1885– 1977 Srinivasa Ramanujan 1887– 1920 Played by Jeremy Irons, Toby Jones and Dev Patel in the 2015 movie The Man Who Knew Infinity

An angle of attack … How ‘dense’ are the zeroes on the line? Try to prove that more and more zeroes are on the line, until they are so ‘dense’ that there’s no room left for exceptions off the line.

Some progress on ‘density’ 1914 Hardy proves there are infinitely many zeroes on the line. 1921 Hardy-Littlewood prove there are k. T zeroes on the line. 1942 Atle Selberg improves the previous result to k. T log T. Each result proves the zeroes on the line are more ‘dense’ than the previous one, but sadly it’s hopelessly inadequate to prove they’re all on the line. In fact, an infinite number might still be off the line.

Some progress on ‘density’ 1974 Norman Levinson proves 1/3 of zeroes are on the line. 1989 John Brian Conrey proves 2/5 of zeroes are on the line This is still a long way from 100% on the line. …relative to time scales in this presentation

Another angle of attack … Can we narrow the strip? All zeroes must be in the strip 0 to 1. Can we narrow the strip containing them down until it’s so thin that there’s no room for exceptions off the line? 0 ½ 1

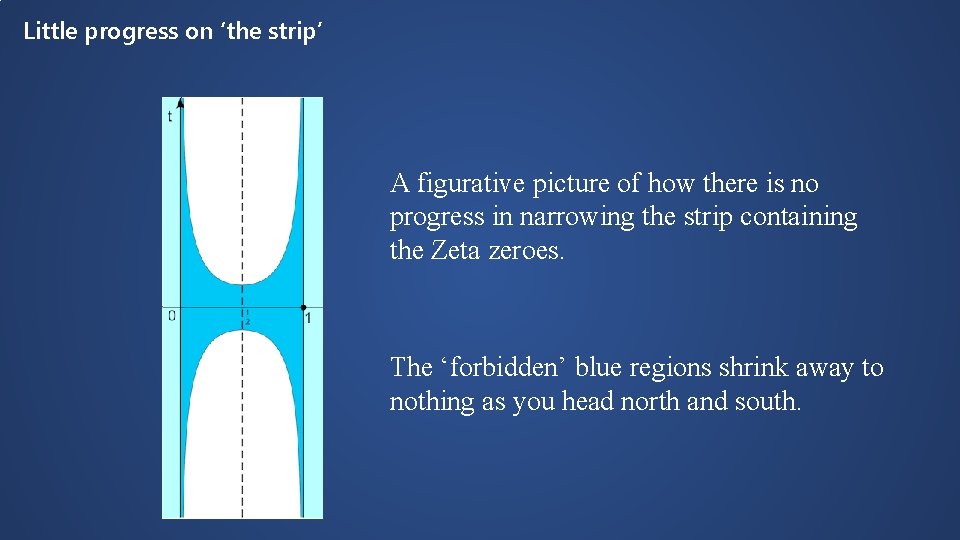
Little progress on ‘the strip’ A figurative picture of how there is no progress in narrowing the strip containing the Zeta zeroes. The ‘forbidden’ blue regions shrink away to nothing as you head north and south.

The ‘Brain Power’ People Dirichlet 1805– 1859 Hilbert 1862– 1943 Turing 1912– 1954 de la Vallée Poussin Hadamard 1866– 1862 1865– 1963 Landau 1877– 1938 Artin 1898– 1962 Hardy 1877– 1947 Weil 1906– 1998 Dedekind 1831– 1916 Chebyshev 1821– 1894 Gram 1850– 1916 Littlewood 1885– 1977 Selberg 1917– 2007 Siegel 1896– 1981 Bombier i 1940– Odlyzko 1949– Deligne 1944– Goldbach Riesel Zagier von Koch Ingham Möbius Mertens Lindelöf Polignac Titchmarsh Rosser Cramér Erdös Weintraub Brent Heath-Brown Jutila Turán Pomerance Montgomery Pólya Connes Turán de Branges Ivić Ishikawa Karatsuba

EXCURSION A sobering warning that hunches about numbers can be depressingly wrong

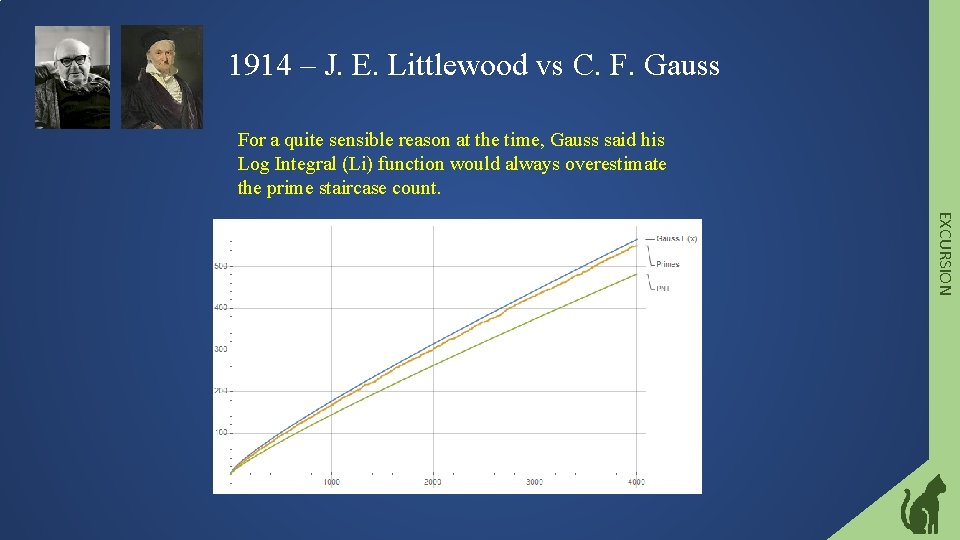
1914 – J. E. Littlewood vs C. F. Gauss For a quite sensible reason at the time, Gauss said his Log Integral (Li) function would always overestimate the prime staircase count. EXCURSION

Prime Count vs Log Integral As far as humanity has counted, Gauss’ Log Integral does overestimate the prime count. It was assumed that this trend would continue forever. EXCURSION The last prime count for 1027 was calculated in late 2018

Prime Count vs Log Integral Littlewood proved that the prime staircase swaps the lead with Log Integral infinitely often. Disproving a hunch by the legendary Gauss made Littlewood a mathematical celebrity. Mathematicians use this as evidence that prime numbers and the zeta zeroes ‘misbehave’ in strange ways as you head to vast distances far beyond our computing power. Littlewood couldn’t say where the first swap happens, so he asked his student Samuel Skewes to find where the first ‘Littlewood Violation’ occurred (or at least find an upper limit). EXCURSION Where is the first ‘Littlewood violation’, where the staircase exceeds Log Integral?

In 1933 Stanley Skewes proved that the first ‘Littlewood Violation’ occurred before these numbers Limit if the RH is false Luckily, the limit has been reduced to a more comprehensible value thanks to increasing computing power. Lehman – 1966 Hermanus te Riele – 1987 Bays and Hudson – 2000 Stoll and Demichel – 2011 ~ 1. 6 × 101165 ~ 7 × 10370 ~ 1. 4 × 10316 ~ 1. 397162 × 10316 Since an accurate prime count has only been calculated as far as 1027, the current violation point is far beyond humanity’s computing power. EXCURSION Limit if the RH is true

Raw Power

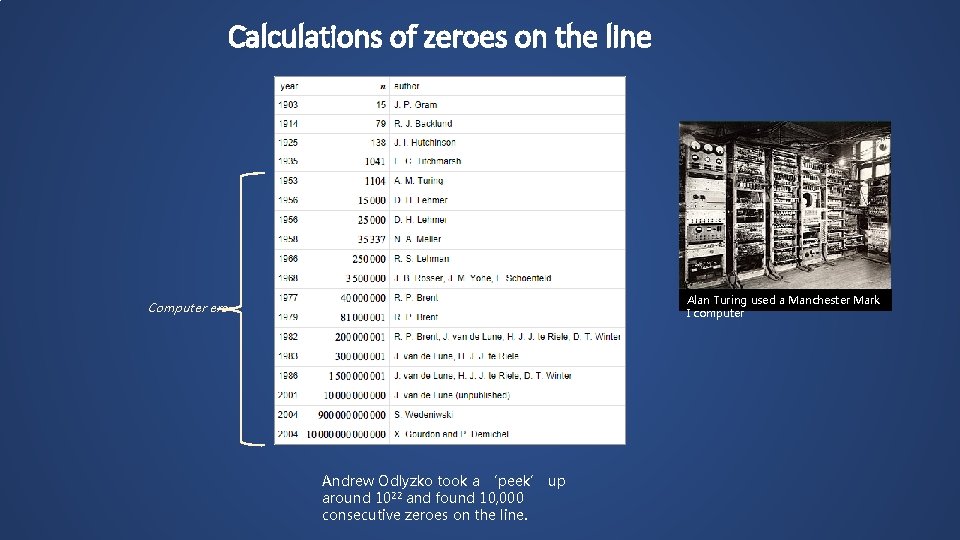
Calculations of zeroes on the line Alan Turing used a Manchester Mark I computer Computer era Andrew Odlyzko took a ‘peek’ up around 1022 and found 10, 000 consecutive zeroes on the line.

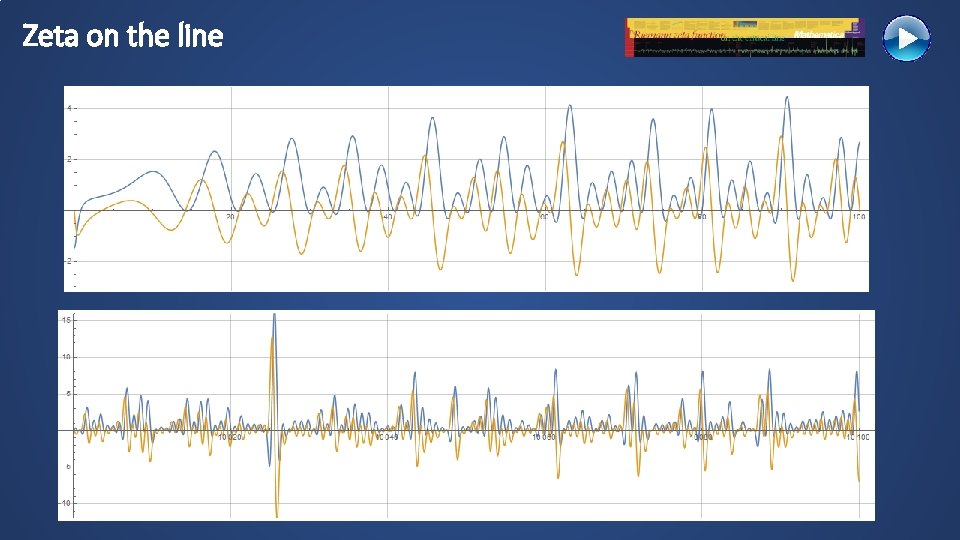
Zeta on the line

Do 10 trillion zeroes on the line help prove the Riemann hypothesis? NO Numerical evidence is worthless for a proof It’s not like coin tossing. Prime numbers are deceptive … they often hint that some theorem may be true, perhaps supported by vast numerical evidence, then as you look further you realise the numbers were lying. Many famous hunches have been demolished in the last 200 years. Remember Littlewood vs Gauss

Quantum Zeroes It gets a bit weird now…

Eugene Wigner 1902 – 1995 Freeman Dyson 1923– Max Planck 1858– 1947 George Polya 1887– 1985 Albert Einstein 1879 – 1955 Arthur Compton 1892 – 1962 The founders of quantum mechanics Quantum behaviour is a dynamical system so complex that it can only be described statistically. Physicists have been using a special technique for 100 years to model the quantum world. Uranium Physicists use…

The Matrix

No… The Matrix Matrices can represent and manipulate large amounts of information in a compact way Matrices have ‘zeroes’ They are called the eigenvalues of a matrix.

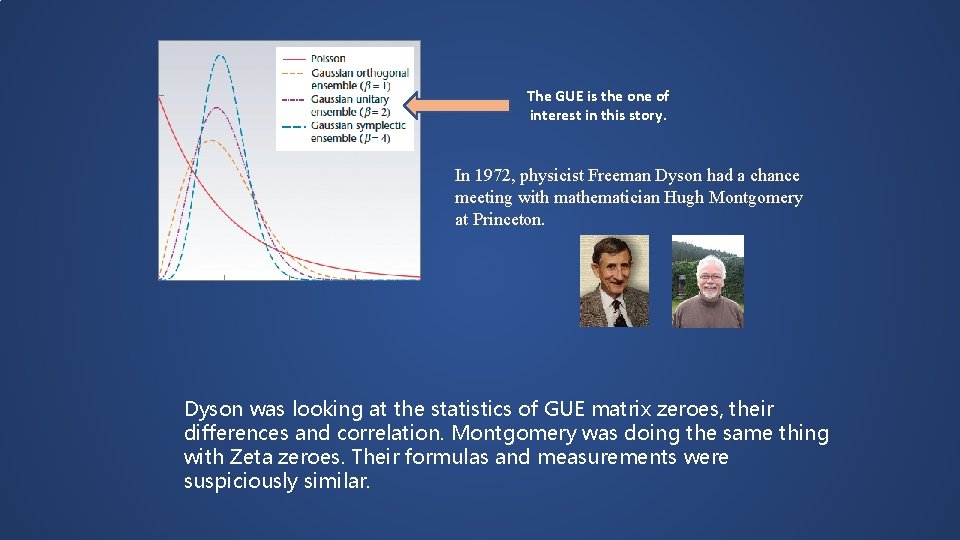
The GUE is the one of interest in this story. In 1972, physicist Freeman Dyson had a chance meeting with mathematician Hugh Montgomery at Princeton. Dyson was looking at the statistics of GUE matrix zeroes, their differences and correlation. Montgomery was doing the same thing with Zeta zeroes. Their formulas and measurements were suspiciously similar.

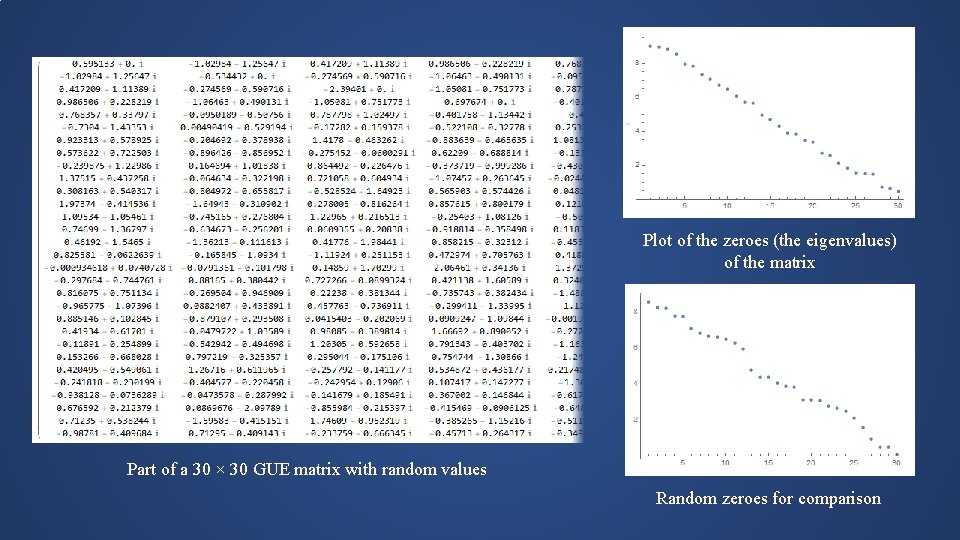
Plot of the zeroes (the eigenvalues) of the matrix Part of a 30 × 30 GUE matrix with random values Random zeroes for comparison

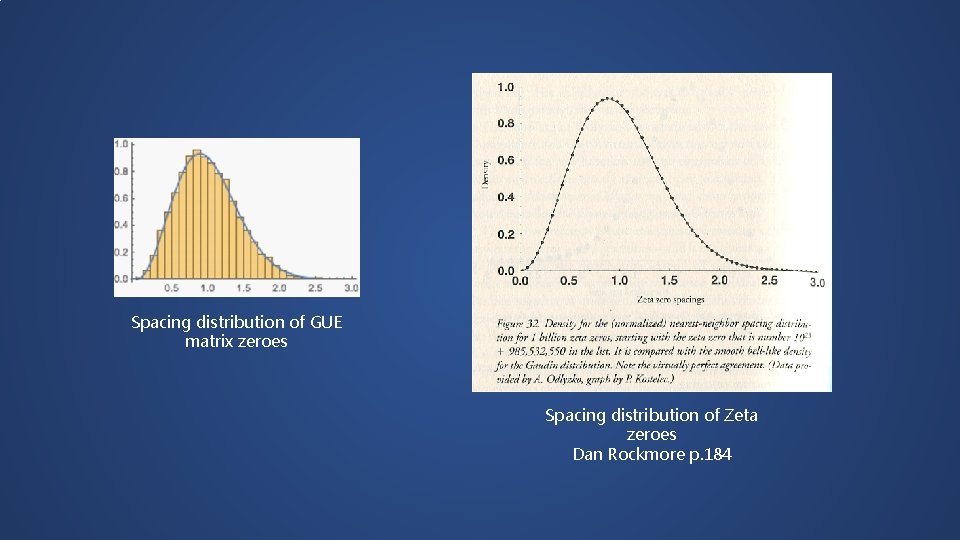
Spacing distribution of GUE matrix zeroes Spacing distribution of Zeta zeroes Dan Rockmore p. 184

Pair correlation of random values Dan Rockmore p. 222 Pair correlation of Zeta zeroes Dan Rockmore p. 159 The solid line is the expected pair correlation for GUE matrix zeroes. Energy levels in the spectrum of heavy elements have the same ‘repulsive’ effect as the GUE and Zeta zeroes.

John Derbyshire Prime Obsession p. 295

The Evidence The Judgement

Some famous names believe it is outright false: Littlewood, Turing, Ivić. Other functions in the ‘zeta family’ satisfy a similar hypothesis. Some famous names believe there is some reasonable doubt: Bombieri, Sarnak, Conrey. Results of Artin and Weil, and Deligne’s 1973 proof of the Weil Conjectures. Numerical evidence is inadmissible due to so many failed historical hunches. Some believe that failures will happen far beyond our current reach. Even Riemann said it was “very likely”, but many of the reasons for him to say that have been disproved since 1859. The density of zeroes is slowly increasing towards 1 (currently at 2/5). The similar behaviour to zeroes of a GUE matrix. Denjoy’s probabilistic argument (odd/even number of distinct divisors of a random number is like a coin toss). Truth would suggest that “the primes are distributed as regularly as possible”.

The Verdict It’s hopeless… I’m going down the pub. Who’ll join me? Trial Postponed We end on the sad note that a verdict on the Riemann hypothesis is currently impossible. The judge can’t be found, the witnesses are contradicting each other and a lot of the evidence is incomprehensible. Solve any Millennium Prize Problem stated by the Clay Mathematics Institute in May 2000 and win a million dollars.

The Clay Mathematics Institute in May 2000 offered a $1, 000 dollar prize for a verdict on the Riemann hypothesis.