The Gibbs Free Energy Function and Phase Transitions

The Gibbs Free Energy Function and Phase Transitions H 2 O(l) --> H 2 O(s) Normal freezing point of H 2 O = 273. 15 K The change in enthalpy is the enthalpy of freezing - enthalpy change associated when one mole of liquid water freezes at 1 atm and 273. 15 K DH = -6007 J Entropy change DH -6007 J = = -21. 99 J/K DS= T 273. 15 K DG = DH - TDS = -6007 J - (273. 15 K)(-21. 99 J/K) = 0 J => at 273. 15 K and 1 atm, liquid and solid water are at equilibrium

As water is cooled by 10 K below 273. 15 K to 263. 15 K Assume that DH and DS do not change with T DG = DH - TDS = -6007 J - (263. 15 K)(-21. 99 J/K) = -220 J Since DG < 0 water spontaneously freezes At 10 K above the freezing point, 283. 15 K DG = DH - TDS = -6007 J - (283. 15 K)(-21. 99 J/K) = 219 J DG > 0 water does not spontaneously freeze at 283. 15 K, 10 K above the normal freezing point of water Above 273. 15 K, the reverse process is spontaneous - ice melts to liquid water.

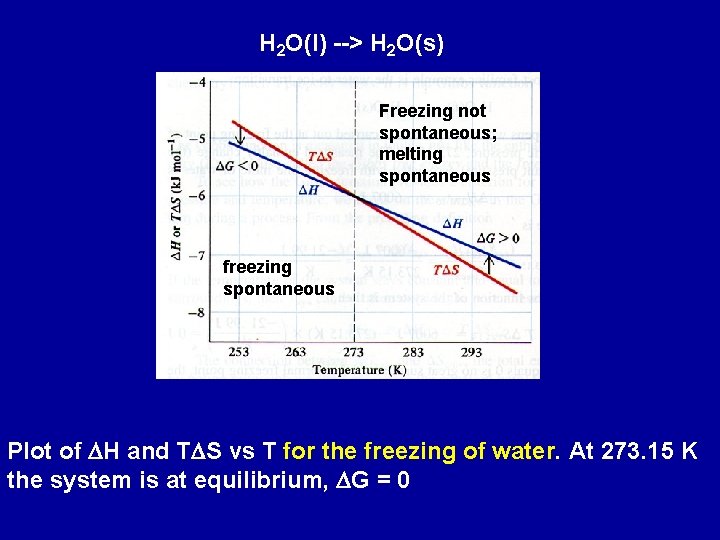
H 2 O(l) --> H 2 O(s) Freezing not spontaneous; melting spontaneous freezing spontaneous Plot of DH and TDS vs T for the freezing of water. At 273. 15 K the system is at equilibrium, DG = 0

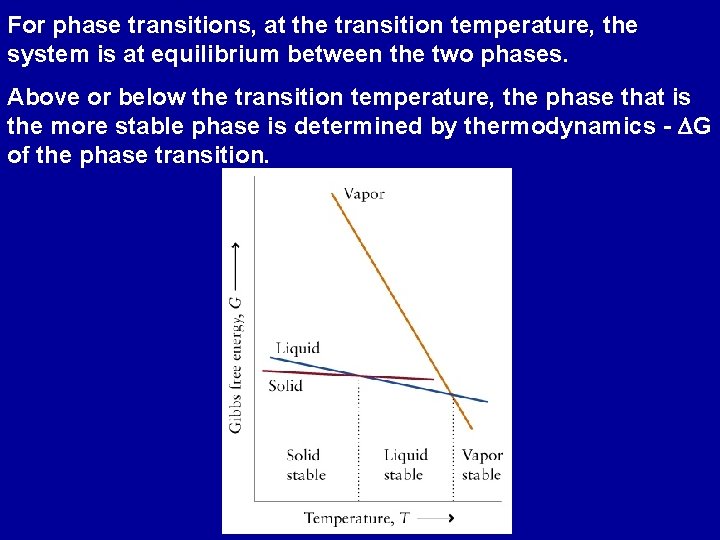
For phase transitions, at the transition temperature, the system is at equilibrium between the two phases. Above or below the transition temperature, the phase that is the more stable phase is determined by thermodynamics - DG of the phase transition.

Reaction Free Energy DGr = Sn. Gm(products) - Sn. Gm(reactants) Standard Reaction Free Energy DGor = Sn. Gom (products) - Sn. Gom(reactants) Difference in free energy of the pure products in their standard states and pure reactants in their standard states.

Standard Free-Energy of Formation The standard free energy of formation, DGfo, of a substance is the standard reaction free energy per mole for the formation of a compound from its elements in their most stable form 1/2 N 2 (g) + 3/2 H 2 (g) --> NH 3(g) DGfo = -16 k. J O 2 (g) --> O 2 (g) DGfo = 0

DGfo is an indication of a compounds stability relative to its elements Thermodynamically stable compound DGfo < 0 Thermodynamically unstable compound DGfo > 0

Standard Reaction Free Energy For a reaction: a. A + b. B --> c. C + d. D DGro = c DGfo (C) + d DGfo(D) - a DGfo(A) -b DGfo(B) The standard free energy of formation of elements in their most stable form at 298. 15 K is zero.

Problem: Calculate the standard free-energy change for the following reaction at 298 K: N 2(g) + 3 H 2 (g) --> 2 NH 3(g) Given that DGfo[NH 3(g)] = -16. 66 k. J/mol. What is the DGo for the reverse reaction? Since the reactants N 2(g) and H 2(g) are in their standard state at 298 K their standard free energies of formation are defined to be zero. DGro = 2 DGfo[NH 3(g)] - DGfo[N 2(g)] - 3 DGfo[H 2(g)] = 2 x -16. 66 = -33. 32 k. J/mol For the reverse reaction: 2 NH 3(g) --> N 2(g) + 3 H 2 (g) DGro = +33. 32 k. J/mol

C 3 H 8(g) + 5 O 2(g) --> 3 CO 2 (g) + 4 H 2 O(l) DHo = - 2220 k. J a) Without using the information from the tables of thermodynamic quantities predict whether DGo for this reaction will be less negative or more negative than DHo. b) Use data from App. D to calculate DGro for this reaction. Whether DGro is more negative or less negative than DHo depends on the sign of DSo since DGro = DHo - T DSo The reaction involves 6 moles of gaseous reactants and produces 3 moles of gaseous product => DSo < 0 (since fewer moles of gaseous products than reactants) Since DSo < 0 and DHo < 0 and DGro = DHo - T DSo => DGro is less negative than DHo

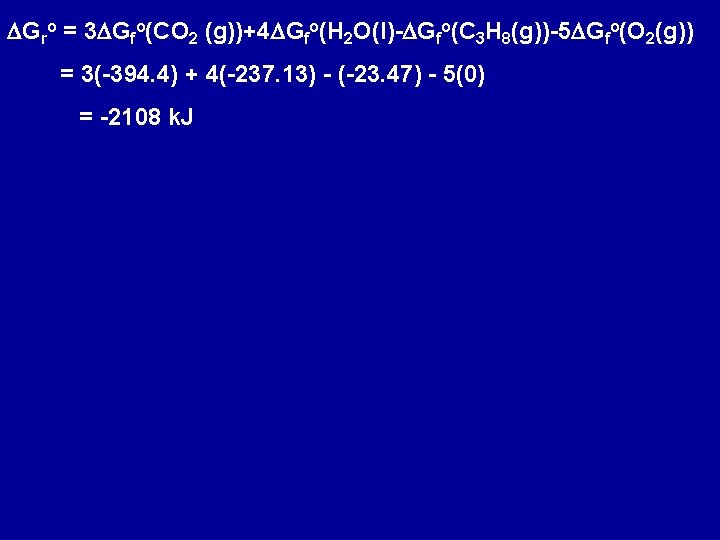
DGro = 3 DGfo(CO 2 (g))+4 DGfo(H 2 O(l)-DGfo(C 3 H 8(g))-5 DGfo(O 2(g)) = 3(-394. 4) + 4(-237. 13) - (-23. 47) - 5(0) = -2108 k. J

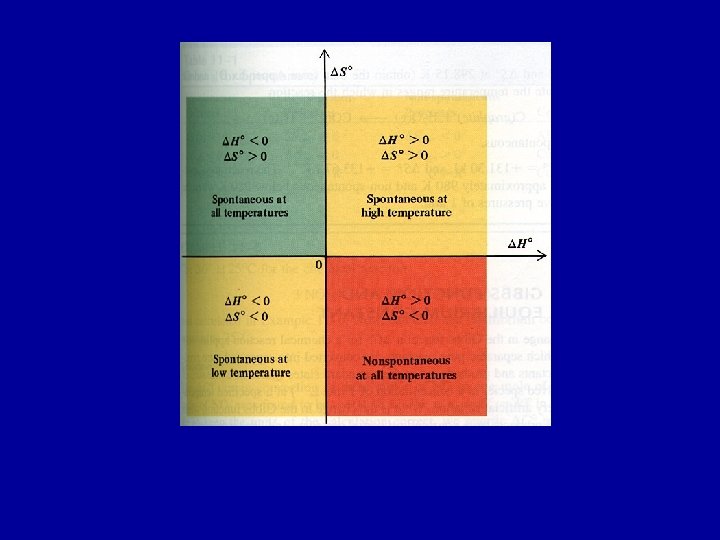
Effect of temperature on DGo Values of DGro calculated using the tabulated values of DGfo apply only at 298. 15 K. For other temperatures the relation: DGro = DHo - T DSo can be used, assuming DHo and DSo do not vary significantly with temperature. When DGr = 0, T = o DHo DSo Use this expression to determine temperature above or below which reaction becomes spontaneous.

Problem: The normal boiling point is the temperature at which a pure liquid is in equilibrium with its vapor at 1 atm. a) write the chemical equation that defines the normal boiling point of liquid CCl 4 b) what is the value of DGo at equilibrium? c) Use thermodynamic data to estimate the boiling point of CCl 4. a) CCl 4(l) CCl 4(g) b) At equilibrium DG = 0. In any equilibrium for a normal boiling point, both the liquid and gas are in their standard states. Hence, for this process DG is DGo.

c) o DH T= DSo where for this reaction T is the boiling point Note: To determine the boiling point accurately we need the values of DHo and DSo for the vaporization process at the boiling point of CCl 4 DHo = (1 mol)(-106. 7 k. J/mol) - (1 mol)(-139. 3 k. J/mol) = 32. 6 k. J DSo = (1 mol)(309. 4 J/mol-K) -(1 mol)(214. 4 J/mol-K) = 95. 0 J/K o DH T= DSo = 32. 6 k. J 0. 095 k. J/K = 343 K

The Gibbs Function and the Equilibrium Constant DG = DGro + R T ln Q Q - reaction quotient Under standard conditions the concentrations of all reactants and products are set to 1 (standard pressure of gases = 1 atm Standard pressure of solutions = 1 M) Under standard conditions, ln Q = 0 => DG = DGro

At equilibrium DG = 0 and Q = K At equilibrium DGro = - R T ln K or K = e- DGr o /RT DGro < 0 => K > 1 DGro > 0 => K < 1 DG = DGro + R T ln Q = - RT ln K + RT ln Q DG = R T ln Q K when Q = K => DG = 0; equilibrium

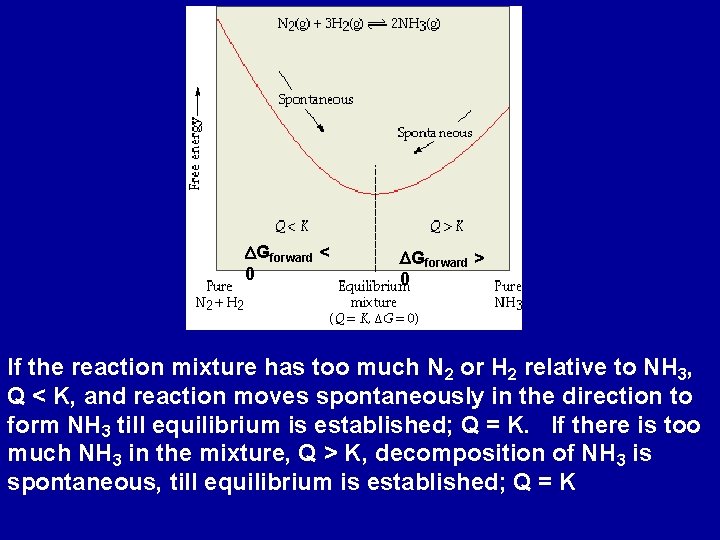
DGforward < 0 DGforward > 0 If the reaction mixture has too much N 2 or H 2 relative to NH 3, Q < K, and reaction moves spontaneously in the direction to form NH 3 till equilibrium is established; Q = K. If there is too much NH 3 in the mixture, Q > K, decomposition of NH 3 is spontaneous, till equilibrium is established; Q = K

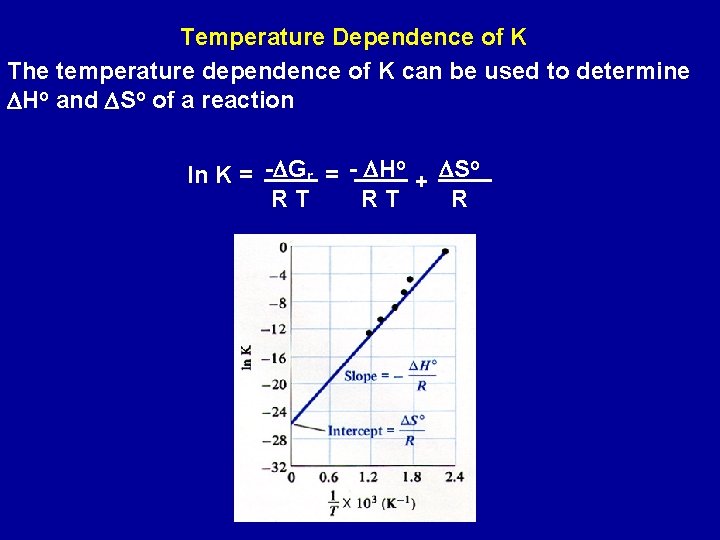
Temperature Dependence of K The temperature dependence of K can be used to determine DHo and DSo of a reaction o o ln K = -DGr = - DH + DS RT RT R

If the equilibrium constant of a reaction is known at one temperature and the value of DHo is known, then the equilibrium constant at another temperature can be calculated o o DH DS ln K 1 = + R T 1 R o o ln K 2 = - DH + DS R T 2 R ln K 2 - ln K 1 = ln K 2 = K 1 DHo R ( 1 - 1 T 2 ) If DHo is negative (exothermic), an increase in T reduces K; if it is positive (endothermic), an increase in T increases K

For the equilibrium between a pure liquid and its vapor, the equilibrium constant is simply the equilibrium vapor pressure (since pure liquids do not appear in the equilibrium expression) Liquid Gas K = Pgas Hence ln p 2 = DHvap ( 1 - 1 p 1 R T 1 T 2 ) Clausius-Clapeyron equation The Clausius-Clapeyron equation indicates the variation of vapor pressure of a liquid with temperature

Driving Non-spontaneous Reactions The magnitude of DG is a useful tool for evaluating reactions. For a spontaneous process at constant pressure and temperature, the change in free energy for a process equals the maximum amount of work that can be done by the system on its surroundings wmax = DGr For non-spontaneous reactions (DGr > 0), the magnitude of DGr is a measure of the minimum amount of work that must be done on the system to cause the process to occur. A reaction for which DGr is large and negative (like the combustion of gasoline), is much more capable of doing work on the surroundings than a reaction for which DGr is small and negative (like the melting of ice).

Many chemical reactions, including a large number that are central to biological systems, are non-spontaneous. For example: Cu can be extracted from the mineral chalcolite which contains Cu 2 S. The decomposition of Cu 2 S is non-spontaneous Cu 2 S --> 2 Cu(s) + S(s) DGro = +86. 2 k. J Since this reaction is not spontaneous Cu cannot be directly obtained from the above reaction. Instead, work needs to be done on this reaction, and this is done by coupling this non-spontaneous reaction with a spontaneous reaction so that the overall reaction is spontaneous.

Consider the following reaction: S(s) + O 2(g) --> SO 2 (g) DGro = -300. 4 k. J Coupling this reaction with the extraction of Cu from Cu 2 S Net: Cu 2 S --> 2 Cu(s) + S(s) DGro = +86. 2 k. J S(s) + O 2(g) --> SO 2 (g) DGro = -300. 4 k. J Cu 2 S(s) + O 2 (g) --> 2 Cu(s) + SO 2(g) DGro = -214. 2 k. J

Biological systems employ the same principle by using spontaneous reactions to drive non-spontaneous reactions. Many biochemical reactions are not spontaneous. These reactions are made to occur by coupling them with spontaneous reactions which release heat. The metabolism of food is the usual source of free energy needed to do the work to maintain biological systems. C 6 H 12 O 6(s) + 6 O 2 (g) --> 6 CO 2 (g) + 6 H 2 O(l) DHo = -2803 k. J

A means of transporting the energy released by glucose metabolism to the reactions that require energy is needed. The free energy released by the metabolism of glucose is used to convert lower-energy ADP (adenine diphosphate) to higher energy ATP (adenine triphosphate). The energy stored in the ATP molecule is then available to a biochemical reaction that requires energy and in the process ATP is converted to ADP.

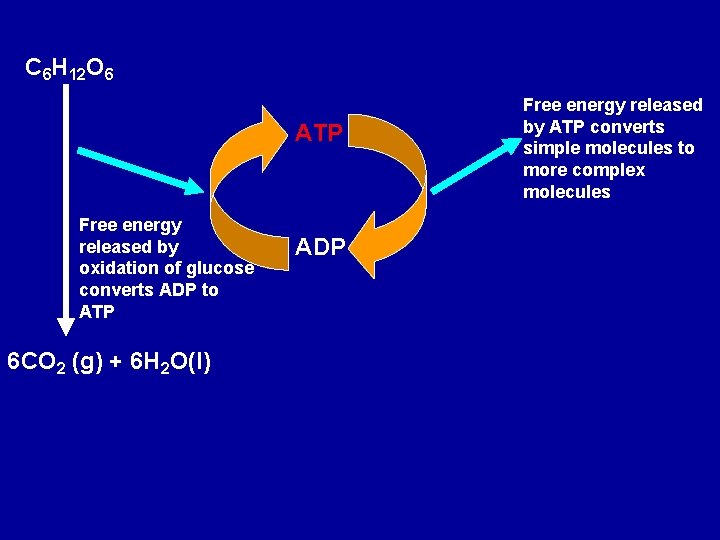
C 6 H 12 O 6 ATP Free energy released by oxidation of glucose converts ADP to ATP 6 CO 2 (g) + 6 H 2 O(l) ADP Free energy released by ATP converts simple molecules to more complex molecules