The gerade Rydberg states of molecular hydrogen Daniel

The gerade Rydberg states of molecular hydrogen Daniel Sprecher, 1 Christian Jungen, 2 and Frédéric Merkt 1 1 2 Laboratory of Physical Chemistry, ETH Zurich, Switzerland Laboratoire Aimé Cotton du CNRS, Campus d‘Orsay, France International Symposium on Molecular Spectroscopy Ohio State University, June 20 -24, 2011 TH 07, June 21, 3: 45 pm, 1000 Mc. Pherson Lab

Motivation • Measurement of rotational, vibrational, spin-rotation, and hyperfine splittings of H 2+: Ø Test of ab initio calculations in one-electron systems Ø Metrology of fundamental constants (proton-to-electron mass ratio) • Problem: essentially no electric dipole spectrum • Solution: spectroscopy of high-n Rydberg states of H 2 • Requirement: model to extrapolate Rydberg series • Expected perturbations: Ø Ø Ø rotational, vibrational and electronic channel interactions s-d and p-f mixing fine and hyperfine splittings singlet-triplet mixing and other uncoupling phenomena shifts from the interaction with dissociation continua role of nuclear spin in photoionization

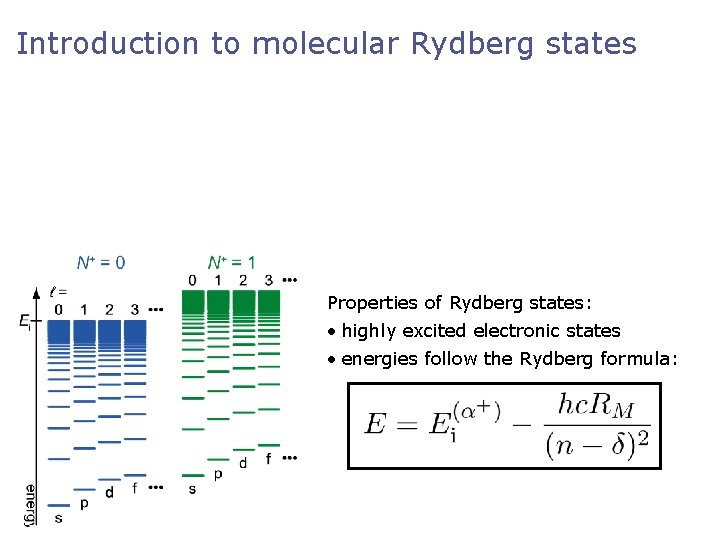
Introduction to molecular Rydberg states Properties of Rydberg states: • highly excited electronic states • energies follow the Rydberg formula:

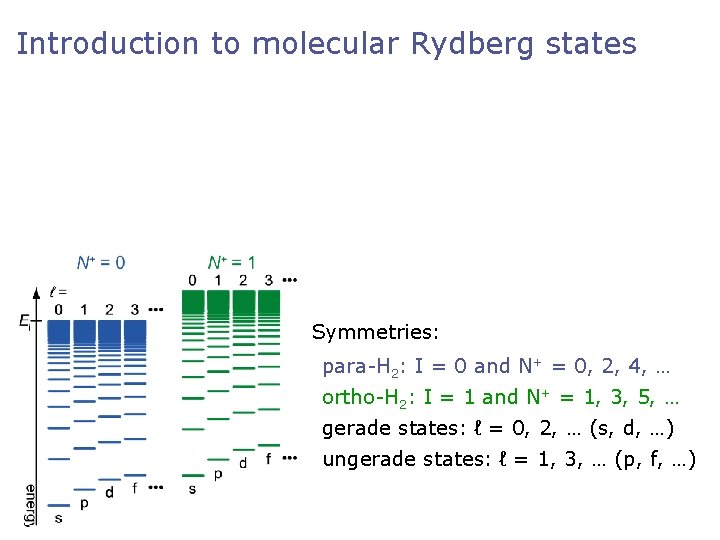
Introduction to molecular Rydberg states Symmetries: para-H 2: I = 0 and N+ = 0, 2, 4, … ortho-H 2: I = 1 and N+ = 1, 3, 5, … gerade states: ℓ = 0, 2, … (s, d, …) ungerade states: ℓ = 1, 3, … (p, f, …)

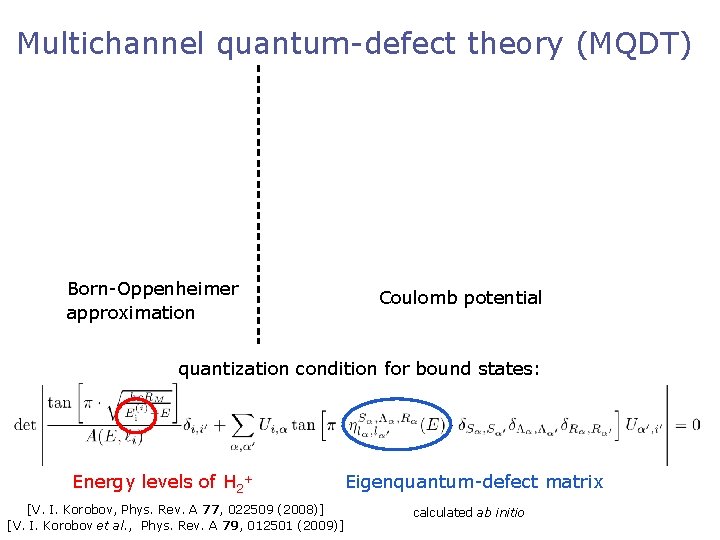
Multichannel quantum-defect theory (MQDT) Born-Oppenheimer approximation Coulomb potential quantization condition for bound states: Energy levels of H 2+ [V. I. Korobov, Phys. Rev. A 77, 022509 (2008)] [V. I. Korobov et al. , Phys. Rev. A 79, 012501 (2009)] Eigenquantum-defect matrix calculated ab initio

The eigenquantum-defect functions ungerade manifold p 1Σ s 1Σ d 1Σ sd 1Σ d 1Δ d 1Π all f p 1Π H 2+ 2 pσ (2 pσ)2 H 2+ 1 sσ 4 pσB”B 4 dσP 3 pσB' 3 dσGK 2 pσB 2 sσEF

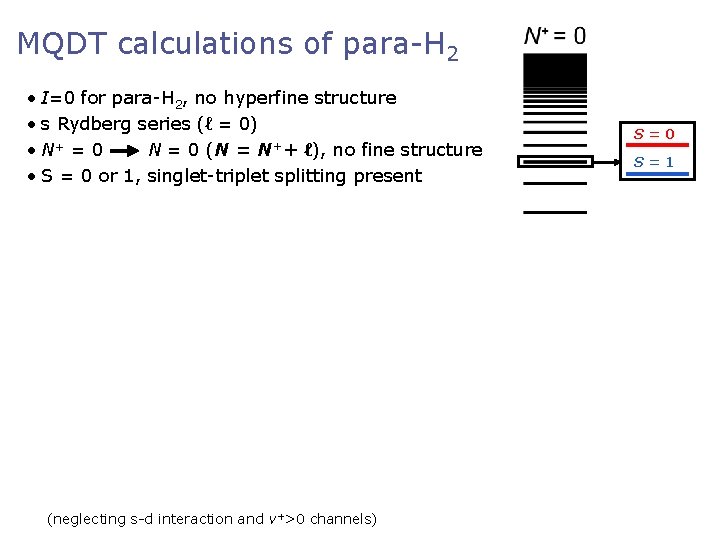
MQDT calculations of para-H 2 • I=0 for para-H 2, no hyperfine structure • s Rydberg series (ℓ = 0) • N+ = 0 N = 0 (N = N++ ℓ), no fine structure • S = 0 or 1, singlet-triplet splitting present (neglecting s-d interaction and v+>0 channels) S=0 S=1

MQDT calculations of para-H 2 • p Rydberg series (ℓ = 1), S = 0 • N+ = 0 N = 1 (N = N++ ℓ), no fine structure rotational channel interaction • N+ = 2 N = 3, 2, 1 p, ℓ = 1, N = 1 d, ℓ = 2, N = 2 N+ = 0 f, ℓ = 3, N = 3

MQDT calculations of para-H 2 • s Rydberg series (ℓ = 0) • N+ = 0 N = 0, no fine structure • N+ = 2 only N = 2 for ℓ = 0, but N = 4, 3, 2, 1, 0 for ℓ = 2 neglect s-d interaction neglect v+>0 channels S=1 S=0 include s-d interaction neglect v+>0 channels include s-d interaction include v+=1 channels

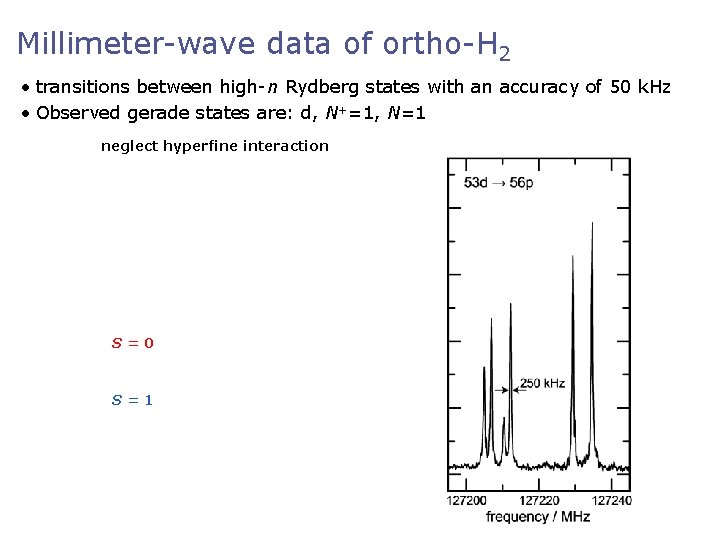
Millimeter-wave data of ortho-H 2 • transitions between high-n Rydberg states with an accuracy of 50 k. Hz • Observed gerade states are: d, N+=1, N=1 neglect hyperfine interaction include hyperfine interaction G+=1/2 S=0 S=1 G+=3/2

Millimeter-wave data of ortho-H 2 • For the G+=3/2 hyperfine components: observed ab initio MQDT calculation

The gerade d (N=1) Rydberg series G+=3/2 G+=1/2 rms deviation: 400 k. Hz G+=3/2

Laser spectra of the d Rydberg series [H. J. Wörner, Ph. D thesis (2007)]

Laser spectra of the d Rydberg series N=1 N=3 N=2 [H. J. Wörner, Ph. D thesis (2007)]

Laser spectra of the d Rydberg series N=1 N=3 N=2 n=18, N+=3

Laser spectra of the d Rydberg series N=1

Laser spectra of the d Rydberg series n=7, ℓ=0, S=1, N+=1, v+=1 N=1

Conclusions • Multichannel quantum-defect theory can reproduce the energies of high-n Rydberg states with an accuracy of better than 1 MHz Energy levels of H 2+ spectroscopy of H 2+ Eigenquantum-defect matrix