The Geometry of a Tetrahedron Footnote 18 Section

The Geometry of a Tetrahedron Footnote 18: Section 10. 4 Mark Jeng Professor Brewer

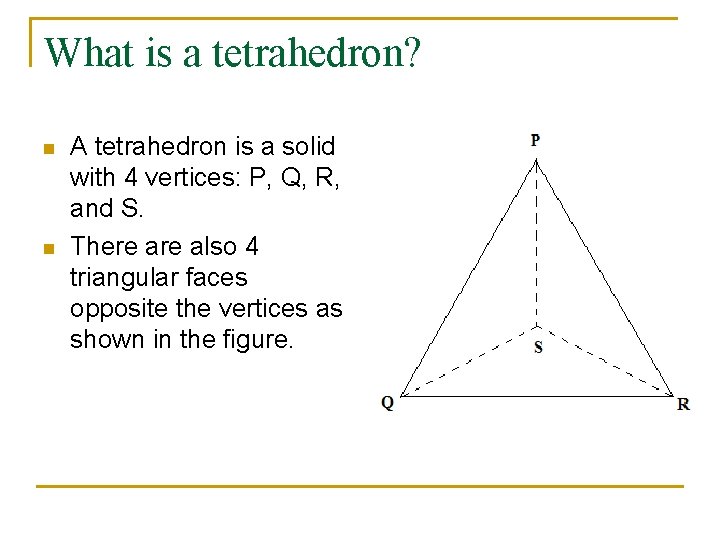
What is a tetrahedron? n n A tetrahedron is a solid with 4 vertices: P, Q, R, and S. There also 4 triangular faces opposite the vertices as shown in the figure.

Problem 1 1. Let v 1, v 2, v 3, and v 4 be vectors with lengths equal to the areas of the face opposite the vertices P, Q, R, and S, respectively, and direction perpendicular to the respective faces and pointing outward. Show that: v 1 + v 2 + v 3 + v 4 = 0

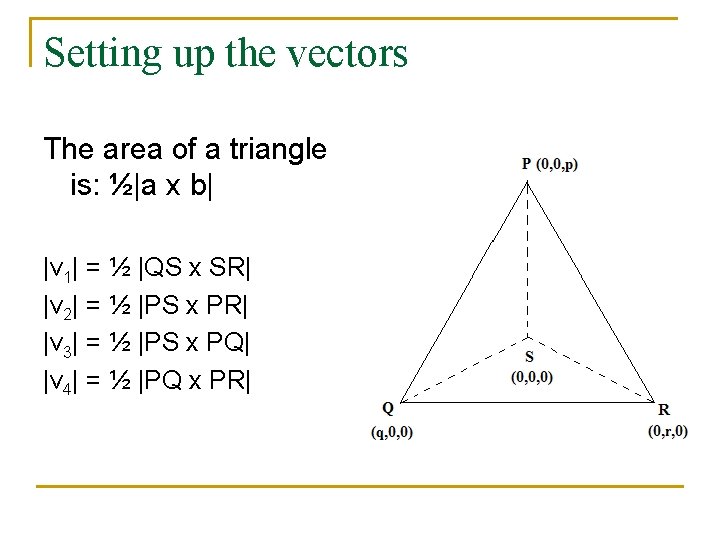
Setting up the vectors The area of a triangle is: ½|a x b| |v 1| = ½ |QS x SR| |v 2| = ½ |PS x PR| |v 3| = ½ |PS x PQ| |v 4| = ½ |PQ x PR|

Vector 1 |v 1| = ½ |i(0) – j(0) + k(-qr)| = ½ |<0, 0, -qr>| = ½ qr The direction of the vector is pointing outward from the xy-axis, so therefore the final vector is: v 1 = <0, 0, -½ qr>

Vector 2 |v 2| = ½ |i(pr) – j(0) + k(0)| = ½ |<pr, 0, 0>| = ½ pr The direction of the vector is pointing outward from the yz-axis, so therefore the final vector is: v 2 = <-½ pr , 0, 0>

Vector 3 |v 3| = ½ |i(0) – j(pq) + k(0)| = ½ |<0, -pq, 0>| = ½ pq The direction of the vector is pointing outward from the xz-axis, so therefore the final vector is: v 3 = <0, -½ pq, 0>

Vector 4 |v 4| = ½ |i(-pr) – j(-pq) + k(qr)| = ½ |<-pr, pq, qr>| = ½ √[(-pr)2 + (pq)2 + (qr)2] The vector is pointing outward in the +x, +y, and +z directions perpendicular to the plane PQR; therefore the final vector is: v 4 = <½ pr, ½ pq, ½ qr>

Question 1 Results Show that: v 1 + v 2 + v 3 + v 4 = 0 <0, 0, -½ qr> + <-½ pr , 0, 0> + <0, -½ pq, 0> + <½ pr, ½ pq, ½ qr> = 0 The x, y, and z components of the vectors all cancel out

Problem 2 2. The volume V of a tetrahedron is 1/3 the distance from a vertex to the opposite face, times the area of that face. (a) Find a formula for the volume of a tetrahedron in terms of the coordinates of its vertices P, Q, R, and S. (b) Find the volume of the tetrahedron whose vertices are P(1, 1, 1), Q(1, 2, 3), R(1, 1, 2), and S(3, -1, 2).

Formula for Tetrahedron Volume (a) The volume of a tetrahedron is: V = 1/3 d[(s 1, s 2, s 3), Plane. PQR] * ½ |PQ x PR| where (s 1, s 2, s 3) are the x, y, and z components of point S, the vertex opposite Plane. PQR

Finding the Volume (b) Find the volume using the formula: V = 1/3 d[(s 1, s 2, s 3), Plane. PQR] * ½ |PQ x PR| with points P(1, 1, 1), Q(1, 2, 3), R(1, 1, 2), and S(3, -1, 2). The first step is to derive the vectors PQ and PR: v. PQ = <1 -1, 2 -1, 3 -1> = <0, 1, 2> v. PR = <1 -1, 2 -1> = <0, 0, 1>

Finding the Volume (cont. ) Using those 2 vectors, find the Area of that face: ½ |PQ x PR| = ½ |i(1) – j(0) – k(0)| ½ = ½ |<1, 0, 0>| = ½ √(12 + 02) =½

Finding the Volume (cont. ) Then, using those same 2 vectors and point P(1, 1, 1), find the equation of the Plane. PQR. In the previous slide, the cross product of those 2 vectors was determined: <1, 0, 0> The general equation of a plane is: A(x-x 0) + B(y-y 0) + C(z-z 0) = 0 where <A, B, C> is <1, 0, 0> and <x 0, y 0, z 0> is <1, 1, 1> The equation of Plane. PQR is then: 1(x-1) = 0

Finding the Volume (cont. ) The formula for the distance between a point and a plane is: D = |Ax 1 + By 1 + Cz 1 + D| / √(A 2 + B 2 + C 2) Using the equation of the plane, x-1 = 0, and the point S(3, -1, 2), the distance will be: D = |1(3) + 0(-1) + 0(2) + (-1)| / √(1 + 0) =2

Finding the Volume (cont. ) Now, going back to the volume of a tetrahedron formula: V = 1/3 d[(s 1, s 2, s 3), Plane. PQR] * ½ |PQ x PR| Plug in all the components V = 1/3*(2)*(1/2) = 1/3

Problem 3 3. Suppose the tetrahedron in the figure has a tri-rectangular vertex S. (This means that the 3 angles at S are all right angles. ) Let A, B, and C be the areas of the 3 faces that meet at S, and let D be the area of the opposite face PQR. Using the result of Problem 1, show that: D 2 = A 2 + B 2 + C 2

3 -D Pythagorean Theorem Going back to the results of Problem 1, the areas of the faces are: A = ½ qr B = ½ pr C = ½ pq D = ½ √[(-pr)2 + (pq)2 + (qr)2]

3 -D Pythagorean Theorem (cont. ) Therefore, D 2 = A 2 + B 2 + C 2: (½ √[(-pr)2 + (pq)2 + (qr)2])2 = (½ qr)2 + (½ pq)2 ¼[(pr)2 + (pq)2 + (qr)2] = ¼ (qr)2 + ¼ (pr)2 + (pq)2 The 3 -D Pythagorean Theorem is verified