The Generalized BrainStateinaBox g BSB Neural Network Model

The Generalized Brain-State-in-a-Box (g. BSB) Neural Network: Model, Analysis, and Applications Cheolhwan Oh---Purdue Stefen Hui---SDSU Stanisław H. Żak---Purdue October 18, 2005 1

Outline n n n Modeling q Linear associative memory q Brain-State-in-a-Box (BSB) neural net q The generalized BSB (g. BSB) Analysis q Stability defintions q Stability tests Applications q Associative memory design using g. BSB net q Large scale g. BSB nets q Storing and retrieving images 2

Neural Associative Memory n Associative memory: a memory that can be accessed by contents---Content Addressable Memory (CAM) n Autoassociative memory: stored patterns are retrieved from their distorted versions 3

Neural Associative Memory (continued) n Heteroassociative memory: a set of input patterns is paired with a different set of output patterns n Two stages of neural associative memory operation: Storage phase: Patterns are stored by the neural network Recall phase: Memorized patterns are retrieved in response to given initial patterns 4

Linear Associative Memory (LAM) n n v(1), …, v(r) are mutually orthogonal pattern vectors LAM recovers stored pattern from the partial input Let Then 5

Limitations of Linear Associative Memory (LAM) q q Patterns must be orthogonal to each other When the input vector is a noisy version of the prototype pattern, the LAM cannot recall the corresponding prototype pattern 6

Brain-State-in-a-Box (BSB) neural network n BSB model---a nonlinear dynamical system n Proposed by Anderson, Silverstein, Ritz and Jones (1977) as a memory model based on neurophysiological considerations n Used to model effects and mechanisms seen in psychology and cognitive science 7

Brain-State-in-a-Box (BSB) neural network (continued) n Can be used to recognize a pattern from its given noisy version n The network trajectory is constrained to be in the hypercube Hn = [– 1, 1]n 8

Dynamics of the BSB neural model x(k+1) = g(x(k) + αWx(k)), x(0)=x 0 x 0: initial condition x(k) ∈ ℝn: state of the BSB net at time k α ∈ ℝ: step size W ∈ ℝn×n: symmetric weight matrix g: ℝn → ℝn: activation function (standard linear saturation function) 9

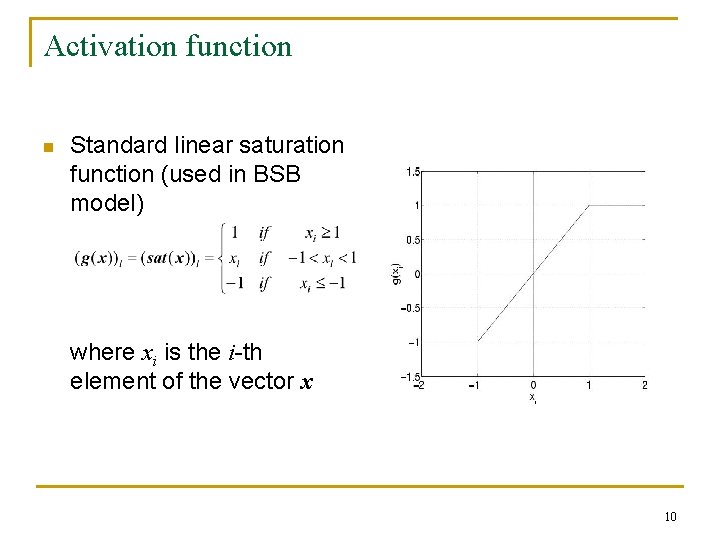
Activation function n Standard linear saturation function (used in BSB model) where xi is the i-th element of the vector x 10

Super stable equilibrium state n Equilibrium state: A point xe is an equilibrium state of the dynamical system x(k+1) = T(x(k)) if xe = T(xe) n Super stable equilibrium state: An equilibrium state xe is super stable if there exists a neighborhood of xe, denoted N(xe), such that for any initial state x 0 ∈ N(xe), the trajectory starting from x 0 reaches xe in a finite number of steps 11

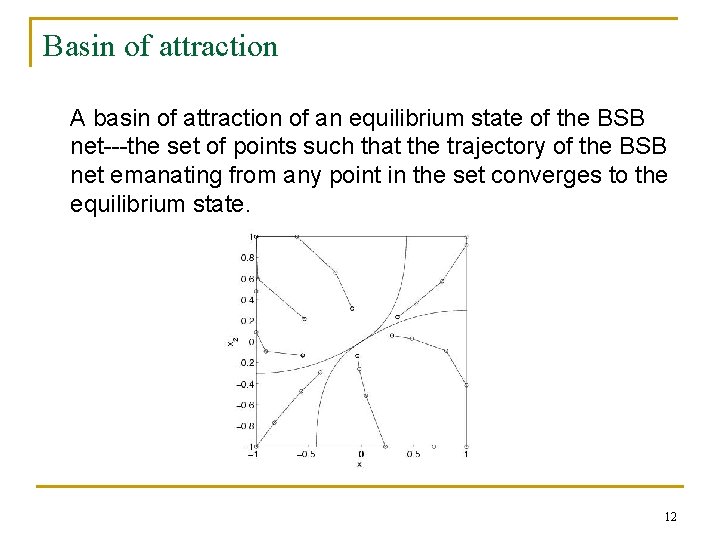
Basin of attraction A basin of attraction of an equilibrium state of the BSB net---the set of points such that the trajectory of the BSB net emanating from any point in the set converges to the equilibrium state. 12

Characteristics of BSB based neural associative memories n n n If an equilibrium state is a vertex of the hypercube Hn = [– 1, 1]n, then belongs to the set {– 1, 1}n Pattern vectors are stored as super stable equilibrium vertices If an initial state (noisy pattern) is located in the basin of attraction of a certain stored pattern, the network trajectory starting from the given initial state converges to this pattern---we say that recall is successful 13

Generalized Brain-State-in-a-Box (g. BSB) neural network n n n Proposed by Hui and Żak (1992) Weight matrix can be nonsymmetric → easier to implement Offers more control of the volume of the basin of attraction of an equilibrium state 14

Dynamics of g. BSB model x(k+1) = g((In + αW)x(k) + αb), x(0)=x 0 W ∈ ℝn×n: weight matrix (not necessarily symmetric) b ∈ ℝn: bias vector In ∈ ℝn: identity matrix g: ℝn → ℝn: standard linear saturation function 15

Stability condition for g. BSB neural model n n Let v = [v 1 v 2 ··· vn]T ∈ {– 1, 1}n (v is a vertex of Hn) v is an equilibrium state of the g. BSB model if and only if (Wv + b)i vi ≥ 0 for i=1, …, n v is a super stable equilibrium state of the g. BSB model if (Wv + b)i vi > 0 for i=1, …, n The above stability conditions are also called the vertex stability conditions 16

Synthesis of g. BSB neural associative memory n Weight matrix construction algorithm of Lillo, Miller, Hui and Żak (1994) n Given pattern vectors to be stored: v(j) ∈ {– 1, 1}n, j=1, 2, …, r Form a matrix B = [b b ··· b]T ∈ ℝn×r, where n 17

Synthesis of g. BSB neural associative memories (continued) n Choose D ∈ ℝn×n such that n Choose ∈ ℝn×n such that 18

Synthesis of g. BSB neural associative memories (continued) n Determine the weight matrix W , W = (DV – B)V† + (In – VV†), where V = [v(1) v(2) ··· v(r)] ∈ {– 1, 1}n×r and V† is a pseudo-inverse matrix of V n The above implementation procedure guarantees that the given patterns are stored as super stable vertices of Hn 19

Simulation experiments n Prototype patterns n Stacking operator 20

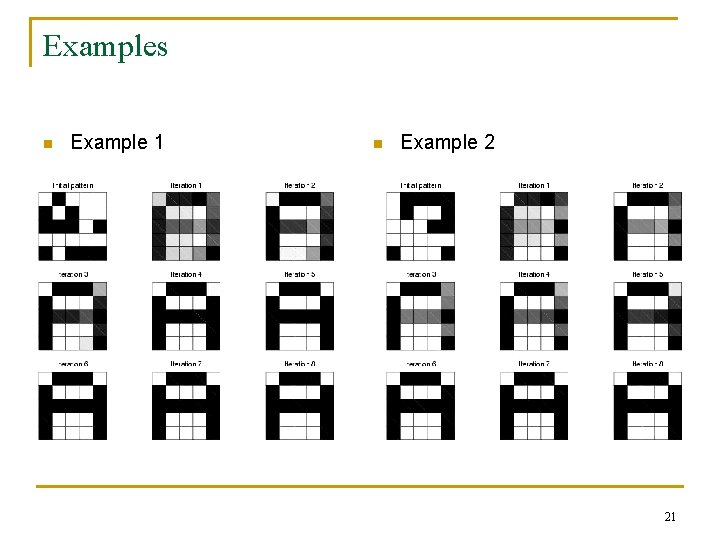
Examples n Example 1 n Example 2 21

Large scale neural associative memory design n n Neural associative memory: a memory that can be accessed by content and is constructed using an artificial neural network Difficulty with neural associative memory design: quadratic growth of the number of interconnections with the problem size Large scale patterns → Large scale neural network → Heavy computational overhead Proposed approach---apply pattern decomposition 22

Large scale neural associative memory design using pattern decomposition n n Advantages: Computationally efficient (Smaller size of weight matrices) Disadvantages of pattern decomposition: Small size patterns → Small size neural networks → Deterioration of recall performance---reduced capacity, more spurious states 23

Associative memory design using overlapping pattern decomposition n Purpose q Take the advantage of decomposed neural associative memory q Enhance recall performance n Design Each neural subnetwork is constructed independently of other subnetworks 24

Ring overlapping pattern decomposition n Disjoint decomposition v 1 n v 2 k+1 vpk Overlapping decomposition v 1 n vk vk+1 v 2 k vpk Overlapping decomposition with a ring structure v 1 vk vk+1 v 2 k vpk v 1 25

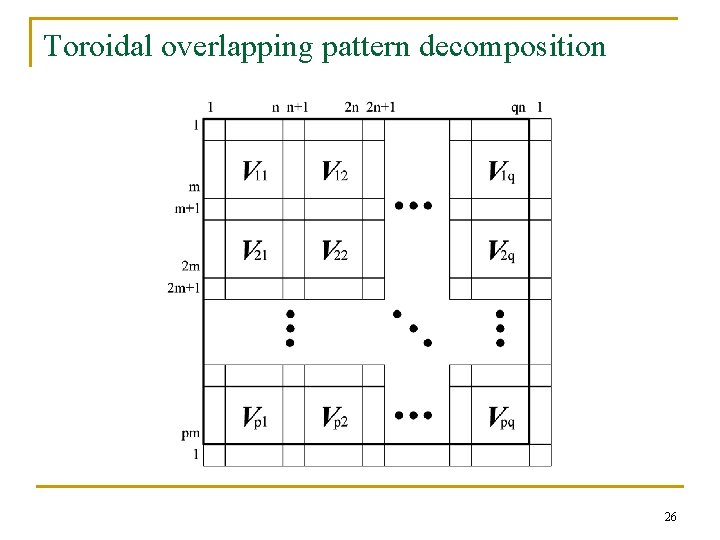
Toroidal overlapping pattern decomposition 26

Proposed associative memory system n Storage phase q q Decompose prototype patterns into subpatterns with overlapping pattern decomposition structure Construct subnetworks independently of each other 27

Proposed associative memory system (continued) n Recall phase q q Initial pattern decomposed into subpatterns Subnetworks process corresponding initial subpatterns (retrieval processes) Check the overlapping portions and apply error correction procedure Recombine the output subpatterns 28

Error correction for vector patterns n Input subpatterns Output subpatterns of the retrieval processes 29

Error correction for vector patterns (continued) n Check if there are mismatches in the overlapping portions between neighboring subpatterns, i. e. , n If , recall error occurred Error correction algorithm q Form a modified input subpattern and go through retrieval process again with the modified input subpattern n 30

Error correction for matrix patterns n n Direct extension of the error correction procedure for the vector patterns Replace overlapping rows or overlapping columns of a matrix with the corresponding rows or columns of neighboring subpatterns 31

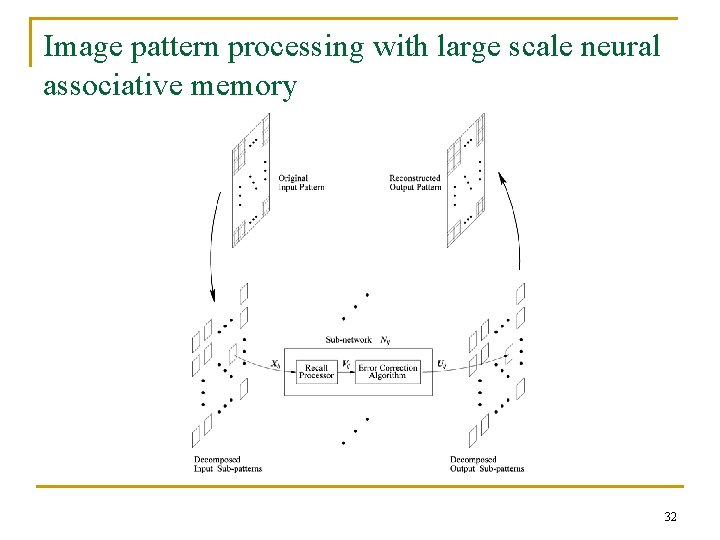
Image pattern processing with large scale neural associative memory 32

Black and white image patterns Pattern size: 200 -by-200 pixel 33

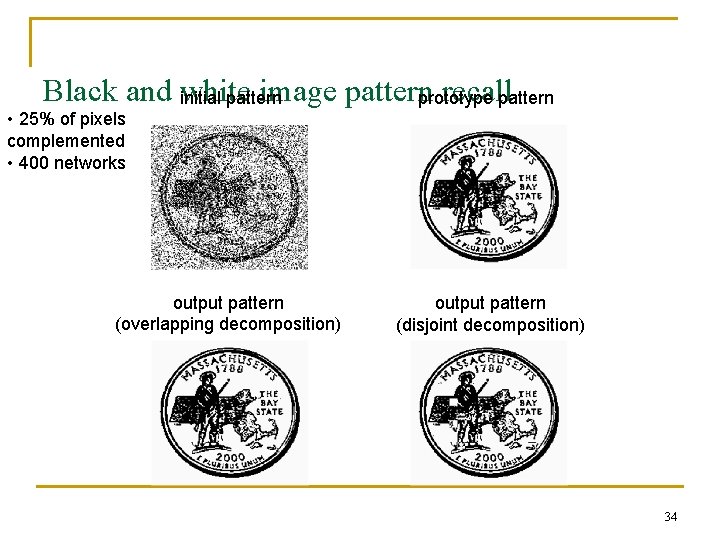
Black and white image pattern recallpattern initial pattern prototype • 25% of pixels complemented • 400 networks output pattern (overlapping decomposition) output pattern (disjoint decomposition) 34

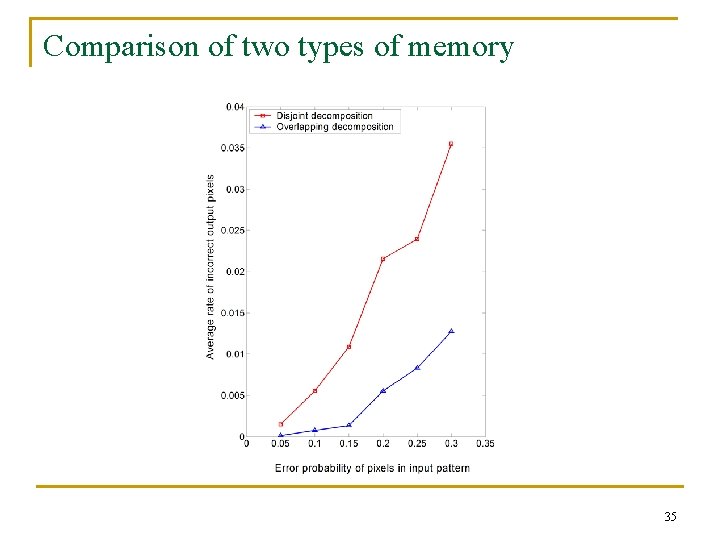
Comparison of two types of memory 35

Black and white logo patterns---150 -by-150 36

Logo recallinitial example---30% pixels complemented pattern after recall (25 networks) after error correction output pattern 37

Gray scale image patterns---150 -by-150, 6 -bit 38

Gray scale image pattern recall---100 networks, salt-and-pepper noise (40%) noisy initial image output image Salt-and-pepper noise---a 6 -bit pixel randomly selected, replaced with 0 s or 1 s 39

Color image patterns---150 -by-200, RGB 4 bit each 40

Color image pattern recall---300 networks, Gaussian noise, SD=2 noisy input image after recall (before error correction) Gaussian noise---a random number generated with Gaussian distribution added to each pixel 41

Color image pattern recall (continued) after error correction output image 42

Pattern sequence storage and retrieval with g. BSB based neural associative memory n n n Store sequences of patterns Recall the stored pattern sequence when a noisy pattern sequence is presented to the neural memory Composed of autoassociative and heteroassociative parts Autoassociative part: noise elimination/reduction → constructed with g. BSB neural network Heteroassociative part: sequencing patterns 43

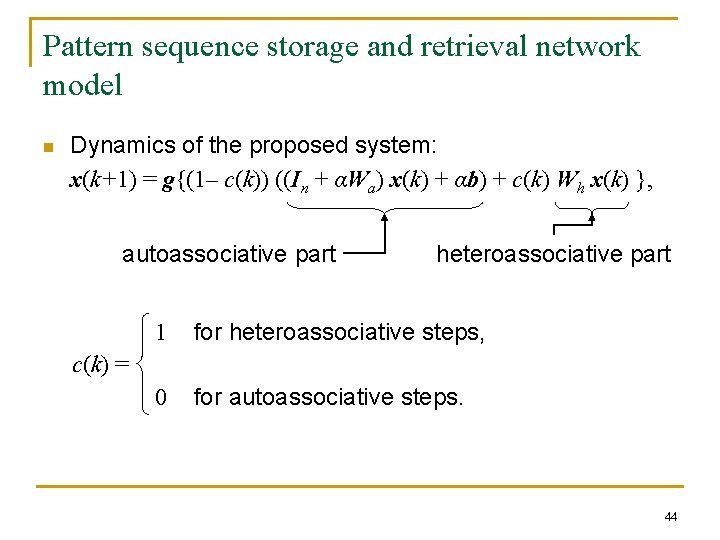
Pattern sequence storage and retrieval network model n Dynamics of the proposed system: x(k+1) = g{(1– c(k)) ((In + αWa) x(k) + αb) + c(k) Wh x(k) }, autoassociative part heteroassociative part 1 for heteroassociative steps, 0 for autoassociative steps. c(k) = 44

Model (continued) n n Construct the autoassociative part using the algorithm of Lillo et al. Construct the weight matrix of heteroassociative part: W h = V 2 V 1† where V 1 = [v 1(1) v 2(1) ··· v. L 1 -1(1) v. L 1(1) | ··· | v 1(M) v 2(M) ··· v. LM-1(M) v. LM(M) ] and V 2 = [v 2(1) v 3(1) ··· v. L 1(1) v 1(1) | ··· | v 2(M) v 3(M) ··· v. LM(M) v 1(M) ], given M pattern sequences to store v 1(1) → v 2(1) → … → v. L 1(1), … , v 1(M) → v 2(M) → … → v. LM(M) 45

Pattern Sequence Storage and Retrieval---Example (24 -by-20 bitmap images) n Prototype pattern sequences 46

Pattern Sequence Storage and Retrieval---continued (each bit complemented with 20% probability) n Snapshots of the pattern sequence recall 47

Large scale associative memory design using pattern sequence storage and retrieval n Decompose large scale patterns into small size patterns and link them to obtain pattern sequences n Store the sequences of the small size patterns in the neural associative memory that can store pattern sequences 48

Large scale associative memory design using pattern sequence storage and retrieval (continued) n When a noisy initial large scale pattern is presented to the neural associative memory, it is decomposed into a sequence of small patterns n The neural memory recalls a corresponding prototype pattern sequence n Recombine the small patterns to obtain a large scale pattern 49

Example---160 -by-200, 8 bit (48 networks, Gaussian noise, SD=30) k=0 (input) k=9 k=10 k=19 k=20 k=25 50

Example (continued) k=26 k=27 k=69 k=70 k=71 k=72 (output) 51

Summary n n Associative memories used to image pattern recall Large scale associative memory design using pattern decomposition method presented Interconnected neural associative memories proposed Novel associative memory design method using overlapping decomposition and error correction procedure presented 52

Future research n n n Develop high performance neural associative memories that can process large scale patterns in cost-effective ways Apply neural associative memories to large scale patterns such as images or three dimensional objects Use g. BSB net as basis for a neural information system to analyze and classify proteins 53

Thank You Professor Tadeusz Kaczorek, my Ph. D. advisor, 54

Thank You Professor Bartłomiej Beliczyński 55

Thank You Professor Marian P. Kaźmierkowski 56

Thank You Professor Lech Grzesiak 57

Thank You All my Friends in the Institute of Control and industrial Electronics (ISEP) 58