The General Root Locus Method adapted from ECE

The General Root Locus Method adapted from E&CE 380 - Section 8 Copyright © 1998 by William J. Wilson, University of Waterloo. All rights reserved rev. 5 of March 17, 2020 by M. Miccio see also § 15. 4 at page 290

Preliminary Definitions The general system at closed loop is: R(s) + C(s) G(s) C ( s) G ( s) R ( s ) 1 GH ( s ) – H(s) The open loop transfer function GH(s) has a transfer constant K The closed loop characteristic equation is 1+GH(s) = 0 or GH(s) = 1 defined in the set C of complex numbers and gives rise to: Magnitude criterion: GH ( s) 1 Angle criterion: GH ( s) (2 k 1) E&CE 380 k 0, 1, 2 L Frequency Response Design

Root Locus Definitions The Root Locus is the set of all points in the splane that satisfy the characteristic equation 1 + GOL(s) = 0 for any value of the transfer constant K. It is a graphical presentation of the closed-loop poles when a system parameter (e. g. , K) is varied. E&CE 380 Frequency Response Design

THE "DIRECT" ROOT LOCUS E&CE 380 Frequency Response Design

The General Root Locus Method Hypothesis 1: The TF is rational Consider a factorized polynomial (pole & zero) form of GOL(s) K ( s z 1 )( s z 2 ) …( s zm ) GH ( s ) ( s p 1 )( s p 2 ) …( s pn ) Notes: -zi zero of GOL(s) -pj pole of GOL(s) multiple root ►►► may be zero OR may be a Hypothesis 2: Hypothesis 3: m ≤ n (proper TF) K > 0 ("direct" root locus) E&CE 380 Frequency Response Design

The General Root Locus Method The previous criteria GH ( s) (2 k 1) GH ( s) 1 k 0, 1, 2 L become for a factorized polynomial (pole & zero & transfer constant) GOL(s): m GH ( s ) s z K n i i 1 s p i 1 Magnitude criterion 1 i m n i 1 GH ( s ) ( s zi ) ( s pi ) (2 k 1) Angle criterion k 0, 1, 2 L All values of s which satisfy the two criteria are roots (poles) of the closed-loop characteristic equation. E&CE 380 Frequency Response Design

Root Locus Method: Example 3 rd order K→ p 2 z 1 j X K=0 O Xp – 4 1 p 3 X E&CE 380 Frequency Response Design

Root Locus Method: Geometric Interpretation • Consider the Example No. 2 p 3 -p 3 X B s 1 K ( s z 1 ) GH ( s ) s ( s p 2 )( s p 3 ) • Then the values of s = s 1 which satisfy both: j A O -z 1 K s z 1 1 s s p 2 s p 3 C z 1 D -p 2 X X p 1 -p 1 p 2 ( s z 1 ) ( s p 2 ) ( s p 3 )) (2 k 1) are on the loci and are roots of the closed loop characteristic equation. E&CE 380 Frequency Response Design

Root Locus Method: Geometric Interpretation p 3 • In terms of the vectors, the condition for s = s 1 to be on the root loci are K A 1 or BCD j -p 3 X B s 1 A BCD K A O -z 1 and z 1 ( p 1 p 2 p 3 ) (2 k 1) k 0, 1, 2, L E&CE 380 C z 1 D -p 2 X X p 1 -p 1 p 2 Frequency Response Design

Root Locus Method • When plotting the loci of the roots as K = 0 , the magnitude condition is always satisfied. • In addition, a value of s = s 1 that satisfies the angle condition, is a point of the root loci. • The magnitude condition may then be used to determine the gain K corresponding to that value s 1. • How can we easily determine if the angle condition is satisfied? The Evans rules • They have been used for a long time as plotting guidelines to help hand sketching of root locus plots E&CE 380 Frequency Response Design

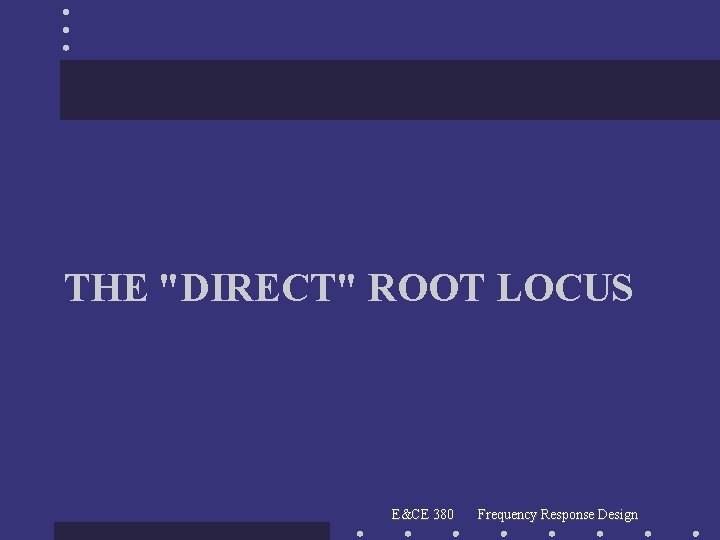
Evans’ Root Locus Construction Rules Example of 2 nd order in Matlab Example 3_DCPC_300403 pole of GOL(s) n=2 m=1 zero of GOL(s) pole of GOL(s) E&CE 380 Frequency Response Design

Evans’ Root Locus Construction Rules 1. There are n loci (as many as the system order). 2. The loci start (K = 0) at the poles of the open-loop system. The loci terminate (K ) at the zeroes of the open-loop system (include zeroes at infinity). • For our Example No. 2 s z 1 1 GH (s ) s s p 2 s p 3 K • Therefore, as K 0 , GH(s) , the poles of the loop transfer function. • As K , GH(s) 0 , the zeroes of the loop transfer function. E&CE 380 Frequency Response Design

Evans’ Root Locus Construction Rules LOCATION ON THE REAL AXIS 3. Real axis sections of the root loci exist only where there is an odd number of open-loop poles and zeroes to the right. • The roots with imaginary parts always occur in conjugate complex pairs. • When the loci approach infinity, the angles from all the poles and zeroes are equal. The angle condition then is m – n = (2 k + 1) • The angles from poles and zeroes to the left of s 1 are zero. The angles from poles and zeroes to the right are – An odd number is required to satisfy the angle criterion. E&CE 380 Frequency Response Design

Evans’ Root Locus Construction Rules ASYMPTOTES 4. As K the loci approach asymptotes. There are q = n – m asymptotes and they intersect the real axis at angles defined by k = 0, 1, 2, …, q-1 The asymptotes are equally spaced by an angle 2 /q The asymptotes intersection point (Gravity Center) on the real is given by a poles of GH (s) zeroes of GH (s) q E&CE 380 Frequency Response Design

Root Locus Construction Rules Example No. 2 j asymptotes • Consider our example with z 1 = - 4, p 1, 2 = -1 2 j, p 3 = 0 K ( s 4) GH ( s ) s ( s 1 2 j ) real axis locus O • Asymptotes: (2 k 1) angles = 3 1 2 – 4 X – 2 – 1 X 2 j X +1 – 2 j 0 (1 2 j ) ( 4) a 1 3 1 E&CE 380 Frequency Response Design

Evans’ Root Locus Construction Rules Gravity center of asymptotes in Matlab >> Gf=tf([1 1 1], [1 4 8]) >> p=pole(Gf) >> p = -2. 0000 + 2. 0000 i -2. 0000 - 2. 0000 i >> z=zero(Gf); >> cdg=((sum(p)-sum(z))/(length(p)-length(z))) cdg = -2 E&CE 380 Frequency Response Design

Evans’ Root Locus Construction Rules Asymptote angle calculation in Matlab >> Gf=tf([1 1 1], [1 4 8]) >> p=pole(Gf) >> p = -2. 0000 + 2. 0000 i -2. 0000 - 2. 0000 i >> z=zero(Gf); >> teta 1=(((2*0+1)*pi)/(length(p)-length(z)))*(180/pi) teta 1 = 36 >> teta 2=(((2*1+1)*pi)/(length(p)-length(z)))*(180/pi) teta 2 = 156. . . E&CE 380 Frequency Response Design

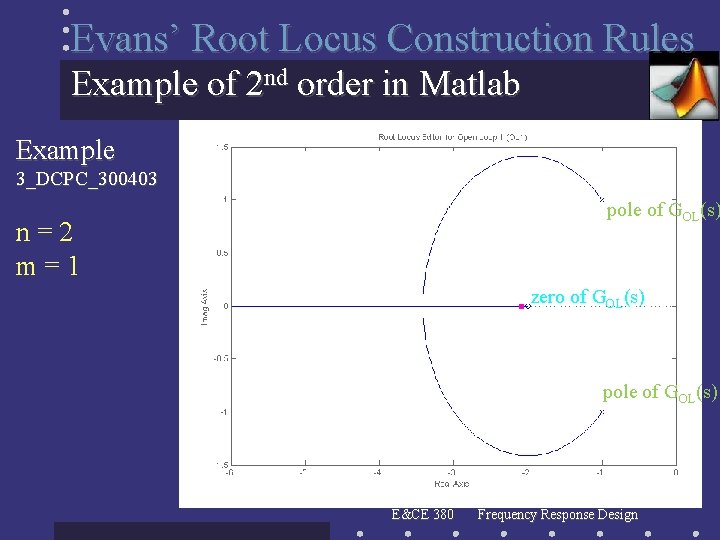
Evans’ Root Locus Construction Rules BREAKAWAY POINTS: 5. When two or more loci (an even number) meet each other, they generate a “collision” point known as a breakaway point; it corresponds to multiple roots (an even number). Some examples x x x x E&CE 380 o o 45° x x x Frequency Response Design

Root Locus Construction Rules 5 bis) The loci will breakaway from this point at particular angles calculated as 180°/k where k is the number of converging loci. 5 ter) The location of the breakaway points on the real axis is found from solving OR d. K where K = -1/GH(s) 0 ds − 2 d GH ( s ) d. K GH ( s) 0 ds ds d GH ( s ) ds d GH ( s) d N ( s) D( s) ds ds N ( s) D ( s) 0 2 D( s ) D ( s) N ( s) D ( s) 0 E&CE 380 Frequency Response Design

Root Locus Plot: Breakaway Point Example • Consider the following open loop transfer function: GH ( s) j K 2 s( s 3) 2 j • Real axis loci exist for the XX full negative axis (3 rd Evans’ rule) – 4 • Asymptotes (4 th Evans’ rule): angles = (2 k+1) = /3 , , 5 /3 3 ( 3 3 0 ) ( 0 ) a 2 3 asymptotes E&CE 380 60° – 2 X +1 – 2 j Frequency Response Design

Root Locus Plot: Breakaway Point Example • Determine the breakaway points (5 th Evans’ rule) from j 2 j d K 2 3 2 ds s ( s 3) ds s 6 s 9 s K (3 s 2 12 s 9) 0 3 2 2 ( s 6 s 9 s) – 4 then XX – 2 X +1 – 2 j s 4 s 3 ( s 1)( s 3) 0 s 1 , s 3 discarded 2 E&CE 380 Frequency Response Design

Evans’ Root Locus Construction Rules DEPARTURE / ARRIVAL ANGLES 6. The angles of departure d from an open loop pole pa of multiplicity q and arrival a to an open loop zero zb of multiplicity may be calculated from the formulas: The angles are actually obtained by applying the angle criterion to a point very near to the pole pa or the zero zb E&CE 380 Frequency Response Design

Evans’ Root Locus Construction Rules 6. bis The angles of departure from single poles and arrival to single zeroes on the real axis are always or Some examples x E&CE 380 x o Frequency Response Design o

Evans’ Root Locus Construction Rules Example No. 2: Departure Angles • Departure angle from p 2. z 1 = tan-1(2/3) = 33. 7° p 1 = tan-1(– 2/1) = 116. 6° p 3 = 90° p 2 j -p 2 X -z 1 O – 4 • Then 33. 7° – (90° + 116. 6° + p 2 ) = 180° p 2 = – 352. 9° = + 7. 1° E&CE 380 33. 7° – 2 2 j 116. 6° X -p 1 +1 90° -p. X 3 – 2 j Frequency Response Design

Evans’ Root Locus Construction Rules Angle calculation in Matlab: unit multiplicity >> Gp=tf([1 1 1], [1 4 8]); >> p=pole(Gp) >> p = % unit multiplicity -2. 0000 + 2. 0000 i -2. 0000 - 2. 0000 i Transfer function: s^2 + s + 1 ------s^2 + 4 s + 8 >> z=zero(Gp); >> teta 1=pi+sum(angle(p(1)-z))-sum(angle(p(1)-p)) teta 1 = 6. 1180 >> teta 2=pi+sum(angle(p(2)-z))-sum(angle(p(2)-p)) teta 2 = 0. 1651 >> teta 1+teta 2 % closure condition for angles of symmetric loci ans = 6. 2832 % must be equal to the "round angle" modulo 2π E&CE 380 Frequency Response Design

Root Locus Construction Rules Imaginary axis crossing The imaginary axis crossing is obtained by applying: m n a) GH(s) (s zi ) (s pi ) (2 k 1) first the angle criterion i =1 k 0, 1, 2 L for an imaginary point s* = j * m b) K s zi then the magnitude criterion to GH ( s ) n i 1 1 determine the critical gain K*, s pi i 1 i. e. , the value causing marginal stability. Reminder: Marginal stability occurs when at least one of the roots of the closedloop system is on the stability boundary, i. e. , the imaginary axis. E&CE 380 Frequency Response Design

Root Locus Construction Rules Example No. 2 Summary of results: • There are three root loci. One on the real axis from -p 1 to -z 1, and a pair of loci from -p 2 and -p 3 to zeroes at infinity along the asymptotes. • The departure angle from these poles is 7. 1° • The imaginary axis crossing is at s = 3. 16 j 7. 1° j -p 2 X -z 1 O – 4 3. 16 j 2 j X -p – 2 -p. X 3 1 +1 – 2 j – 3. 16 j The loci are symmetrical about the real axis. E&CE 380 Frequency Response Design

Root Locus Plot Example No. 3 • Open Loop Transfer Function: GH ( s ) K s ( s 4)( s 2 4 s 20) 4 j asymptotes • Roots: s = 0, s = – 4, s = – 2 4 j • Real axis segments: between 0 and – 4. • Asymptotes: (2 k 1) 3 5 7 , , , angles = 4 0 4 4 4 a ( 4 2 2 0 ) 2 4 X j 2 j 45° X – 4 4 E&CE 380 – 2 X +1 – 2 j X – 4 j Frequency Response Design

Root Locus Plot Example No. 3 • Breakaway points: points d K ds s 4 8 s 3 36 s 2 80 s K (4 s 3 24 s 2 72 s 80) 4 0 3 2 2 (s 8 s 36 s 80 s) or s 3 6 s 2 18 s 20 0 solving, sb 2, 2 2. 45 j X j 4 j 2 j 45° X – 4 – 2 X +1 – 2 j ✔ Three points breakaway at 90° X • Imaginary axis crossing: S*= 10 j 3. 16 j E&CE 380 – 4 j Frequency Response Design

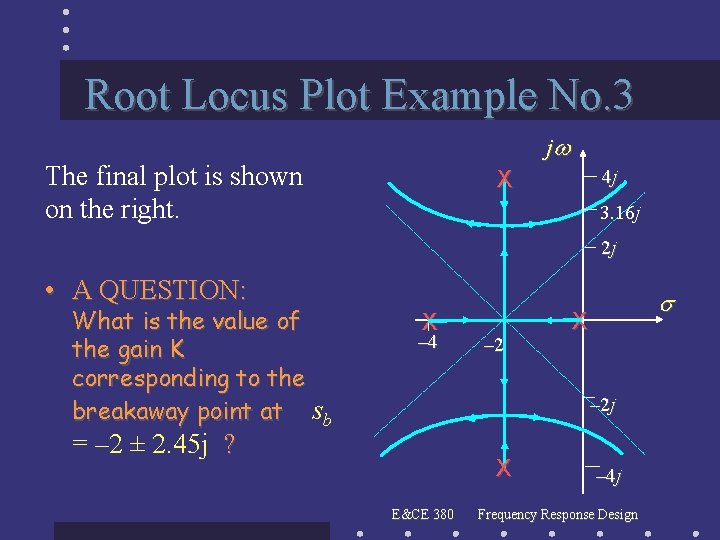
Root Locus Plot Example No. 3 j The final plot is shown on the right. X 4 j 3. 16 j 2 j • A QUESTION: What is the value of the gain K corresponding to the breakaway point at sb X – 4 – 2 X – 2 j = – 2 ± 2. 45 j ? X E&CE 380 – 4 j Frequency Response Design

Root Locus Plot Example No. 3 Gain Calculations • From the general magnitude condition n K s 1 pi i 1 m s i 1 1 zi • the gain corresponding to the point sb 1 = – 2 + 2. 45 j on the loci is K = |– 2 + 2. 45 j| ·|– 2 + 2. 45 j + 4| ·|– 2 + 2. 45 j + 2 + 4 j| ·|– 2 + 2. 45 j + 2 – 4 j| / 1. 0 = 3. 163 · 6. 45 · 1. 55 = 100 E&CE 380 Frequency Response Design

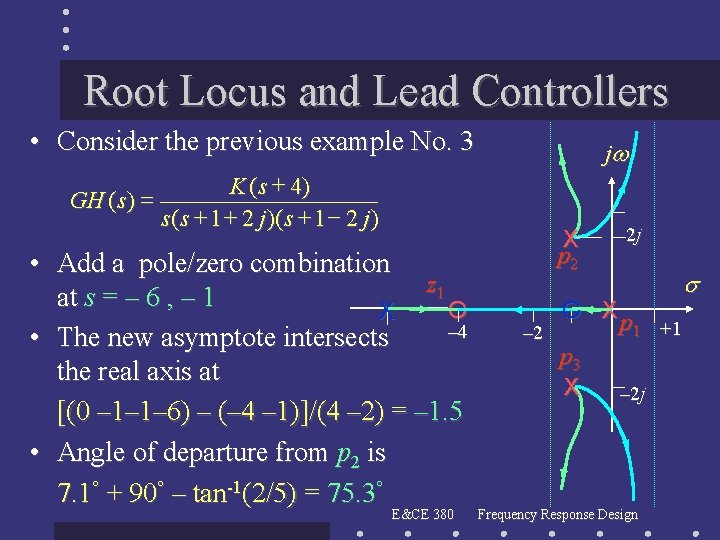
Root Locus and Lead Controllers • Consider the previous example No. 3 K ( s 4) GH ( s ) s( s 1 2 j ) • Add a pole/zero combination z 1 at s = – 6 , – 1 O X – 4 • The new asymptote intersects the real axis at [(0 – 1– 1– 6) – (– 4 – 1)]/(4 – 2) = – 1. 5 • Angle of departure from p 2 is 7. 1° + 90° – tan-1(2/5) = 75. 3° E&CE 380 j X p 2 2 j O Xp 1 +1 – 2 p 3 X – 2 j Frequency Response Design

0° ROOT LOCUS (COMPLEMENTARY OR INVERSE ROOT LOCUS) E&CE 380 Frequency Response Design

0° root locus (complementary root locus) Hypothesis 3 (changed): The loop gain K is negative in 1 + GOL(s) = 0. The characteristic equation becomes: the angle criterion changes !!! E&CE 380 Frequency Response Design

0° root locus (complementary root locus) Depending on the sign of the transfer constant k in the factorized TF form with zeroes and poles it is by definition: k > 0 "direct" root locus k < 0 0° (complementary) root locus see § 13. 2 in: Bolzern, Scattolini e Schiavoni, "Fondamenti di controlli automatici", Mc. Graw-Hill, 1998 E&CE 380 Frequency Response Design

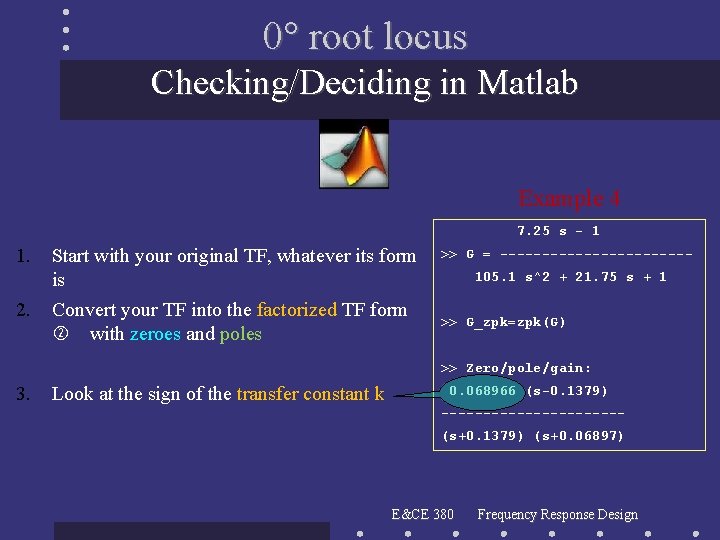
0° root locus Checking/Deciding in Matlab Example 4 7. 25 s - 1 1. 2. Start with your original TF, whatever its form is Convert your TF into the factorized TF form with zeroes and poles >> G = -----------105. 1 s^2 + 21. 75 s + 1 >> G_zpk=zpk(G) >> Zero/pole/gain: 3. Look at the sign of the transfer constant k 0. 068966 (s-0. 1379) -----------(s+0. 1379) (s+0. 06897) E&CE 380 Frequency Response Design

0° root locus (complementary root locus) RULE 3 changes ! 3. Real axis sections of the root loci exist only where there is an even number of poles and zeroes to the right. RULES involving angle calculation change ! (2 k + 1) (2 k) E&CE 380 Frequency Response Design

0° root locus (complementary root locus) Angle criterion 4. ASYMPTOTES As K the loci approach asymptotes. There are q = n – m asymptotes and they intersect the real axis at angles defined by E&CE 380 Frequency Response Design

0° root locus (complementary root locus) 6. The angles of departure, d from a pole pa and arrival, a to zero zb may be calculated from E&CE 380 Frequency Response Design

CONCLUSIONS E&CE 380 Frequency Response Design

Root Locus Usage • The Root Locus method cannot work with TFs containing a transcendent term • The roots of the closed-loop characteristic equation 1 + GOL(s) = 0 define the stability of the system time-domain responses • The Root Loci are symmetrical about the real axis • While the poles of a closed-loop system are very important in determining its BIBO stability, the zeroes of the system can also play a role in the dynamic response • With MATLAB, our need for the Evans rules is minimal! (from P. C. Chau, “Process Control: A First Course with MATLAB”) E&CE 380 Frequency Response Design

Root Locus Analysis • The Root Locus is a powerful method of analysis and design for closed loop stability • The loop gain K mostly brings into account the role of the controller gain Kc • The Root Locus provides the engineer with a measure of the sensitivity of the closed loop system (through its poles) to a variation in any parameter being considered for the dynamic system • The closed loop pole location leads to prediction of the characteristics of the time domain responses in terms of: – – – time constant, first-order modes damping ratio, second-order modes natural frequency, n E&CE 380 Frequency Response Design

Root Locus Plotter (didactical trial-and-error method) Example: p 1 = +3 j p 2 = -3 j z 1= -2 z 2= -4 Click here for Interactive Shockwave Animation http: //www. wiley. com/college/nise/0471794759/swf/Q 8 -02 -C. swf Norman S. Nise, Control Systems Engineering, 5 th Edition, California State Polytechnic University E&CE 380 Frequency Response Design

APPENDIX E&CE 380 Frequency Response Design

Root Locus: Example No. 1 R(s) E(s) + – C(s) K s ( s 2) The open-loop transfer function is The closed-loop characteristic equation becomes: GOL(s)=K/[s(s+2)] C (s) K R( s) s( s 2) K s 2 2 s K 0 Consider the closed-loop poles as K 0 E&CE 380 Frequency Response Design

Root Locus: Example No. 1 s 1 1 K • For K = 0 the closed-loop poles are at the open-loop poles. • For 0 K 1 the closed-loop poles are on the real axis. • For K 1 the closed-loop poles are complex, with a real value of – 1 and an imaginary value increasing with gain K. loci of closed-loop roots E&CE 380 j K K=1 X – 2 X K=0 Frequency Response Design

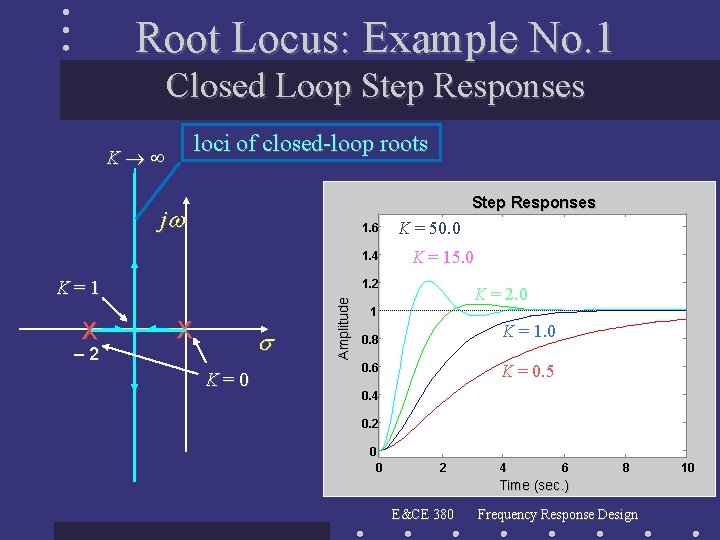
Root Locus: Example No. 1 Closed Loop Step Responses loci of closed-loop roots K Step Responses j 1. 6 1. 4 K=1 – 2 K = 15. 0 1. 2 X K=0 Amplitude X K = 50. 0 K = 2. 0 1 K = 1. 0 0. 8 K = 0. 5 0. 6 0. 4 0. 2 0 0 2 4 6 8 Time (sec. ) E&CE 380 Frequency Response Design 10

Root Locus: Example No. 1 Some Observations • • • This is a second-order system and there two loci. The root loci start at the open-loop poles. The root loci tend towards infinity as K . (Note: infinitely large values can be regarded open loop zeroes. ) • The relationship between the time-domain responses and the increasing gain is seen through the root loci. E&CE 380 Frequency Response Design