The General Linear Model Guillaume Flandin Wellcome Trust

The General Linear Model Guillaume Flandin Wellcome Trust Centre for Neuroimaging University College London SPM Short Course London, 20 -22 Oct 2011

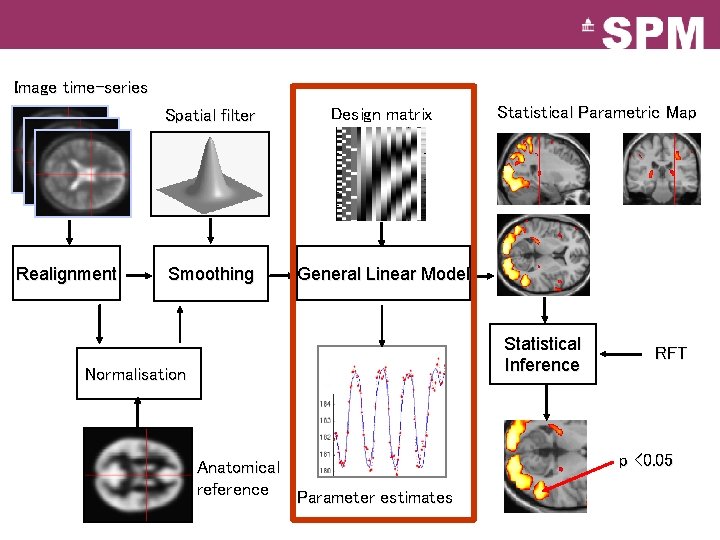
Image time-series Realignment Spatial filter Design matrix Smoothing General Linear Model Statistical Parametric Map Statistical Inference Normalisation Anatomical reference Parameter estimates RFT p <0. 05

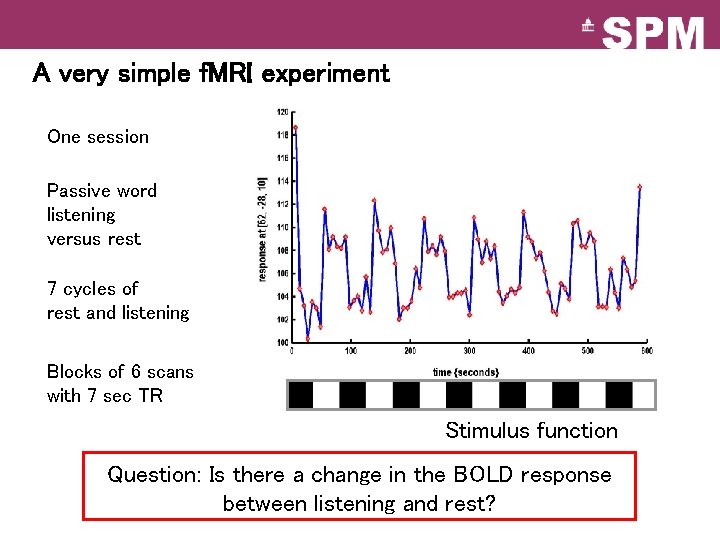
A very simple f. MRI experiment One session Passive word listening versus rest 7 cycles of rest and listening Blocks of 6 scans with 7 sec TR Stimulus function Question: Is there a change in the BOLD response between listening and rest?

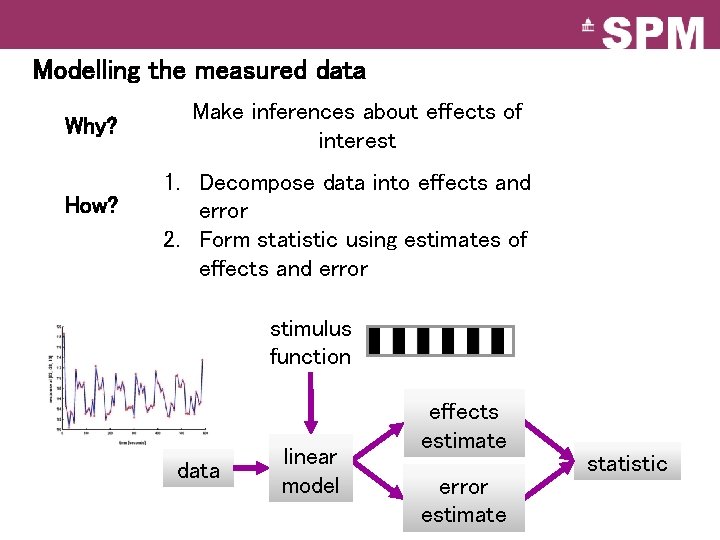
Modelling the measured data Why? How? Make inferences about effects of interest 1. Decompose data into effects and error 2. Form statistic using estimates of effects and error stimulus function data linear model effects estimate error estimate statistic

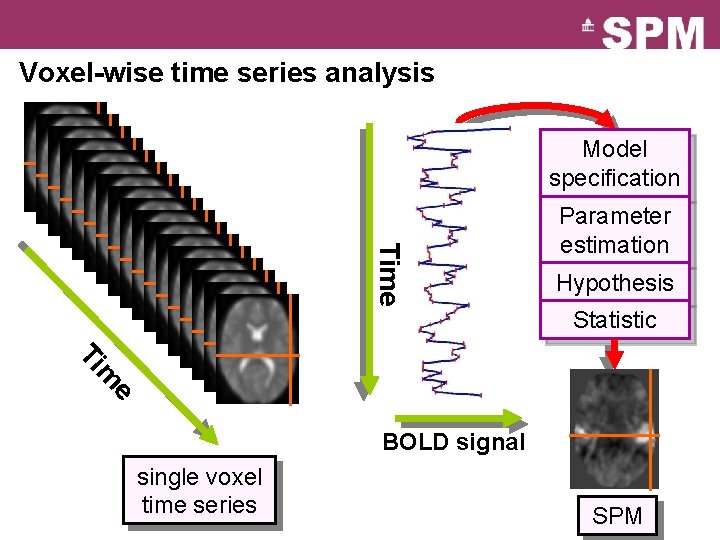
Voxel-wise time series analysis Model specification Time Parameter estimation Hypothesis Statistic e m Ti BOLD signal single voxel time series SPM

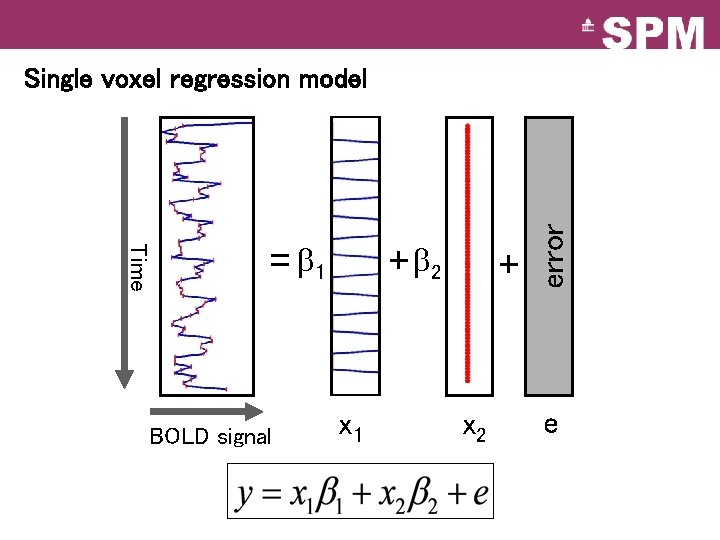
Time = 1 BOLD signal + 2 x 1 + x 2 error Single voxel regression model e

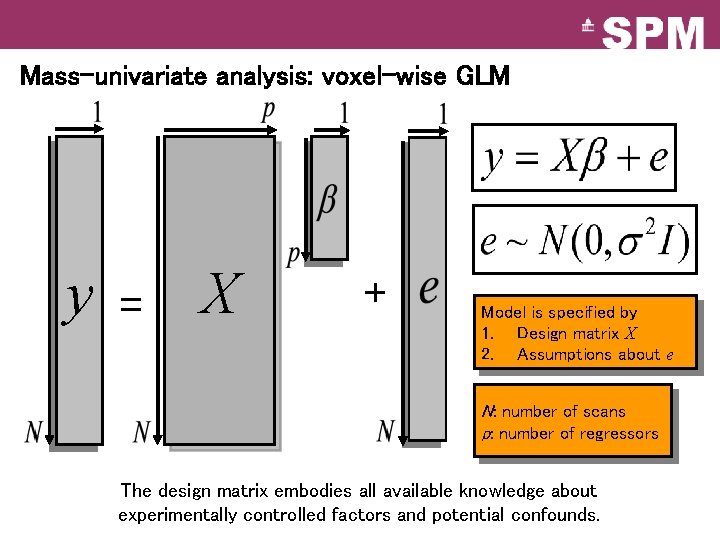
Mass-univariate analysis: voxel-wise GLM y = X + Model is specified by 1. Design matrix X 2. Assumptions about e N: number of scans p: number of regressors The design matrix embodies all available knowledge about experimentally controlled factors and potential confounds.

GLM: mass-univariate parametric analysis • • • one sample t-test two sample t-test paired t-test Analysis of Variance (ANOVA) Factorial designs correlation linear regression multiple regression F-tests f. MRI time series models Etc. .

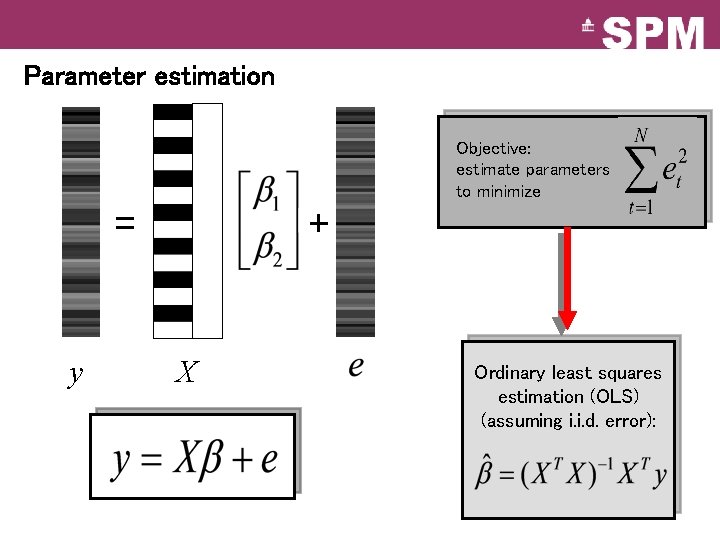
Parameter estimation Objective: estimate parameters to minimize = y + X Ordinary least squares estimation (OLS) (assuming i. i. d. error):

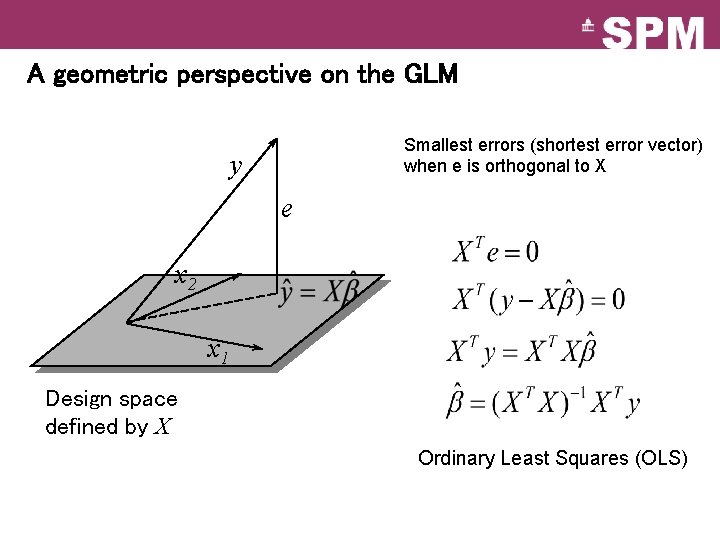
A geometric perspective on the GLM Smallest errors (shortest error vector) when e is orthogonal to X y e x 2 x 1 Design space defined by X Ordinary Least Squares (OLS)

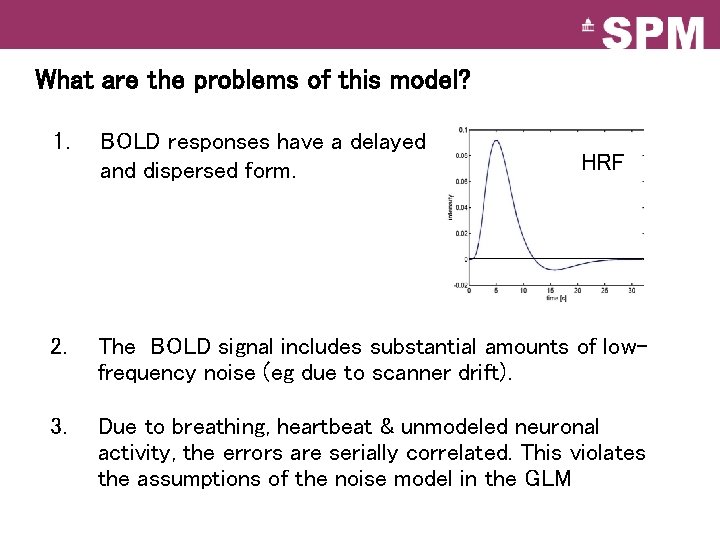
What are the problems of this model? 1. BOLD responses have a delayed and dispersed form. 2. The BOLD signal includes substantial amounts of lowfrequency noise (eg due to scanner drift). 3. Due to breathing, heartbeat & unmodeled neuronal activity, the errors are serially correlated. This violates the assumptions of the noise model in the GLM HRF

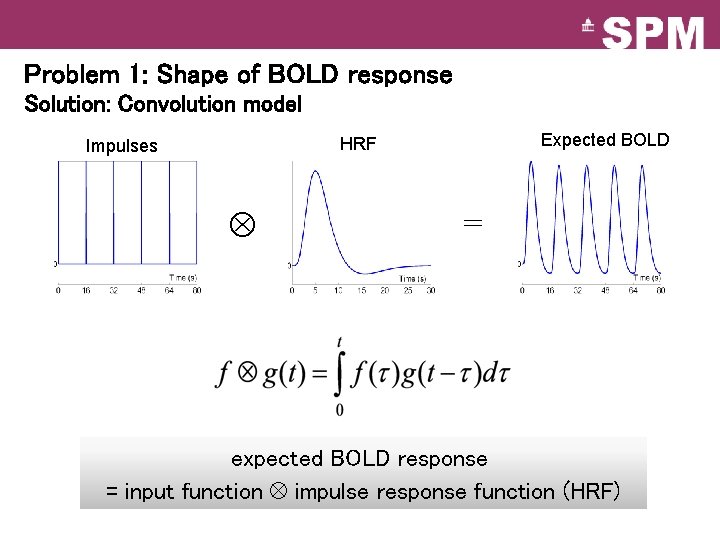
Problem 1: Shape of BOLD response Solution: Convolution model Expected BOLD HRF Impulses = expected BOLD response = input function impulse response function (HRF)

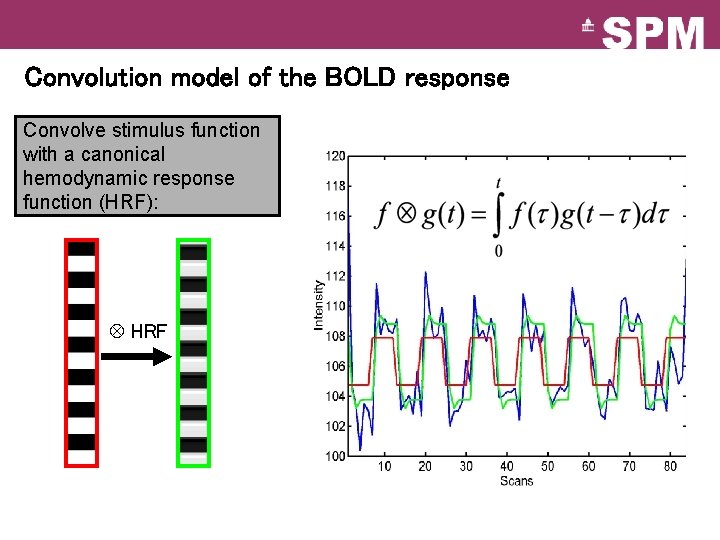
Convolution model of the BOLD response Convolve stimulus function with a canonical hemodynamic response function (HRF): HRF

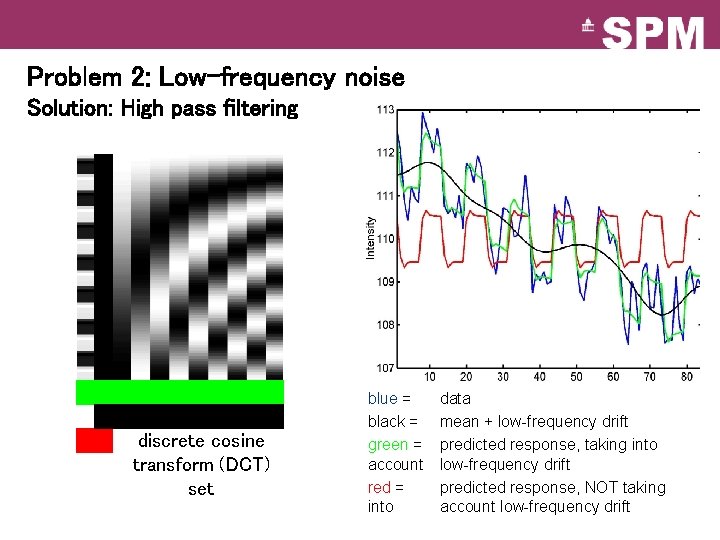
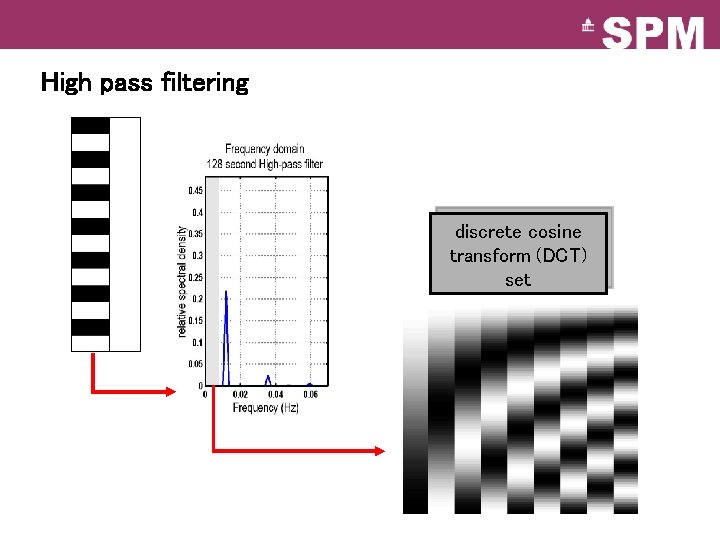
Problem 2: Low-frequency noise Solution: High pass filtering discrete cosine transform (DCT) set blue = black = green = account red = into data mean + low-frequency drift predicted response, taking into low-frequency drift predicted response, NOT taking account low-frequency drift

High pass filtering discrete cosine transform (DCT) set

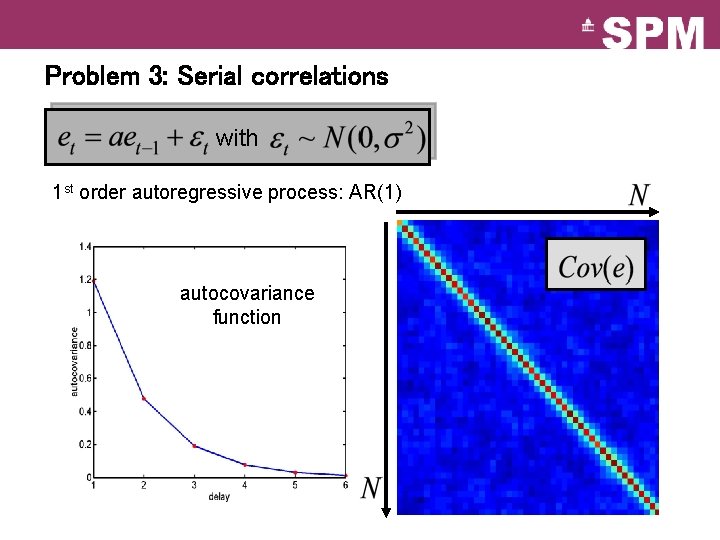
Problem 3: Serial correlations with 1 st order autoregressive process: AR(1) autocovariance function

Multiple covariance components enhanced noise model at voxel i V = 1 error covariance components Q and hyperparameters Q 1 + 2 Q 2 Estimation of hyperparameters with Re. ML (Restricted Maximum Likelihood).

Parameters can then be estimated using Weighted Least Squares (WLS) Let Then where WLS equivalent to OLS on whitened data and design

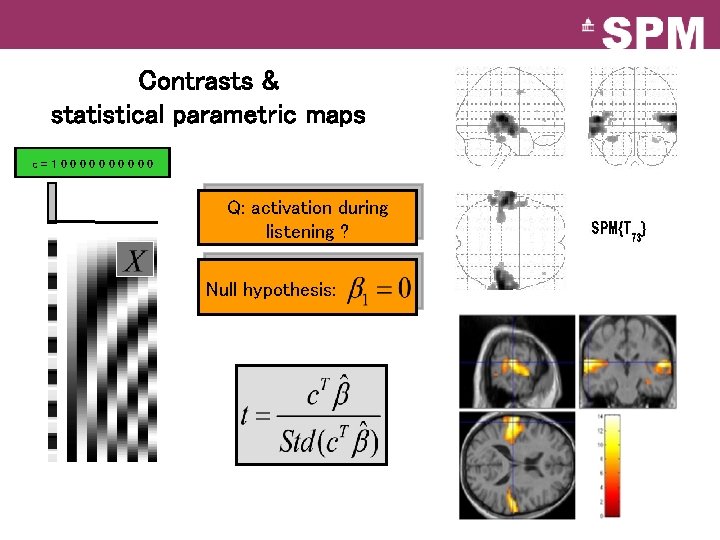
Contrasts & statistical parametric maps c=100000 Q: activation during listening ? Null hypothesis:

Summary q Mass univariate approach. q Fit GLMs with design matrix, X, to data at different points in space to estimate local effect sizes, q GLM is a very general approach q Hemodynamic Response Function q High pass filtering q Temporal autocorrelation