THE GENERAL EQUATION OF A STRAIGHT LINE y

THE GENERAL EQUATION OF A STRAIGHT LINE

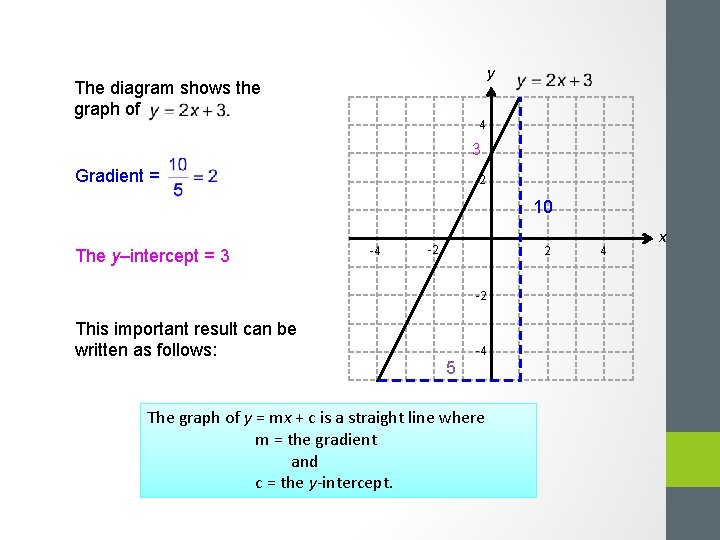
y The diagram shows the graph of 4 3 Gradient = 2 10 The y–intercept = 3 -4 -2 2 -2 This important result can be written as follows: -4 5 The graph of y = mx + c is a straight line where m = the gradient and c = the y-intercept. 4 x

Examples 1 Find the gradient and y-intercept for the line gradient = 3 y-intercept = − 4

2 Find the gradient and y-intercept for the line gradient = − 2 y-intercept = 6

2 A line is parallel to the line and passes through the point (5, 1). Find the equation of the line. Parallel lines have the same gradient. The equation of the parallel line is The line passes through the point (5, 1) so substitute x = 5 and y = 1 into the equation. The equation is:

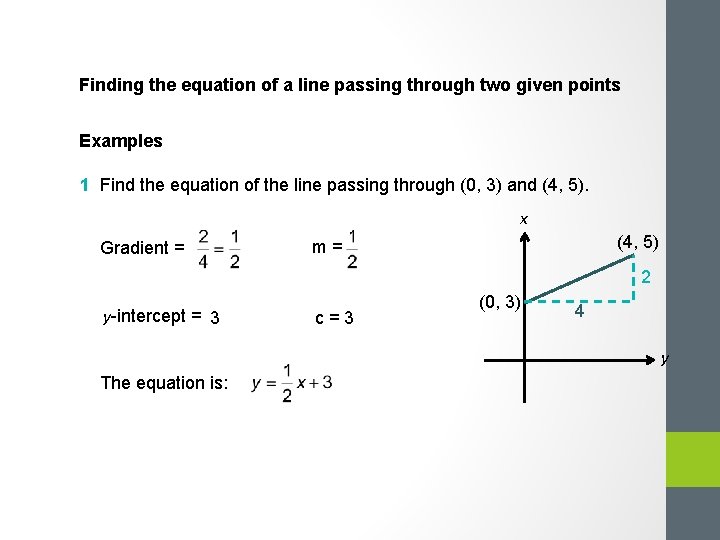
Finding the equation of a line passing through two given points Examples 1 Find the equation of the line passing through (0, 3) and (4, 5). x Gradient = (4, 5) m= 2 y-intercept = 3 c=3 (0, 3) 4 y The equation is:

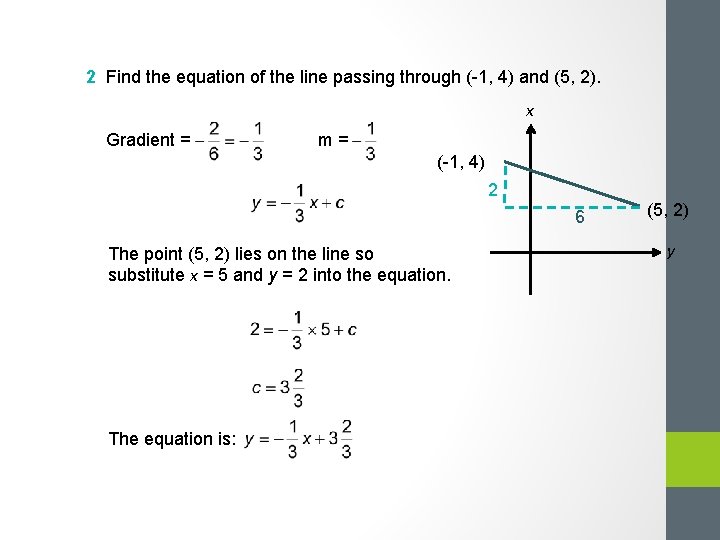
2 Find the equation of the line passing through (-1, 4) and (5, 2). x Gradient = m= (-1, 4) 2 6 The point (5, 2) lies on the line so substitute x = 5 and y = 2 into the equation. The equation is: (5, 2) y

Finding the midpoint of a line The midpoint of a line segment can be found using a diagram or by using the following rule: Midpoint = (mean of the x coordinates, mean of the y coordinates) Examples 1 Find the midpoint of the line joining the points (1, 6) and (9, 2). Mean of x coordinates = Mean of y coordinates = Midpoint = (5, 4)

2 Find the midpoint of the line joining the points (-2, 4) and (6, 2). Mean of x coordinates = Mean of y coordinates = Midpoint = (2, 3) 3 Find the midpoint of the line joining the points (3, -5) and (-9, -7). Mean of x coordinates = Mean of y coordinates = Midpoint = (-3, -6)